鲁教版2024-2025学年度第一学期九年级数学2.4 解直角三角形 同步练习(含答案)
文档属性
| 名称 | 鲁教版2024-2025学年度第一学期九年级数学2.4 解直角三角形 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 363.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-12 19:02:02 | ||
图片预览



文档简介
鲁教版2024-2025学年度第一学期九年级数学2.4 解直角三角形 同步练习
班级: 姓名:
亲爱的同学们:
练习开始了,希望你认真审题,细致做题,运用所学知识解决本练习。祝你学习进步!
一、单选题
1.在Rt△ABC中,∠C=90°,∠B=α,若BC=m,则AB的长为( )
A. B.m cosα C.m sinα D.m tanα
2.在 中, , ,则 ( )
A. B. C. D.
3.如图是冬奥会首钢滑雪大跳台赛道的剖面图,剖面图的一部分可抽象为线段,已知坡长为m米,坡角为α,则坡的铅垂高度为( )
A.米 B.米 C.米 D.米
4.已知,在△ABC中,∠A∶∠B∶∠C=1∶2∶3,BC=a,AC=b,AB=c,则下列结论错误的是( )
A.c= b B.c=2a C.b2=3a2 D.a2+b2=c2
5.在Rt△ACB中,∠C=90°,AB=10,sinA= ,则BC的长为( )
A.6 B.7.5 C.8 D.12.5
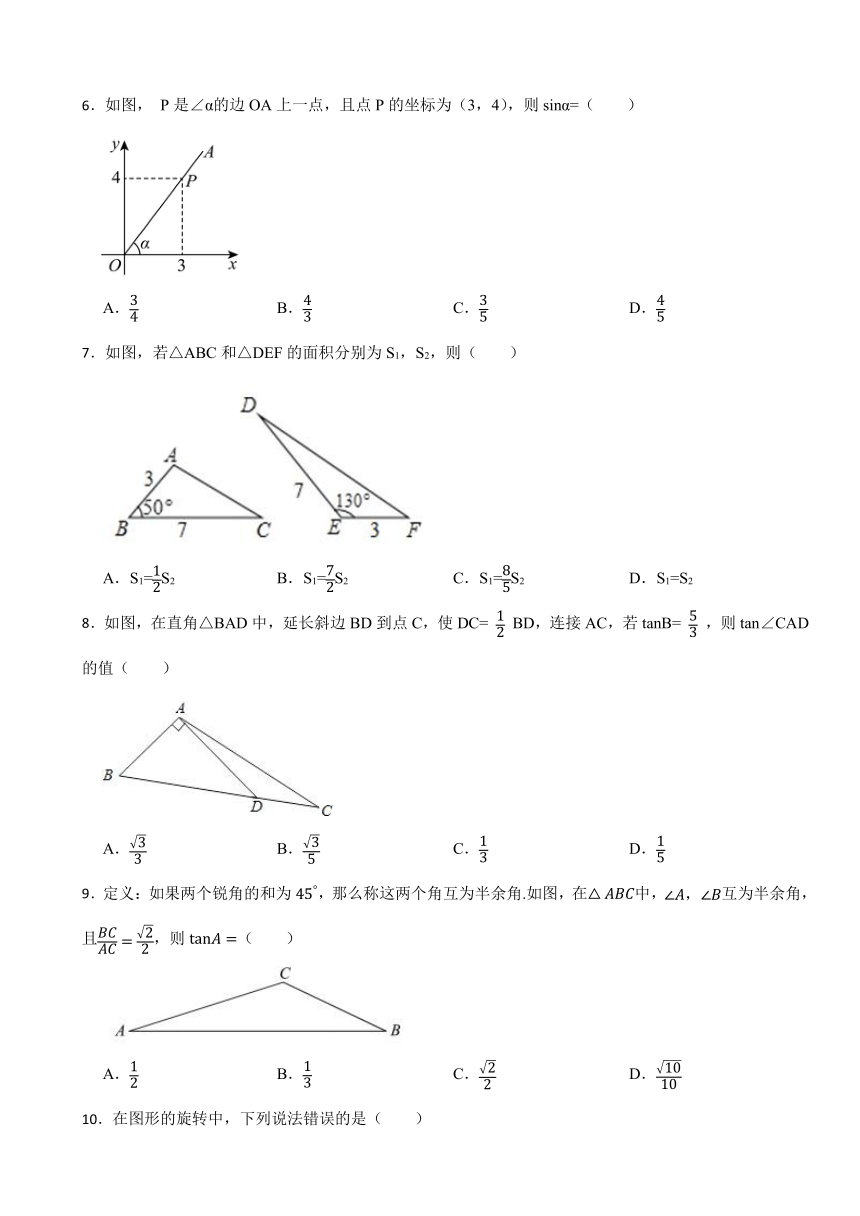
6.如图, P是∠α的边OA上一点,且点P的坐标为(3,4),则sinα=( )
A. B. C. D.
7.如图,若△ABC和△DEF的面积分别为S1,S2,则( )
A.S1=S2 B.S1=S2 C.S1=S2 D.S1=S2
8.如图,在直角△BAD中,延长斜边BD到点C,使DC= BD,连接AC,若tanB= ,则tan∠CAD的值( )
A. B. C. D.
9.定义:如果两个锐角的和为,那么称这两个角互为半余角.如图,在中,互为半余角,且,则( )
A. B. C. D.
10.在图形的旋转中,下列说法错误的是( )
A.旋转前和旋转后的图形全等
B.图形上的每一个点到旋转中心的距离都相等
C.图形上的每一个点旋转的角度都相同
D.图形上可能存在不动的点
二、填空题
11.如果△+△=*,○+○=,△=○+○+○+○,那么*+= .
12.已知α是锐角,且sinα= ,则cosα= .
13.在 中, , , , .
14.如图,在中,,,,,为的中点,点、分别为、上一动点,则的最小值为 .
15.在△ABC中,AC=6 ,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为 ,并且CD⊥AC,则BC的长为 .
三、解答题
16.如图,点P是 外一点,点M、N分别是 两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若 , , ,则线段QR的长为多少 .
17.如图,在Rt△ABC中,∠C=90°,tanA= ,BC=12,求AB的长.
18.在△ABC中,sinB= ,AB=15,∠C=45°,求△ABC的周长(结果保留根号).
19.如图,在△ABC中,∠C=90°,sinB= ,AB=15,求△ABC的周长和tanA的值.
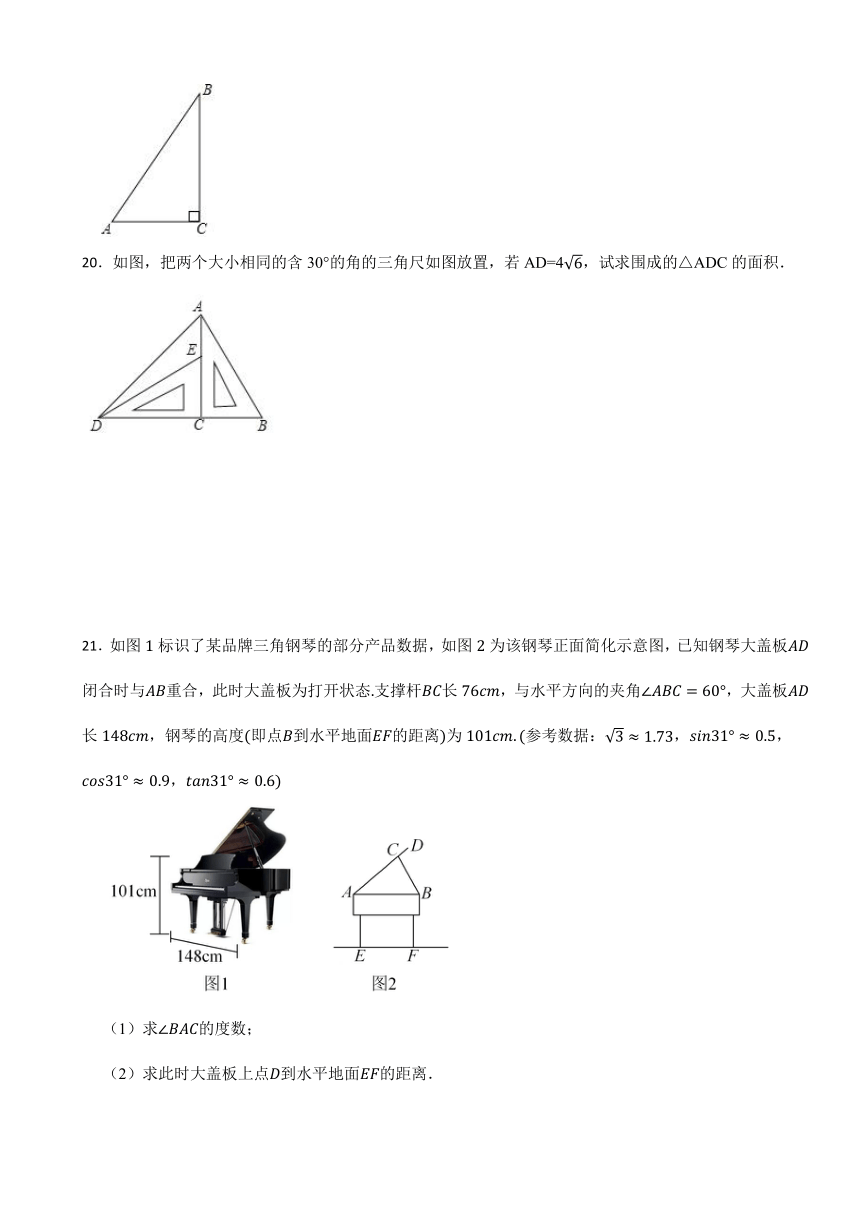
20.如图,把两个大小相同的含30°的角的三角尺如图放置,若AD=4,试求围成的△ADC的面积.
21.如图标识了某品牌三角钢琴的部分产品数据,如图为该钢琴正面简化示意图,已知钢琴大盖板闭合时与重合,此时大盖板为打开状态支撑杆长,与水平方向的夹角,大盖板长,钢琴的高度即点到水平地面的距离为参考数据:,,,
(1)求的度数;
(2)求此时大盖板上点到水平地面的距离.
22.如图,在梯形ABCD中,∠A=∠B=90°,AB=,点E在AB上,∠AED=45°,DE=6,CE=7.
(1)求AE的长;
(2)求sin∠BCE的值.
23.如图是小强洗漱时的侧面示意图,洗漱台(矩形 )靠墙摆放,高 ,宽 ,小强身高 ,下半身 ,洗漱时下半身与地面成 ( ),身体前倾成 ( ),脚与洗漱台距离 (点 , , , 在同一直线上).
(1)此时小强头部 点与地面 相距多少?
(2)小强希望他的头部 恰好在洗漱盆 的中点 的正上方,他应向前或后退多少?
( , , ,结果精确到 )
24.如图,矩形ABCD的对角线AC、BD相交于点O,过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值.
1.A
2.C
3.B
4.A
5.A
6.D
7.D
8.D
9.B
10.B
11.10○
12.
13.8
14.
15. 或15
16.解: ,理由如下:
点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上,
, .
, , ,
, , .
.
17.解:∵∠C=90°,BC=12,tanA= = ,
∴AC=16,
∵AB2=AC2+BC2,
∴AB2=162+122=400,
∴AB=20.
18.解:作AD⊥BC于D,如图所示:
∵sinB= = ,AB=15,
∴AD= AB= ×15=9,
∴BD= = =12,
∵∠C=45°,
∴△ACD是等腰直角三角形,
∴CD=AD=9,
∴BC=BD+CD=21,AC= AD=9 ,
∴△ABC的周长=AB+BC+AC=15+21+9 =36+9 .
19.解:在△ABC中,因为∠C=90°, ,AB=15,
所以 = ,即 = ,
所以AC=9,
又因为AC2+BC2=AB2,
所以BC=12,
所以△ABC的周长AC+BC+AB=9+12+15=36,
20.解:∵由图知,AC=CD,∠ACD=90°,
∴△ACD为等腰直角三角形,
∴∠ADC=45°.
∴AC=ADsin45°=4×=4,
△ADC的面积:DC AC=×4×4=24.
21.(1)解:过点作,垂足为,
由题意得:,
在中,,,
,
,
,
在中,,
,
的度数约为;
(2)解:过点作,垂足为,
在中,,,
,
点到水平地面的距离为,
此时大盖板上点到水平地面的距离,
此时大盖板上点到水平地面的距离约为.
22.(1)在中,,,
∵
∴==;
(2)∵
∴
在中,,=.
23.(1)解:过点F作FN⊥DK于点N,过点E作EM⊥FN于点M,
∵EF+FG=166,FG=100,∴EF=66,
∵∠FGK=80°,∴FN=100sin80°≈98,
又∵∠EFG=125°,∴∠EFM=180°-125°-10°=45°,
∴FM=66cos45°=33≈46.53,
∴MN=FN+FM≈144.5.
∴他头部E点与地面DK相距约144.5cm。
(2)解:过点E作EP⊥AB于点P,延长OB交MN于点H。
∵AB=48,O为AB的中点,
∴AO=BO=24,
∵EM=66sin45°≈46.53,即PH≈46.53
GN=100cos80°≈1,8,CG=15,
∴OH=24+15+18==57
OP=OH-PH=57-46.53=10.47≈10.5,
∴他应向前10.5cm。
24.解:连接EC,∵四边形ABCD为矩形,∴OA=OC,∠ABC=90°,利用勾股定理得:AC==10,即OA=5,∵OE⊥AC,∴AE=CE,在Rt△EDC中,设EC=AE=x,则有ED=AD﹣AE=8﹣x,DC=AB=6,根据勾股定理得:x2=(8﹣x)2+62,解得:x=,∴AE=,在Rt△AOE中,sin∠OEA==.
班级: 姓名:
亲爱的同学们:
练习开始了,希望你认真审题,细致做题,运用所学知识解决本练习。祝你学习进步!
一、单选题
1.在Rt△ABC中,∠C=90°,∠B=α,若BC=m,则AB的长为( )
A. B.m cosα C.m sinα D.m tanα
2.在 中, , ,则 ( )
A. B. C. D.
3.如图是冬奥会首钢滑雪大跳台赛道的剖面图,剖面图的一部分可抽象为线段,已知坡长为m米,坡角为α,则坡的铅垂高度为( )
A.米 B.米 C.米 D.米
4.已知,在△ABC中,∠A∶∠B∶∠C=1∶2∶3,BC=a,AC=b,AB=c,则下列结论错误的是( )
A.c= b B.c=2a C.b2=3a2 D.a2+b2=c2
5.在Rt△ACB中,∠C=90°,AB=10,sinA= ,则BC的长为( )
A.6 B.7.5 C.8 D.12.5
6.如图, P是∠α的边OA上一点,且点P的坐标为(3,4),则sinα=( )
A. B. C. D.
7.如图,若△ABC和△DEF的面积分别为S1,S2,则( )
A.S1=S2 B.S1=S2 C.S1=S2 D.S1=S2
8.如图,在直角△BAD中,延长斜边BD到点C,使DC= BD,连接AC,若tanB= ,则tan∠CAD的值( )
A. B. C. D.
9.定义:如果两个锐角的和为,那么称这两个角互为半余角.如图,在中,互为半余角,且,则( )
A. B. C. D.
10.在图形的旋转中,下列说法错误的是( )
A.旋转前和旋转后的图形全等
B.图形上的每一个点到旋转中心的距离都相等
C.图形上的每一个点旋转的角度都相同
D.图形上可能存在不动的点
二、填空题
11.如果△+△=*,○+○=,△=○+○+○+○,那么*+= .
12.已知α是锐角,且sinα= ,则cosα= .
13.在 中, , , , .
14.如图,在中,,,,,为的中点,点、分别为、上一动点,则的最小值为 .
15.在△ABC中,AC=6 ,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为 ,并且CD⊥AC,则BC的长为 .
三、解答题
16.如图,点P是 外一点,点M、N分别是 两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在线段MN的延长线上.若 , , ,则线段QR的长为多少 .
17.如图,在Rt△ABC中,∠C=90°,tanA= ,BC=12,求AB的长.
18.在△ABC中,sinB= ,AB=15,∠C=45°,求△ABC的周长(结果保留根号).
19.如图,在△ABC中,∠C=90°,sinB= ,AB=15,求△ABC的周长和tanA的值.
20.如图,把两个大小相同的含30°的角的三角尺如图放置,若AD=4,试求围成的△ADC的面积.
21.如图标识了某品牌三角钢琴的部分产品数据,如图为该钢琴正面简化示意图,已知钢琴大盖板闭合时与重合,此时大盖板为打开状态支撑杆长,与水平方向的夹角,大盖板长,钢琴的高度即点到水平地面的距离为参考数据:,,,
(1)求的度数;
(2)求此时大盖板上点到水平地面的距离.
22.如图,在梯形ABCD中,∠A=∠B=90°,AB=,点E在AB上,∠AED=45°,DE=6,CE=7.
(1)求AE的长;
(2)求sin∠BCE的值.
23.如图是小强洗漱时的侧面示意图,洗漱台(矩形 )靠墙摆放,高 ,宽 ,小强身高 ,下半身 ,洗漱时下半身与地面成 ( ),身体前倾成 ( ),脚与洗漱台距离 (点 , , , 在同一直线上).
(1)此时小强头部 点与地面 相距多少?
(2)小强希望他的头部 恰好在洗漱盆 的中点 的正上方,他应向前或后退多少?
( , , ,结果精确到 )
24.如图,矩形ABCD的对角线AC、BD相交于点O,过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值.
1.A
2.C
3.B
4.A
5.A
6.D
7.D
8.D
9.B
10.B
11.10○
12.
13.8
14.
15. 或15
16.解: ,理由如下:
点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上,
, .
, , ,
, , .
.
17.解:∵∠C=90°,BC=12,tanA= = ,
∴AC=16,
∵AB2=AC2+BC2,
∴AB2=162+122=400,
∴AB=20.
18.解:作AD⊥BC于D,如图所示:
∵sinB= = ,AB=15,
∴AD= AB= ×15=9,
∴BD= = =12,
∵∠C=45°,
∴△ACD是等腰直角三角形,
∴CD=AD=9,
∴BC=BD+CD=21,AC= AD=9 ,
∴△ABC的周长=AB+BC+AC=15+21+9 =36+9 .
19.解:在△ABC中,因为∠C=90°, ,AB=15,
所以 = ,即 = ,
所以AC=9,
又因为AC2+BC2=AB2,
所以BC=12,
所以△ABC的周长AC+BC+AB=9+12+15=36,
20.解:∵由图知,AC=CD,∠ACD=90°,
∴△ACD为等腰直角三角形,
∴∠ADC=45°.
∴AC=ADsin45°=4×=4,
△ADC的面积:DC AC=×4×4=24.
21.(1)解:过点作,垂足为,
由题意得:,
在中,,,
,
,
,
在中,,
,
的度数约为;
(2)解:过点作,垂足为,
在中,,,
,
点到水平地面的距离为,
此时大盖板上点到水平地面的距离,
此时大盖板上点到水平地面的距离约为.
22.(1)在中,,,
∵
∴==;
(2)∵
∴
在中,,=.
23.(1)解:过点F作FN⊥DK于点N,过点E作EM⊥FN于点M,
∵EF+FG=166,FG=100,∴EF=66,
∵∠FGK=80°,∴FN=100sin80°≈98,
又∵∠EFG=125°,∴∠EFM=180°-125°-10°=45°,
∴FM=66cos45°=33≈46.53,
∴MN=FN+FM≈144.5.
∴他头部E点与地面DK相距约144.5cm。
(2)解:过点E作EP⊥AB于点P,延长OB交MN于点H。
∵AB=48,O为AB的中点,
∴AO=BO=24,
∵EM=66sin45°≈46.53,即PH≈46.53
GN=100cos80°≈1,8,CG=15,
∴OH=24+15+18==57
OP=OH-PH=57-46.53=10.47≈10.5,
∴他应向前10.5cm。
24.解:连接EC,∵四边形ABCD为矩形,∴OA=OC,∠ABC=90°,利用勾股定理得:AC==10,即OA=5,∵OE⊥AC,∴AE=CE,在Rt△EDC中,设EC=AE=x,则有ED=AD﹣AE=8﹣x,DC=AB=6,根据勾股定理得:x2=(8﹣x)2+62,解得:x=,∴AE=,在Rt△AOE中,sin∠OEA==.
