鲁教版2024-2025学年度第一学期九年级上册数学 第一章 反比例函数 单元测试(含答案)
文档属性
| 名称 | 鲁教版2024-2025学年度第一学期九年级上册数学 第一章 反比例函数 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-12 00:00:00 | ||
图片预览




文档简介
鲁教版2024-2025学年度第一学期九年级数学第一章 反比例函数 单元测试
班级: 姓名:
亲爱的同学们:
练习开始了,希望你认真审题,细致做题,运用所学知识解决本练习。祝你学习进步!
一、单选题
1.下列函数关系式中属于反比例函数的是( )
A. B. C. D.
2.若反比例函数的图象经过点,则图象必经过点( )
A. B. C. D.
3.如图,点P在反比例函数y= (x>0)的图象上,且横坐标为2.若将点P先向右平移两个单位,再向上平移一个单位后所得的点为点P′.则在第一象限内,经过点P′的反比例函数图象的解析式是( )
A.y=- (x>0) B.y= (x>0)
C.y=- (x>0) D.y= (x>0)
4.已知点,在函数的图象上,当且时,都有,则的取值范围为( )
A. B. C. D.
5.若点(x1,y1)、(x2,y2)和(x3,y3)分别在反比例函数 的图象上,且 ,则下列判断中正确的是( )
A. B. C. D.
6.若点是反比例函数图象上一点,则常数的值为( )
A.3 B. C. D.
7.如图所示,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数和的图象交于点A和点B,若点C是x轴上任意一点,连接,则的面积为( )
A.6 B.7 C.8 D.14
8.根据欧姆定律可知,若一个灯泡的电压保持不变,通过灯泡的电流越大,则灯泡就越亮当电阻时,可测得某灯泡的电流若电压保持不变,电阻减小为时,该灯泡亮度的变化情况为( )
A.不变 B.变亮 C.变暗 D.不确定
9.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例
10.已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
A.I= B.I= C.I= D.I=-
二、填空题
11.直角三角形ABCD中,∠BAC=90°,AB=AC=1,以AC为一边在△ABC外部作等腰直角三角形ACD,则线段BD的长为 .
12.在二次函数y=﹣x2+bx+c中,函数y与自变量x的部分对应值如下表:
x ﹣3 ﹣2 ﹣1 1 2 3 4 5 6
y ﹣14 ﹣7 ﹣2 2 m n ﹣7 ﹣14 ﹣23
则m、n的大小关系为 m n.(填“<”,“=”或“>”)
13.如图,在△ABC中,点D是AB上一点,且∠A=∠BCD,S△ADC:S△BDC=5:4,CD=4,则AC长为 .
14.如图,反比例函数y= (x>0)的图象和矩形ABCD都在第一象限内,AD与x轴平行,已知点A的坐标是(2,6),AB=2,AD=4.现将矩形ABCD向下平移m个单位,要使矩形ABCD与反比例函数y= (x>0)的图象有交点,则m的取值范围是 .
15.在温度不变的条件下, 通过一次又一次地对汽缸顶部的活塞加压, 加压后气体对汽缸壁所产生的压强 与汽缸内气体的体积 成反比例, 关于 的函数图象如图 12-2 所示. 若压强由 加压到 , 则气体体积压缩了 .
三、解答题
16.如图,为反比例函数的图像上一点,轴,垂足为.
(1)联结,当时,求反比例函数的解析式;
(2)联结,若,轴上是否存在点,使得,若存在,求出的坐标;若不存在,说明理由.
(3)点在直线上,且,过点作直线轴,交反比例函数的图象于点,若的面积为4,求的值.
17.已知反比例函数的解析式,并且当x=3时,y=4.
(1)求反比例函数的解析式;
(2)当x=-2时,求y的值。
18.甲工程队新建公路,每名工人每天工作8小时,则甲工程队每天可完成600米新建公路.乙工程队比甲工程队少10名工人,每名工人每天工作10小时,则乙工程队每天可完成500米新建公路,假定甲、乙两工程队的每名工人每小时完成的工作量相同,求乙工程队的工人有多少名?
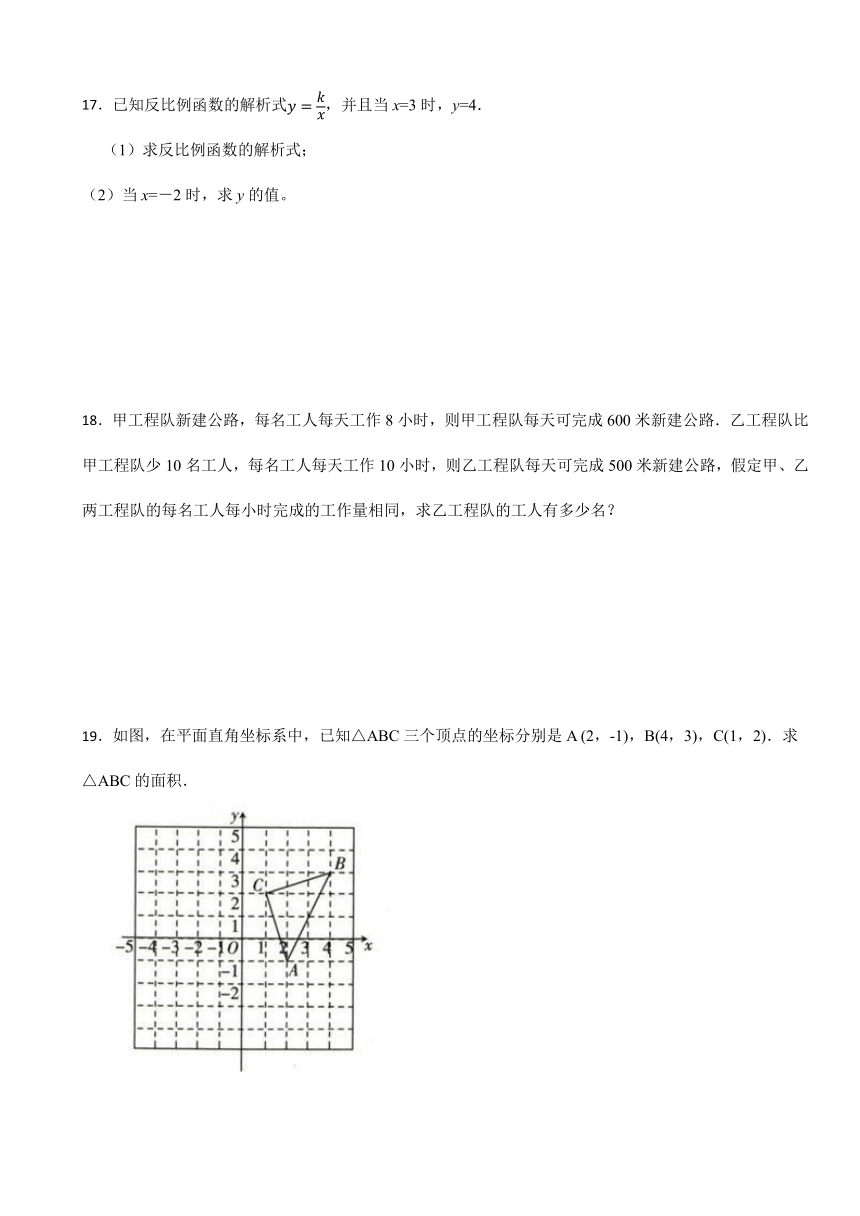
19.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A (2,-1),B(4,3),C(1,2).求△ABC的面积.
20.如图,点在反比例函数的图像上,连接AO并延长、交反比例函数的图像于点B,已知OA=3OB.
(1)求n,k的值.
(2)若点P在x轴上,且△APB的面积为2,求点P的坐标.
21.如图,在中,,,,求的长.
22.如图,直线与反比例函数的图像交于点和点B,四边形是正方形,其中点C,D分别在x轴的负半轴和y轴的正半轴上,过点D作,与反比例函数图象在第二象限内的部分相交于点F.
(1)求m和k的值.
(2)求点D的坐标.
(3)连接,求的面积.
23.在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.
(1)已知A( 2,3),B(5,0),C( , 2).
①当 时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E( , ),其中点E是函数 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
24.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示:
(1)求电流I关于电阻R的函数解析式;
(2)如果以此蓄电池为电源的用电器的限制电流I不能超过10A,请直接写出该用电器可变电阻R应控制在什么范围?
1.B
2.B
3.D
4.A
5.B
6.A
7.B
8.B
9.B
10.C
11.2或 或
12.>
13.6
14.1≤m≤5
15.20
16.(1)
(2)存在,或
(3)或
17.(1)解:
(2)解:-6
18.解:设乙工程队的工人有x名,由题意得
,
解得,经检验是原分式方程的解,且符合题意.
答:乙工程队的工人有20名.
19.解:S△ABC=(3+4)×3×-(1×3)-(2×4)=5
20.(1)n=1,
(2)(-3,0)或(3,0).
21.解:∵,,
∴,
∴.
∵,,
∴
22.(1)
(2)
(3)6
23.(1)35.;t=-3或6.
(2)解:如图1, OD所在的直线交双曲线于点E,矩形OFEG是点O,D,E的一个面积最小的最优覆盖矩形,
∵点D(1,1),
∴OD所在的直线表达式为y=x,
∴点E的坐标为(2,2),
∴OE=, ∴⊙H的半径r =. 如图2,
∵当点E的纵坐标为1时,1=,解得x=4,
∴OE=,
∴⊙H的半径r =, ∴r.
24.(1);
(2)用电器的可变电阻应大于或等于3.6Ω.
班级: 姓名:
亲爱的同学们:
练习开始了,希望你认真审题,细致做题,运用所学知识解决本练习。祝你学习进步!
一、单选题
1.下列函数关系式中属于反比例函数的是( )
A. B. C. D.
2.若反比例函数的图象经过点,则图象必经过点( )
A. B. C. D.
3.如图,点P在反比例函数y= (x>0)的图象上,且横坐标为2.若将点P先向右平移两个单位,再向上平移一个单位后所得的点为点P′.则在第一象限内,经过点P′的反比例函数图象的解析式是( )
A.y=- (x>0) B.y= (x>0)
C.y=- (x>0) D.y= (x>0)
4.已知点,在函数的图象上,当且时,都有,则的取值范围为( )
A. B. C. D.
5.若点(x1,y1)、(x2,y2)和(x3,y3)分别在反比例函数 的图象上,且 ,则下列判断中正确的是( )
A. B. C. D.
6.若点是反比例函数图象上一点,则常数的值为( )
A.3 B. C. D.
7.如图所示,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数和的图象交于点A和点B,若点C是x轴上任意一点,连接,则的面积为( )
A.6 B.7 C.8 D.14
8.根据欧姆定律可知,若一个灯泡的电压保持不变,通过灯泡的电流越大,则灯泡就越亮当电阻时,可测得某灯泡的电流若电压保持不变,电阻减小为时,该灯泡亮度的变化情况为( )
A.不变 B.变亮 C.变暗 D.不确定
9.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例
10.已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
A.I= B.I= C.I= D.I=-
二、填空题
11.直角三角形ABCD中,∠BAC=90°,AB=AC=1,以AC为一边在△ABC外部作等腰直角三角形ACD,则线段BD的长为 .
12.在二次函数y=﹣x2+bx+c中,函数y与自变量x的部分对应值如下表:
x ﹣3 ﹣2 ﹣1 1 2 3 4 5 6
y ﹣14 ﹣7 ﹣2 2 m n ﹣7 ﹣14 ﹣23
则m、n的大小关系为 m n.(填“<”,“=”或“>”)
13.如图,在△ABC中,点D是AB上一点,且∠A=∠BCD,S△ADC:S△BDC=5:4,CD=4,则AC长为 .
14.如图,反比例函数y= (x>0)的图象和矩形ABCD都在第一象限内,AD与x轴平行,已知点A的坐标是(2,6),AB=2,AD=4.现将矩形ABCD向下平移m个单位,要使矩形ABCD与反比例函数y= (x>0)的图象有交点,则m的取值范围是 .
15.在温度不变的条件下, 通过一次又一次地对汽缸顶部的活塞加压, 加压后气体对汽缸壁所产生的压强 与汽缸内气体的体积 成反比例, 关于 的函数图象如图 12-2 所示. 若压强由 加压到 , 则气体体积压缩了 .
三、解答题
16.如图,为反比例函数的图像上一点,轴,垂足为.
(1)联结,当时,求反比例函数的解析式;
(2)联结,若,轴上是否存在点,使得,若存在,求出的坐标;若不存在,说明理由.
(3)点在直线上,且,过点作直线轴,交反比例函数的图象于点,若的面积为4,求的值.
17.已知反比例函数的解析式,并且当x=3时,y=4.
(1)求反比例函数的解析式;
(2)当x=-2时,求y的值。
18.甲工程队新建公路,每名工人每天工作8小时,则甲工程队每天可完成600米新建公路.乙工程队比甲工程队少10名工人,每名工人每天工作10小时,则乙工程队每天可完成500米新建公路,假定甲、乙两工程队的每名工人每小时完成的工作量相同,求乙工程队的工人有多少名?
19.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A (2,-1),B(4,3),C(1,2).求△ABC的面积.
20.如图,点在反比例函数的图像上,连接AO并延长、交反比例函数的图像于点B,已知OA=3OB.
(1)求n,k的值.
(2)若点P在x轴上,且△APB的面积为2,求点P的坐标.
21.如图,在中,,,,求的长.
22.如图,直线与反比例函数的图像交于点和点B,四边形是正方形,其中点C,D分别在x轴的负半轴和y轴的正半轴上,过点D作,与反比例函数图象在第二象限内的部分相交于点F.
(1)求m和k的值.
(2)求点D的坐标.
(3)连接,求的面积.
23.在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.
(1)已知A( 2,3),B(5,0),C( , 2).
①当 时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E( , ),其中点E是函数 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
24.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示:
(1)求电流I关于电阻R的函数解析式;
(2)如果以此蓄电池为电源的用电器的限制电流I不能超过10A,请直接写出该用电器可变电阻R应控制在什么范围?
1.B
2.B
3.D
4.A
5.B
6.A
7.B
8.B
9.B
10.C
11.2或 或
12.>
13.6
14.1≤m≤5
15.20
16.(1)
(2)存在,或
(3)或
17.(1)解:
(2)解:-6
18.解:设乙工程队的工人有x名,由题意得
,
解得,经检验是原分式方程的解,且符合题意.
答:乙工程队的工人有20名.
19.解:S△ABC=(3+4)×3×-(1×3)-(2×4)=5
20.(1)n=1,
(2)(-3,0)或(3,0).
21.解:∵,,
∴,
∴.
∵,,
∴
22.(1)
(2)
(3)6
23.(1)35.;t=-3或6.
(2)解:如图1, OD所在的直线交双曲线于点E,矩形OFEG是点O,D,E的一个面积最小的最优覆盖矩形,
∵点D(1,1),
∴OD所在的直线表达式为y=x,
∴点E的坐标为(2,2),
∴OE=, ∴⊙H的半径r =. 如图2,
∵当点E的纵坐标为1时,1=,解得x=4,
∴OE=,
∴⊙H的半径r =, ∴r.
24.(1);
(2)用电器的可变电阻应大于或等于3.6Ω.
