8.6.1 直线与直线垂直 练习(含解析)-2024-2025学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 8.6.1 直线与直线垂直 练习(含解析)-2024-2025学年高一下学期数学人教A版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 369.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-11 00:00:00 | ||
图片预览

文档简介
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
一、选择题
1.若异面直线a和b所成的角为θ,则θ的取值范围是 ( )
A. B.(0,π)
C. D.(0,π]
2.已知异面直线a,b所成的角为50°,a∥c,则b与c所成的角是 ( )
A.50° B.40°
C.50°或130° D.130°
3.直三棱柱ABC-A1B1C1中,AB⊥AC,则在该直三棱柱的所有棱中,与AC垂直且异面的有 ( )
A.1条 B.2条
C.3条 D.4条
4.在空间四边形ABCD中,AC⊥BD,则顺次连接四边的中点形成的四边形一定是 ( )
A.空间四边形 B.矩形
C.菱形 D.正方形
5.如图,正方体ABCD-A1B1C1D1的12条棱所在的直线中与直线BC1所成的角为的条数为 ( )
A.6 B.8
C.10 D.12
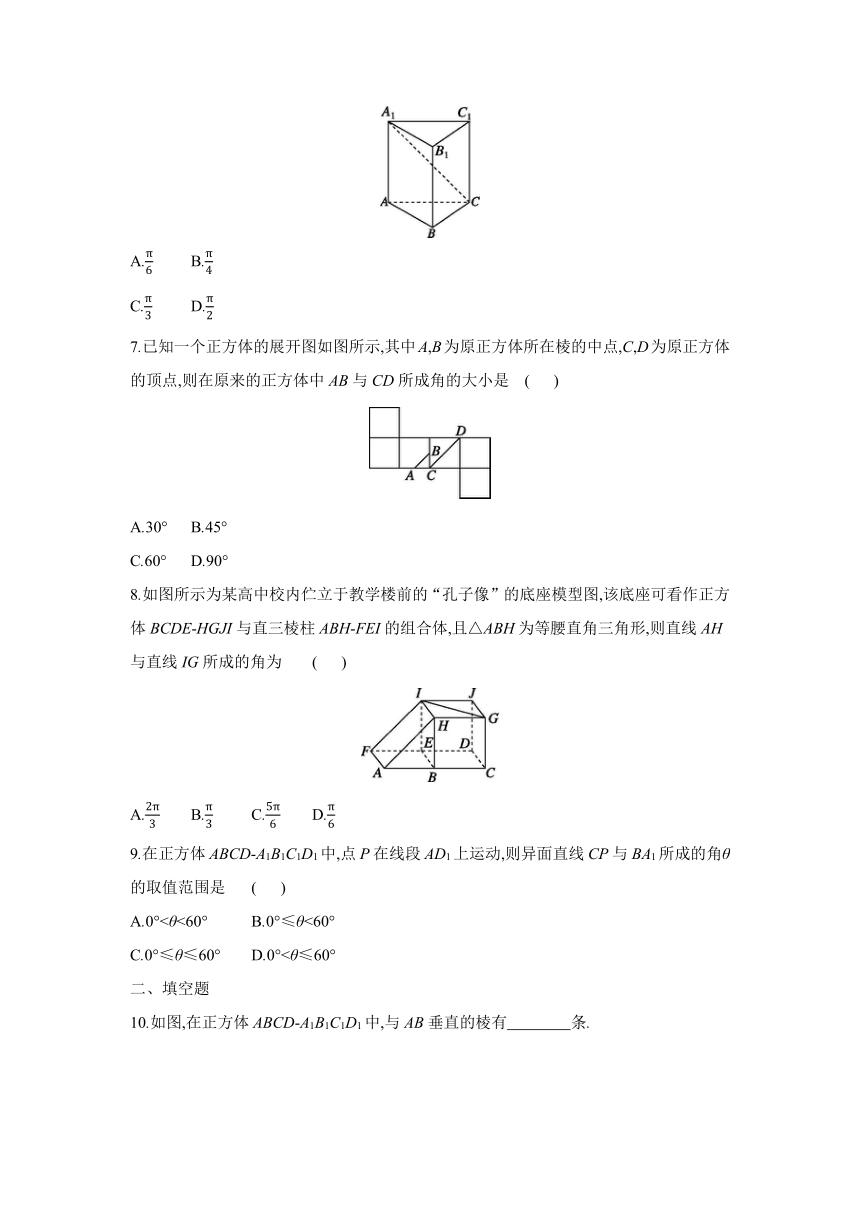
6.如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,若AA1=AC=BC=1,则异面直线A1C与AB所成角的大小是 ( )
A. B.
C. D.
7.已知一个正方体的展开图如图所示,其中A,B为原正方体所在棱的中点,C,D为原正方体的顶点,则在原来的正方体中AB与CD所成角的大小是 ( )
A.30° B.45°
C.60° D.90°
8.如图所示为某高中校内伫立于教学楼前的“孔子像”的底座模型图,该底座可看作正方体BCDE-HGJI与直三棱柱ABH-FEI的组合体,且△ABH为等腰直角三角形,则直线AH与直线IG所成的角为 ( )
A. B. C. D.
9.在正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,则异面直线CP与BA1所成的角θ的取值范围是 ( )
A.0°<θ<60° B.0°≤θ<60°
C.0°≤θ≤60° D.0°<θ≤60°
二、填空题
10.如图,在正方体ABCD-A1B1C1D1中,与AB垂直的棱有 条.
11.在空间四边形ABCD中,AB=CD,E,F分别为BC,AD的中点,若异面直线AB与CD所成的角为30°,则异面直线EF与AB所成的角的大小为 .
12.如图,ABC-A1B1C1是一个正三棱台,而且下底面边长为4,上底面边长和侧棱长都为2,则异面直线A1C与BB1所成角的余弦值为 .
三、解答题
13.如图,在三棱锥P-ABC中,PA=4,BC=6.
(1)在该棱锥的6条棱所在的直线中,共有多少对异面直线 请一一列出.
(2)若棱PB的中点为M,棱AC的中点为N,MN=4,求异面直线PA与BC所成的角的余弦值.
14.已知圆柱的底面半径为,四边形ABCD为其轴截面,若点E为上底面圆弧的中点,异面直线DE与BC所成的角为,求圆柱的表面积.
15.如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为底面ABCD内(包括边界)的动点,满足D1P与直线CC1所成角的大小为,则线段DP扫过的面积为 .
16.空间中A,B,C,D四点任意两点间的距离都等于a,E为BC的中点,在由A,B,C,D确定的四个等边三角形中,求与AE异面的三角形中线与AE所成角的余弦值.
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
1.C [解析] 根据异面直线的概念可得,θ的取值范围是,故选C.
2.A [解析] 在直线b上取一点作c'∥c,如图.因为c∥a,所以c'∥a,则相交直线b,c'所成的角就是异面直线a,b所成的角,所以相交直线b,c'所成的角为50°,所以b与c所成的角是50°.
3.B [解析] 如图,直三棱柱ABC-A1B1C1中,AB⊥AC,则在该直三棱柱的所有棱中,与AC垂直且异面的有A1B1和BB1,共2条.故选B.
4.B [解析] 如图,易知四边形EFGH为平行四边形.∵E,F分别为AB,BC的中点,∴EF∥AC.同理可得FG∥BD,∴∠EFG或其补角为AC与BD所成的角.∵AC与BD所成的角为90°,∴∠EFG=90°,故四边形EFGH为矩形.
5.B [解析] 因为∠CBC1=,所以BC与直线BC1所成的角为,又BC∥AD∥A1D1∥B1C1,所以AD,A1D1,B1C1与直线BC1所成的角为.同理可得BB1,CC1,DD1,AA1与直线BC1所成的角为.又AB,CD,C1D1,A1B1与直线BC1所成的角为,所以与直线BC1所成的角为的棱有8条.故选B.
6.C [解析] 如图所示,连接B1C.∵A1B1∥AB ,∴∠B1A1C或其补角即为异面直线A1C与AB所成的角.∵在直三棱柱ABC-A1B1C1中,AC⊥BC,AA1=AC=BC=1,∴A1C=,B1C=,AB=A1B1=.在△B1A1C中,∵A1B1=A1C=B1C=,∴△B1A1C是正三角形,∴∠B1A1C=.故选C.
7.C [解析] 将展开图还原为正方体,如图,其中EG,EF,FG分别为所在面的对角线.因为A,B分别为相应棱的中点,所以EF∥AB,易知CD∥EG,所以∠FEG或其补角为AB与CD所成的角,又因为EG=EF=FG,所以∠FEG=60°,即AB与CD所成角的大小是60°.故选C.
8.B [解析] 如图,连接FC,FG,易知AH∥FI,所以∠FIG或其补角为直线AH与直线IG所成的角.设BC=1,则IG=,FC=,FI=,CG=1.在Rt△FCG中,FG===.在△FIG中,由余弦定理得cos∠FIG===-,又∠FIG∈(0,π),所以∠FIG=,又直线AH与直线IG所成角的取值范围为,所以直线AH与直线IG所成的角为.
9.D [解析] 如图,连接CD1,AC.易知CD1∥BA1,所以∠D1CP或其补角即为CP与BA1所成的角,又易知∠D1CP始终是锐角,所以θ=∠D1CP.当点P从点D1向点A运动时,∠D1CP从0°增大到60°,但当点P与D1重合时,CP∥BA1,此时CP与BA1不是异面直线,不符合题意,所以异面直线CP与BA1所成的角θ的取值范围是0°<θ≤60°.故选D.
10.8 [解析] 与AB垂直的棱有AA1,BB1,CC1,DD1,AD,BC,A1D1,B1C1,共8条.
11.75°或15° [解析] 连接AC,取AC的中点G,连接GE与GF,∵异面直线AB与CD所成的角为30°,且EG∥AB,FG∥CD,∴∠EGF=30°或∠EGF=150°.∵EG∥AB,∴∠GEF为异面直线AB与EF所成的角.由AB=CD,得GE=GF,∴∠GEF=75°或∠GEF=15°,∴EF与AB所成的角是75°或15°.
12. [解析] 如图,取AB的中点D,连接A1D,CD.因为A1B1∥DB且A1B1=DB,所以四边形A1B1BD为平行四边形,所以A1D∥BB1,则∠CA1D(或其补角)即为异面直线A1C与BB1所成的角.因为AA1=A1B1=AB=BB1=2,所以平行四边形A1B1BD为菱形,又AD=DB=2,所以△ADA1为等边三角形,所以∠A1AB=60°,所以∠A1AC=60°,在△A1AC中,由余弦定理得A1C===2.又CD==2, A1D=2,所以在△CA1D中,由余弦定理得cos∠CA1D==,则异面直线A1C与BB1所成角的余弦值为.
13.解:(1)在该棱锥的6条棱所在的直线中,共有3对异面直线,分别是PA与BC,PB与AC,PC与AB.
(2)如图,取AB的中点O,连接OM,ON,因为PB的中点为M,AC的中点为N,所以OM∥PA,ON∥BC,所以异面直线PA与BC所成的角为∠MON或其补角.
因为PA=4,BC=6,所以OM=2,ON=3,又MN=4,所以在△MON中,由余弦定理可得cos∠MON===-,所以异面直线PA与BC所成的角的余弦值为.
14.解:如图,设底面圆心为O,则O为CD的中点,过点E作EF∥BC,交圆O于F,
连接OE,OF,DF,∵BC∥EF,∠DEF为锐角,
∴∠DEF为异面直线DE与BC所成的角,∴∠DEF=.
∵点E为上底面圆弧的中点,∴点F为下底面圆弧的中点,∴CD⊥OF,∴DF==2,
又EF⊥DF,∠DEF=,∴EF=2,
则圆柱的表面积S=2π×EF+2π×()2=4(+1)π.
15. [解析] 由题意知DD1∥CC1,要使D1P与直线CC1所成角的大小为,只需D1P与直线DD1所成角的大小为,∴∠DD1P=,又DD1=1,DD1⊥DP,∴DP=.如图所示,P的轨迹是以D为圆心,为半径的四分之一圆,∴线段DP扫过的面积为××π=.
16.解:如图①所示,AE与中线BF为异面直线.
连接DE,取DE的中点G,连接FG,BG,则GF∥AE,所以∠BFG或其补角是异面直线AE与BF所成的角.
又GF=a,BF=a,BG==a,
则cos∠BFG==,
所以异面直线AE与BF所成角的余弦值为.
如图②所示,AE与中线DH为异面直线.
取BE的中点I,连接HI,DI,DE,则HI∥AE,所以∠IHD或其补角是异面直线AE与DH所成的角.
又DH=a,HI=a,
DI===a,
则cos∠IHD==,
所以异面直线AE与DH所成角的余弦值为.
如图③所示,AE与中线CJ为异面直线.
取BJ的中点K,连接EK,AK,AJ,则EK∥CJ,所以∠AEK或其补角是异面直线AE和CJ所成的角.
又AE=a,EK=a,AK==a,
则cos∠AEK==,
所以异面直线AE与CJ所成角的余弦值为.
同理,易知其他与AE异面的中线与AE所成角的余弦值也为或.
综上,与AE异面的三角形中线与AE所成角的余弦值为或.
8.6.1 直线与直线垂直
一、选择题
1.若异面直线a和b所成的角为θ,则θ的取值范围是 ( )
A. B.(0,π)
C. D.(0,π]
2.已知异面直线a,b所成的角为50°,a∥c,则b与c所成的角是 ( )
A.50° B.40°
C.50°或130° D.130°
3.直三棱柱ABC-A1B1C1中,AB⊥AC,则在该直三棱柱的所有棱中,与AC垂直且异面的有 ( )
A.1条 B.2条
C.3条 D.4条
4.在空间四边形ABCD中,AC⊥BD,则顺次连接四边的中点形成的四边形一定是 ( )
A.空间四边形 B.矩形
C.菱形 D.正方形
5.如图,正方体ABCD-A1B1C1D1的12条棱所在的直线中与直线BC1所成的角为的条数为 ( )
A.6 B.8
C.10 D.12
6.如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,若AA1=AC=BC=1,则异面直线A1C与AB所成角的大小是 ( )
A. B.
C. D.
7.已知一个正方体的展开图如图所示,其中A,B为原正方体所在棱的中点,C,D为原正方体的顶点,则在原来的正方体中AB与CD所成角的大小是 ( )
A.30° B.45°
C.60° D.90°
8.如图所示为某高中校内伫立于教学楼前的“孔子像”的底座模型图,该底座可看作正方体BCDE-HGJI与直三棱柱ABH-FEI的组合体,且△ABH为等腰直角三角形,则直线AH与直线IG所成的角为 ( )
A. B. C. D.
9.在正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,则异面直线CP与BA1所成的角θ的取值范围是 ( )
A.0°<θ<60° B.0°≤θ<60°
C.0°≤θ≤60° D.0°<θ≤60°
二、填空题
10.如图,在正方体ABCD-A1B1C1D1中,与AB垂直的棱有 条.
11.在空间四边形ABCD中,AB=CD,E,F分别为BC,AD的中点,若异面直线AB与CD所成的角为30°,则异面直线EF与AB所成的角的大小为 .
12.如图,ABC-A1B1C1是一个正三棱台,而且下底面边长为4,上底面边长和侧棱长都为2,则异面直线A1C与BB1所成角的余弦值为 .
三、解答题
13.如图,在三棱锥P-ABC中,PA=4,BC=6.
(1)在该棱锥的6条棱所在的直线中,共有多少对异面直线 请一一列出.
(2)若棱PB的中点为M,棱AC的中点为N,MN=4,求异面直线PA与BC所成的角的余弦值.
14.已知圆柱的底面半径为,四边形ABCD为其轴截面,若点E为上底面圆弧的中点,异面直线DE与BC所成的角为,求圆柱的表面积.
15.如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为底面ABCD内(包括边界)的动点,满足D1P与直线CC1所成角的大小为,则线段DP扫过的面积为 .
16.空间中A,B,C,D四点任意两点间的距离都等于a,E为BC的中点,在由A,B,C,D确定的四个等边三角形中,求与AE异面的三角形中线与AE所成角的余弦值.
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
1.C [解析] 根据异面直线的概念可得,θ的取值范围是,故选C.
2.A [解析] 在直线b上取一点作c'∥c,如图.因为c∥a,所以c'∥a,则相交直线b,c'所成的角就是异面直线a,b所成的角,所以相交直线b,c'所成的角为50°,所以b与c所成的角是50°.
3.B [解析] 如图,直三棱柱ABC-A1B1C1中,AB⊥AC,则在该直三棱柱的所有棱中,与AC垂直且异面的有A1B1和BB1,共2条.故选B.
4.B [解析] 如图,易知四边形EFGH为平行四边形.∵E,F分别为AB,BC的中点,∴EF∥AC.同理可得FG∥BD,∴∠EFG或其补角为AC与BD所成的角.∵AC与BD所成的角为90°,∴∠EFG=90°,故四边形EFGH为矩形.
5.B [解析] 因为∠CBC1=,所以BC与直线BC1所成的角为,又BC∥AD∥A1D1∥B1C1,所以AD,A1D1,B1C1与直线BC1所成的角为.同理可得BB1,CC1,DD1,AA1与直线BC1所成的角为.又AB,CD,C1D1,A1B1与直线BC1所成的角为,所以与直线BC1所成的角为的棱有8条.故选B.
6.C [解析] 如图所示,连接B1C.∵A1B1∥AB ,∴∠B1A1C或其补角即为异面直线A1C与AB所成的角.∵在直三棱柱ABC-A1B1C1中,AC⊥BC,AA1=AC=BC=1,∴A1C=,B1C=,AB=A1B1=.在△B1A1C中,∵A1B1=A1C=B1C=,∴△B1A1C是正三角形,∴∠B1A1C=.故选C.
7.C [解析] 将展开图还原为正方体,如图,其中EG,EF,FG分别为所在面的对角线.因为A,B分别为相应棱的中点,所以EF∥AB,易知CD∥EG,所以∠FEG或其补角为AB与CD所成的角,又因为EG=EF=FG,所以∠FEG=60°,即AB与CD所成角的大小是60°.故选C.
8.B [解析] 如图,连接FC,FG,易知AH∥FI,所以∠FIG或其补角为直线AH与直线IG所成的角.设BC=1,则IG=,FC=,FI=,CG=1.在Rt△FCG中,FG===.在△FIG中,由余弦定理得cos∠FIG===-,又∠FIG∈(0,π),所以∠FIG=,又直线AH与直线IG所成角的取值范围为,所以直线AH与直线IG所成的角为.
9.D [解析] 如图,连接CD1,AC.易知CD1∥BA1,所以∠D1CP或其补角即为CP与BA1所成的角,又易知∠D1CP始终是锐角,所以θ=∠D1CP.当点P从点D1向点A运动时,∠D1CP从0°增大到60°,但当点P与D1重合时,CP∥BA1,此时CP与BA1不是异面直线,不符合题意,所以异面直线CP与BA1所成的角θ的取值范围是0°<θ≤60°.故选D.
10.8 [解析] 与AB垂直的棱有AA1,BB1,CC1,DD1,AD,BC,A1D1,B1C1,共8条.
11.75°或15° [解析] 连接AC,取AC的中点G,连接GE与GF,∵异面直线AB与CD所成的角为30°,且EG∥AB,FG∥CD,∴∠EGF=30°或∠EGF=150°.∵EG∥AB,∴∠GEF为异面直线AB与EF所成的角.由AB=CD,得GE=GF,∴∠GEF=75°或∠GEF=15°,∴EF与AB所成的角是75°或15°.
12. [解析] 如图,取AB的中点D,连接A1D,CD.因为A1B1∥DB且A1B1=DB,所以四边形A1B1BD为平行四边形,所以A1D∥BB1,则∠CA1D(或其补角)即为异面直线A1C与BB1所成的角.因为AA1=A1B1=AB=BB1=2,所以平行四边形A1B1BD为菱形,又AD=DB=2,所以△ADA1为等边三角形,所以∠A1AB=60°,所以∠A1AC=60°,在△A1AC中,由余弦定理得A1C===2.又CD==2, A1D=2,所以在△CA1D中,由余弦定理得cos∠CA1D==,则异面直线A1C与BB1所成角的余弦值为.
13.解:(1)在该棱锥的6条棱所在的直线中,共有3对异面直线,分别是PA与BC,PB与AC,PC与AB.
(2)如图,取AB的中点O,连接OM,ON,因为PB的中点为M,AC的中点为N,所以OM∥PA,ON∥BC,所以异面直线PA与BC所成的角为∠MON或其补角.
因为PA=4,BC=6,所以OM=2,ON=3,又MN=4,所以在△MON中,由余弦定理可得cos∠MON===-,所以异面直线PA与BC所成的角的余弦值为.
14.解:如图,设底面圆心为O,则O为CD的中点,过点E作EF∥BC,交圆O于F,
连接OE,OF,DF,∵BC∥EF,∠DEF为锐角,
∴∠DEF为异面直线DE与BC所成的角,∴∠DEF=.
∵点E为上底面圆弧的中点,∴点F为下底面圆弧的中点,∴CD⊥OF,∴DF==2,
又EF⊥DF,∠DEF=,∴EF=2,
则圆柱的表面积S=2π×EF+2π×()2=4(+1)π.
15. [解析] 由题意知DD1∥CC1,要使D1P与直线CC1所成角的大小为,只需D1P与直线DD1所成角的大小为,∴∠DD1P=,又DD1=1,DD1⊥DP,∴DP=.如图所示,P的轨迹是以D为圆心,为半径的四分之一圆,∴线段DP扫过的面积为××π=.
16.解:如图①所示,AE与中线BF为异面直线.
连接DE,取DE的中点G,连接FG,BG,则GF∥AE,所以∠BFG或其补角是异面直线AE与BF所成的角.
又GF=a,BF=a,BG==a,
则cos∠BFG==,
所以异面直线AE与BF所成角的余弦值为.
如图②所示,AE与中线DH为异面直线.
取BE的中点I,连接HI,DI,DE,则HI∥AE,所以∠IHD或其补角是异面直线AE与DH所成的角.
又DH=a,HI=a,
DI===a,
则cos∠IHD==,
所以异面直线AE与DH所成角的余弦值为.
如图③所示,AE与中线CJ为异面直线.
取BJ的中点K,连接EK,AK,AJ,则EK∥CJ,所以∠AEK或其补角是异面直线AE和CJ所成的角.
又AE=a,EK=a,AK==a,
则cos∠AEK==,
所以异面直线AE与CJ所成角的余弦值为.
同理,易知其他与AE异面的中线与AE所成角的余弦值也为或.
综上,与AE异面的三角形中线与AE所成角的余弦值为或.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
