9.2.3 总体集中趋势的估计 练习(含解析)-2024-2025学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 9.2.3 总体集中趋势的估计 练习(含解析)-2024-2025学年高一下学期数学人教A版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 152.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-11 00:00:00 | ||
图片预览



文档简介
9.2.3 总体集中趋势的估计
一、选择题
1.下列数字特征一定会在原始数据中出现的是 ( )
A.众数 B.中位数
C.平均数 D.都不会
2.在某知识竞赛中,共设有10道题,每道题答对计1分,答错不计分,经统计,10位选手的得分情况如下表:
得分(X) 6 7 8 9 10
人数 1 2 4 2 1
则这10位选手得分的中位数和众数分别为 ( )
A.9,8 B.8,8
C.9,8.5 D.8.5,9
3.[2024·重庆西南大学附中高一月考] 样本中共有5个个体,其值分别为x1,x2,x3,x4,x5.若该样本的平均数为3,则3x1+1,3x2+1,3x3+1,3x4+1,3x5+1的平均数为 ( )
A.1 B.3 C.9 D.10
4.[2024·河南南阳六校高一期末] 已知100个数据的中位数是8,则下列说法正确的是 ( )
A.这100个数据中一定有且仅有50个数小于或等于8
B.把这100个数据从小到大排列后,8是第50个数据
C.把这100个数据从小到大排列后,8是第50和第51个数据的平均数
D.把这100个数据从小到大排列后,8是第50和第49个数据的平均数
5.众数、平均数、中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关.在如图所示的分布形态中,平均数、众数和中位数的大小关系是 ( )
A.众数<中位数<平均数
B.平均数<众数<中位数
C.中位数<平均数<众数
D.众数<平均数<中位数
6.某校组织学生参加航天知识竞赛,现从中随机抽取100名学生统计其成绩,得到的频率分布直方图如图所示,设样本数据的75%分位数为x,众数为y,则 ( )
A.x=88,y=90 B.x=83,y=90
C.x=83,y=85 D.x=88,y=85
7.[2024·江西上饶沙溪中学高一期末] 某市政府为了制定居民节约用水相关政策,抽样调查了该市200户居民月均用水量(单位:t),根据所得数据绘制成的频率分布直方图如图,则下列说法不正确的是 ( )
A.图中小矩形ABCD的面积为0.24
B.估计该市居民月均用水量的众数为6 t
C.估计该市有85%的居民月均用水量不超过19 t
D.估计这200户居民月均用水量的中位数大于平均数
8.(多选题)[2024·山东日照一中高一月考] 某科技攻关青年团队共有10人,其年龄(单位:岁)分布如下表所示,则这10个人年龄的 ( )
年龄 45 40 36 32 29 28
人数 1 2 1 3 2 1
A.中位数是34
B.众数是32
C.第25百分位数是29
D.平均数为34.3
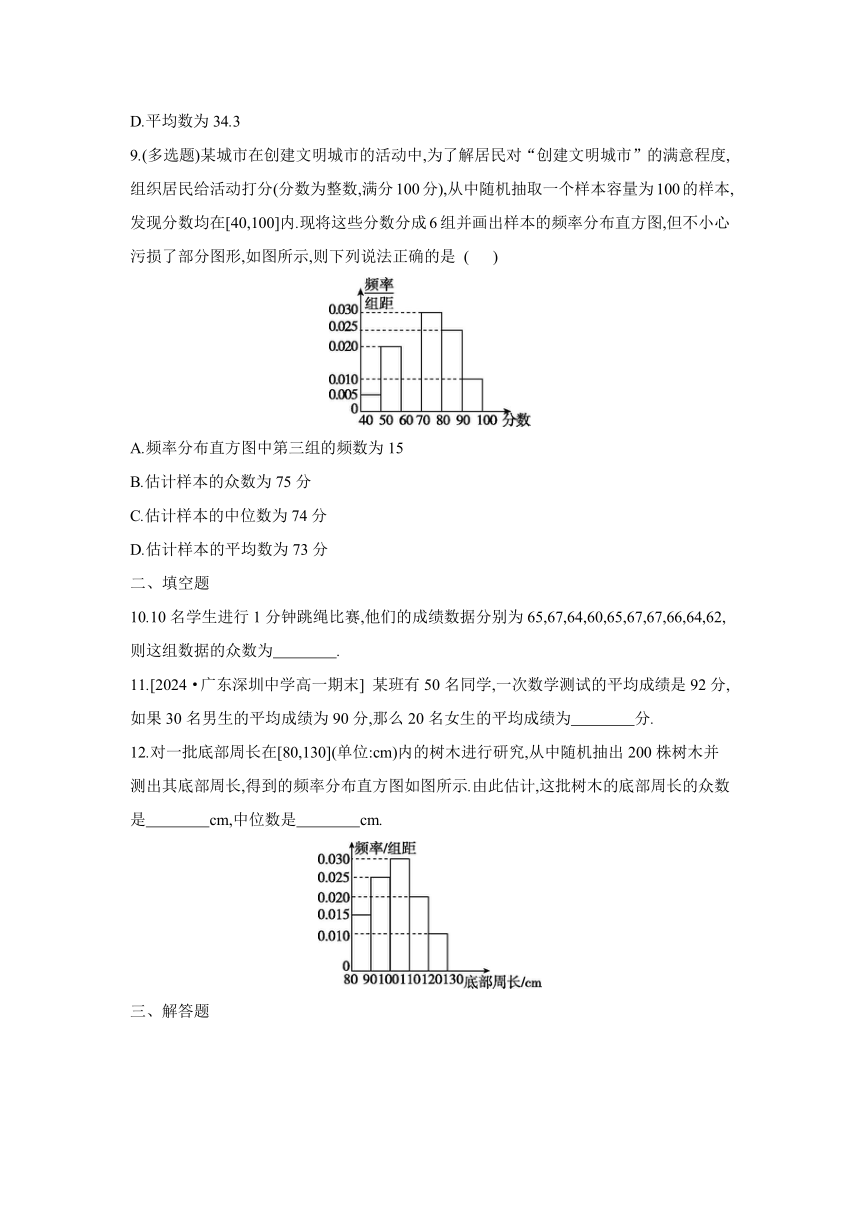
9.(多选题)某城市在创建文明城市的活动中,为了解居民对“创建文明城市”的满意程度,组织居民给活动打分(分数为整数,满分100分),从中随机抽取一个样本容量为100的样本,发现分数均在[40,100]内.现将这些分数分成6组并画出样本的频率分布直方图,但不小心污损了部分图形,如图所示,则下列说法正确的是 ( )
A.频率分布直方图中第三组的频数为15
B.估计样本的众数为75分
C.估计样本的中位数为74分
D.估计样本的平均数为73分
二、填空题
10.10名学生进行1分钟跳绳比赛,他们的成绩数据分别为65,67,64,60,65,67,67,66,64,62,则这组数据的众数为 .
11.[2024·广东深圳中学高一期末] 某班有50名同学,一次数学测试的平均成绩是92分,如果30名男生的平均成绩为90分,那么20名女生的平均成绩为 分.
12.对一批底部周长在[80,130](单位:cm)内的树木进行研究,从中随机抽出200株树木并测出其底部周长,得到的频率分布直方图如图所示.由此估计,这批树木的底部周长的众数是 cm,中位数是 cm.
三、解答题
13.从某校高一年级新生中随机抽取一个容量为20的身高样本,数据如下(单位:cm,数据间无大小顺序要求):152,155,158,164,164,165,165,165,166,167,168,168,169,170,170,170,171,x,174,175.
(1)若x为这组数据的一个众数,求x的取值集合;
(2)若将样本数据按从小到大的顺序排列,第90百分位数是173,求x的值;
(3)若x=174,试估计该校高一年级新生的平均身高.
14.果切是一种新型水果售卖方式,商家通过对整果进行消洗、去皮、去核、冷藏等操作后,包装组合销售.
(1)统计得到10名果切消费者每周购买果切的次数依次为1,7,4,7,4,6,6,3,7,5,求这10个数据的平均数与方差s2.
(2)统计600名果切消费者的年龄,他们的年龄均在5岁到55岁之间,将所得数据按照[5,15),[15,25),[25,35),[35,45),[45,55]分组,得到的频率分布直方图如图.
①求这600名果切消费者中年龄不低于35岁的人数;
②估计这600名果切消费者年龄的中位数a及平均数(结果保留整数).
15.某工厂生产销售了30双皮鞋,其中各种尺寸的销售量如下表所示:
鞋的尺寸(cm) 22 22.5 23 23.5 24 24.5 25
销售量(双) 1 2 4 14 5 3 1
(1)这30双鞋尺寸的平均数为 ,中位数为 ,众数为 ;
(2)从实际出发,问题(1)中的众数对指导生产的意义是 .
16.[2024·重庆十八中高一月考] 2023年以来,某区把垃圾分类纳入积分,建立文明账户,市民以行动换积分,以积分转习惯.区政府为了了解4月份甲、乙两个社区居民换积分的情况,分别从甲、乙两个社区各抽取10人,记录下他们的积分(单位:分),并进行整理和分析(积分用x表示,共分为4组:A:x<70;B:70≤x<80,C:80≤x<90,D:90≤x≤100),下面给出了部分信息:
甲社区10人的积分:47,56,68,71,83,83,85,90,91,94;
乙社区10人的积分在C组中的积分为81,83,84,84.
乙社区10人的积分等级扇形图如图.
两组数据的平均数、中位数、众数如下表所示:
社区 平均数 中位数 众数
甲 76.8 83 b
乙 76.8 a 84
根据以上信息,解答下列问题.
(1)求a,b,m的值.
(2)根据以上数据,你认为哪个社区在此次垃圾分类换积分活动中表现更好 请说明理由(一条即可).
(3)若4月份甲社区有700人参与活动,乙社区有800人参与活动,用样本估计总体,估计4月份甲、乙两个社区积分在80分及以上的人数.
9.2.3 总体集中趋势的估计
1.A [解析] 众数是在一组数据中出现次数最多的数,所以一定会在原始数据中出现.
2.B [解析] 将这10位选手的得分从小到大排列为6,7,7,8,8,8,8,9,9,10,可知中位数为8,且8出现的次数最多,故众数为8.故选B.
3.D [解析] 由题意得=3,故x1+x2+x3+x4+x5=15,则===10.故选D.
4.C [解析] 若这100个数都是8,则这100个数据的中位数是8,故A错误;因为100为偶数,所以把这100个数据从小到大排列后,第50和第51个数据的平均数为中位数,故C正确,B,D错误.故选C.
5.A [解析] 众数是最高矩形的中点横坐标,因此众数在第二组的中点处.因为直方图在右边拖尾,所以平均数大于中位数,又中位数左边和右边的矩形面积之和相等,所以中位数在第二组右边,因此有众数<中位数<平均数.故选A.
6.D [解析] 由题意得(0.005+0.03+a+0.015)×10=1,解得a=0.05,因为0.05+0.3=0.35,0.05+0.3+0.5=0.85,0.35<0.75<0.85,所以样本数据的75%分位数x位于[80,90)内,则0.35+(x-80)×0.05=0.75,解得x=88.因为样本数据中位于[80,90)内的频率最大,所以众数y==85,故选D.
7.D [解析] 由4×(0.01+0.075+a+0.045+0.03+0.02+0.01)=1,可得a=0.06,所以S矩形ABCD=4×0.06=0.24,故A中说法正确;估计该市居民月均用水量的众数为=6(t),故B中说法正确;估计该市居民月均用水量不超过19 t的频率为4×(0.01+0.075+0.06+0.045)+×4×0.03=0.76+0.09=0.85,故C中说法正确;设这200户居民月均用水量的中位数为x1,因为第一个矩形的面积为0.04,第二个矩形的面积为0.3,第三个矩形的面积为0.24,所以中位数x1∈[8,12],由x1=8+×4=8+=,可估计这200户居民月均用水量的中位数为t,估计这200户居民月均用水量的平均数=4×0.01×2+4×0.075×6+4×0.06×10+4×0.045×14+4×0.03×18+4×0.02×22+4×0.01×26=11.76(t),因为<11<11.76,所以估计这200户居民月均用水量的中位数小于平均数,故D中说法不正确.故选D.
8.BCD [解析] 把这10个人的年龄从小到大排列为28,29,29,32,32,32,36,40,40,45,易知这组数据的中位数为32,众数为32,故A错误,B正确;由25%×10=2.5,得这组数据的第25百分位数是第3个数,为29,故C正确;这组数据的平均数==34.3,故D正确.故选BCD.
9.BD [解析] 对于A,因为分数在[60,70]内的频率为1-10×(0.005+0.020+0.030+0.025+0.010)=0.10,所以第三组的频数为100×0.10=10,故A错误;对于B,由图可估计样本的众数为75分,故B正确;对于C,因为10×(0.005+0.020+0.010)=0.35<0.5,10×(0.005+0.020+0.010+0.030)=0.65>0.5,所以中位数位于[70,80]内,设中位数为x,则0.35+0.03(x-70)=0.5,解得x=75,所以估计样本的中位数为75分,故C错误;对于D,估计样本的平均数为(45×0.005+55×0.020+65×0.010+75×0.030+85×0.025+95×0.010)×10=73(分),故D正确,故选BD.
10.67 [解析] 数据65,67,64,60,65,67,67,66,64,62中,出现次数最多的数据是67,即众数为67.
11.95 [解析] 设20名女生的平均成绩为,由题意得50×92=30×90+20×,解得=95(分).
12.105 [解析] 由题图,估计这批树木的底部周长的众数是=105(cm),中位数是+100=+100=(cm).
13.解:(1)若x为这组数据的一个众数,则x的可能取值为164,165,168,170,
即x的取值集合为{164,165,168,170}.
(2)因为样本数据的第90百分位数是173,且20×90%=18,
所以样本数据的第90百分位数为=173,
所以x=172.
(3)若x=174,则估计该校高一年级新生的平均身高为
×(152+155+158+164+164+165+165+165+166+167+168+168+169+170+170+170+171+174+174+175)=166.5(cm).
14.解:(1)==5,
s2=×[(1-5)2+(3-5)2+2×(4-5)2+(5-5)2+2×(6-5)2+3×(7-5)2]=3.6.
(2)①这600名果切消费者中年龄不低于35岁的人数为(0.015+0.005)×10×600=120.
②由0.020×10=0.2<0.5,(0.020+0.035)×10=0.55>0.5,可得15所以估计这600名果切消费者年龄的中位数约为24岁.
估计这600名果切消费者年龄的平均数=10×0.020×10+20×0.035×10+30×0.025×10+40×0.015×10+50×0.005×10=25(岁).
15.(1)23.55 cm 23.5 cm 23.5 cm (2)尺寸为23.5 cm的鞋销量最好,厂家应多生产 [解析] (1)30双鞋尺寸的平均数=×(22×1+22.5×2+23×4+23.5×14+24×5+24.5×3+25×1)=23.55(cm).由于尺寸小于23.5 cm的销售量为1+2+4=7(双),尺寸大于23.5 cm的销售量为5+3+1=9(双),故将30个数据按从小到大的顺序排列,处于正中间位置的两个数据均为23.5,从而中位数为23.5 cm.因为数据23.5共出现14次,出现次数最多,所以众数也为23.5 cm.
(2)尺寸为23.5 cm的鞋销量最好,厂家应多生产.
16.解:(1)因为甲社区10人的积分中出现次数最多的数据为83,所以b=83.
由乙社区10人的积分等级扇形图可得,乙社区10人的积分在A组的人数为10×10%=1,在B组的人数为10×20%=2,因为乙社区10人的积分在C组中的积分为81,83,84,84,所以乙社区10人的积分从小到大排列后的第5和第6个数据分别为83,84,
所以a=×(83+84)=83.5.
因为乙社区10人的积分在D组的人数为10-1-2-4=3,所以D组人数所占的百分比为×100%=30%,所以m=30.
(2)乙社区在此次垃圾分类换积分活动中表现更好,理由如下:
因为虽然甲、乙两个社区积分的平均数相同,但是乙社区的中位数和众数均比甲社区高,所以乙社区在此次垃圾分类换积分活动中表现更好.
(3)在样本中,甲社区积分在80分及以上的人数所占的比例为=0.6,乙社区积分在80分及以上的人数所占的比例为=0.7,所以估计4月份甲、乙两个社区积分在80分及以上的人数为0.6×700+0.7×800=980.
一、选择题
1.下列数字特征一定会在原始数据中出现的是 ( )
A.众数 B.中位数
C.平均数 D.都不会
2.在某知识竞赛中,共设有10道题,每道题答对计1分,答错不计分,经统计,10位选手的得分情况如下表:
得分(X) 6 7 8 9 10
人数 1 2 4 2 1
则这10位选手得分的中位数和众数分别为 ( )
A.9,8 B.8,8
C.9,8.5 D.8.5,9
3.[2024·重庆西南大学附中高一月考] 样本中共有5个个体,其值分别为x1,x2,x3,x4,x5.若该样本的平均数为3,则3x1+1,3x2+1,3x3+1,3x4+1,3x5+1的平均数为 ( )
A.1 B.3 C.9 D.10
4.[2024·河南南阳六校高一期末] 已知100个数据的中位数是8,则下列说法正确的是 ( )
A.这100个数据中一定有且仅有50个数小于或等于8
B.把这100个数据从小到大排列后,8是第50个数据
C.把这100个数据从小到大排列后,8是第50和第51个数据的平均数
D.把这100个数据从小到大排列后,8是第50和第49个数据的平均数
5.众数、平均数、中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关.在如图所示的分布形态中,平均数、众数和中位数的大小关系是 ( )
A.众数<中位数<平均数
B.平均数<众数<中位数
C.中位数<平均数<众数
D.众数<平均数<中位数
6.某校组织学生参加航天知识竞赛,现从中随机抽取100名学生统计其成绩,得到的频率分布直方图如图所示,设样本数据的75%分位数为x,众数为y,则 ( )
A.x=88,y=90 B.x=83,y=90
C.x=83,y=85 D.x=88,y=85
7.[2024·江西上饶沙溪中学高一期末] 某市政府为了制定居民节约用水相关政策,抽样调查了该市200户居民月均用水量(单位:t),根据所得数据绘制成的频率分布直方图如图,则下列说法不正确的是 ( )
A.图中小矩形ABCD的面积为0.24
B.估计该市居民月均用水量的众数为6 t
C.估计该市有85%的居民月均用水量不超过19 t
D.估计这200户居民月均用水量的中位数大于平均数
8.(多选题)[2024·山东日照一中高一月考] 某科技攻关青年团队共有10人,其年龄(单位:岁)分布如下表所示,则这10个人年龄的 ( )
年龄 45 40 36 32 29 28
人数 1 2 1 3 2 1
A.中位数是34
B.众数是32
C.第25百分位数是29
D.平均数为34.3
9.(多选题)某城市在创建文明城市的活动中,为了解居民对“创建文明城市”的满意程度,组织居民给活动打分(分数为整数,满分100分),从中随机抽取一个样本容量为100的样本,发现分数均在[40,100]内.现将这些分数分成6组并画出样本的频率分布直方图,但不小心污损了部分图形,如图所示,则下列说法正确的是 ( )
A.频率分布直方图中第三组的频数为15
B.估计样本的众数为75分
C.估计样本的中位数为74分
D.估计样本的平均数为73分
二、填空题
10.10名学生进行1分钟跳绳比赛,他们的成绩数据分别为65,67,64,60,65,67,67,66,64,62,则这组数据的众数为 .
11.[2024·广东深圳中学高一期末] 某班有50名同学,一次数学测试的平均成绩是92分,如果30名男生的平均成绩为90分,那么20名女生的平均成绩为 分.
12.对一批底部周长在[80,130](单位:cm)内的树木进行研究,从中随机抽出200株树木并测出其底部周长,得到的频率分布直方图如图所示.由此估计,这批树木的底部周长的众数是 cm,中位数是 cm.
三、解答题
13.从某校高一年级新生中随机抽取一个容量为20的身高样本,数据如下(单位:cm,数据间无大小顺序要求):152,155,158,164,164,165,165,165,166,167,168,168,169,170,170,170,171,x,174,175.
(1)若x为这组数据的一个众数,求x的取值集合;
(2)若将样本数据按从小到大的顺序排列,第90百分位数是173,求x的值;
(3)若x=174,试估计该校高一年级新生的平均身高.
14.果切是一种新型水果售卖方式,商家通过对整果进行消洗、去皮、去核、冷藏等操作后,包装组合销售.
(1)统计得到10名果切消费者每周购买果切的次数依次为1,7,4,7,4,6,6,3,7,5,求这10个数据的平均数与方差s2.
(2)统计600名果切消费者的年龄,他们的年龄均在5岁到55岁之间,将所得数据按照[5,15),[15,25),[25,35),[35,45),[45,55]分组,得到的频率分布直方图如图.
①求这600名果切消费者中年龄不低于35岁的人数;
②估计这600名果切消费者年龄的中位数a及平均数(结果保留整数).
15.某工厂生产销售了30双皮鞋,其中各种尺寸的销售量如下表所示:
鞋的尺寸(cm) 22 22.5 23 23.5 24 24.5 25
销售量(双) 1 2 4 14 5 3 1
(1)这30双鞋尺寸的平均数为 ,中位数为 ,众数为 ;
(2)从实际出发,问题(1)中的众数对指导生产的意义是 .
16.[2024·重庆十八中高一月考] 2023年以来,某区把垃圾分类纳入积分,建立文明账户,市民以行动换积分,以积分转习惯.区政府为了了解4月份甲、乙两个社区居民换积分的情况,分别从甲、乙两个社区各抽取10人,记录下他们的积分(单位:分),并进行整理和分析(积分用x表示,共分为4组:A:x<70;B:70≤x<80,C:80≤x<90,D:90≤x≤100),下面给出了部分信息:
甲社区10人的积分:47,56,68,71,83,83,85,90,91,94;
乙社区10人的积分在C组中的积分为81,83,84,84.
乙社区10人的积分等级扇形图如图.
两组数据的平均数、中位数、众数如下表所示:
社区 平均数 中位数 众数
甲 76.8 83 b
乙 76.8 a 84
根据以上信息,解答下列问题.
(1)求a,b,m的值.
(2)根据以上数据,你认为哪个社区在此次垃圾分类换积分活动中表现更好 请说明理由(一条即可).
(3)若4月份甲社区有700人参与活动,乙社区有800人参与活动,用样本估计总体,估计4月份甲、乙两个社区积分在80分及以上的人数.
9.2.3 总体集中趋势的估计
1.A [解析] 众数是在一组数据中出现次数最多的数,所以一定会在原始数据中出现.
2.B [解析] 将这10位选手的得分从小到大排列为6,7,7,8,8,8,8,9,9,10,可知中位数为8,且8出现的次数最多,故众数为8.故选B.
3.D [解析] 由题意得=3,故x1+x2+x3+x4+x5=15,则===10.故选D.
4.C [解析] 若这100个数都是8,则这100个数据的中位数是8,故A错误;因为100为偶数,所以把这100个数据从小到大排列后,第50和第51个数据的平均数为中位数,故C正确,B,D错误.故选C.
5.A [解析] 众数是最高矩形的中点横坐标,因此众数在第二组的中点处.因为直方图在右边拖尾,所以平均数大于中位数,又中位数左边和右边的矩形面积之和相等,所以中位数在第二组右边,因此有众数<中位数<平均数.故选A.
6.D [解析] 由题意得(0.005+0.03+a+0.015)×10=1,解得a=0.05,因为0.05+0.3=0.35,0.05+0.3+0.5=0.85,0.35<0.75<0.85,所以样本数据的75%分位数x位于[80,90)内,则0.35+(x-80)×0.05=0.75,解得x=88.因为样本数据中位于[80,90)内的频率最大,所以众数y==85,故选D.
7.D [解析] 由4×(0.01+0.075+a+0.045+0.03+0.02+0.01)=1,可得a=0.06,所以S矩形ABCD=4×0.06=0.24,故A中说法正确;估计该市居民月均用水量的众数为=6(t),故B中说法正确;估计该市居民月均用水量不超过19 t的频率为4×(0.01+0.075+0.06+0.045)+×4×0.03=0.76+0.09=0.85,故C中说法正确;设这200户居民月均用水量的中位数为x1,因为第一个矩形的面积为0.04,第二个矩形的面积为0.3,第三个矩形的面积为0.24,所以中位数x1∈[8,12],由x1=8+×4=8+=,可估计这200户居民月均用水量的中位数为t,估计这200户居民月均用水量的平均数=4×0.01×2+4×0.075×6+4×0.06×10+4×0.045×14+4×0.03×18+4×0.02×22+4×0.01×26=11.76(t),因为<11<11.76,所以估计这200户居民月均用水量的中位数小于平均数,故D中说法不正确.故选D.
8.BCD [解析] 把这10个人的年龄从小到大排列为28,29,29,32,32,32,36,40,40,45,易知这组数据的中位数为32,众数为32,故A错误,B正确;由25%×10=2.5,得这组数据的第25百分位数是第3个数,为29,故C正确;这组数据的平均数==34.3,故D正确.故选BCD.
9.BD [解析] 对于A,因为分数在[60,70]内的频率为1-10×(0.005+0.020+0.030+0.025+0.010)=0.10,所以第三组的频数为100×0.10=10,故A错误;对于B,由图可估计样本的众数为75分,故B正确;对于C,因为10×(0.005+0.020+0.010)=0.35<0.5,10×(0.005+0.020+0.010+0.030)=0.65>0.5,所以中位数位于[70,80]内,设中位数为x,则0.35+0.03(x-70)=0.5,解得x=75,所以估计样本的中位数为75分,故C错误;对于D,估计样本的平均数为(45×0.005+55×0.020+65×0.010+75×0.030+85×0.025+95×0.010)×10=73(分),故D正确,故选BD.
10.67 [解析] 数据65,67,64,60,65,67,67,66,64,62中,出现次数最多的数据是67,即众数为67.
11.95 [解析] 设20名女生的平均成绩为,由题意得50×92=30×90+20×,解得=95(分).
12.105 [解析] 由题图,估计这批树木的底部周长的众数是=105(cm),中位数是+100=+100=(cm).
13.解:(1)若x为这组数据的一个众数,则x的可能取值为164,165,168,170,
即x的取值集合为{164,165,168,170}.
(2)因为样本数据的第90百分位数是173,且20×90%=18,
所以样本数据的第90百分位数为=173,
所以x=172.
(3)若x=174,则估计该校高一年级新生的平均身高为
×(152+155+158+164+164+165+165+165+166+167+168+168+169+170+170+170+171+174+174+175)=166.5(cm).
14.解:(1)==5,
s2=×[(1-5)2+(3-5)2+2×(4-5)2+(5-5)2+2×(6-5)2+3×(7-5)2]=3.6.
(2)①这600名果切消费者中年龄不低于35岁的人数为(0.015+0.005)×10×600=120.
②由0.020×10=0.2<0.5,(0.020+0.035)×10=0.55>0.5,可得15
估计这600名果切消费者年龄的平均数=10×0.020×10+20×0.035×10+30×0.025×10+40×0.015×10+50×0.005×10=25(岁).
15.(1)23.55 cm 23.5 cm 23.5 cm (2)尺寸为23.5 cm的鞋销量最好,厂家应多生产 [解析] (1)30双鞋尺寸的平均数=×(22×1+22.5×2+23×4+23.5×14+24×5+24.5×3+25×1)=23.55(cm).由于尺寸小于23.5 cm的销售量为1+2+4=7(双),尺寸大于23.5 cm的销售量为5+3+1=9(双),故将30个数据按从小到大的顺序排列,处于正中间位置的两个数据均为23.5,从而中位数为23.5 cm.因为数据23.5共出现14次,出现次数最多,所以众数也为23.5 cm.
(2)尺寸为23.5 cm的鞋销量最好,厂家应多生产.
16.解:(1)因为甲社区10人的积分中出现次数最多的数据为83,所以b=83.
由乙社区10人的积分等级扇形图可得,乙社区10人的积分在A组的人数为10×10%=1,在B组的人数为10×20%=2,因为乙社区10人的积分在C组中的积分为81,83,84,84,所以乙社区10人的积分从小到大排列后的第5和第6个数据分别为83,84,
所以a=×(83+84)=83.5.
因为乙社区10人的积分在D组的人数为10-1-2-4=3,所以D组人数所占的百分比为×100%=30%,所以m=30.
(2)乙社区在此次垃圾分类换积分活动中表现更好,理由如下:
因为虽然甲、乙两个社区积分的平均数相同,但是乙社区的中位数和众数均比甲社区高,所以乙社区在此次垃圾分类换积分活动中表现更好.
(3)在样本中,甲社区积分在80分及以上的人数所占的比例为=0.6,乙社区积分在80分及以上的人数所占的比例为=0.7,所以估计4月份甲、乙两个社区积分在80分及以上的人数为0.6×700+0.7×800=980.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
