(13) 三角形全等的判定—八年级数学华东师大版上册课前导学(含答案)
文档属性
| 名称 | (13) 三角形全等的判定—八年级数学华东师大版上册课前导学(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 666.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-11 21:56:53 | ||
图片预览

文档简介
(13) 三角形全等的判定—八年级数学华东师大版上册课前导学
一、知识预习
1.能够______________的两个三角形叫做全等三角形,把两个全等的三角形重合在一起,重合的顶点叫做_________,重合的边叫做__________,重合的角叫做_________
表示方法:和全等,记作________________,读作“三角形全等于三角形”
2.全等三角形的性质:_________相等,_________相等
3.三边分别相等的两个三角形 ,简写为 或 .
4.两角及其夹边分别相等的两个三角形全等,简写成 或 .
5.两角分别相等且其中一组等角的对边相等的两个三角形 ,简写成 或 .
6.两边及其夹角分别相等的两个三角形 ,简写成 或 .
7.斜边和一条 分别相等的两个三角形全等.简写成斜边、直角边”或“ ”.
二、自我检测
1.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A. B. C. D.和
2.如图所示,,,,的度数是( )
A.44° B.55° C.66° D.77°
3.如图,已知,则( )
A. B. C. D.不能确定
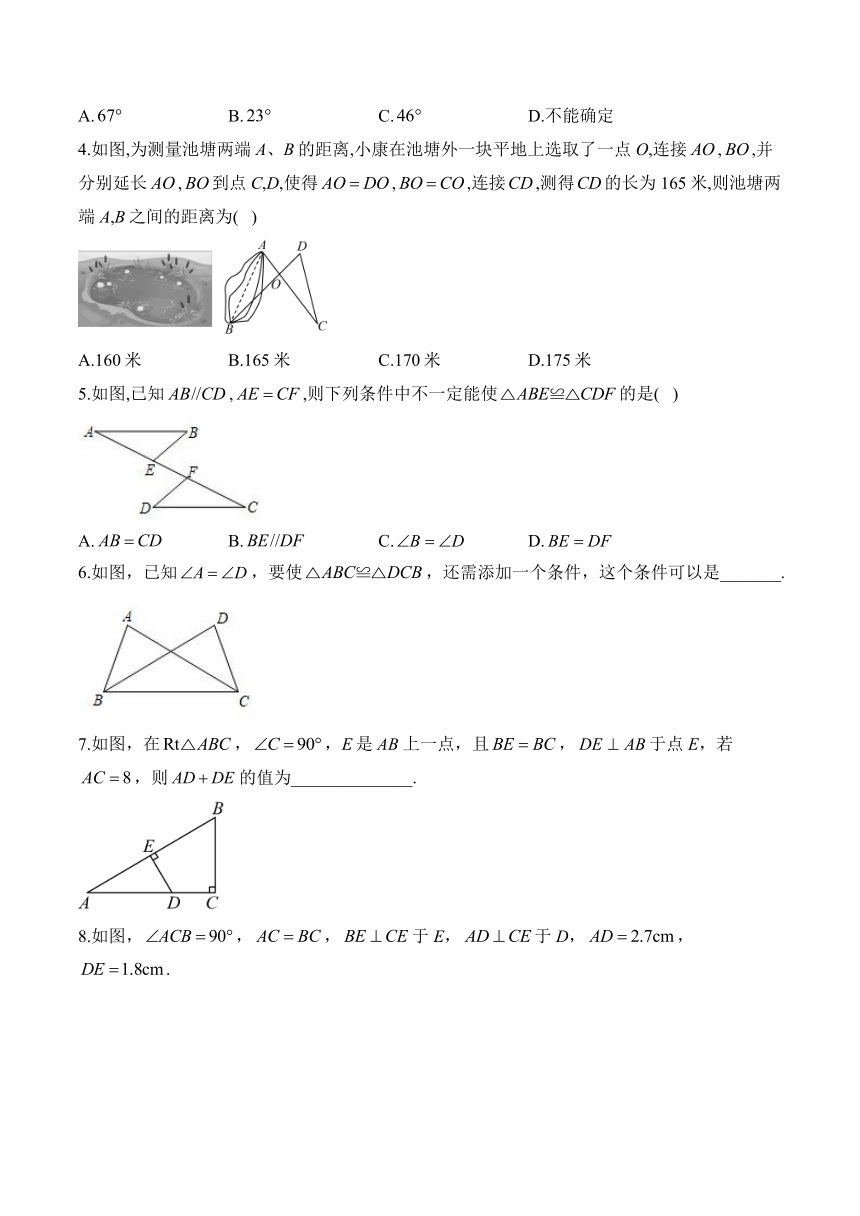
4.如图,为测量池塘两端A、B的距离,小康在池塘外一块平地上选取了一点O,连接,,并分别延长,到点C,D,使得,,连接,测得的长为165米,则池塘两端A,B之间的距离为( )
A.160米 B.165米 C.170米 D.175米
5.如图,已知,,则下列条件中不一定能使的是( )
A. B. C. D.
6.如图,已知,要使,还需添加一个条件,这个条件可以是_______.
7.如图,在,,E是上一点,且,于点E,若,则的值为______________.
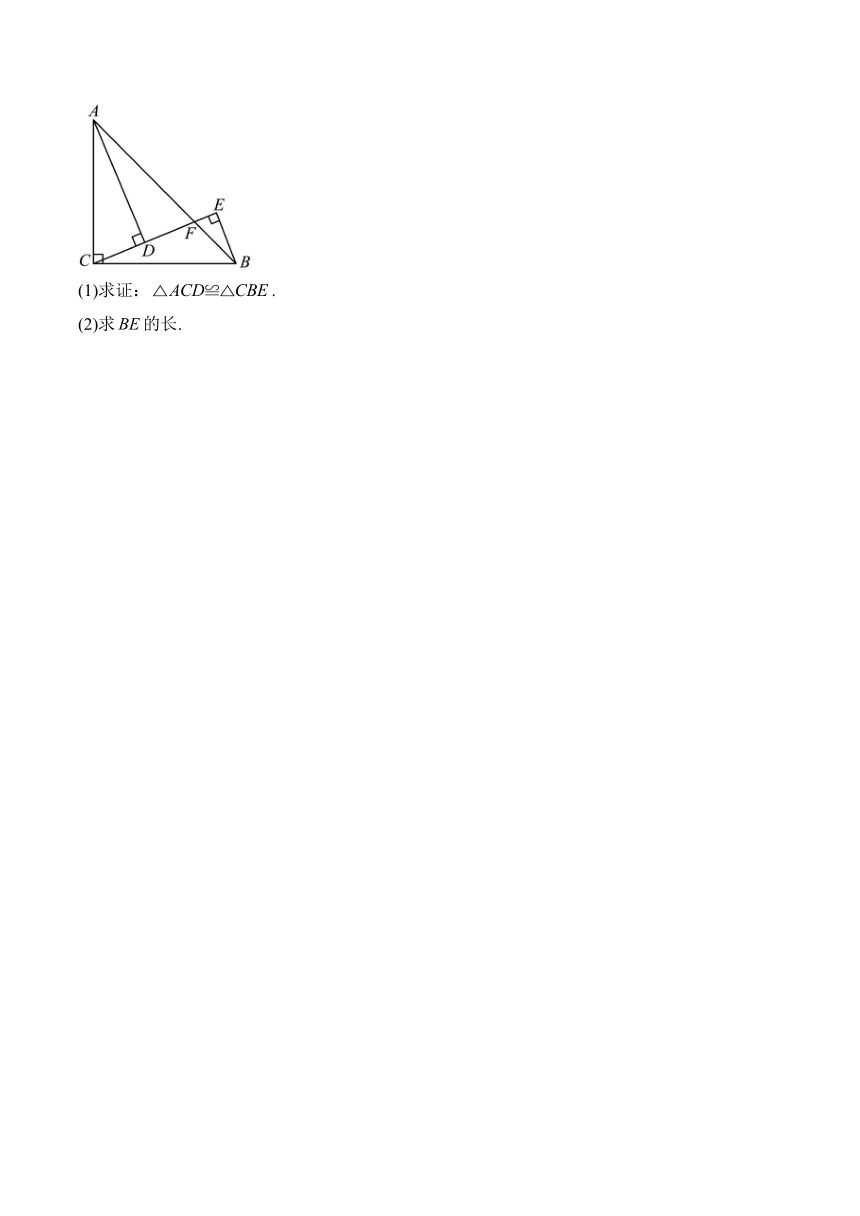
8.如图,,,于E,于D,,.
(1)求证:.
(2)求的长.
答案以及解析
一、知识预习
1.完全重合;对应顶点;对应边;对应角;
2.对应边;对应角
3.全等 边边边 SSS
4.角边角 ASA
5.全等 角角边 AAS
6.全等 边角边 SAS
7.直角边 HL
二、自我检测
1.答案:C
解析:A、第块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
B、第块,仅保留了原三角形的一部分边,所以该块不行;
C、第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合判定,符合题意;
D、由上分析,和不符合题意;
故选:C.
2.答案:B
解析:在中,,,
∴,
∵,
∴,
故选B.
3.答案:B
解析:连接,,,,,.
4.答案:B
解析:在和中
,
∴,
∴,
又米,
∴米.
故选∶B.
5.答案:D
解析:∵,
∴,
又∵,
∴(1)添加“”,可由“SAS”判定;
(2)添加“”可得,进一步可得,从而可由“ASA”判定;
(3)添加“”可由“AAS”判定;
(4)添加“”不能判定;
故选D.
6.答案:(答案不唯一)
解析:证明:若,
则在与中,
,
,
故答案为:(答案不唯一).
7.答案:8
解析:连接.
,,
与均是直角三角形.
,
,
,
.
故答案为:8.
8.答案:(1)见解析
(2)
解析:(1)证明:∵,,
∴,
∵,
∴,
∵,
∴,
在与中,,
∴;
(2)由(1)知,,
∴,,
∵,
∴.
一、知识预习
1.能够______________的两个三角形叫做全等三角形,把两个全等的三角形重合在一起,重合的顶点叫做_________,重合的边叫做__________,重合的角叫做_________
表示方法:和全等,记作________________,读作“三角形全等于三角形”
2.全等三角形的性质:_________相等,_________相等
3.三边分别相等的两个三角形 ,简写为 或 .
4.两角及其夹边分别相等的两个三角形全等,简写成 或 .
5.两角分别相等且其中一组等角的对边相等的两个三角形 ,简写成 或 .
6.两边及其夹角分别相等的两个三角形 ,简写成 或 .
7.斜边和一条 分别相等的两个三角形全等.简写成斜边、直角边”或“ ”.
二、自我检测
1.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A. B. C. D.和
2.如图所示,,,,的度数是( )
A.44° B.55° C.66° D.77°
3.如图,已知,则( )
A. B. C. D.不能确定
4.如图,为测量池塘两端A、B的距离,小康在池塘外一块平地上选取了一点O,连接,,并分别延长,到点C,D,使得,,连接,测得的长为165米,则池塘两端A,B之间的距离为( )
A.160米 B.165米 C.170米 D.175米
5.如图,已知,,则下列条件中不一定能使的是( )
A. B. C. D.
6.如图,已知,要使,还需添加一个条件,这个条件可以是_______.
7.如图,在,,E是上一点,且,于点E,若,则的值为______________.
8.如图,,,于E,于D,,.
(1)求证:.
(2)求的长.
答案以及解析
一、知识预习
1.完全重合;对应顶点;对应边;对应角;
2.对应边;对应角
3.全等 边边边 SSS
4.角边角 ASA
5.全等 角角边 AAS
6.全等 边角边 SAS
7.直角边 HL
二、自我检测
1.答案:C
解析:A、第块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
B、第块,仅保留了原三角形的一部分边,所以该块不行;
C、第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合判定,符合题意;
D、由上分析,和不符合题意;
故选:C.
2.答案:B
解析:在中,,,
∴,
∵,
∴,
故选B.
3.答案:B
解析:连接,,,,,.
4.答案:B
解析:在和中
,
∴,
∴,
又米,
∴米.
故选∶B.
5.答案:D
解析:∵,
∴,
又∵,
∴(1)添加“”,可由“SAS”判定;
(2)添加“”可得,进一步可得,从而可由“ASA”判定;
(3)添加“”可由“AAS”判定;
(4)添加“”不能判定;
故选D.
6.答案:(答案不唯一)
解析:证明:若,
则在与中,
,
,
故答案为:(答案不唯一).
7.答案:8
解析:连接.
,,
与均是直角三角形.
,
,
,
.
故答案为:8.
8.答案:(1)见解析
(2)
解析:(1)证明:∵,,
∴,
∵,
∴,
∵,
∴,
在与中,,
∴;
(2)由(1)知,,
∴,,
∵,
∴.
