山东省巨野县第一中学人教A版高中数学必修二《第一章 空间几何体》复习课件(共61张PPT)
文档属性
| 名称 | 山东省巨野县第一中学人教A版高中数学必修二《第一章 空间几何体》复习课件(共61张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 887.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-19 19:37:54 | ||
图片预览



文档简介
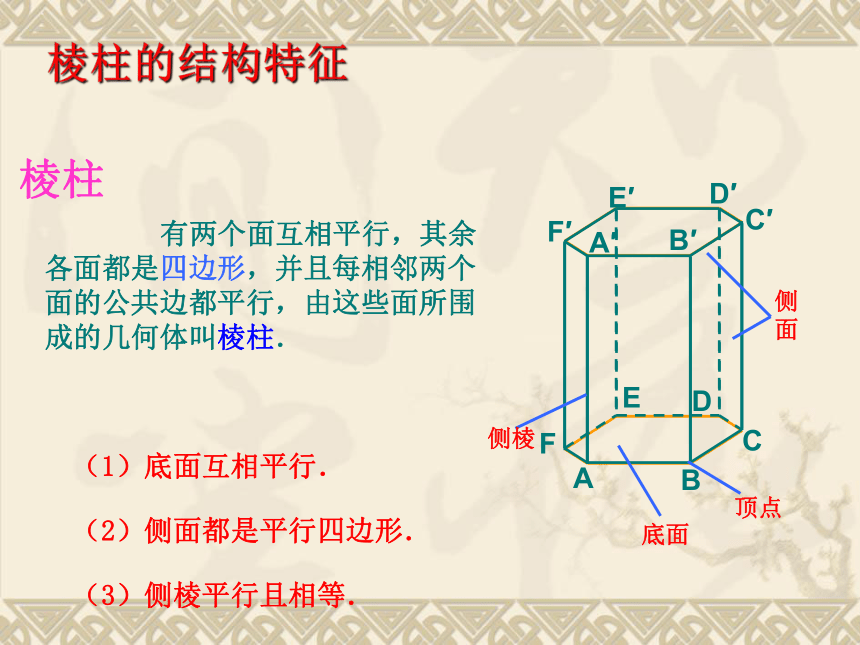
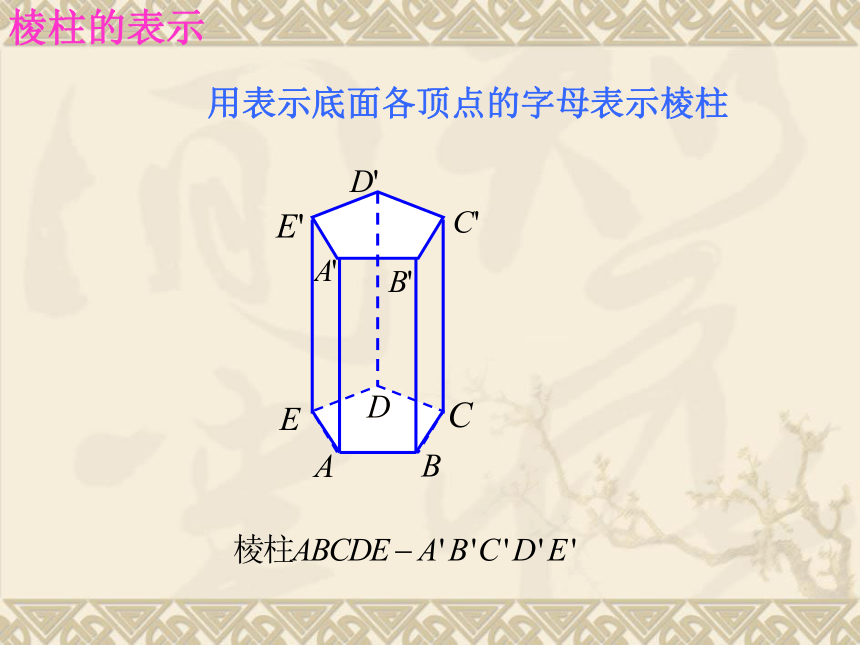
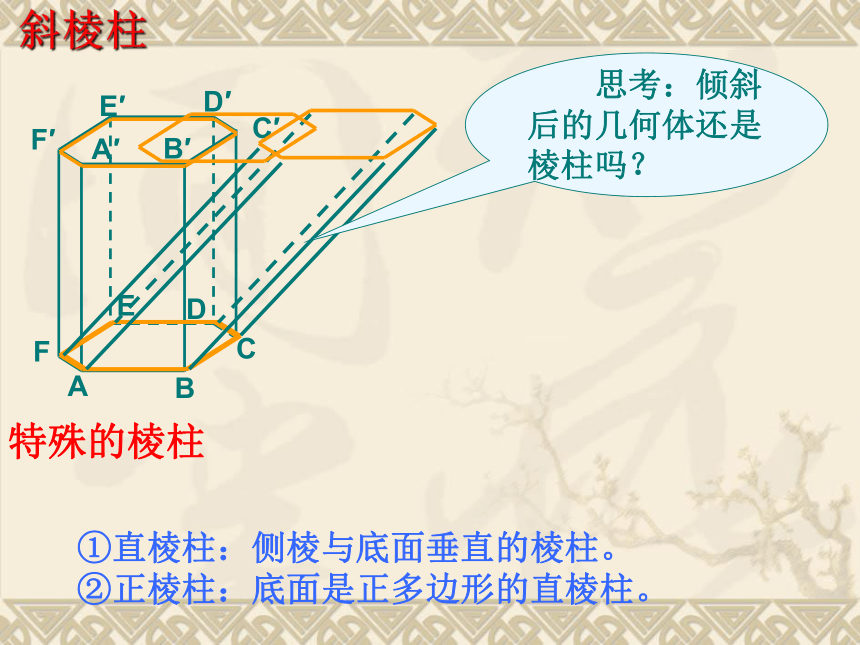
课件61张PPT。1.1.1柱、锥、台和球的结构特征 棱柱 有两个面互相平行,其余各面都是四边形,并且每相邻两个面的公共边都平行,由这些面所围成的几何体叫棱柱.(1)底面互相平行.棱柱的结构特征(2)侧面都是平行四边形.(3)侧棱平行且相等.棱柱的表示用表示底面各顶点的字母表示棱柱 思考:倾斜后的几何体还是棱柱吗?斜棱柱特殊的棱柱①直棱柱:侧棱与底面垂直的棱柱。
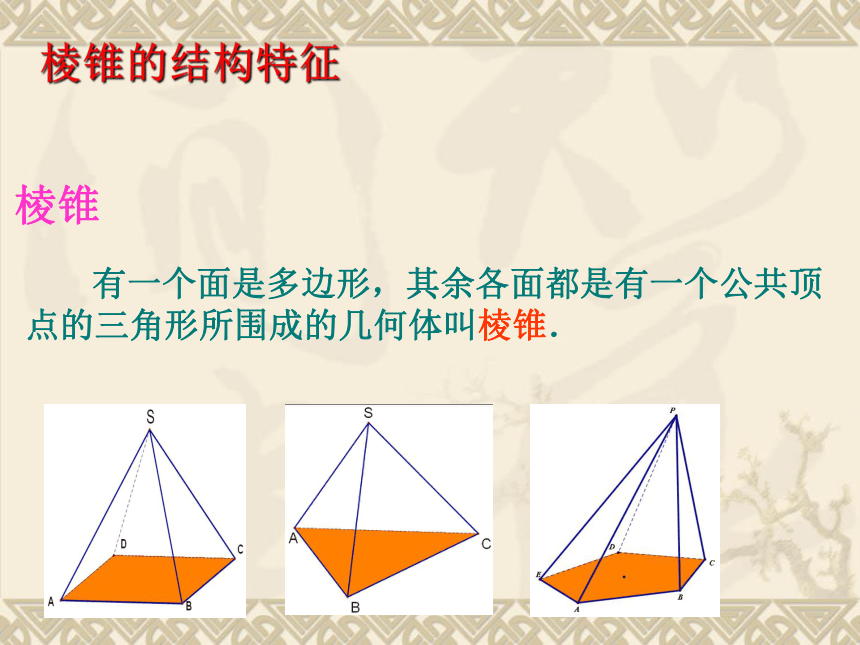
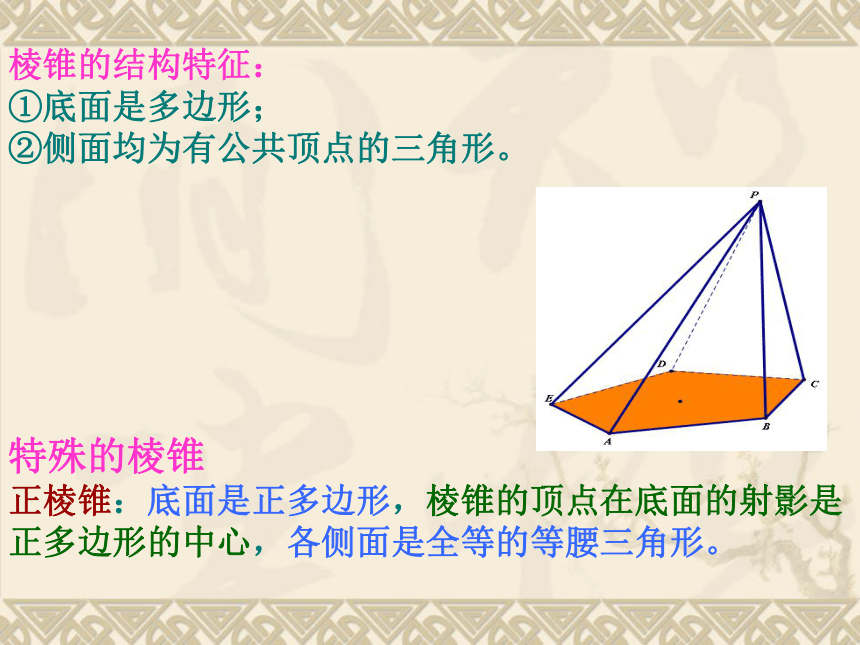
②正棱柱:底面是正多边形的直棱柱。 有一个面是多边形,其余各面都是有一个公共顶点的三角形所围成的几何体叫棱锥.棱锥的结构特征棱锥棱锥的结构特征:
①底面是多边形;
②侧面均为有公共顶点的三角形。特殊的棱锥
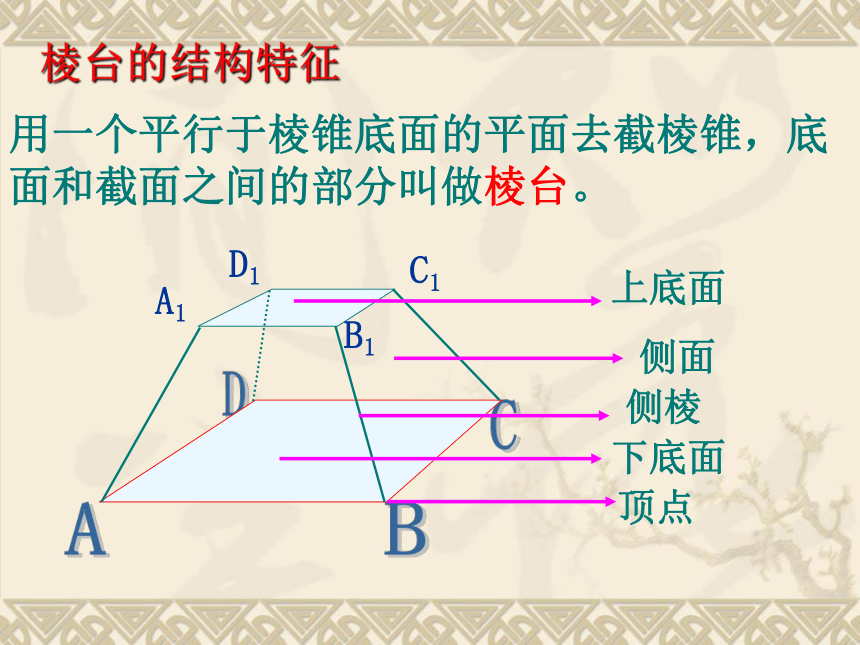
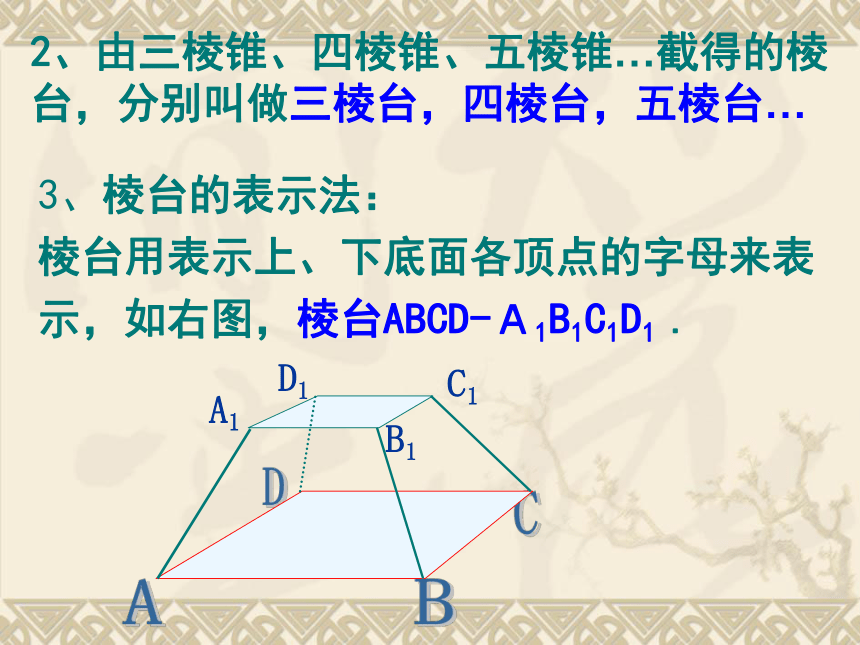
正棱锥:底面是正多边形,棱锥的顶点在底面的射影是正多边形的中心,各侧面是全等的等腰三角形。用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。DBCAC1 B1A1D1棱台的结构特征2、由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…3、棱台的表示法:
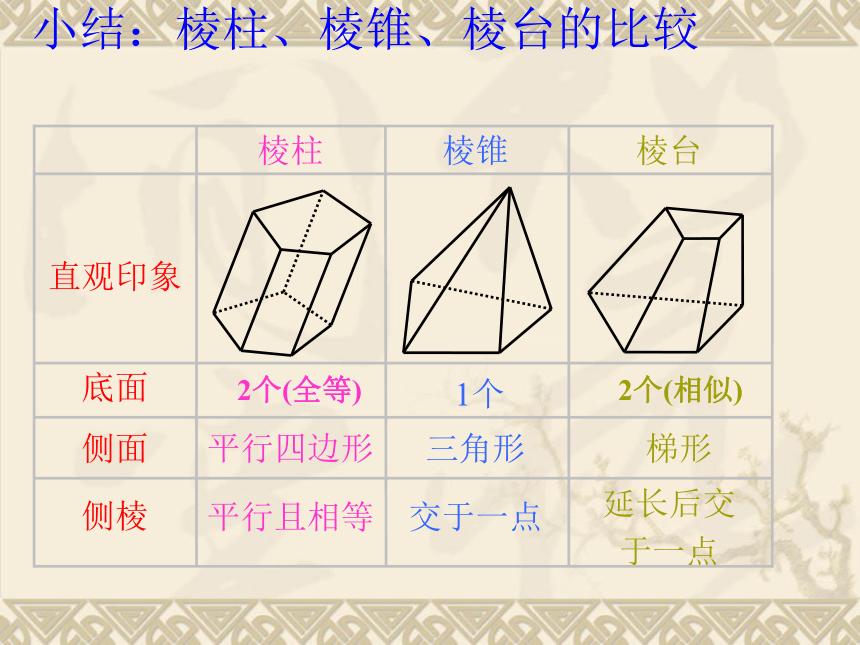
棱台用表示上、下底面各顶点的字母来表示,如右图,棱台ABCD-A1B1C1D1 .DBCAC1 B1A1D1小结:棱柱、棱锥、棱台的比较延长后交
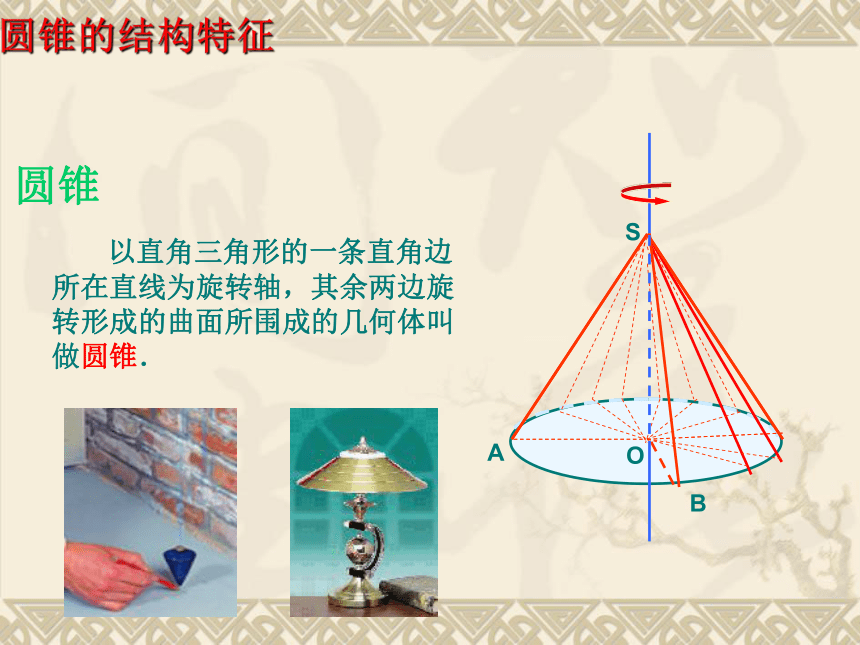
于一点交于一点平行且相等侧棱梯形三角形平行四边形侧面1个底面直观印象棱台棱锥棱柱2个(全等)2个(相似) 以矩形的一边所在直线为旋转轴,其余边旋转形成的曲面所围成的几何体叫做圆柱.圆柱圆柱的结构特征AB 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥.圆锥的结构特征圆锥 用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.圆台锥
体柱
体台
体柱、锥、台体的关系 棱柱、棱锥、棱台之间有什么关系?圆柱、圆锥、圆台之间呢?柱、锥、台体之间有什么关系?从旋转的角度分析,球是由什么图形绕哪条直线旋转而成的?以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球.几何体的分类柱体锥体台体球多面体旋转体知识探究(二):简单组合体的结构特征 现实世界中几何体的形状各种各样,除了柱体、锥体、台体和球体等简单几何体外,还有大量的几何体是由这些简单几何体组合而成的,这些几何体叫做简单组合体.例3 将下列平面图形绕直线AB旋转一周,所得的几何体分别是什么?理论迁移1.2.1空间几何体的三视图DCB一、中心投影:投射线投影面把光由一点向外散射形成的投影叫做中心投影。特点:中心投影的投影大小与物体和投影面之间的距离有关。二、平行投影:当把投影中心移到无穷远,在一束平行光线照射下形成的投影,叫做平行投影。二、平行投影:正投影:投影方向垂直于投影面
的投影。二、平行投影:斜投影:投影方向与投影面倾斜
的投影。什么是空间图形的三视图呢?我们从不同的方向观察同一物体时,
可能看到不同的图形。
从正面看到的图叫做正视图,
从左面看到的图叫做侧视图,
从上面看到的图叫做俯视图。三视图的作图步骤:侧视图 正视图 正视图方向俯视图方向侧视图方向1.确定三视图方向;2.先画出能反映物体真实形状的一个视图(一般为正视图); 3.布置视图位置:
正视图,侧视图,俯视图要求:俯视图安排在正视图的正下方,侧视图安排在正视图的正右方。 4.画图原则:长对正,高平齐,宽相等正视图方向侧视图方向俯视图方向长高宽 画一个物体的
三视图时,正视图,
侧视图,俯视图所
画的位置如图所示,且要符合如下原则:宽相等长对正高平齐正视图侧视图俯视图正侧俯正方体的三视图:长方体的三视图:正侧俯正侧俯圆柱的三视图:圆锥的三视图:正侧俯球的三视图:正侧俯棱柱的三视图:正侧俯棱锥的三视图:正侧俯棱锥的三视图:正侧俯棱台的三视图:正侧俯圆台的三视图:圆台的三视图:正侧俯圆台的三视图:正侧俯简单组合体的三视图注意:不可见的轮廓线,用虚线画出. 简单组合体的三视图思考ACBD下图中的三视图表示下面哪个几何体?俯视图侧视图正视图1.2.2空间几何体的直观图例1.用斜二测画法画水平放置的六边形的直观图(1)在已知图形中取互相垂直的x 轴和y 轴,两轴相交于O点.画直观图时,把它画成对应的 轴、
轴,使 ,它确定的平面表示水平平面.
(2)已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x′轴或y′轴的线段.
(3)已知图形中平行于x 轴的线段,在直观图中保持原长度不变;平行于y 轴的线段,长度为原来的一半.斜二测画法的步骤:(平面图形)C1.3.1柱、锥、台的表面积与体积正棱柱的侧面展开图棱柱的展开图S表=S底+S侧一、棱柱、棱锥、棱台的展开图及表面积的求法:棱锥的侧面展开图是什么?如何计算它的表面积?正棱锥的侧面展开图棱锥的展开图侧面展开S表=S底+S侧棱台的侧面展开图是什么?如何计算它的表面积?正棱台的侧面展开图棱台的展开图侧面展开S表=S底+S侧圆柱的侧面展开图是矩形二、圆柱、圆锥、圆台的展开图及表面积的求法:圆柱的展开图圆锥的侧面展开图是扇形圆锥的展开图圆台的侧面展开图是扇环圆台的展开图以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为:三、柱体、椎体、台体的体积的求法:棱台(圆台)的体积公式:1.3.2球的表面积与体积一、球的体积:设球的半径为R,它的体积只与半径R有关,是以R为自变量的函数。事实上,如果球的半径为R,那么它的体积二、球的表面积:S=4πR2设球的半径为R,它的表面积由半径R唯一确定,即它的表面积S也是以R为自变量的函数。事实上,如果球的半径为R,那么它的表面积82.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比_________.1.球的直径伸长为原来的2倍,体积变为原来的_倍.练习1:探究:若正方体的棱长为a,则:
(1)正方体的内切球的直径=
(2)正方体的外接球的直径=
(3)与正方体所有的棱相切的球的直径=
②正棱柱:底面是正多边形的直棱柱。 有一个面是多边形,其余各面都是有一个公共顶点的三角形所围成的几何体叫棱锥.棱锥的结构特征棱锥棱锥的结构特征:
①底面是多边形;
②侧面均为有公共顶点的三角形。特殊的棱锥
正棱锥:底面是正多边形,棱锥的顶点在底面的射影是正多边形的中心,各侧面是全等的等腰三角形。用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。DBCAC1 B1A1D1棱台的结构特征2、由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…3、棱台的表示法:
棱台用表示上、下底面各顶点的字母来表示,如右图,棱台ABCD-A1B1C1D1 .DBCAC1 B1A1D1小结:棱柱、棱锥、棱台的比较延长后交
于一点交于一点平行且相等侧棱梯形三角形平行四边形侧面1个底面直观印象棱台棱锥棱柱2个(全等)2个(相似) 以矩形的一边所在直线为旋转轴,其余边旋转形成的曲面所围成的几何体叫做圆柱.圆柱圆柱的结构特征AB 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥.圆锥的结构特征圆锥 用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.圆台锥
体柱
体台
体柱、锥、台体的关系 棱柱、棱锥、棱台之间有什么关系?圆柱、圆锥、圆台之间呢?柱、锥、台体之间有什么关系?从旋转的角度分析,球是由什么图形绕哪条直线旋转而成的?以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球.几何体的分类柱体锥体台体球多面体旋转体知识探究(二):简单组合体的结构特征 现实世界中几何体的形状各种各样,除了柱体、锥体、台体和球体等简单几何体外,还有大量的几何体是由这些简单几何体组合而成的,这些几何体叫做简单组合体.例3 将下列平面图形绕直线AB旋转一周,所得的几何体分别是什么?理论迁移1.2.1空间几何体的三视图DCB一、中心投影:投射线投影面把光由一点向外散射形成的投影叫做中心投影。特点:中心投影的投影大小与物体和投影面之间的距离有关。二、平行投影:当把投影中心移到无穷远,在一束平行光线照射下形成的投影,叫做平行投影。二、平行投影:正投影:投影方向垂直于投影面
的投影。二、平行投影:斜投影:投影方向与投影面倾斜
的投影。什么是空间图形的三视图呢?我们从不同的方向观察同一物体时,
可能看到不同的图形。
从正面看到的图叫做正视图,
从左面看到的图叫做侧视图,
从上面看到的图叫做俯视图。三视图的作图步骤:侧视图 正视图 正视图方向俯视图方向侧视图方向1.确定三视图方向;2.先画出能反映物体真实形状的一个视图(一般为正视图); 3.布置视图位置:
正视图,侧视图,俯视图要求:俯视图安排在正视图的正下方,侧视图安排在正视图的正右方。 4.画图原则:长对正,高平齐,宽相等正视图方向侧视图方向俯视图方向长高宽 画一个物体的
三视图时,正视图,
侧视图,俯视图所
画的位置如图所示,且要符合如下原则:宽相等长对正高平齐正视图侧视图俯视图正侧俯正方体的三视图:长方体的三视图:正侧俯正侧俯圆柱的三视图:圆锥的三视图:正侧俯球的三视图:正侧俯棱柱的三视图:正侧俯棱锥的三视图:正侧俯棱锥的三视图:正侧俯棱台的三视图:正侧俯圆台的三视图:圆台的三视图:正侧俯圆台的三视图:正侧俯简单组合体的三视图注意:不可见的轮廓线,用虚线画出. 简单组合体的三视图思考ACBD下图中的三视图表示下面哪个几何体?俯视图侧视图正视图1.2.2空间几何体的直观图例1.用斜二测画法画水平放置的六边形的直观图(1)在已知图形中取互相垂直的x 轴和y 轴,两轴相交于O点.画直观图时,把它画成对应的 轴、
轴,使 ,它确定的平面表示水平平面.
(2)已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x′轴或y′轴的线段.
(3)已知图形中平行于x 轴的线段,在直观图中保持原长度不变;平行于y 轴的线段,长度为原来的一半.斜二测画法的步骤:(平面图形)C1.3.1柱、锥、台的表面积与体积正棱柱的侧面展开图棱柱的展开图S表=S底+S侧一、棱柱、棱锥、棱台的展开图及表面积的求法:棱锥的侧面展开图是什么?如何计算它的表面积?正棱锥的侧面展开图棱锥的展开图侧面展开S表=S底+S侧棱台的侧面展开图是什么?如何计算它的表面积?正棱台的侧面展开图棱台的展开图侧面展开S表=S底+S侧圆柱的侧面展开图是矩形二、圆柱、圆锥、圆台的展开图及表面积的求法:圆柱的展开图圆锥的侧面展开图是扇形圆锥的展开图圆台的侧面展开图是扇环圆台的展开图以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为:三、柱体、椎体、台体的体积的求法:棱台(圆台)的体积公式:1.3.2球的表面积与体积一、球的体积:设球的半径为R,它的体积只与半径R有关,是以R为自变量的函数。事实上,如果球的半径为R,那么它的体积二、球的表面积:S=4πR2设球的半径为R,它的表面积由半径R唯一确定,即它的表面积S也是以R为自变量的函数。事实上,如果球的半径为R,那么它的表面积82.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比_________.1.球的直径伸长为原来的2倍,体积变为原来的_倍.练习1:探究:若正方体的棱长为a,则:
(1)正方体的内切球的直径=
(2)正方体的外接球的直径=
(3)与正方体所有的棱相切的球的直径=
