山东省巨野县第一中学人教A版高中数学必修三《2.2.2 用样本数字特征估计总体数字特征》课件(共21张PPT)
文档属性
| 名称 | 山东省巨野县第一中学人教A版高中数学必修三《2.2.2 用样本数字特征估计总体数字特征》课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 504.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-19 19:50:44 | ||
图片预览






文档简介
课件21张PPT。用样本的数字特征估计总体的数字特征(众数、中位数、平均数、标准差)三数概念1、众数 在一组数据中,出现次数最多的数据叫做这一组数据的众数。2、中位数 将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数。3、平均数 一组数据的总和除以数据的个数所得的值。求下面这组数据的众数、中位数、平均数众数为6 中位数为6 平均数
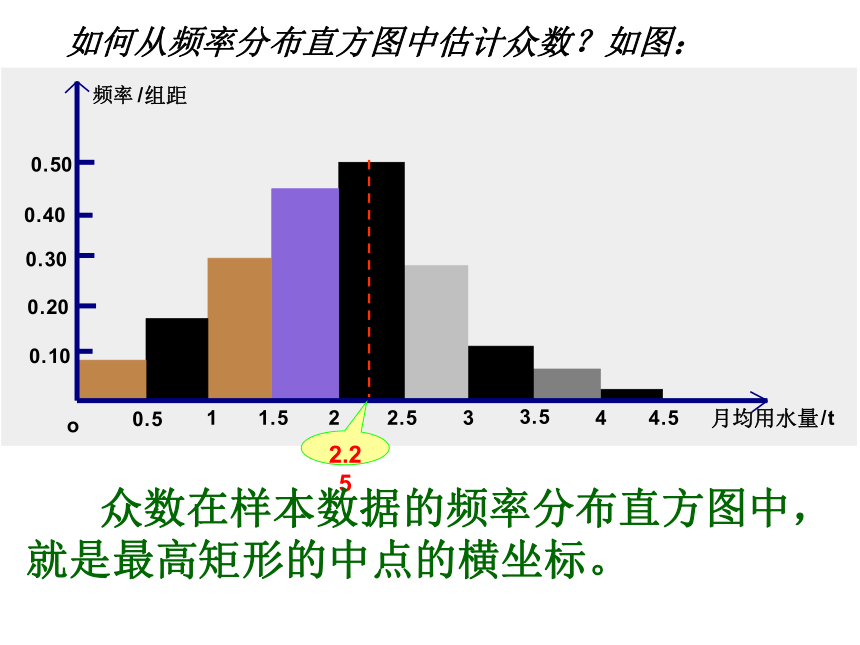
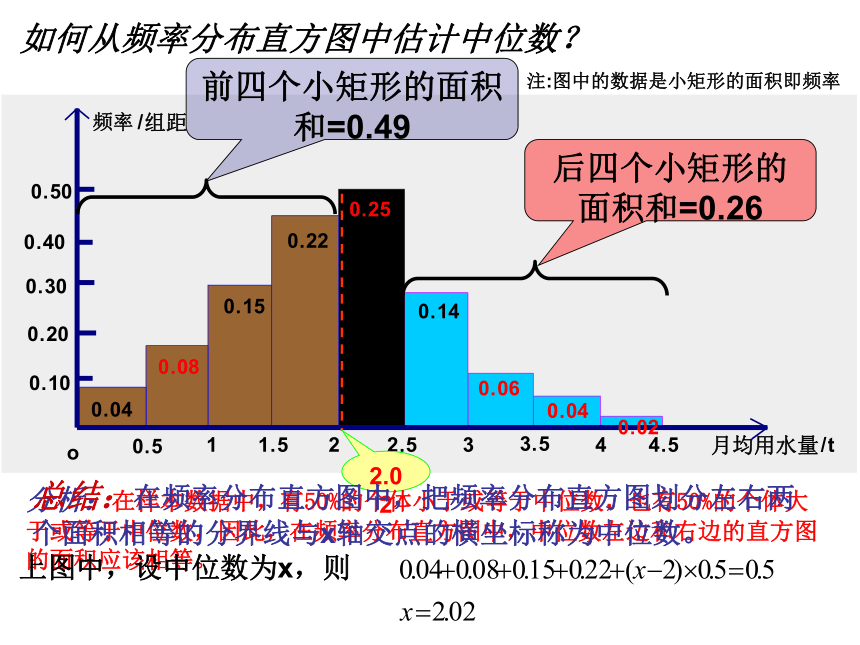
也可以说平均数为各个不同数字乘以相应频率之和。4、4、4、6、6、6、6、8、8、8如何从频率分布直方图中估计众数?如图:2.25 众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。思考:频率分布直方图中估计的众数与原始数据中的众数2.3不同,为什么? 在频率分布直方图,我们只能直观地看出数据的大概分布情况,从直方图本身得不出原始的数据内容,直方图已经损失一些样本信息。讨论:众数估计总体情况有什么优缺点? 能够体现样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征。如何从频率分布直方图中估计中位数? 前四个小矩形的面积和=0.492.02后四个小矩形的面积和=0.26分析:在样本数据中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等。 总结:在频率分布直方图中,把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标称为中位数。 注:图中的数据是小矩形的面积即频率
上图中,设中位数为x,则
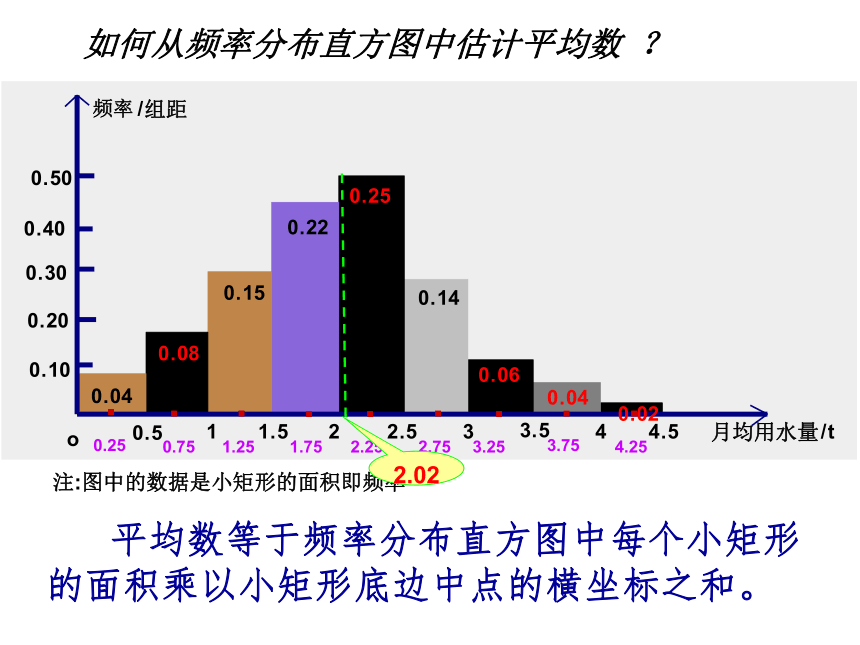
思考:2.02这个中位数的估计值,与样本数据的中位数2.0不同,为什么? 从频率分布直方图本身得不出原始的数据内容,频率分布直方图已经损失一些样本信息。思考:中位数不受少数极端值的影响,这在某些情 况下是一个优点,但它对极端值的不敏感有时也会成为缺点,你能举例说明吗? 考察100位居民的月均用水量表中的数据,如果把最后一个数据错写成22,并不会对样本中位数产生影响也就是说对极端数据不敏感的方法能够有效地预防错误数据的影响,而在实际应用中人为操作的失误经常造成错误数据。对极端值不敏感有利的例子: 某人具有初级计算机专业技术水平,想找一份收入好的工作。这时如果采用各个公司计算机专业技术人员收入的中位数作为选择工作的参考指标就会冒这样的风险:很可能所选择公司的初级计算机专业技术水平人员的收入很低,其原因是中位数对极小的数据不敏感。这里更好的方法是同时用平均数和中位数来作为参考指标,选择平均数较大且中位数较大的公司就业。对极端值不敏感有弊的例子: 如何从频率分布直方图中估计平均数 ? 注:图中的数据是小矩形的面积即频率
平均数等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。2.02思考:平均数估计总体情况有什么优缺点? 平均数与每一个样本的数据有关,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。想一想:某次数学期中考试,毛毛同学得了78分。全班共30人,其他同学的成绩为1个100分, 4个90分, 22个80分, 以及一个2分和一个10分。毛毛计算出全班的平均分为77分,所以毛毛回家告诉妈妈说,他这次成绩处于班级“中上水平”。这种说法对吗?2.标准差 平均数向我们提供了样本数据的重要信息,但是平均有时也会使我们作出对总体的片面判断.因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽略的.因此,只有平均数还难以概括样本数据的实际状态. 例如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:甲:7 8 7 9 5 4 9 10 7 4乙:9 5 7 8 7 6 8 6 7 7如果你是教练,你应当如何对这次射击作出评价?如果看两人本次射击的平均成绩,由于 两人射击 的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
有两位射击运动员在一次射击测试中各射靶十次,每次命中的环数如下: 如果你是教练,你应当如何对这次射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择? 直观上看,还是有差异的.如:甲成绩比较分散,乙成绩相对集中. 考察样本数据的分散程度的大小,最常用的统计量是标准差.标准差是样本数据到平均数的一种平均距离,一般用s表示. 例题1:画出下列四组样本数据的条形图,说明它们的异同点.解:四组样本数据的条形图是:四组数据的平均数都是5.0,标准差分别是0.00,0.82,1.49,2.83.虽然它们有相同的平均数,但是它们有不同的标准差,说明数据的分散程度是不一样的. 例2、甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm)甲 25.46, 25.32, 25.45, 25.39, 25.36
25.34, 25.42, 25.45, 25.38, 25.42
25.39, 25.43, 25.39, 25.40, 25.44
25.40, 25.42, 25.35, 25.41, 25.39乙 25.40, 25.43, 25.44, 25.48, 25.48
25.47, 25.49, 25.49, 25.36, 25.34
25.33, 25.43, 25.43, 25.32, 25.47
25.31, 25.32, 25.32, 25.32, 25.48 从生产的零件内径的尺寸看,谁生产的质量较高?分析 每一个工人生产的所有零件的内径尺寸组成一个总体,由于零件的生产标准已经给出(内径25.40mm),生产质量可以从总体的平均数与标准差两个角度来衡量.总体的平均数与内径标准尺寸25.00mm的差异大时质量低,差异小时质量高;当总体的平均数与标准尺寸很接近时,总体的标准差小的时候质量高,标准差大的时候质量低.这样比较两人的生产质量只要比较他们所生产的零件内径尺寸所组成的两个总体的平均数与标准差的大小即可.但是这两个总体的平均数与标准差都是不知道的,根据用样本估计总体的思想,我们可以通过抽样分别获得相应的样体数据,然后比较这两个样本的平均数,标准差,以此作为两个总体之间的估计值.解:用计算器计算可得: 1.农场种植的甲乙两种水稻,在面积相等的两块稻田中连续6年的平均产量如下(单位是:500g):品种 第1年 第2 年 第3年 第四年 第5年 第6年甲 900 920 900 850 910 920乙 890 960 950 850 860 890解: 依题意计算可得
=900 =900
s1≈23.8 s2 ≈42.6
甲乙两种水稻6年平均产量的平均数相同,但甲的标准差比乙的小,所以甲的生产比较稳定.
也可以说平均数为各个不同数字乘以相应频率之和。4、4、4、6、6、6、6、8、8、8如何从频率分布直方图中估计众数?如图:2.25 众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。思考:频率分布直方图中估计的众数与原始数据中的众数2.3不同,为什么? 在频率分布直方图,我们只能直观地看出数据的大概分布情况,从直方图本身得不出原始的数据内容,直方图已经损失一些样本信息。讨论:众数估计总体情况有什么优缺点? 能够体现样本数据的最大集中点,但它对其它数据信息的忽视使得无法客观地反映总体特征。如何从频率分布直方图中估计中位数? 前四个小矩形的面积和=0.492.02后四个小矩形的面积和=0.26分析:在样本数据中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等。 总结:在频率分布直方图中,把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标称为中位数。 注:图中的数据是小矩形的面积即频率
上图中,设中位数为x,则
思考:2.02这个中位数的估计值,与样本数据的中位数2.0不同,为什么? 从频率分布直方图本身得不出原始的数据内容,频率分布直方图已经损失一些样本信息。思考:中位数不受少数极端值的影响,这在某些情 况下是一个优点,但它对极端值的不敏感有时也会成为缺点,你能举例说明吗? 考察100位居民的月均用水量表中的数据,如果把最后一个数据错写成22,并不会对样本中位数产生影响也就是说对极端数据不敏感的方法能够有效地预防错误数据的影响,而在实际应用中人为操作的失误经常造成错误数据。对极端值不敏感有利的例子: 某人具有初级计算机专业技术水平,想找一份收入好的工作。这时如果采用各个公司计算机专业技术人员收入的中位数作为选择工作的参考指标就会冒这样的风险:很可能所选择公司的初级计算机专业技术水平人员的收入很低,其原因是中位数对极小的数据不敏感。这里更好的方法是同时用平均数和中位数来作为参考指标,选择平均数较大且中位数较大的公司就业。对极端值不敏感有弊的例子: 如何从频率分布直方图中估计平均数 ? 注:图中的数据是小矩形的面积即频率
平均数等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。2.02思考:平均数估计总体情况有什么优缺点? 平均数与每一个样本的数据有关,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计时可靠性降低。想一想:某次数学期中考试,毛毛同学得了78分。全班共30人,其他同学的成绩为1个100分, 4个90分, 22个80分, 以及一个2分和一个10分。毛毛计算出全班的平均分为77分,所以毛毛回家告诉妈妈说,他这次成绩处于班级“中上水平”。这种说法对吗?2.标准差 平均数向我们提供了样本数据的重要信息,但是平均有时也会使我们作出对总体的片面判断.因为这个平均数掩盖了一些极端的情况,而这些极端情况显然是不能忽略的.因此,只有平均数还难以概括样本数据的实际状态. 例如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:甲:7 8 7 9 5 4 9 10 7 4乙:9 5 7 8 7 6 8 6 7 7如果你是教练,你应当如何对这次射击作出评价?如果看两人本次射击的平均成绩,由于 两人射击 的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
有两位射击运动员在一次射击测试中各射靶十次,每次命中的环数如下: 如果你是教练,你应当如何对这次射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择? 直观上看,还是有差异的.如:甲成绩比较分散,乙成绩相对集中. 考察样本数据的分散程度的大小,最常用的统计量是标准差.标准差是样本数据到平均数的一种平均距离,一般用s表示. 例题1:画出下列四组样本数据的条形图,说明它们的异同点.解:四组样本数据的条形图是:四组数据的平均数都是5.0,标准差分别是0.00,0.82,1.49,2.83.虽然它们有相同的平均数,但是它们有不同的标准差,说明数据的分散程度是不一样的. 例2、甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm)甲 25.46, 25.32, 25.45, 25.39, 25.36
25.34, 25.42, 25.45, 25.38, 25.42
25.39, 25.43, 25.39, 25.40, 25.44
25.40, 25.42, 25.35, 25.41, 25.39乙 25.40, 25.43, 25.44, 25.48, 25.48
25.47, 25.49, 25.49, 25.36, 25.34
25.33, 25.43, 25.43, 25.32, 25.47
25.31, 25.32, 25.32, 25.32, 25.48 从生产的零件内径的尺寸看,谁生产的质量较高?分析 每一个工人生产的所有零件的内径尺寸组成一个总体,由于零件的生产标准已经给出(内径25.40mm),生产质量可以从总体的平均数与标准差两个角度来衡量.总体的平均数与内径标准尺寸25.00mm的差异大时质量低,差异小时质量高;当总体的平均数与标准尺寸很接近时,总体的标准差小的时候质量高,标准差大的时候质量低.这样比较两人的生产质量只要比较他们所生产的零件内径尺寸所组成的两个总体的平均数与标准差的大小即可.但是这两个总体的平均数与标准差都是不知道的,根据用样本估计总体的思想,我们可以通过抽样分别获得相应的样体数据,然后比较这两个样本的平均数,标准差,以此作为两个总体之间的估计值.解:用计算器计算可得: 1.农场种植的甲乙两种水稻,在面积相等的两块稻田中连续6年的平均产量如下(单位是:500g):品种 第1年 第2 年 第3年 第四年 第5年 第6年甲 900 920 900 850 910 920乙 890 960 950 850 860 890解: 依题意计算可得
=900 =900
s1≈23.8 s2 ≈42.6
甲乙两种水稻6年平均产量的平均数相同,但甲的标准差比乙的小,所以甲的生产比较稳定.
