山东省巨野县第一中学人教A版高中数学必修三《3.1 随机事件的概率》课件(共29张PPT)
文档属性
| 名称 | 山东省巨野县第一中学人教A版高中数学必修三《3.1 随机事件的概率》课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 419.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-19 19:51:59 | ||
图片预览








文档简介
课件29张PPT。3.1.1 随机事件的概率情境引入: 有两个箱子,一号箱子里有奖券100张,
其中一等奖1个;二号箱子里有奖券100张,
其中有一等奖10个。而每个箱子的一等奖的
奖品是一样的,那么,请同学们告诉我要取
得一等奖,你们会建议我到哪个箱子摸奖?如果二号箱子里有奖券1000张,一等奖还是
有10个,你们会建议我到哪个箱子去摸奖?考察下列事件能否发生?
(1)导体通电时发热;
(2)向上抛出的石头会下落;
(3)在标准大气压下水温升高到100°C会 沸腾.
必然发生必然发生必然发生必然事件:在一定条件下必然要发生的事件叫必然事件;知识探究:必然事件、不可能事件、随机事件
不可能发生不可能发生不可能发生不可能事件:在一定条件下不可能发生的事件叫不可能事件;考察下列事件能否发生?
(1)在没有水分的真空中种子发芽;
(2)在常温常压下钢铁融化;
(3).知识探究:必然事件、不可能事件、随机事件
可能发生也可能不发生可能发生也可能不发生可能发生也可能不发生考察下列事件能否发生?
(1)某人射击一次命中目标;
(2)马林能夺取北京奥运会男
子乒乓球单打冠军;
(3)抛掷一个骰字出现的点数为偶数. 随机事件:在一定条件下可能发生也可能不发生的事件叫随机事件。知识探究:必然事件、不可能事件、随机事件指出下列事件是必然事件,不可能事件,还是随机事件:随机事件必然事件不可能事件随机事件随机事件练习指出下列事件中,哪些是不可能事件?哪些是必然事件?哪些是随机事件?
(1)若a、b、c都是实数,则a(bc)=(ab)c;
(2)没有空气,动物也能生存下去;
(3)在标准大气压下,水在温度90?C时沸腾;
(4)直线y=k(x+1)过定点(?1,0);
(5)某一天内电话收到的呼叫次数为0;
(6)一个袋内装有形状大小相同的一个白球和一个黑球,从中任意摸出1个球则为白球 必然事件不可能事件不可能事件必然事件随机事件随机事件思考解惑: 由于随机事件具有不确定性,因而从表
面看似乎偶然性在起支配作用,没有什么必
然性。但人们经过长期的实践并深入研究后,
发现随机事件虽然就每次试验结果来说,具
有不确定性,然而在大量重复实验中,它却
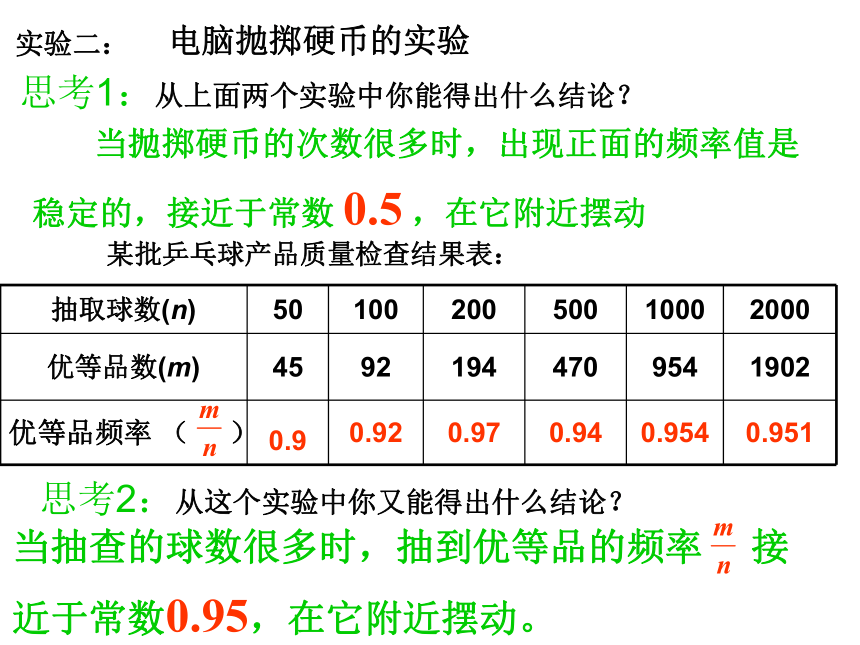
呈现出一种完全确定的规律性。下面请同学们来做抛掷硬币的实验: 实验一:频 数频 率 当抛掷硬币的次数很多时,出现正面的频率值是稳定的,接近于常数 0.5 ,在它附近摆动实验二:电脑抛掷硬币的实验 某批乒乓球产品质量检查结果表:当抽查的球数很多时,抽到优等品的频率 接近于常数0.95,在它附近摆动。思考1:从上面两个实验中你能得出什么结论?思考2:从这个实验中你又能得出什么结论?思考3:上述试验表明,随机事件在每次试验中是否发生是不能预知的,但是在大量重复试验后,随着试验次数的增加,事件A发生的频率呈现出一定的规律性,这个规律性是如何体现出来的? 事件发生的频率较稳定,在某个常数附近摆动. 思考4: 那么在上述抛掷硬币的试验中,正面向 上发生的概率是多少?思考5:在实际问题中,随机事件发生的概率往 往是未知的(如在一定条件下射击命中目标的概 率),你如何得到事件发生的概率? 通过大量重复试验得到事件A发生的频率的稳定值,即概率. 思考6:在相同条件下,事件A在先后两次试验中发生的频率是否一定相等?事件A在先后两次试验中发生的概率 P(A)是否一定相等? 频率具有随机性,做同样次数的重复试验,事件A发生的频率可能不相同;概率是一个确定的数,是客观存在的,与每次试验无关.思考7:必然事件、不可能事件发生的概率分别为多少?概率的取值范围是什么? 概率的性质:(1)求一个事件的概率的基本方法是通过大量的重复试验;
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A的概率;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5)必然事件的概率为1,不可能事件的概率为0.因此0?P(A)?1 1.抛掷100枚质地均匀的硬币,有下列一些说法:
①全部出现正面向上是不可能事件;
②至少有1枚出现正面向上是必然事件;
③出现50枚正面向上50枚正面向下是随机事件,
以上说法中正确说法的个数为 ( )
A.0个 B.1个 C.2个 D.3个 2.下列说法正确的是 ( )
A.任何事件的概率总是在(0,1)之间
B.频率是客观存在的,与试验次数无关
C.随着试验次数的增加,频率一般会越来越接近概率
D.概率是随机的,在试验前不能确定
练一练BC
1、本节需掌握的知识:
①了解必然事件,不可能事件,随机事件的概念;
②理解随机事件的发生在大量重复试验下,呈现规律性;
③理解概率的意义及其性质。
2、必然事件、不可能事件、随机事件是在一定的条件下发生的,当条件变化时,事件的性质也发生变化。
3、必然事件与不可能事件可看作随机事件的两种特殊情况.因此,任何事件发生的概率都满足:0≤P(A)≤1。
4、随机事件在相同的条件下进行大量的试验时,呈现规律性,且频率 总是接近于常数P(A),称P(A)为事件的概率。3.1.2 概率的意义1、概率的正确理解问题1:有人说,既然抛掷一枚硬币出现正面 的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上。 你认为这种想法正确吗?让事实说话! 让我们做一个抛掷硬币的试验,观察它落地时的情况。每人各取一枚同样的硬币,连续两次抛掷,观察它落地后的朝向,并记录下结果,填入下表。重复上面的过程10次,把全班同学试验结果汇总,计算三种结果发生的频率。问题2:有人说,中奖率为 的彩
票,买1000张一定中奖,这种理解对吗? 说明:虽然中奖张数是随机的,但这种随机性中具有规律性。随着试验次数的增加,即随着买的彩票张数的增加,大约有
的彩票中奖。实际上,买1000张彩票中奖的
概率为 。
没有一张中奖也是有可能的,其概率近似为0.3677。2.概率与公平性的关系问题3:你有没有注意到在乒乓球、排球等体育比赛中,如何确定由哪一方先发球?你觉得那些方法对比赛双方公平吗?3.概率与决策的关系问题4:在一次试验中,连续10次投掷一枚骰子,结果出现的都是1点,你认为这个骰子的质地均匀吗?为什么? 如果我们面临的是从多个可选答案中挑选正确答案的决策任务,那么“使得样本出现的可能性最大”可以作为决策的准则,这种判断问题的方法称为极大似然法。极大似然法是统计中重要的统计思想方法之一。如果我们的判断结论能够使得样本出现的可能性最大,那么判断正确的可能性也最大,这种判断问题的方法称为似然法。似然法是统计中重要的统计思想方法之一。通过刚学过的概率知识我们可以推断,如果它是均匀的,通过试验和观察,可以发现出现各个面的可能性都应该是 ,从而连续10次出现1点的概率为
,这在一次试验(即连续10次抛掷一枚骰子)中是几乎不可能发生的(在一次试验中几乎不可能发生的事件称为小概率事件)。4、天气预报的概率解释 某地气象局预报说,明天本地降水概率为70%。你认为下面两个解释哪一个能代表气象局的观点?
(1)明天本地有70%的区域下雨,30%的区域不下雨;
(2)明天本地下雨的机会是70%。 (1)显然是不正确的,因为70%的概率是说降水的概率,而不是说70%的区域降水。正确的选择是(2)。 降水概率的大小只能说明降水可能性的大小,概率值越大只能表示在一次试验中发生的可能性越大。在一次试验中“降水”这个事件是否发生仍然是随机的。孟德尔小传 从维也纳大学回到布鲁恩不久,孟德尔就开始了长达8年的豌豆实验。孟德尔首先从许多种子商那里,弄来了34个品种的豌豆,从中挑选出22个品种用于实验。它们都具有某种可以相互区分的稳定性状,例如高茎或矮茎、圆料或皱科、灰色种皮或白色种皮等。 5、试验与发现.豌豆杂交试验孟德尔把黄色和绿色的豌豆杂交,第一年收获的豌豆是黄色的。第二年,当他把第一年收获的黄色豌豆再种下时,收获的豌豆既有黄色的又有绿色的。
同样他把圆形和皱皮豌豆杂交,第一年收获的都是圆形豌豆,连一粒皱皮豌豆都没有。第二年,当他把这种杂交圆形再种下时,得到的却既有圆形豌豆,又有皱皮豌豆。6、遗传机理中的统计规律第一代第二代概率先后抛掷两枚均匀的硬币。
(1)一共可以出现多少种不同的结果?
(2)出现“一枚正面,一枚反面”的结果有多少种?
(3)出现“一枚正面,一枚反面”的概率是多少?
(4)有人说:“一共可能出现‘2枚正面’、‘2枚反
面’、‘1枚正面,1枚反面’这三种结果,因此出现
‘1枚正面,1枚反面‘的概率是1/3”,这种说法对
不对?练习:小结作业1.概率的正确理解:
随机事件在一次实验中发生与否是随机的,但随
机性中含有规律性:即随着实验次数的增加,该随机事件发生的频率会越来越接近于该事件发生的概率。2.概率在实际问题中的应用:
(1)概率与公平性的关系:利用概率解释游戏规则的公平性,判断实际生活中的一些现象是否合理。
(2)概率与决策的关系:在“风险与决策”中经常会用到统计中的极大似然法:在一次实验中,概率大的事件发生的可能性大。
(3)概率与预报的关系:在对各种自然现象、灾害的研究过程中经常会用到概率的思想来进行预测。
(4)遗传机理中的统计规律.作业:P118 练习:1,2,3.
其中一等奖1个;二号箱子里有奖券100张,
其中有一等奖10个。而每个箱子的一等奖的
奖品是一样的,那么,请同学们告诉我要取
得一等奖,你们会建议我到哪个箱子摸奖?如果二号箱子里有奖券1000张,一等奖还是
有10个,你们会建议我到哪个箱子去摸奖?考察下列事件能否发生?
(1)导体通电时发热;
(2)向上抛出的石头会下落;
(3)在标准大气压下水温升高到100°C会 沸腾.
必然发生必然发生必然发生必然事件:在一定条件下必然要发生的事件叫必然事件;知识探究:必然事件、不可能事件、随机事件
不可能发生不可能发生不可能发生不可能事件:在一定条件下不可能发生的事件叫不可能事件;考察下列事件能否发生?
(1)在没有水分的真空中种子发芽;
(2)在常温常压下钢铁融化;
(3).知识探究:必然事件、不可能事件、随机事件
可能发生也可能不发生可能发生也可能不发生可能发生也可能不发生考察下列事件能否发生?
(1)某人射击一次命中目标;
(2)马林能夺取北京奥运会男
子乒乓球单打冠军;
(3)抛掷一个骰字出现的点数为偶数. 随机事件:在一定条件下可能发生也可能不发生的事件叫随机事件。知识探究:必然事件、不可能事件、随机事件指出下列事件是必然事件,不可能事件,还是随机事件:随机事件必然事件不可能事件随机事件随机事件练习指出下列事件中,哪些是不可能事件?哪些是必然事件?哪些是随机事件?
(1)若a、b、c都是实数,则a(bc)=(ab)c;
(2)没有空气,动物也能生存下去;
(3)在标准大气压下,水在温度90?C时沸腾;
(4)直线y=k(x+1)过定点(?1,0);
(5)某一天内电话收到的呼叫次数为0;
(6)一个袋内装有形状大小相同的一个白球和一个黑球,从中任意摸出1个球则为白球 必然事件不可能事件不可能事件必然事件随机事件随机事件思考解惑: 由于随机事件具有不确定性,因而从表
面看似乎偶然性在起支配作用,没有什么必
然性。但人们经过长期的实践并深入研究后,
发现随机事件虽然就每次试验结果来说,具
有不确定性,然而在大量重复实验中,它却
呈现出一种完全确定的规律性。下面请同学们来做抛掷硬币的实验: 实验一:频 数频 率 当抛掷硬币的次数很多时,出现正面的频率值是稳定的,接近于常数 0.5 ,在它附近摆动实验二:电脑抛掷硬币的实验 某批乒乓球产品质量检查结果表:当抽查的球数很多时,抽到优等品的频率 接近于常数0.95,在它附近摆动。思考1:从上面两个实验中你能得出什么结论?思考2:从这个实验中你又能得出什么结论?思考3:上述试验表明,随机事件在每次试验中是否发生是不能预知的,但是在大量重复试验后,随着试验次数的增加,事件A发生的频率呈现出一定的规律性,这个规律性是如何体现出来的? 事件发生的频率较稳定,在某个常数附近摆动. 思考4: 那么在上述抛掷硬币的试验中,正面向 上发生的概率是多少?思考5:在实际问题中,随机事件发生的概率往 往是未知的(如在一定条件下射击命中目标的概 率),你如何得到事件发生的概率? 通过大量重复试验得到事件A发生的频率的稳定值,即概率. 思考6:在相同条件下,事件A在先后两次试验中发生的频率是否一定相等?事件A在先后两次试验中发生的概率 P(A)是否一定相等? 频率具有随机性,做同样次数的重复试验,事件A发生的频率可能不相同;概率是一个确定的数,是客观存在的,与每次试验无关.思考7:必然事件、不可能事件发生的概率分别为多少?概率的取值范围是什么? 概率的性质:(1)求一个事件的概率的基本方法是通过大量的重复试验;
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A的概率;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5)必然事件的概率为1,不可能事件的概率为0.因此0?P(A)?1 1.抛掷100枚质地均匀的硬币,有下列一些说法:
①全部出现正面向上是不可能事件;
②至少有1枚出现正面向上是必然事件;
③出现50枚正面向上50枚正面向下是随机事件,
以上说法中正确说法的个数为 ( )
A.0个 B.1个 C.2个 D.3个 2.下列说法正确的是 ( )
A.任何事件的概率总是在(0,1)之间
B.频率是客观存在的,与试验次数无关
C.随着试验次数的增加,频率一般会越来越接近概率
D.概率是随机的,在试验前不能确定
练一练BC
1、本节需掌握的知识:
①了解必然事件,不可能事件,随机事件的概念;
②理解随机事件的发生在大量重复试验下,呈现规律性;
③理解概率的意义及其性质。
2、必然事件、不可能事件、随机事件是在一定的条件下发生的,当条件变化时,事件的性质也发生变化。
3、必然事件与不可能事件可看作随机事件的两种特殊情况.因此,任何事件发生的概率都满足:0≤P(A)≤1。
4、随机事件在相同的条件下进行大量的试验时,呈现规律性,且频率 总是接近于常数P(A),称P(A)为事件的概率。3.1.2 概率的意义1、概率的正确理解问题1:有人说,既然抛掷一枚硬币出现正面 的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上。 你认为这种想法正确吗?让事实说话! 让我们做一个抛掷硬币的试验,观察它落地时的情况。每人各取一枚同样的硬币,连续两次抛掷,观察它落地后的朝向,并记录下结果,填入下表。重复上面的过程10次,把全班同学试验结果汇总,计算三种结果发生的频率。问题2:有人说,中奖率为 的彩
票,买1000张一定中奖,这种理解对吗? 说明:虽然中奖张数是随机的,但这种随机性中具有规律性。随着试验次数的增加,即随着买的彩票张数的增加,大约有
的彩票中奖。实际上,买1000张彩票中奖的
概率为 。
没有一张中奖也是有可能的,其概率近似为0.3677。2.概率与公平性的关系问题3:你有没有注意到在乒乓球、排球等体育比赛中,如何确定由哪一方先发球?你觉得那些方法对比赛双方公平吗?3.概率与决策的关系问题4:在一次试验中,连续10次投掷一枚骰子,结果出现的都是1点,你认为这个骰子的质地均匀吗?为什么? 如果我们面临的是从多个可选答案中挑选正确答案的决策任务,那么“使得样本出现的可能性最大”可以作为决策的准则,这种判断问题的方法称为极大似然法。极大似然法是统计中重要的统计思想方法之一。如果我们的判断结论能够使得样本出现的可能性最大,那么判断正确的可能性也最大,这种判断问题的方法称为似然法。似然法是统计中重要的统计思想方法之一。通过刚学过的概率知识我们可以推断,如果它是均匀的,通过试验和观察,可以发现出现各个面的可能性都应该是 ,从而连续10次出现1点的概率为
,这在一次试验(即连续10次抛掷一枚骰子)中是几乎不可能发生的(在一次试验中几乎不可能发生的事件称为小概率事件)。4、天气预报的概率解释 某地气象局预报说,明天本地降水概率为70%。你认为下面两个解释哪一个能代表气象局的观点?
(1)明天本地有70%的区域下雨,30%的区域不下雨;
(2)明天本地下雨的机会是70%。 (1)显然是不正确的,因为70%的概率是说降水的概率,而不是说70%的区域降水。正确的选择是(2)。 降水概率的大小只能说明降水可能性的大小,概率值越大只能表示在一次试验中发生的可能性越大。在一次试验中“降水”这个事件是否发生仍然是随机的。孟德尔小传 从维也纳大学回到布鲁恩不久,孟德尔就开始了长达8年的豌豆实验。孟德尔首先从许多种子商那里,弄来了34个品种的豌豆,从中挑选出22个品种用于实验。它们都具有某种可以相互区分的稳定性状,例如高茎或矮茎、圆料或皱科、灰色种皮或白色种皮等。 5、试验与发现.豌豆杂交试验孟德尔把黄色和绿色的豌豆杂交,第一年收获的豌豆是黄色的。第二年,当他把第一年收获的黄色豌豆再种下时,收获的豌豆既有黄色的又有绿色的。
同样他把圆形和皱皮豌豆杂交,第一年收获的都是圆形豌豆,连一粒皱皮豌豆都没有。第二年,当他把这种杂交圆形再种下时,得到的却既有圆形豌豆,又有皱皮豌豆。6、遗传机理中的统计规律第一代第二代概率先后抛掷两枚均匀的硬币。
(1)一共可以出现多少种不同的结果?
(2)出现“一枚正面,一枚反面”的结果有多少种?
(3)出现“一枚正面,一枚反面”的概率是多少?
(4)有人说:“一共可能出现‘2枚正面’、‘2枚反
面’、‘1枚正面,1枚反面’这三种结果,因此出现
‘1枚正面,1枚反面‘的概率是1/3”,这种说法对
不对?练习:小结作业1.概率的正确理解:
随机事件在一次实验中发生与否是随机的,但随
机性中含有规律性:即随着实验次数的增加,该随机事件发生的频率会越来越接近于该事件发生的概率。2.概率在实际问题中的应用:
(1)概率与公平性的关系:利用概率解释游戏规则的公平性,判断实际生活中的一些现象是否合理。
(2)概率与决策的关系:在“风险与决策”中经常会用到统计中的极大似然法:在一次实验中,概率大的事件发生的可能性大。
(3)概率与预报的关系:在对各种自然现象、灾害的研究过程中经常会用到概率的思想来进行预测。
(4)遗传机理中的统计规律.作业:P118 练习:1,2,3.
