山东省巨野县第一中学人教A版高中数学必修四《1.1.1 任意角》课件(共24张PPT)
文档属性
| 名称 | 山东省巨野县第一中学人教A版高中数学必修四《1.1.1 任意角》课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-19 19:52:53 | ||
图片预览







文档简介
课件24张PPT。必修四 第一章三角函数
1.1.1任意角目标重点难点1)理解任意角的概念;
2)学会建立适当的坐标系来讨论角并理解“正角”“负角”“象限角”“终边相同的角”的含义。 理解“正角”、“负角”、“象限角”、“终边相同的角”的含义 “终边相同的角”的含义回忆:在初中角是如何定义的?
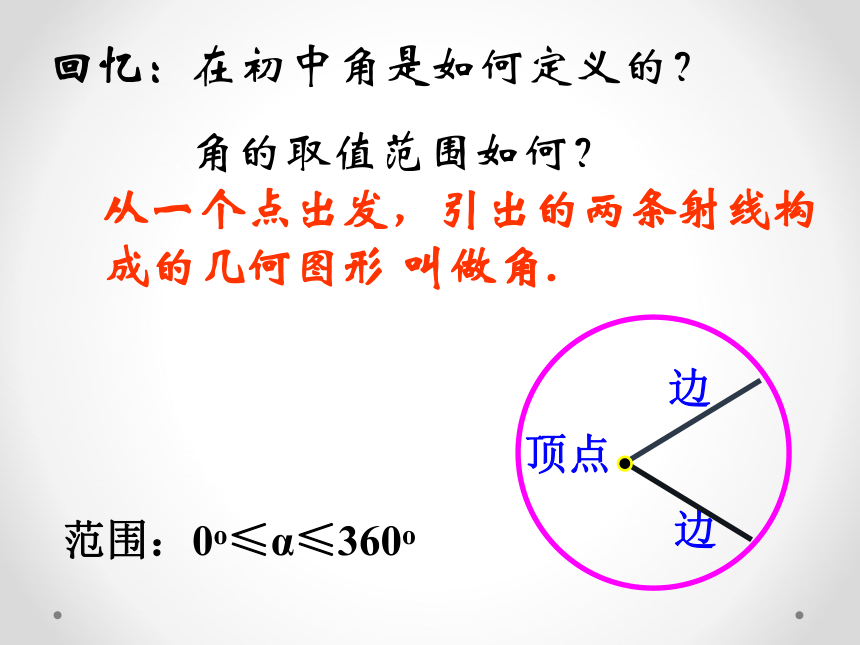
角的取值范围如何?从一个点出发,引出的两条射线构成的几何图形 叫做角.顶点边边范围:0o≤α≤360o程菲跳:
踺子后手翻转体180度接前直空翻540度307C:
反身翻腾
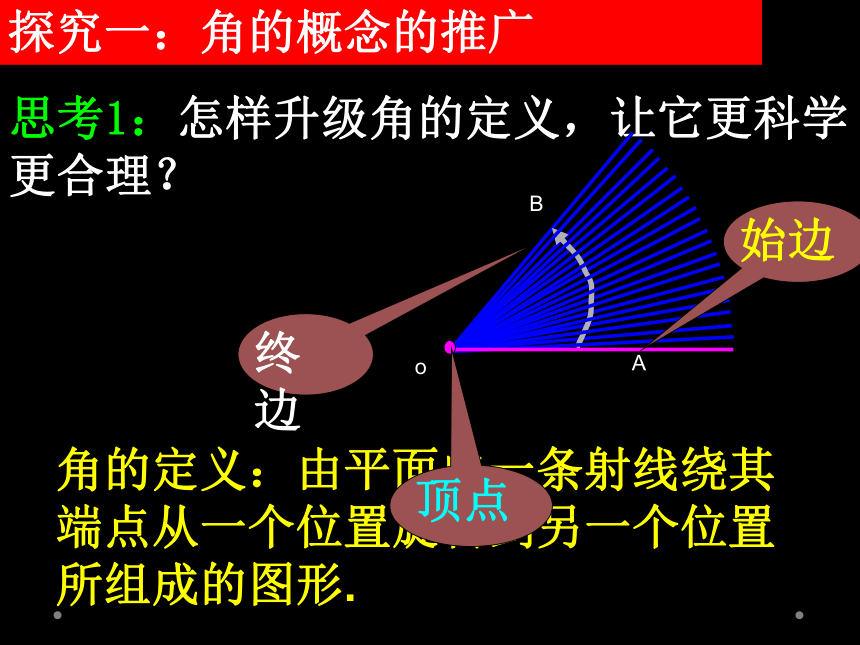
3周半(抱膝)探究一:角的概念的推广 思考1:怎样升级角的定义,让它更科学更合理?角的定义:由平面内一条射线绕其端点从一个位置旋转到另一个位置所组成的图形.oAB思考2:为了区分形成角的两种不同的旋转方向,可以作怎样的规定?如果一条射线没有作任何旋转,它还形成一个角吗? 规定:
按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角.
如果一条射线没有作任何旋转,则称它形成了一个零角. α=0°2、角的分类:正角:按逆时针方向旋转形成的角负角:按顺时针方向旋转形成的角 零角:射线不作旋转时形成的角任意角记法:角 或 ,可简记为 画图表示一个大小一定的角,先画一条射线作为角的始边,再由角的正负确定角的旋转方向,再由角的绝对值大小确定角的旋转量,画出角的终边,并用带箭头的螺旋线加以标注. 思考3:度量一个角的大小,既要考虑旋转方向,又要考虑旋转量,对于α=210°, =-150°,=-660°,你能用图形表示这些角吗?你能总结一下作图的要点吗? 探究二:象限角 思考4:为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么对一个任意角,角的终边可能落在哪些位置?
如何定义这些角? 1)角的顶点于坐标原点重合2)始边与X的非负半轴重合终边落在第几象限就称角是第几象限角终边落在坐标轴上就称角是轴线角
练习1:下列各角:-50°,405°,210°,-200°,
-450°分别是第几象限的角?-450°思考5:锐角与第一象限的角是什么逻辑关系?钝角与第二象限的角是什么逻辑关系?直角与轴线角是什么逻辑关系?思考6:第二象限的角一定比第一象限的角大吗? 象限角只能反映角的终边所在象限,不能反映角的大小. 练习2:请在坐标轴上画出30°,390°,
-330°,并找出它们的共同点?390?=30?+360??330?=30??360?思考7:与30°角终边相同的角有多少个? 这些角与30°角在数量上相差多少? 思考8:所有与30°角终边相同的角,连同30°角在内,可构成一个集合S,你能用描述法表示集合S吗? S={β|β=30°+k·360°,k∈Z}k·360°(k∈Z)结论:
所有与?终边相同的角连同?在内可以构成一个集合: 即:任何一个与角?终边相同的角,都可以表示成角?与整数个周角的和{β| β=α+k·360o}(k∈Z)例1. 在0o到360o范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角.
(1) -120o;(2) 640o;(3) -950o12′.解:⑴∵-120o=-360o+240o,
∴240o的角与-120o的角终边相同,
它是第三象限角.
⑵ ∵640o=360o+280o,
∴280o的角与640o的角终边相同,
它是第四象限角.⑶ ∵-950o12’=-3×360o+129o48’,
∴129o48’的角与-950o12’的角终边相同,
它是第二象限角.例2. 写出与下列各角终边相同的角的集合S,并把S中在-360o~720o间的角写出来:
(1) 60o;(2) -21o;(3) 363o14′.解:(1) S={β| β=k·360o+60o (k∈Z) },
S中在-360o~720o间的角是
-1×360o+60o=-280o;
0×360o+60o=60o;
1×360o+60o=420o.(2) S={β| β=k·360o-21o (k∈Z) }
S中在-360o~720o间的角是
0×360o-21o=-21o;
1×360o-21o=339o;
2×360o-21o=699o.(3) {β| β=k·360o+ 363o14’ (k∈Z) }
S中在-360o~720o间的角是
-2×360o+363o14’=-356o46’;
-1×360o+363o14’=3o14’;
0×360o+363o14’=363o14’.例3. 写出终边在y轴上的角的集合.解:与90°终边相同的角构成集合
S1={β|β=90°+k·360°,k∈Z}
与270°角终边相同的角构成集合
S2={β|β=270°+k·360°,k∈Z}
终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+k·360°,k∈Z} ∪{β|β=270°+k·360°,k∈Z}
={β|β=90°+2k·180°,k∈Z} ∪{β|β=90°+(2k+1)·180°,k∈Z}
={β|β=90°+n·180°,n∈Z}变式:α的终边在下图所示的阴影范围内,
写出α组成的集合.当堂反馈1.经过2个小时,钟表上的时针旋转了( )
A.60° B.-60°
C.30° D.-30°
2.下列命题中的真命题是( )
A.三角形的内角必是第一象限或
第二象限的角
B.钝角都是第二象限角
C.终边相同的角必相等
D.终边在第二象限的角是钝角BB3. 与-2012°终边相同的最大负角是_____.
4.终边落在射线 上的角的集合为_____________________________.
5. 如图所示.
(1)分别写出终边落在
OA,OB位置上的角
的集合;
(2)写出终边落在阴影
部分(包括边界)的角
的集合.
-212°S={β| β=60o +k·360o (k∈Z) },小结:本节课你学到了什么?课后作业:
1、巩固所学:
必修四教材 习题1.1 A组1、3
2、预习探求:思考下列问题
(1)第一、二、三、四象限的角的集合分别如何表示?
(2) 如果α是第二象限的角,那么2α、α/2分别是第几象限的角?
1.1.1任意角目标重点难点1)理解任意角的概念;
2)学会建立适当的坐标系来讨论角并理解“正角”“负角”“象限角”“终边相同的角”的含义。 理解“正角”、“负角”、“象限角”、“终边相同的角”的含义 “终边相同的角”的含义回忆:在初中角是如何定义的?
角的取值范围如何?从一个点出发,引出的两条射线构成的几何图形 叫做角.顶点边边范围:0o≤α≤360o程菲跳:
踺子后手翻转体180度接前直空翻540度307C:
反身翻腾
3周半(抱膝)探究一:角的概念的推广 思考1:怎样升级角的定义,让它更科学更合理?角的定义:由平面内一条射线绕其端点从一个位置旋转到另一个位置所组成的图形.oAB思考2:为了区分形成角的两种不同的旋转方向,可以作怎样的规定?如果一条射线没有作任何旋转,它还形成一个角吗? 规定:
按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角.
如果一条射线没有作任何旋转,则称它形成了一个零角. α=0°2、角的分类:正角:按逆时针方向旋转形成的角负角:按顺时针方向旋转形成的角 零角:射线不作旋转时形成的角任意角记法:角 或 ,可简记为 画图表示一个大小一定的角,先画一条射线作为角的始边,再由角的正负确定角的旋转方向,再由角的绝对值大小确定角的旋转量,画出角的终边,并用带箭头的螺旋线加以标注. 思考3:度量一个角的大小,既要考虑旋转方向,又要考虑旋转量,对于α=210°, =-150°,=-660°,你能用图形表示这些角吗?你能总结一下作图的要点吗? 探究二:象限角 思考4:为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么对一个任意角,角的终边可能落在哪些位置?
如何定义这些角? 1)角的顶点于坐标原点重合2)始边与X的非负半轴重合终边落在第几象限就称角是第几象限角终边落在坐标轴上就称角是轴线角
练习1:下列各角:-50°,405°,210°,-200°,
-450°分别是第几象限的角?-450°思考5:锐角与第一象限的角是什么逻辑关系?钝角与第二象限的角是什么逻辑关系?直角与轴线角是什么逻辑关系?思考6:第二象限的角一定比第一象限的角大吗? 象限角只能反映角的终边所在象限,不能反映角的大小. 练习2:请在坐标轴上画出30°,390°,
-330°,并找出它们的共同点?390?=30?+360??330?=30??360?思考7:与30°角终边相同的角有多少个? 这些角与30°角在数量上相差多少? 思考8:所有与30°角终边相同的角,连同30°角在内,可构成一个集合S,你能用描述法表示集合S吗? S={β|β=30°+k·360°,k∈Z}k·360°(k∈Z)结论:
所有与?终边相同的角连同?在内可以构成一个集合: 即:任何一个与角?终边相同的角,都可以表示成角?与整数个周角的和{β| β=α+k·360o}(k∈Z)例1. 在0o到360o范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角.
(1) -120o;(2) 640o;(3) -950o12′.解:⑴∵-120o=-360o+240o,
∴240o的角与-120o的角终边相同,
它是第三象限角.
⑵ ∵640o=360o+280o,
∴280o的角与640o的角终边相同,
它是第四象限角.⑶ ∵-950o12’=-3×360o+129o48’,
∴129o48’的角与-950o12’的角终边相同,
它是第二象限角.例2. 写出与下列各角终边相同的角的集合S,并把S中在-360o~720o间的角写出来:
(1) 60o;(2) -21o;(3) 363o14′.解:(1) S={β| β=k·360o+60o (k∈Z) },
S中在-360o~720o间的角是
-1×360o+60o=-280o;
0×360o+60o=60o;
1×360o+60o=420o.(2) S={β| β=k·360o-21o (k∈Z) }
S中在-360o~720o间的角是
0×360o-21o=-21o;
1×360o-21o=339o;
2×360o-21o=699o.(3) {β| β=k·360o+ 363o14’ (k∈Z) }
S中在-360o~720o间的角是
-2×360o+363o14’=-356o46’;
-1×360o+363o14’=3o14’;
0×360o+363o14’=363o14’.例3. 写出终边在y轴上的角的集合.解:与90°终边相同的角构成集合
S1={β|β=90°+k·360°,k∈Z}
与270°角终边相同的角构成集合
S2={β|β=270°+k·360°,k∈Z}
终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+k·360°,k∈Z} ∪{β|β=270°+k·360°,k∈Z}
={β|β=90°+2k·180°,k∈Z} ∪{β|β=90°+(2k+1)·180°,k∈Z}
={β|β=90°+n·180°,n∈Z}变式:α的终边在下图所示的阴影范围内,
写出α组成的集合.当堂反馈1.经过2个小时,钟表上的时针旋转了( )
A.60° B.-60°
C.30° D.-30°
2.下列命题中的真命题是( )
A.三角形的内角必是第一象限或
第二象限的角
B.钝角都是第二象限角
C.终边相同的角必相等
D.终边在第二象限的角是钝角BB3. 与-2012°终边相同的最大负角是_____.
4.终边落在射线 上的角的集合为_____________________________.
5. 如图所示.
(1)分别写出终边落在
OA,OB位置上的角
的集合;
(2)写出终边落在阴影
部分(包括边界)的角
的集合.
-212°S={β| β=60o +k·360o (k∈Z) },小结:本节课你学到了什么?课后作业:
1、巩固所学:
必修四教材 习题1.1 A组1、3
2、预习探求:思考下列问题
(1)第一、二、三、四象限的角的集合分别如何表示?
(2) 如果α是第二象限的角,那么2α、α/2分别是第几象限的角?
