山东省巨野县第一中学人教A版高中数学必修四《1.4 正切函数图象与性质》课件(共24张PPT)
文档属性
| 名称 | 山东省巨野县第一中学人教A版高中数学必修四《1.4 正切函数图象与性质》课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 508.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-19 20:34:48 | ||
图片预览





文档简介
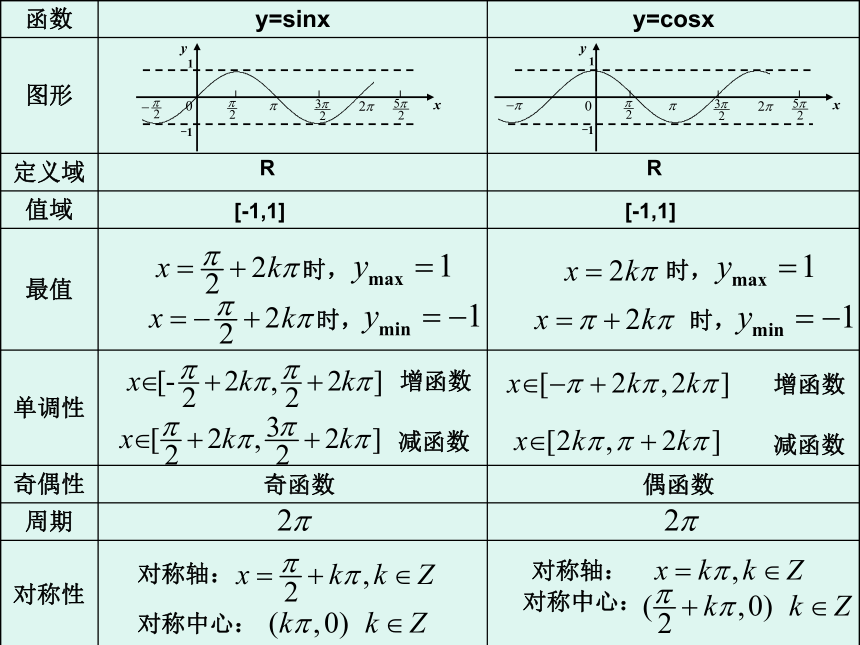
课件24张PPT。1.4.3正切函数的图象及性质时,时,时,时,增函数减函数增函数减函数对称轴:对称中心:对称轴:对称中心:奇函数偶函数RR[-1,1][-1,1] 一、你能否根据研究正弦、余弦函数的图象和性质的经验 以同样的方法研究正切函数
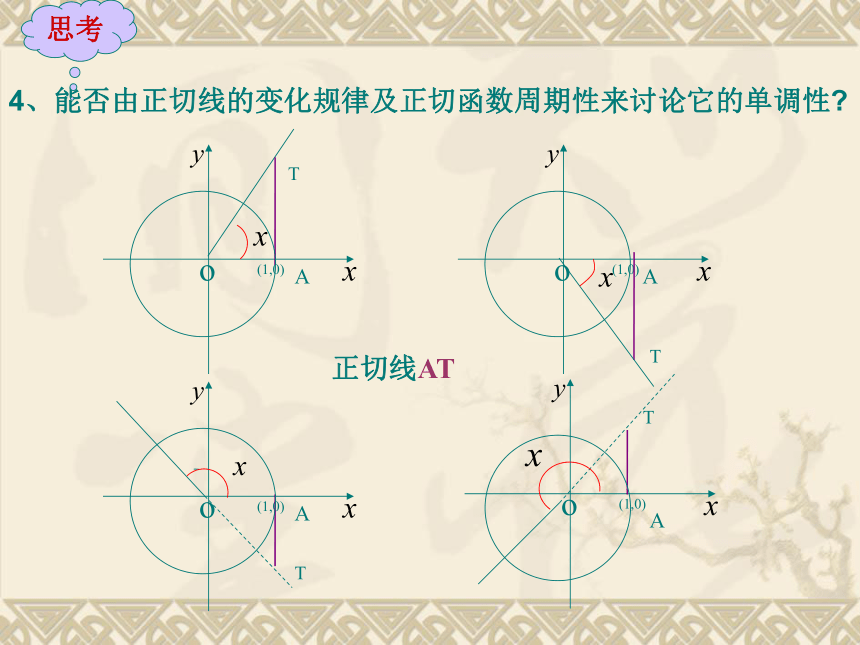
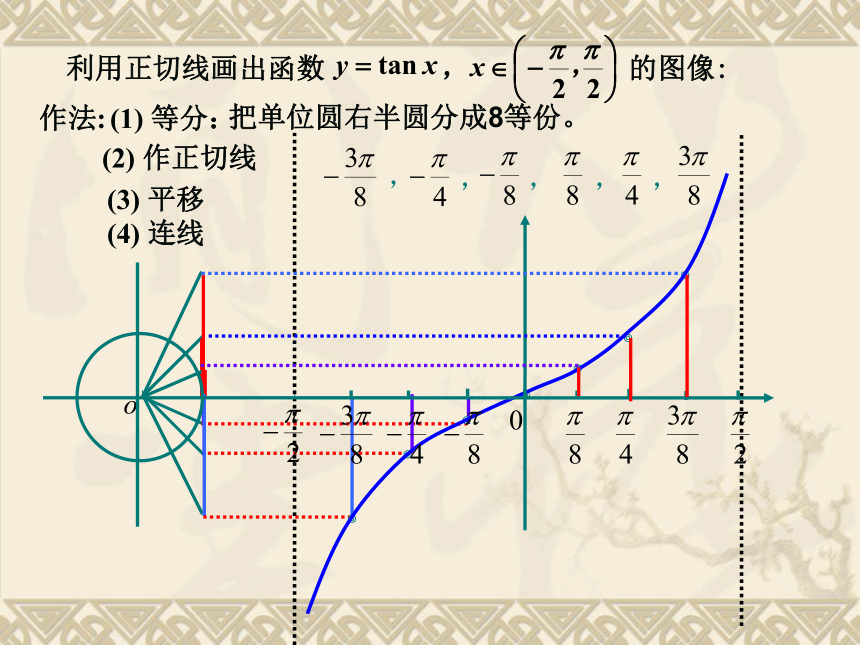
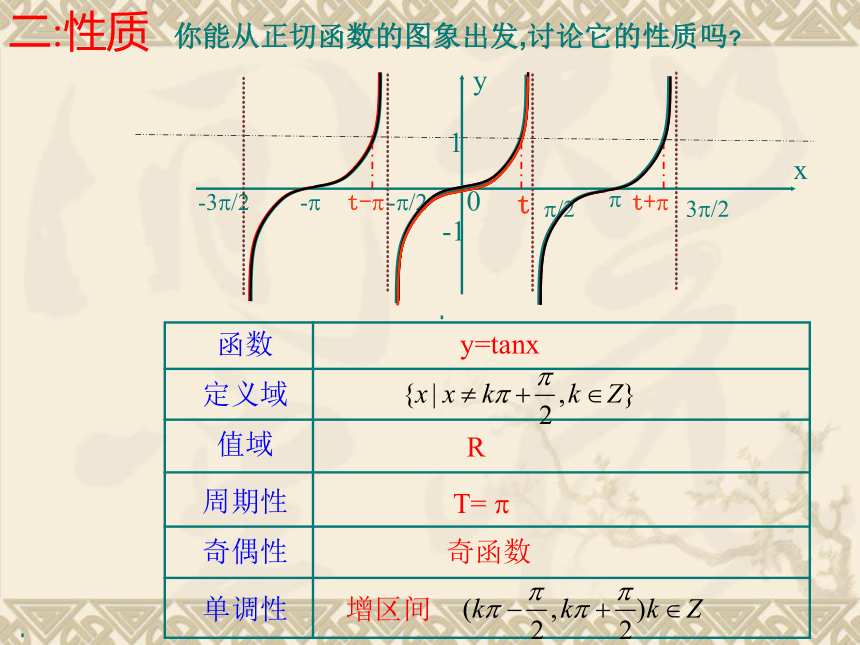
的图像和性质?探究1、利用正切函数的定义,说出正切函数的定义域; ∴ 是周期函数, 是它的一个周期. 思考由诱导公式知2、正切函数 是否为周期函数? 3、正切函数 是否具有奇偶性? 思考由诱导公式知正切函数是奇函数. 4、能否由正切线的变化规律及正切函数周期性来讨论它的单调性?思考AT正切线ATATATAT作法:(1) 等分:(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成8等份。利用正切线画出函数 , 的图像: 正切函数图象的简单画法:三点两线法。“三点”:“两线”:1-1yx1-1?/2-?/2?3?/2-3?/2-?0定义域值域周期性奇偶性单调性 RT= ?奇函数 函数y=tanx增区间二:性质tt+?t-?你能从正切函数的图象出发,讨论它的性质吗?正切曲线0是由通过点 且与 y 轴相互平行的
直线隔开的无穷多支曲线组成 正切函数的图像和性质⑴ 定义域:⑵ 值域:⑶ 周期性:⑷ 奇偶性: 在每一个开区间
, 内都是增函数。正
切
函
数
图
像奇函数,图象关于原点对称。R⑸ 单调性:(6)渐近线方程: (7)对称中心渐进线性质 :渐进线(1)正切函数是整个定义域上的增函数吗?为什么?(2)正切函数会不会在某一区间内是减函数?为什么? 问题: 在每一个开区间
, 内都是增函数。问 题 讨 论A 是奇函数
B 在整个定义域上是增函数
C 在定义域内无最大值和最小值
D 平行于 轴的的直线被正切曲线各支所截线段相等
1.关于正切函数 , 下列判断不正确的是( )2.函数 的一个对称中心是( )A . B. C. D. 基础练习BC例1、比较下列每组数的大小。说明:比较两个正切值大小,关键是把相应的角 化到y=tanx的同一单调区间内,再利用y=tanx的单调递增性解决。例题分析解:(1) 又∵ ,函数 ,
是增函数, ∴ 即 . 例1、比较下列每组数的大小。解:<>2、求函数y=tan3x的定义域,值域,单调增区间。反馈演练解:例 2例题分析反馈演练答案: 1.2.2、求函数 的周期.这说明自变量 x ,至少要增加 ,函数的值才能重复取得,所以函数 的周期
是 例3反馈练习:求下列函数的周期:例题分析解: 例4 求下列函数的单调区间:这个题目应该注意什么求函数 的定义域、值域,并指出它的
单调性、奇偶性和周期性;提高练习答案:四、小结:正切函数的图像和性质 2 、 性质:⑴ 定义域:⑷ 奇偶性: 在每一个开区间
, 内都是增函数。奇函数,图象关于原点对称。R(6)单调性:(7)渐近线方程: (5) 对称性:对称中心: 无对称轴
的图像和性质?探究1、利用正切函数的定义,说出正切函数的定义域; ∴ 是周期函数, 是它的一个周期. 思考由诱导公式知2、正切函数 是否为周期函数? 3、正切函数 是否具有奇偶性? 思考由诱导公式知正切函数是奇函数. 4、能否由正切线的变化规律及正切函数周期性来讨论它的单调性?思考AT正切线ATATATAT作法:(1) 等分:(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成8等份。利用正切线画出函数 , 的图像: 正切函数图象的简单画法:三点两线法。“三点”:“两线”:1-1yx1-1?/2-?/2?3?/2-3?/2-?0定义域值域周期性奇偶性单调性 RT= ?奇函数 函数y=tanx增区间二:性质tt+?t-?你能从正切函数的图象出发,讨论它的性质吗?正切曲线0是由通过点 且与 y 轴相互平行的
直线隔开的无穷多支曲线组成 正切函数的图像和性质⑴ 定义域:⑵ 值域:⑶ 周期性:⑷ 奇偶性: 在每一个开区间
, 内都是增函数。正
切
函
数
图
像奇函数,图象关于原点对称。R⑸ 单调性:(6)渐近线方程: (7)对称中心渐进线性质 :渐进线(1)正切函数是整个定义域上的增函数吗?为什么?(2)正切函数会不会在某一区间内是减函数?为什么? 问题: 在每一个开区间
, 内都是增函数。问 题 讨 论A 是奇函数
B 在整个定义域上是增函数
C 在定义域内无最大值和最小值
D 平行于 轴的的直线被正切曲线各支所截线段相等
1.关于正切函数 , 下列判断不正确的是( )2.函数 的一个对称中心是( )A . B. C. D. 基础练习BC例1、比较下列每组数的大小。说明:比较两个正切值大小,关键是把相应的角 化到y=tanx的同一单调区间内,再利用y=tanx的单调递增性解决。例题分析解:(1) 又∵ ,函数 ,
是增函数, ∴ 即 . 例1、比较下列每组数的大小。解:<>2、求函数y=tan3x的定义域,值域,单调增区间。反馈演练解:例 2例题分析反馈演练答案: 1.2.2、求函数 的周期.这说明自变量 x ,至少要增加 ,函数的值才能重复取得,所以函数 的周期
是 例3反馈练习:求下列函数的周期:例题分析解: 例4 求下列函数的单调区间:这个题目应该注意什么求函数 的定义域、值域,并指出它的
单调性、奇偶性和周期性;提高练习答案:四、小结:正切函数的图像和性质 2 、 性质:⑴ 定义域:⑷ 奇偶性: 在每一个开区间
, 内都是增函数。奇函数,图象关于原点对称。R(6)单调性:(7)渐近线方程: (5) 对称性:对称中心: 无对称轴
