山东省巨野县第一中学人教A版高中数学必修一《第一章 集合与函数概念》复习课件(共55张PPT)
文档属性
| 名称 | 山东省巨野县第一中学人教A版高中数学必修一《第一章 集合与函数概念》复习课件(共55张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-19 21:01:00 | ||
图片预览











文档简介
课件55张PPT。 1.1 集合第一章 集合与函数概念集合的有关概念元素(element)---我们把研究的对象统称为元素
集合(set)---把一些元素组成的总体叫做集合, 简称集.
一般用大括号”{ }”表示集合,也常用大写的拉丁字母A、B、C…表示集合.
用小写的拉丁字母a,b,c…表示元素注:组成集合的元素可以是物,数,图,点等1.1.1 集合的含义与表示集合三大特性:(2)互异性:集合中的元素必须是互不相同的。(1)确定性:集合中的元素必须是确定的. (3)无序性:集合中的元素是无先后顺序的.
集合中的任何两个元素都可以交换位置.只要构成两个集合的元素是一样的,我们就称这两个集合是相等的 重要数集:(1) N: 自然数集(含0)(2) N+或N﹡ : 正整数集(不含0)(3) Z:整数集(4) Q:有理数集(5) R:实数集即非负整数集(1)属于(belong to):如果a是集合A的元素,就说a属于A,记作a∈A(2)不属于(not belong to):如果a不是集合A的元素,就说a不属于A,记作元素对于集合的关系练一练:∈∈∈∈集合的表示方法 1、列举法: 将集合中的元素一一列举出来,并用花括号{ }
括起来的方法叫做列举法互异无序集合的表示方法 2、描述法:将集合的所有元素都具有的性质(满足的条件)
表示出来,写成{x︱p(x)}的形式特征性质例:试分别用列举法和描述法表示下列集合:
(1)方程x2-2=0的所有实数根组成的集合;
(2)由大于10小于20的所有整数组成的集合。 例:已知A={a-2,2a2+5a,10},且-3∈A,求a。 1.1.2
集合间的基本关系 定 义
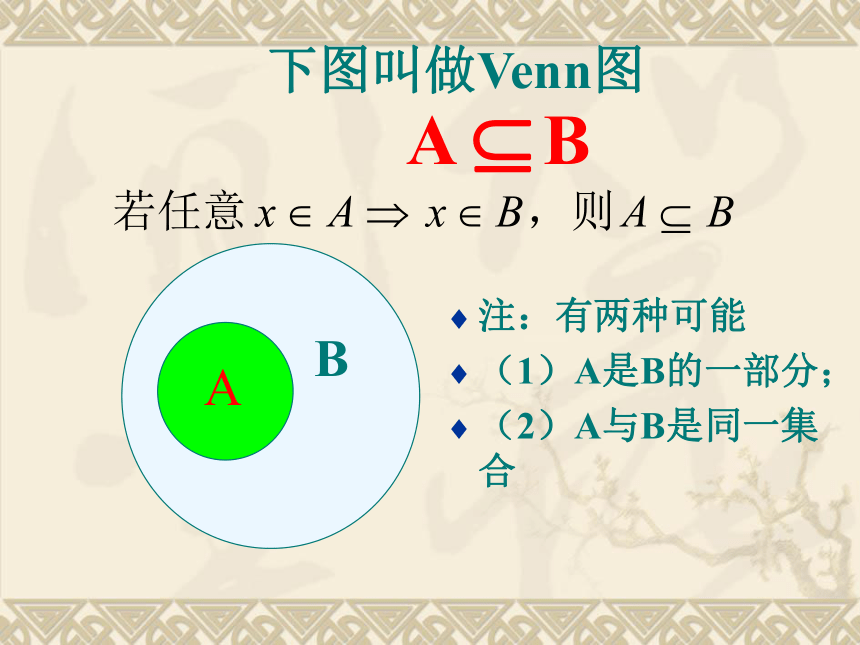
一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集(subset)BA BA下图叫做Venn图 注:有两种可能
(1)A是B的一部分;
(2)A与B是同一集合 一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,同时集合B中的任何一个元素都是集合A的元素,则称集合A等于集合B,记作 A=B定 义若A B且B A,则A=B;反之,亦然.定 义Venn图为AB 几个结论①空集是任何集合的子集Φ A
②空集是任何非空集合的真子集
Φ A (A ≠ Φ)
③任何一个集合是它本身的子集,即 A A
④对于集合A,B,C,如果 A B,
且B C,则A C
注意易混符号 ①“∈ ”与“ ”:元素与集合之间是属于关系;集合与集合之间是包含关系如
Φ R,{1} {1,2,3}
②{0}与Φ:{0}是含有一个元素0的集合,Φ是不含任何元素的集合.
Φ {0}不能写成Φ={0},Φ∈{0}重要结论含n个元素的集合的所有子集的个数是2n,所有真子集的个数是2n-1,非空真子集数为2n-2.1.1.3 集合的基本运算定 义一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,记作 A∪B即A∪B={x | x∈A,或x∈B} 读作 A并 BA∪B例1. A={4,5,6,8},B={3,5,7,8},求A∪B.例2.设A={x|-1应关系f,使对于集合A中的任意一个数x,在集合B中
都有唯一确定的数f(x)和它对应,那么就称
f: A→B为从集合A到集合B的一个函数(fun_ction),
记作y=f (x),x∈A。定义域(domain):x的取值范围A叫做函数的定义域;
与x值相对应的y值叫做函数值。
值域(range):函数值的集合叫做函数的值域。注意:
①区间是一种表示连续性的数集
②定义域、值域经常用区间表示
③实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点。函数的三要素判断同一函数: 对应法则f、定义域A、值域只有当这三要素完全相同时,两个函数才能
称为同一函数。当有解析式时只要定义域与
解析式一样即可 例、下列函数中哪个与函数是同一个函数?定义域结论实数集R 使分母不等于0的实数的集合使根号内的式子大于或等于0的实数的集合使各部分式子都有意义的实数的集合(即各集合的交集)使实际问题有意义的实数的集合 1.2.2 函数的表示法一、函数的表示方法⑴解析法:就是把两个变量的函数关系,用
一个等式表示,这个等式叫做函数的解析表
达式,简称解析式. 注意:注明定义域⑵列表法:就是列出表格来表示两个变量
的函数关系 ⑶图象法:就是用函数图象表示两个变量之
间的关系.函数图象既可以是连续的曲线,也可以是直线、
折线、离散的点等。求函数解析式的方法:待定系数法;配凑法;
换元法;解方程组法(注意定义域)例.分别求下列条件下的f(x)(1)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)
=2x+17,求f(x) 待定系数法(2)已知f(x-1)=2x+3,求f(x) 配凑法或换元法(3)已知3f(x)+2f(-x)=x+3,求f(x) 列方程组法二、分段函数例:作出的图像并求值域。(1)分段函数的表达式虽然不止一个,但它
不是几个函数,而是一个函数。
(2)分段函数的定义域是各段定义域的并集,
值域是各段值域的并集。三、映射:映射定义: 设A、B是两个非空的集合,如果
按某一个确定的对应法则f,使对于集合A中
的任意一个元素x,在集合B中都有唯一确定
的元素y与之对应,那么就称对应f:A为从集合A到集合B的一个映射(mapping).
记作“f:A举例分析映射实质:映射三要素:集合A、B以及对应法则,缺一不可;×1.3.1单调性与最大(小)值
1.3 函数的基本性质
(一)函数单调性定义思考:仿照增函数的定义说出减函数的定义. 注意:
① 函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
②必须是对于区间D内的任意两个自变量x1,x2;当x1 如果函数y=f(x)在某个区间上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间:注意:⑴函数的单调区间是其定义域的子集;⑵应是该区间内任意的两个实数,忽略需要任意取值这个条件,就不能保证函数是增函数(或减函数),例如,图5中,在那样的特定位置上,虽然使得f( )>f( ),但显然此图象表示的函数不是一个单调函数;(二)典型例题例.如图6是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,函数y=f(x)是增函数还是减函数. 3.判断函数单调性的方法步骤
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
① 任取x1,x2∈D,且x1② 作差f(x1)-f(x2);
③ 变形(通常是因式分解和配方);
④定号(即判断差f(x1)-f(x2)的正负);
⑤下结论(即指出函数f(x)在给定的区间D上的单调性). 4.最大值 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最大值 5.最小值 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≥M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最小值 2、函数最大(小)值应该是所有函数值中最大(小)的,即对于任意的x∈I,都有f(x)≤M(f(x)≥M). 注意:1、函数最大(小)值首先应该是某一个函数值,即存在x0∈I,使得f(x0) = M;练习1、函数f(x)=x2+4ax+2在区间(-∞,6]内递减,则a的取值范围是( )
A、a≥3 B、a≤3
C、a≥-3 D、a≤-3D2、已知函数f(x)=4x2-mx+1,在(-∞,-2]上递减,在[-2,+∞)上递增,则f(x)在[1,2]上的值域____________.[21,39]1.3.2函数的奇偶性1.偶函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数. f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1) 对于R内任意的一个x,都有f(-x)=-x=-f(x),这时我们称函数y=x为奇函数.f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)2.奇函数 注意: 1、函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;2、由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).3、奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则f(-x)=-f(x)有成立.
若f(x)为偶函数,则f(-x)=f(x)有成立.4、如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.3.用定义判断函数奇偶性的步骤:(1)、先求定义域,看是否关于原点对称;(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.4.奇偶函数图象的性质1、奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于原点对称,那么就称这个函数为奇函数.2、偶函数的图象关于y轴对称. 反过来,如果一个函数的图象关于y轴对称,那么就称这个函数为偶函数.
集合(set)---把一些元素组成的总体叫做集合, 简称集.
一般用大括号”{ }”表示集合,也常用大写的拉丁字母A、B、C…表示集合.
用小写的拉丁字母a,b,c…表示元素注:组成集合的元素可以是物,数,图,点等1.1.1 集合的含义与表示集合三大特性:(2)互异性:集合中的元素必须是互不相同的。(1)确定性:集合中的元素必须是确定的. (3)无序性:集合中的元素是无先后顺序的.
集合中的任何两个元素都可以交换位置.只要构成两个集合的元素是一样的,我们就称这两个集合是相等的 重要数集:(1) N: 自然数集(含0)(2) N+或N﹡ : 正整数集(不含0)(3) Z:整数集(4) Q:有理数集(5) R:实数集即非负整数集(1)属于(belong to):如果a是集合A的元素,就说a属于A,记作a∈A(2)不属于(not belong to):如果a不是集合A的元素,就说a不属于A,记作元素对于集合的关系练一练:∈∈∈∈集合的表示方法 1、列举法: 将集合中的元素一一列举出来,并用花括号{ }
括起来的方法叫做列举法互异无序集合的表示方法 2、描述法:将集合的所有元素都具有的性质(满足的条件)
表示出来,写成{x︱p(x)}的形式特征性质例:试分别用列举法和描述法表示下列集合:
(1)方程x2-2=0的所有实数根组成的集合;
(2)由大于10小于20的所有整数组成的集合。 例:已知A={a-2,2a2+5a,10},且-3∈A,求a。 1.1.2
集合间的基本关系 定 义
一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集(subset)BA BA下图叫做Venn图 注:有两种可能
(1)A是B的一部分;
(2)A与B是同一集合 一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,同时集合B中的任何一个元素都是集合A的元素,则称集合A等于集合B,记作 A=B定 义若A B且B A,则A=B;反之,亦然.定 义Venn图为AB 几个结论①空集是任何集合的子集Φ A
②空集是任何非空集合的真子集
Φ A (A ≠ Φ)
③任何一个集合是它本身的子集,即 A A
④对于集合A,B,C,如果 A B,
且B C,则A C
注意易混符号 ①“∈ ”与“ ”:元素与集合之间是属于关系;集合与集合之间是包含关系如
Φ R,{1} {1,2,3}
②{0}与Φ:{0}是含有一个元素0的集合,Φ是不含任何元素的集合.
Φ {0}不能写成Φ={0},Φ∈{0}重要结论含n个元素的集合的所有子集的个数是2n,所有真子集的个数是2n-1,非空真子集数为2n-2.1.1.3 集合的基本运算定 义一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,记作 A∪B即A∪B={x | x∈A,或x∈B} 读作 A并 BA∪B例1. A={4,5,6,8},B={3,5,7,8},求A∪B.例2.设A={x|-1
都有唯一确定的数f(x)和它对应,那么就称
f: A→B为从集合A到集合B的一个函数(fun_ction),
记作y=f (x),x∈A。定义域(domain):x的取值范围A叫做函数的定义域;
与x值相对应的y值叫做函数值。
值域(range):函数值的集合叫做函数的值域。注意:
①区间是一种表示连续性的数集
②定义域、值域经常用区间表示
③实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点。函数的三要素判断同一函数: 对应法则f、定义域A、值域只有当这三要素完全相同时,两个函数才能
称为同一函数。当有解析式时只要定义域与
解析式一样即可 例、下列函数中哪个与函数是同一个函数?定义域结论实数集R 使分母不等于0的实数的集合使根号内的式子大于或等于0的实数的集合使各部分式子都有意义的实数的集合(即各集合的交集)使实际问题有意义的实数的集合 1.2.2 函数的表示法一、函数的表示方法⑴解析法:就是把两个变量的函数关系,用
一个等式表示,这个等式叫做函数的解析表
达式,简称解析式. 注意:注明定义域⑵列表法:就是列出表格来表示两个变量
的函数关系 ⑶图象法:就是用函数图象表示两个变量之
间的关系.函数图象既可以是连续的曲线,也可以是直线、
折线、离散的点等。求函数解析式的方法:待定系数法;配凑法;
换元法;解方程组法(注意定义域)例.分别求下列条件下的f(x)(1)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)
=2x+17,求f(x) 待定系数法(2)已知f(x-1)=2x+3,求f(x) 配凑法或换元法(3)已知3f(x)+2f(-x)=x+3,求f(x) 列方程组法二、分段函数例:作出的图像并求值域。(1)分段函数的表达式虽然不止一个,但它
不是几个函数,而是一个函数。
(2)分段函数的定义域是各段定义域的并集,
值域是各段值域的并集。三、映射:映射定义: 设A、B是两个非空的集合,如果
按某一个确定的对应法则f,使对于集合A中
的任意一个元素x,在集合B中都有唯一确定
的元素y与之对应,那么就称对应f:A为从集合A到集合B的一个映射(mapping).
记作“f:A举例分析映射实质:映射三要素:集合A、B以及对应法则,缺一不可;×1.3.1单调性与最大(小)值
1.3 函数的基本性质
(一)函数单调性定义思考:仿照增函数的定义说出减函数的定义. 注意:
① 函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
②必须是对于区间D内的任意两个自变量x1,x2;当x1
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
① 任取x1,x2∈D,且x1
③ 变形(通常是因式分解和配方);
④定号(即判断差f(x1)-f(x2)的正负);
⑤下结论(即指出函数f(x)在给定的区间D上的单调性). 4.最大值 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最大值 5.最小值 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≥M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最小值 2、函数最大(小)值应该是所有函数值中最大(小)的,即对于任意的x∈I,都有f(x)≤M(f(x)≥M). 注意:1、函数最大(小)值首先应该是某一个函数值,即存在x0∈I,使得f(x0) = M;练习1、函数f(x)=x2+4ax+2在区间(-∞,6]内递减,则a的取值范围是( )
A、a≥3 B、a≤3
C、a≥-3 D、a≤-3D2、已知函数f(x)=4x2-mx+1,在(-∞,-2]上递减,在[-2,+∞)上递增,则f(x)在[1,2]上的值域____________.[21,39]1.3.2函数的奇偶性1.偶函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数. f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1) 对于R内任意的一个x,都有f(-x)=-x=-f(x),这时我们称函数y=x为奇函数.f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)2.奇函数 注意: 1、函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;2、由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).3、奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则f(-x)=-f(x)有成立.
若f(x)为偶函数,则f(-x)=f(x)有成立.4、如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.3.用定义判断函数奇偶性的步骤:(1)、先求定义域,看是否关于原点对称;(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.4.奇偶函数图象的性质1、奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于原点对称,那么就称这个函数为奇函数.2、偶函数的图象关于y轴对称. 反过来,如果一个函数的图象关于y轴对称,那么就称这个函数为偶函数.
