吉林油田第十二中学2024—2025学年度第一学期月考测试初二数学试卷(PDF版,含简略答案)
文档属性
| 名称 | 吉林油田第十二中学2024—2025学年度第一学期月考测试初二数学试卷(PDF版,含简略答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 10:06:22 | ||
图片预览

文档简介
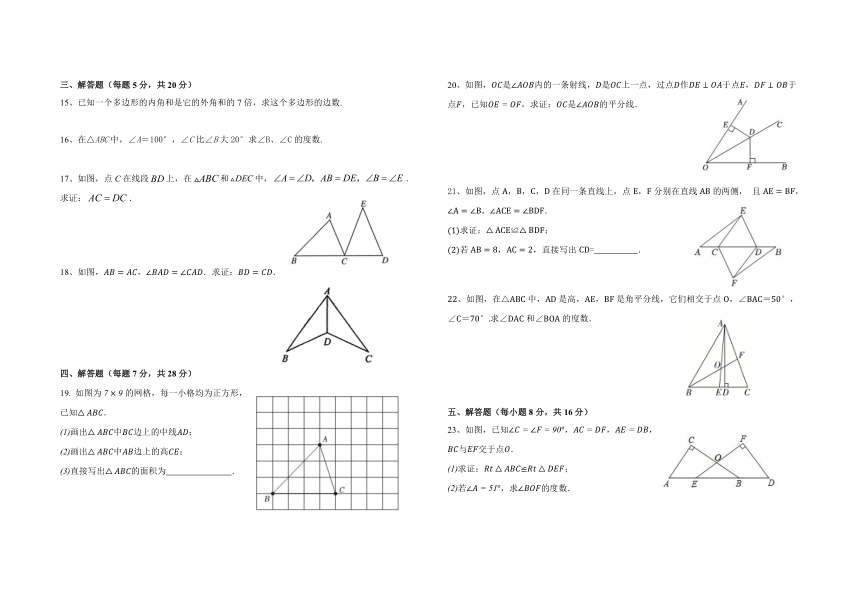
吉林油田第十二中学 2024—2025 年度第一学期 二、填空题(每题 3 分,共 24 分)
7、八边形内角和度数为 .
初二数学
8、如图,OP 平分 AOB,PC OB,如果 PC 6 ,那么点 P 到OA的距离等于 .
(考试时间:120 分钟)
一、选择题(每题 2 分,共 12 分)
1.以下长度的三根小木棒能摆成三角形的是 ( )
A.1,2,3 B.3,3,5 C.2,3,5 D.3,5,9
第 8题 第 9题 第 10题
2.下列各组图形中,属于全等图形的是( )
9、如图,钢架桥的设计中采用了三角形的结构,其数学道理是 .
10、如图,已知 AC BC 于点C ,CD AB于点 D, A 56 ,则 DCB的度数是 .
A. B. C. D.
11、已知等腰三角形的两条边长分别为 2 和 5,则它的周长是_____ _.
3.一个正多边形,它的每一个外角都等于 40°,则该正多边形是( )
12、如图,小红要测量池塘 A、B两端的距离,他设计了一个测量方案,先在平地上取可以直
A.正六边形 B.正七边形 C.正八边形 D.正九边形
接到达 A 点和 B 点的 C、D 两点,AC 与 BD 相交于点 O,且测得 AC BD 55m ,
4. 用直尺和圆规作一个角等于已知角,如图,能 OA OD 17m,△COD的周长为 103m,则 A、B两端的距离为_________m.
得出 AOB A O B 的依据是( )
A.SAS B.SSS
C.ASA D.AAS
5. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家
休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( ) 第 12题 第 13题 第 14题
A. △ 的三条中线的交点 B. △ 三边的中垂线的交点 13、如图,将正六边形与正方形按如图所示摆放,且正六边形的边 与正方形的边 在同一
C. △ 三条角平分线的交点 D. △ 三条高所在直线的交点 条直线上,则∠ 的度数是 .
6. 如图,两个三角形全等,则∠1的度数为( ) 14、如图,小明从点 A 出发沿直线前进 10 米到达点 B,向左转 45°后又沿直线前进 10 米到
A.50° B.58°
达点 C,再向左转 45°后沿直线前进 10 米到达点 D,……照这样走下去,小明第一次回到出
C.60° D.62°
发点 A时走过的路程为 .
三、解答题(每题 5 分,共 20 分) 20、如图, 是∠ 内的一条射线, 是 上一点,过点 作 ⊥ 于点 , ⊥ 于
15、已知一个多边形的内角和是它的外角和的 7倍,求这个多边形的边数. 点 ,已知 = ,求证: 是∠ 的平分线.
16、在△ABC 中,∠A=100°,∠C 比∠B 大 20°求∠B、∠C的度数.
17、如图,点 C在线段 BD上,在 ABC和 DEC中, A D,AB DE, B E .
21、如图,点 A,B,C,D在同一条直线上,点 E,F分别在直线 AB的两侧, 且 AE = BF,
求证: AC DC.
∠A = ∠B,∠ACE = ∠BDF.
(1)求证:△ ACE≌△ BDF;
(2)若 AB = 8,AC = 2,直接写出 CD= .
18、如图, = ,∠ = ∠ .求证: = .
22、如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点 O,∠BAC=50°,
∠C=70°.求∠DAC和∠BOA的度数.
四、解答题(每题 7 分,共 28 分)
19. 如图为 7 × 9的网格,每一小格均为正方形,
已知△ . 五、解答题(每小题 8 分,共 16 分)
(1)画出△ 中 边上的中线 ; 23、如图,已知∠ = ∠ = 90°, = , = ,
(2)画出△ 中 边上的高 ; 与 交于点 .
(3)直接写出△ 的面积为 . (1)求证: △ ≌ △ ;
(2)若∠ = 51°,求∠ 的度数.
24.【知识呈现】如图①,在△ABC 中,D是 BC的中点,过点 C作直线 CE,使CE∥ AB, 26、在△ 中, = ,∠ = 90°,直线 经过点 ,过 、 两点分别作 ⊥
交 AD的延长线于点 E,求证: AD ED;
于点 , ⊥ 于点 .
【应用】如图②,在四边形 ABCD中, AD∥ BC ,点 E是 CD的中点,射线 AE与 BC的延长
(1)如图 1,直接写出 、 、 三线段之间的等量关系;(不需写出证明过程)
线交于点 F,连接 BE,若 S△ABE 3,则 S四边形ABCD ______.
(2)若 绕点 旋转到(图 2)时,(1)中的关系还成立吗?若成立说明理由,若不成立请写出他
们之间的等量关系并说明理由.
(3)若 绕点 旋转到(图 3)时,请直接写出 、 、 三者之间的等量关系(不需写出证
明过程).
六、解答题(每小题 10 分,共 20 分)
25.(1)如图 1,在△ABC中,BD,CD分别是∠ABC,∠ACB的平分线,BD,CD相交于点
D. 探究∠D与∠A之间的数量关系.(需要写出证明过程)
(2)如图 2,BD,CD分别是△ABC的外角∠CBF,∠BCE的平分线,BD,CD相交于点 D.
直接写出∠D与∠A之间的数量关系.(不需写出证明过程)
(3)如图 3,在△ABC中,BD是∠ABC的平分线,CD是外角∠ACE的平分线,BD,CD相
交于点 D. 直接写出∠D与∠A之间的数量关系.(不需写出证明过程)
(4)如图 4,AC,BD相交于点 O,BP,CP分别是∠ABD,∠ACD的平分线,BP,CP相交
于点 P. 直接写出∠P与∠A,∠D之间的数量关系.(不需写出证明过程)
图 1 图 2 图 3 图 4
初二数学答案
一、1-6 BCCBCD
二、7、12 8、6 9、三角形具有稳定性 10、56°
11、 AB=DE 12、48 13、30° 14、80
三、15、十六边形
16、 ∠B=30° ∠C=50°
17、 略
18、 略
四、19、(1)(2)图略 (3)6
20、 证明略
21、 (1)证明略 (2)4
22、 ∠DAC=20° ∠BOA=125°
23、 (1)证明略 (2)∠BOF=78°
24、 (1)证明略 (2)6
25、 (1)∠D=90°+1/2∠A
(2)∠D=90°-1/2∠A
(3)∠D=1/2∠A
(4)∠P=1/2(∠A+∠D)
26、 (1)DE=BE+AD
(2)DE=BE-AD
(3)DE=AD-BE
7、八边形内角和度数为 .
初二数学
8、如图,OP 平分 AOB,PC OB,如果 PC 6 ,那么点 P 到OA的距离等于 .
(考试时间:120 分钟)
一、选择题(每题 2 分,共 12 分)
1.以下长度的三根小木棒能摆成三角形的是 ( )
A.1,2,3 B.3,3,5 C.2,3,5 D.3,5,9
第 8题 第 9题 第 10题
2.下列各组图形中,属于全等图形的是( )
9、如图,钢架桥的设计中采用了三角形的结构,其数学道理是 .
10、如图,已知 AC BC 于点C ,CD AB于点 D, A 56 ,则 DCB的度数是 .
A. B. C. D.
11、已知等腰三角形的两条边长分别为 2 和 5,则它的周长是_____ _.
3.一个正多边形,它的每一个外角都等于 40°,则该正多边形是( )
12、如图,小红要测量池塘 A、B两端的距离,他设计了一个测量方案,先在平地上取可以直
A.正六边形 B.正七边形 C.正八边形 D.正九边形
接到达 A 点和 B 点的 C、D 两点,AC 与 BD 相交于点 O,且测得 AC BD 55m ,
4. 用直尺和圆规作一个角等于已知角,如图,能 OA OD 17m,△COD的周长为 103m,则 A、B两端的距离为_________m.
得出 AOB A O B 的依据是( )
A.SAS B.SSS
C.ASA D.AAS
5. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家
休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( ) 第 12题 第 13题 第 14题
A. △ 的三条中线的交点 B. △ 三边的中垂线的交点 13、如图,将正六边形与正方形按如图所示摆放,且正六边形的边 与正方形的边 在同一
C. △ 三条角平分线的交点 D. △ 三条高所在直线的交点 条直线上,则∠ 的度数是 .
6. 如图,两个三角形全等,则∠1的度数为( ) 14、如图,小明从点 A 出发沿直线前进 10 米到达点 B,向左转 45°后又沿直线前进 10 米到
A.50° B.58°
达点 C,再向左转 45°后沿直线前进 10 米到达点 D,……照这样走下去,小明第一次回到出
C.60° D.62°
发点 A时走过的路程为 .
三、解答题(每题 5 分,共 20 分) 20、如图, 是∠ 内的一条射线, 是 上一点,过点 作 ⊥ 于点 , ⊥ 于
15、已知一个多边形的内角和是它的外角和的 7倍,求这个多边形的边数. 点 ,已知 = ,求证: 是∠ 的平分线.
16、在△ABC 中,∠A=100°,∠C 比∠B 大 20°求∠B、∠C的度数.
17、如图,点 C在线段 BD上,在 ABC和 DEC中, A D,AB DE, B E .
21、如图,点 A,B,C,D在同一条直线上,点 E,F分别在直线 AB的两侧, 且 AE = BF,
求证: AC DC.
∠A = ∠B,∠ACE = ∠BDF.
(1)求证:△ ACE≌△ BDF;
(2)若 AB = 8,AC = 2,直接写出 CD= .
18、如图, = ,∠ = ∠ .求证: = .
22、如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点 O,∠BAC=50°,
∠C=70°.求∠DAC和∠BOA的度数.
四、解答题(每题 7 分,共 28 分)
19. 如图为 7 × 9的网格,每一小格均为正方形,
已知△ . 五、解答题(每小题 8 分,共 16 分)
(1)画出△ 中 边上的中线 ; 23、如图,已知∠ = ∠ = 90°, = , = ,
(2)画出△ 中 边上的高 ; 与 交于点 .
(3)直接写出△ 的面积为 . (1)求证: △ ≌ △ ;
(2)若∠ = 51°,求∠ 的度数.
24.【知识呈现】如图①,在△ABC 中,D是 BC的中点,过点 C作直线 CE,使CE∥ AB, 26、在△ 中, = ,∠ = 90°,直线 经过点 ,过 、 两点分别作 ⊥
交 AD的延长线于点 E,求证: AD ED;
于点 , ⊥ 于点 .
【应用】如图②,在四边形 ABCD中, AD∥ BC ,点 E是 CD的中点,射线 AE与 BC的延长
(1)如图 1,直接写出 、 、 三线段之间的等量关系;(不需写出证明过程)
线交于点 F,连接 BE,若 S△ABE 3,则 S四边形ABCD ______.
(2)若 绕点 旋转到(图 2)时,(1)中的关系还成立吗?若成立说明理由,若不成立请写出他
们之间的等量关系并说明理由.
(3)若 绕点 旋转到(图 3)时,请直接写出 、 、 三者之间的等量关系(不需写出证
明过程).
六、解答题(每小题 10 分,共 20 分)
25.(1)如图 1,在△ABC中,BD,CD分别是∠ABC,∠ACB的平分线,BD,CD相交于点
D. 探究∠D与∠A之间的数量关系.(需要写出证明过程)
(2)如图 2,BD,CD分别是△ABC的外角∠CBF,∠BCE的平分线,BD,CD相交于点 D.
直接写出∠D与∠A之间的数量关系.(不需写出证明过程)
(3)如图 3,在△ABC中,BD是∠ABC的平分线,CD是外角∠ACE的平分线,BD,CD相
交于点 D. 直接写出∠D与∠A之间的数量关系.(不需写出证明过程)
(4)如图 4,AC,BD相交于点 O,BP,CP分别是∠ABD,∠ACD的平分线,BP,CP相交
于点 P. 直接写出∠P与∠A,∠D之间的数量关系.(不需写出证明过程)
图 1 图 2 图 3 图 4
初二数学答案
一、1-6 BCCBCD
二、7、12 8、6 9、三角形具有稳定性 10、56°
11、 AB=DE 12、48 13、30° 14、80
三、15、十六边形
16、 ∠B=30° ∠C=50°
17、 略
18、 略
四、19、(1)(2)图略 (3)6
20、 证明略
21、 (1)证明略 (2)4
22、 ∠DAC=20° ∠BOA=125°
23、 (1)证明略 (2)∠BOF=78°
24、 (1)证明略 (2)6
25、 (1)∠D=90°+1/2∠A
(2)∠D=90°-1/2∠A
(3)∠D=1/2∠A
(4)∠P=1/2(∠A+∠D)
26、 (1)DE=BE+AD
(2)DE=BE-AD
(3)DE=AD-BE
同课章节目录
