专题课:带电粒子在有界磁场中的运动练习(含解析)2024-2025学年高二下学期物理人教版(2019)选择性必修 第二册
文档属性
| 名称 | 专题课:带电粒子在有界磁场中的运动练习(含解析)2024-2025学年高二下学期物理人教版(2019)选择性必修 第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 344.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-12 12:29:55 | ||
图片预览


文档简介
专题课:带电粒子在有界磁场中的运动建议用时:40分钟
◆ 知识点一 直线边界
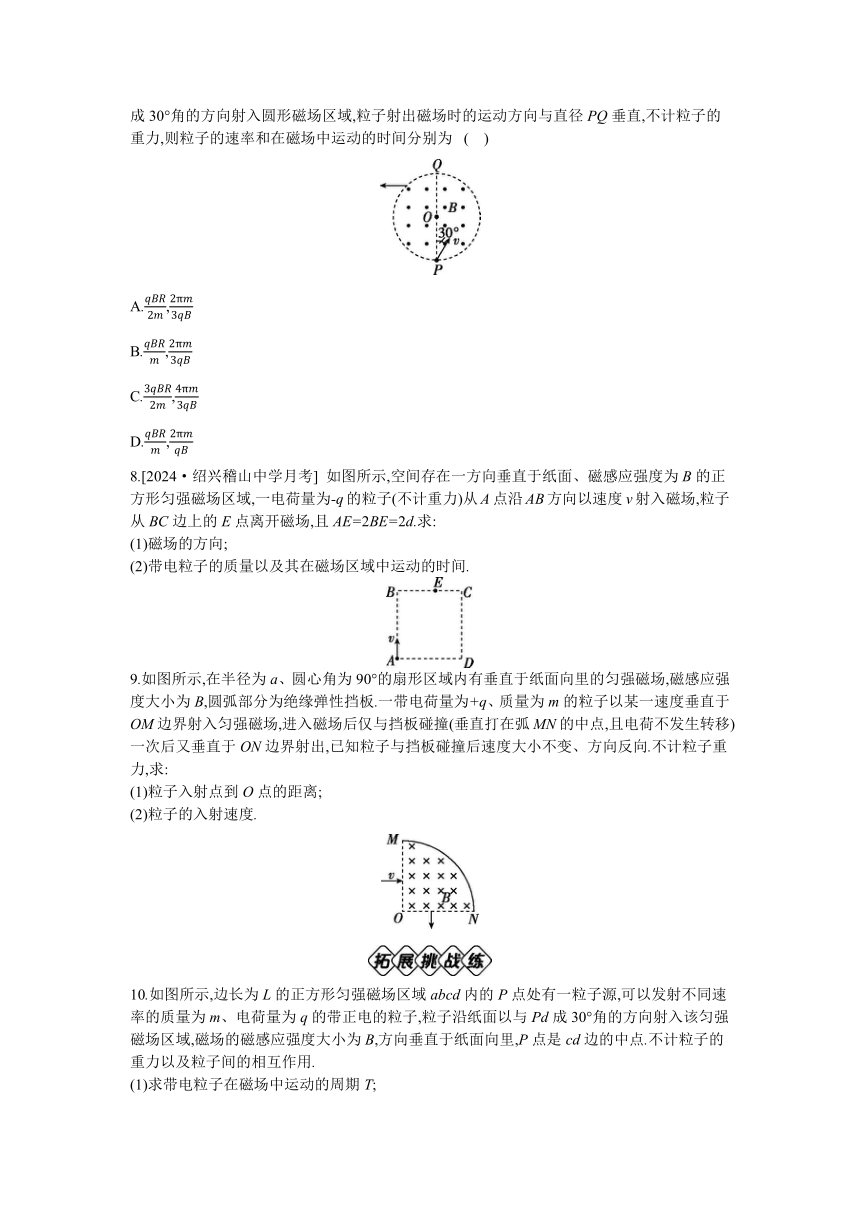
1.如图所示,一条直线上有O、M、N三点,OM=MN,直线上方的整个空间存在垂直于纸面向外的匀强磁场.质子H)和α粒子He)分别以速度v1、v2从O点沿OP方向射入磁场,质子经时间t1从M点射出磁场,α粒子经时间t2从N点射出磁场.质子和α粒子的重力不计,不考虑它们之间的相互作用,则下列判断正确的是( )
A.t1=t2,v1=v2
B.t1C.t1D.t1>t2,v1>v2
2.(不定项)[2024·温州瓯海中学期中] 三个速度大小不同而质量相同的一价离子分别从长方形区域的匀强磁场上边缘的同一位置平行于磁场边界射入磁场,它们从下边缘飞出时的速度方向如图所示,以下判断正确的是( )
A.三个离子均带负电
B.三个离子均带正电
C.离子1在磁场中运动的轨迹半径最大
D.离子3在磁场中运动的时间最短
◆ 知识点二 圆弧边界
3.两个质量相等、带电荷量也相等的带电粒子a、b以不同的速率沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图所示.若不计粒子的重力,则下列说法正确的是( )
A.a粒子带正电,b粒子带负电
B.a粒子在磁场中所受的洛伦兹力较大
C.b粒子的动能较大
D.b粒子在磁场中运动的时间较长
4.[2024·杭州萧山中学月考] 如图所示,圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度v从A点沿直径AOB方向射入
磁场,经过Δt时间从C点射出磁场,OC与OB成60°角.现将带电粒子的速度变为,仍从A点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为( )
A.Δt B.2Δt C.Δt D.3Δt
5.(不定项)如图所示,矩形ABCD区域内有垂直于纸面向里的匀强磁场,AB=2d,BC=d,E为AB中点.从E点沿垂直于AB方向射入粒子a,粒子a经磁场偏转后从D点出磁场,若仍从E点沿垂直于AB方向射入粒子b,粒子b经磁场偏转后从B点出磁场,已知a、b粒子的质量相等,电荷量也相等,不计粒子的重力,则( )
A.a、b粒子均带正电
B.a、b粒子在磁场中做圆周运动的半径之比为4∶1
C.a、b粒子在磁场中运动的速率之比为2∶1
D.a、b粒子在磁场中运动的时间之比为1∶3
6.[2024·台州温岭中学月考] 如图所示,正六边形abcdef区域内有垂直于纸面向外的匀强磁场.一带电粒子从a点沿ad方向射入磁场,粒子从b点离开磁场,
在磁场里的运动时间为t1;如果只改变粒子射入磁场的速度大小,粒子从c点离开磁场,在磁场里的运动时间为t2,不计粒子重力,则t1与t2之比为 ( )
A.1∶2 B.2∶1 C.1∶3 D.3∶1
7.[2024·宁波象山中学期中] 如图所示,匀强磁场区域的横截面为圆形,其半径为R,磁感应强度大小为B,方向垂直于纸面向外.一电荷量为-q(q>0)、质量为m的粒子自P点沿与直径PQ成30°角的方向射入圆形磁场区域,粒子射出磁场时的运动方向与直径PQ垂直,不计粒子的重力,则粒子的速率和在磁场中运动的时间分别为 ( )
A.,
B.,
C.,
D.,
8.[2024·绍兴稽山中学月考] 如图所示,空间存在一方向垂直于纸面、磁感应强度为B的正方形匀强磁场区域,一电荷量为-q的粒子(不计重力)从A点沿AB方向以速度v射入磁场,粒子从BC边上的E点离开磁场,且AE=2BE=2d.求:
(1)磁场的方向;
(2)带电粒子的质量以及其在磁场区域中运动的时间.
9.如图所示,在半径为a、圆心角为90°的扇形区域内有垂直于纸面向里的匀强磁场,磁感应强度大小为B,圆弧部分为绝缘弹性挡板.一带电荷量为+q、质量为m的粒子以某一速度垂直于OM边界射入匀强磁场,进入磁场后仅与挡板碰撞(垂直打在弧MN的中点,且电荷不发生转移)一次后又垂直于ON边界射出,已知粒子与挡板碰撞后速度大小不变、方向反向.不计粒子重力,求:
(1)粒子入射点到O点的距离;
(2)粒子的入射速度.
10.如图所示,边长为L的正方形匀强磁场区域abcd内的P点处有一粒子源,可以发射不同速率的质量为m、电荷量为q的带正电的粒子,粒子沿纸面以与Pd成30°角的方向射入该匀强磁场区域,磁场的磁感应强度大小为B,方向垂直于纸面向里,P点是cd边的中点.不计粒子的重力以及粒子间的相互作用.
(1)求带电粒子在磁场中运动的周期T;
(2)若粒子由边界cd离开磁场,求该粒子在磁场中运动的时间t;
(3)若粒子离开磁场时的速度方向偏转了120°,求该粒子的速度大小v.
专题课:带电粒子在有界磁场中的运动
1.B [解析] 粒子运动轨迹如图所示,设OM=MN=L,对质子,根据洛伦兹力提供向心力,有q1v1B=m1,解得r1=,根据几何关系得2r1sin θ=L,联立得v1=,对α粒子,同理可得v2=,由题意可知m2=4m1,q2=2q1,联立可得v1=v2,质子运动的周期为T1=,α粒子运动的周期为T2=,可得T2>T1,因为运动轨迹对应的圆心角相等,所以t2>t1,故B正确.
2.AD [解析] 根据左手定则可知,三个离子均带负电,选项A正确,B错误;画出三个离子运动的轨迹如图所示,由图可知,离子1的轨迹半径最小,离子3的轨迹半径最大,选项C错误;三个离子运动的周期均为T=,则运动时间t=T,由图可知,离子1运动轨迹对应的圆心角最大,离子3运动轨迹对应的圆心角最小,所以离子1在磁场中运动的时间最长,离子3在磁场中运动的时间最短,选项D正确.
3.C [解析] 由左手定则可判定a粒子带负电,b粒子带正电,由于b粒子运动的半径大,故b粒子的速率大,动能大,所受的洛伦兹力大,选项C正确,A、B错误;由题图可知,b粒子运动轨迹所对的圆心角比a粒子小,所以b粒子在磁场中运动的时间较短,选项D错误.
4.B [解析] 带电粒子在匀强磁场中做匀速圆周运动,由洛伦兹力提供向心力,即qvB=m,解得粒子第一次在磁场中运动的半径为r=,如图所示,由几何关系可知,圆弧 AC对应的圆心角∠AO' C=60°,经历的时间为Δt=T(T为粒子在匀强磁场中运动的周期,大小为T=,与粒子速度大小无关),当粒子速度减小为后,根据r=知其在磁场中运动的半径变为,粒子将从D点射出,根据几何关系得圆弧AD对应的圆心角∠AO″ D=120°,经历的时间为Δt'=T=2Δt,选项B正确.
5.BD [解析] 根据左手定则判断可知,a粒子带正电,b粒子带负电,A错误;在磁场中,洛伦兹力提供向心力,粒子的运动轨迹如图所示,对a粒子,由几何知识可得(Ra-d)2+(d)2=,解得Ra=2d,由图可知b粒子在磁场中做圆周运动的半径为Rb=d,则a、b粒子在磁场中做圆周运动的半径之比为4∶1,B正确;在磁场中,洛伦兹力提供向心力,根据qvB=m,可得v=,由于a、b粒子的质量相等,电荷量也相等,则a、b粒子在磁场中运动的速率大小之比为4∶1,C错误;根据T=可知,两粒子的运动周期相同,由几何关系知,a粒子运动轨迹对应的圆心角为,b粒子运动轨迹对应的圆心角为π,根据t=T可得,a、b粒子在磁场中运动的时间之比为1∶3,D正确.
6.B [解析] 当粒子从a点进入磁场,从b点出磁场时,速度偏转角为120°,所以轨迹对应的圆心角为120°,可得粒子在磁场中的运动时间为;当粒子从a点进入磁场,从c点出磁场时,速度偏转角为60°,所以轨迹对应的圆心角为60°,可得粒子在磁场中的运动时间为,因此t1∶t2=2∶1,故选项B正确.
7.B [解析] 根据题意作图,连接MO如图所示,根据几何关系可知四边形O'MOP为菱形,所以粒子的运动半径与磁场半径相等,洛伦兹力提供向心力,有qvB=m,解得v=,粒子在磁场中转过的圆心角∠MO'P=120°,运动的时间为t=T=·=,B正确.
8.(1)垂直于纸面向里 (2)
[解析] (1)粒子沿弧AE运动,洛伦兹力指向弧线内侧,由左手定则可判断出磁场的方向垂直于纸面向里.
(2)如图所示,连接A、E,作线段AE的中垂线,交AD的延长线于O点,O即为粒子运动轨迹的圆心,α为弦切角,因AE=2BE=2d,所以α=30°.
因为圆弧轨迹的圆心角θ=2α=60°,所以△AOE为等边三角形,R=2d
由qvB=m,解得m=
周期T==,所以粒子在磁场区域中运动的时间t==.
9.(1)(-1)a (2)
[解析] (1)根据运动的对称性可知,粒子在碰撞挡板前的运动轨迹与碰撞后的轨迹完全对称,作出运动轨迹如图所示
设粒子运动轨迹的半径为r,由几何关系可得r=a
入射点到O的距离为d=r-r
即d=(-1)a
(2)由洛伦兹力提供向心力可得
qvB=m
解得v=
10.(1) (2) (3)
[解析] (1)粒子在磁场中做匀速圆周运动过程中,由牛顿第二定律有
qvB=m
根据圆周运动的周期公式T=
联立解得T=
(2)根据题意,画出粒子的运动轨迹,如图甲所示
由图可知,若粒子由边界cd离开磁场,则运动轨迹所对的圆心角为θ=π
运动的时间t=T
联立可得t=
(3)根据题意可知,带电粒子在磁场中运动的圆心角为120°,则弦切角与速度方向成60°角,根据几何关系,过P点作cd边的垂线,与ab边交点为Q,则粒子从ab边界中点Q离开磁场,运动轨迹如图乙所示
由几何关系可知rsin 60°=L
解得r=L
根据牛顿第二定律有
qvB=m
解得v=
◆ 知识点一 直线边界
1.如图所示,一条直线上有O、M、N三点,OM=MN,直线上方的整个空间存在垂直于纸面向外的匀强磁场.质子H)和α粒子He)分别以速度v1、v2从O点沿OP方向射入磁场,质子经时间t1从M点射出磁场,α粒子经时间t2从N点射出磁场.质子和α粒子的重力不计,不考虑它们之间的相互作用,则下列判断正确的是( )
A.t1=t2,v1=v2
B.t1
2.(不定项)[2024·温州瓯海中学期中] 三个速度大小不同而质量相同的一价离子分别从长方形区域的匀强磁场上边缘的同一位置平行于磁场边界射入磁场,它们从下边缘飞出时的速度方向如图所示,以下判断正确的是( )
A.三个离子均带负电
B.三个离子均带正电
C.离子1在磁场中运动的轨迹半径最大
D.离子3在磁场中运动的时间最短
◆ 知识点二 圆弧边界
3.两个质量相等、带电荷量也相等的带电粒子a、b以不同的速率沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图所示.若不计粒子的重力,则下列说法正确的是( )
A.a粒子带正电,b粒子带负电
B.a粒子在磁场中所受的洛伦兹力较大
C.b粒子的动能较大
D.b粒子在磁场中运动的时间较长
4.[2024·杭州萧山中学月考] 如图所示,圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度v从A点沿直径AOB方向射入
磁场,经过Δt时间从C点射出磁场,OC与OB成60°角.现将带电粒子的速度变为,仍从A点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为( )
A.Δt B.2Δt C.Δt D.3Δt
5.(不定项)如图所示,矩形ABCD区域内有垂直于纸面向里的匀强磁场,AB=2d,BC=d,E为AB中点.从E点沿垂直于AB方向射入粒子a,粒子a经磁场偏转后从D点出磁场,若仍从E点沿垂直于AB方向射入粒子b,粒子b经磁场偏转后从B点出磁场,已知a、b粒子的质量相等,电荷量也相等,不计粒子的重力,则( )
A.a、b粒子均带正电
B.a、b粒子在磁场中做圆周运动的半径之比为4∶1
C.a、b粒子在磁场中运动的速率之比为2∶1
D.a、b粒子在磁场中运动的时间之比为1∶3
6.[2024·台州温岭中学月考] 如图所示,正六边形abcdef区域内有垂直于纸面向外的匀强磁场.一带电粒子从a点沿ad方向射入磁场,粒子从b点离开磁场,
在磁场里的运动时间为t1;如果只改变粒子射入磁场的速度大小,粒子从c点离开磁场,在磁场里的运动时间为t2,不计粒子重力,则t1与t2之比为 ( )
A.1∶2 B.2∶1 C.1∶3 D.3∶1
7.[2024·宁波象山中学期中] 如图所示,匀强磁场区域的横截面为圆形,其半径为R,磁感应强度大小为B,方向垂直于纸面向外.一电荷量为-q(q>0)、质量为m的粒子自P点沿与直径PQ成30°角的方向射入圆形磁场区域,粒子射出磁场时的运动方向与直径PQ垂直,不计粒子的重力,则粒子的速率和在磁场中运动的时间分别为 ( )
A.,
B.,
C.,
D.,
8.[2024·绍兴稽山中学月考] 如图所示,空间存在一方向垂直于纸面、磁感应强度为B的正方形匀强磁场区域,一电荷量为-q的粒子(不计重力)从A点沿AB方向以速度v射入磁场,粒子从BC边上的E点离开磁场,且AE=2BE=2d.求:
(1)磁场的方向;
(2)带电粒子的质量以及其在磁场区域中运动的时间.
9.如图所示,在半径为a、圆心角为90°的扇形区域内有垂直于纸面向里的匀强磁场,磁感应强度大小为B,圆弧部分为绝缘弹性挡板.一带电荷量为+q、质量为m的粒子以某一速度垂直于OM边界射入匀强磁场,进入磁场后仅与挡板碰撞(垂直打在弧MN的中点,且电荷不发生转移)一次后又垂直于ON边界射出,已知粒子与挡板碰撞后速度大小不变、方向反向.不计粒子重力,求:
(1)粒子入射点到O点的距离;
(2)粒子的入射速度.
10.如图所示,边长为L的正方形匀强磁场区域abcd内的P点处有一粒子源,可以发射不同速率的质量为m、电荷量为q的带正电的粒子,粒子沿纸面以与Pd成30°角的方向射入该匀强磁场区域,磁场的磁感应强度大小为B,方向垂直于纸面向里,P点是cd边的中点.不计粒子的重力以及粒子间的相互作用.
(1)求带电粒子在磁场中运动的周期T;
(2)若粒子由边界cd离开磁场,求该粒子在磁场中运动的时间t;
(3)若粒子离开磁场时的速度方向偏转了120°,求该粒子的速度大小v.
专题课:带电粒子在有界磁场中的运动
1.B [解析] 粒子运动轨迹如图所示,设OM=MN=L,对质子,根据洛伦兹力提供向心力,有q1v1B=m1,解得r1=,根据几何关系得2r1sin θ=L,联立得v1=,对α粒子,同理可得v2=,由题意可知m2=4m1,q2=2q1,联立可得v1=v2,质子运动的周期为T1=,α粒子运动的周期为T2=,可得T2>T1,因为运动轨迹对应的圆心角相等,所以t2>t1,故B正确.
2.AD [解析] 根据左手定则可知,三个离子均带负电,选项A正确,B错误;画出三个离子运动的轨迹如图所示,由图可知,离子1的轨迹半径最小,离子3的轨迹半径最大,选项C错误;三个离子运动的周期均为T=,则运动时间t=T,由图可知,离子1运动轨迹对应的圆心角最大,离子3运动轨迹对应的圆心角最小,所以离子1在磁场中运动的时间最长,离子3在磁场中运动的时间最短,选项D正确.
3.C [解析] 由左手定则可判定a粒子带负电,b粒子带正电,由于b粒子运动的半径大,故b粒子的速率大,动能大,所受的洛伦兹力大,选项C正确,A、B错误;由题图可知,b粒子运动轨迹所对的圆心角比a粒子小,所以b粒子在磁场中运动的时间较短,选项D错误.
4.B [解析] 带电粒子在匀强磁场中做匀速圆周运动,由洛伦兹力提供向心力,即qvB=m,解得粒子第一次在磁场中运动的半径为r=,如图所示,由几何关系可知,圆弧 AC对应的圆心角∠AO' C=60°,经历的时间为Δt=T(T为粒子在匀强磁场中运动的周期,大小为T=,与粒子速度大小无关),当粒子速度减小为后,根据r=知其在磁场中运动的半径变为,粒子将从D点射出,根据几何关系得圆弧AD对应的圆心角∠AO″ D=120°,经历的时间为Δt'=T=2Δt,选项B正确.
5.BD [解析] 根据左手定则判断可知,a粒子带正电,b粒子带负电,A错误;在磁场中,洛伦兹力提供向心力,粒子的运动轨迹如图所示,对a粒子,由几何知识可得(Ra-d)2+(d)2=,解得Ra=2d,由图可知b粒子在磁场中做圆周运动的半径为Rb=d,则a、b粒子在磁场中做圆周运动的半径之比为4∶1,B正确;在磁场中,洛伦兹力提供向心力,根据qvB=m,可得v=,由于a、b粒子的质量相等,电荷量也相等,则a、b粒子在磁场中运动的速率大小之比为4∶1,C错误;根据T=可知,两粒子的运动周期相同,由几何关系知,a粒子运动轨迹对应的圆心角为,b粒子运动轨迹对应的圆心角为π,根据t=T可得,a、b粒子在磁场中运动的时间之比为1∶3,D正确.
6.B [解析] 当粒子从a点进入磁场,从b点出磁场时,速度偏转角为120°,所以轨迹对应的圆心角为120°,可得粒子在磁场中的运动时间为;当粒子从a点进入磁场,从c点出磁场时,速度偏转角为60°,所以轨迹对应的圆心角为60°,可得粒子在磁场中的运动时间为,因此t1∶t2=2∶1,故选项B正确.
7.B [解析] 根据题意作图,连接MO如图所示,根据几何关系可知四边形O'MOP为菱形,所以粒子的运动半径与磁场半径相等,洛伦兹力提供向心力,有qvB=m,解得v=,粒子在磁场中转过的圆心角∠MO'P=120°,运动的时间为t=T=·=,B正确.
8.(1)垂直于纸面向里 (2)
[解析] (1)粒子沿弧AE运动,洛伦兹力指向弧线内侧,由左手定则可判断出磁场的方向垂直于纸面向里.
(2)如图所示,连接A、E,作线段AE的中垂线,交AD的延长线于O点,O即为粒子运动轨迹的圆心,α为弦切角,因AE=2BE=2d,所以α=30°.
因为圆弧轨迹的圆心角θ=2α=60°,所以△AOE为等边三角形,R=2d
由qvB=m,解得m=
周期T==,所以粒子在磁场区域中运动的时间t==.
9.(1)(-1)a (2)
[解析] (1)根据运动的对称性可知,粒子在碰撞挡板前的运动轨迹与碰撞后的轨迹完全对称,作出运动轨迹如图所示
设粒子运动轨迹的半径为r,由几何关系可得r=a
入射点到O的距离为d=r-r
即d=(-1)a
(2)由洛伦兹力提供向心力可得
qvB=m
解得v=
10.(1) (2) (3)
[解析] (1)粒子在磁场中做匀速圆周运动过程中,由牛顿第二定律有
qvB=m
根据圆周运动的周期公式T=
联立解得T=
(2)根据题意,画出粒子的运动轨迹,如图甲所示
由图可知,若粒子由边界cd离开磁场,则运动轨迹所对的圆心角为θ=π
运动的时间t=T
联立可得t=
(3)根据题意可知,带电粒子在磁场中运动的圆心角为120°,则弦切角与速度方向成60°角,根据几何关系,过P点作cd边的垂线,与ab边交点为Q,则粒子从ab边界中点Q离开磁场,运动轨迹如图乙所示
由几何关系可知rsin 60°=L
解得r=L
根据牛顿第二定律有
qvB=m
解得v=
