第一章 勾股定理 单元测试(含答案) 2024-2025学年北师大版八年级数学上册
文档属性
| 名称 | 第一章 勾股定理 单元测试(含答案) 2024-2025学年北师大版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 398.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 11:17:57 | ||
图片预览

文档简介
第一章 勾股定理 单元测试 2024-2025学年北师大版八年级数学上册
一、单选题
1.以下列各组数为边长,能构成直角三角形的是( )
A. B. C. D.
2.如图,小明用探测器探明在A点地下处(即C点)有一贵重物品,由于A点地面下有障碍物,不能垂直下挖,现从距离A点的B点斜着挖掘,则要找到该贵重物品至少要挖( )
A. B. C. D.
3.如图,有一个圆柱形油罐,其底面周长是12m,高AB为5m,现在要以点A为起点环绕油罐表面建梯子,终点正好建在点A的正上方的点B处,则梯子最短需要( )
A.10米 B.11米 C.12米 D.13米
4.直角三角形的两条直角边分别为6,8,则该直角三角形的斜边长为( )
A.4 B. C.10 D.12
5.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连结BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
6.如果线段 能构成直角三角形,则它的比可能是( )
A. B. C. D.
7.若直角三角形两条直角边的边长分别为 cm和 cm,那么此直角三角形斜边长是( )
A.3 cm B.3 cm C.9cm D.27cm
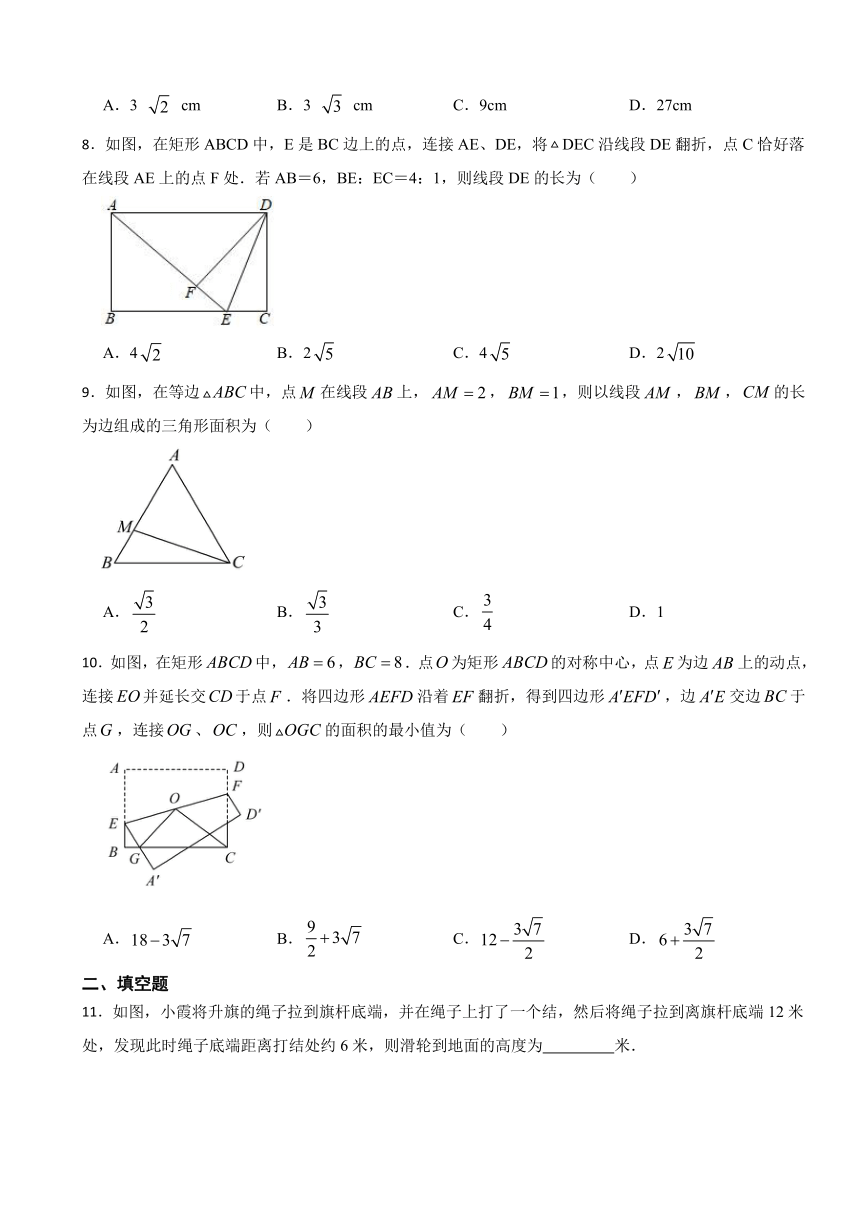
8.如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE:EC=4:1,则线段DE的长为( )
A.4 B.2 C.4 D.2
9.如图,在等边中,点在线段上,,,则以线段,,的长为边组成的三角形面积为( )
A. B. C. D.1
10.如图,在矩形中,,.点为矩形的对称中心,点为边上的动点,连接并延长交于点.将四边形沿着翻折,得到四边形,边交边于点,连接、,则的面积的最小值为( )
A. B. C. D.
二、填空题
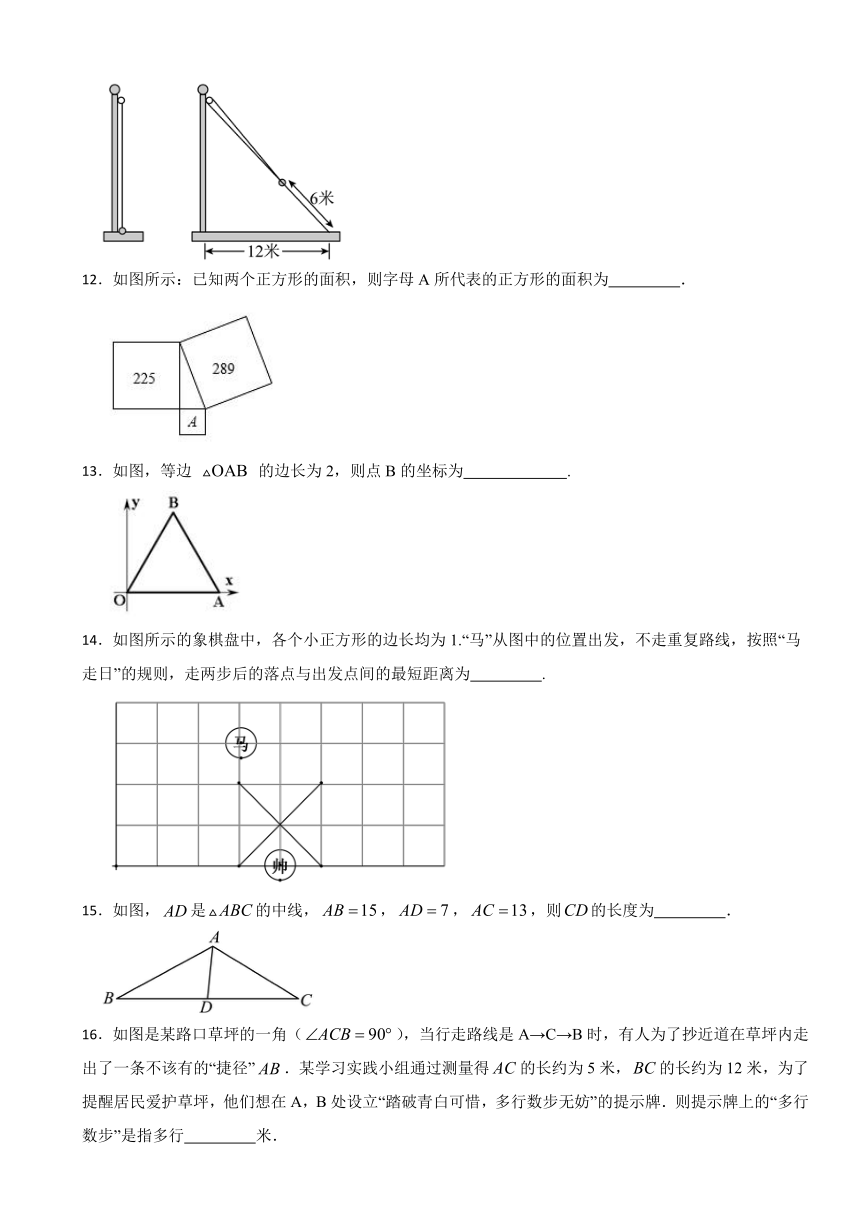
11.如图,小霞将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约6米,则滑轮到地面的高度为 米.
12.如图所示:已知两个正方形的面积,则字母A所代表的正方形的面积为 .
13.如图,等边 的边长为2,则点B的坐标为 .
14.如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为 .
15.如图,是的中线,,,,则的长度为 .
16.如图是某路口草坪的一角(),当行走路线是A→C→B时,有人为了抄近道在草坪内走出了一条不该有的“捷径”.某学习实践小组通过测量得的长约为5米,的长约为12米,为了提醒居民爱护草坪,他们想在A,B处设立“踏破青白可惜,多行数步无妨”的提示牌.则提示牌上的“多行数步”是指多行 米.
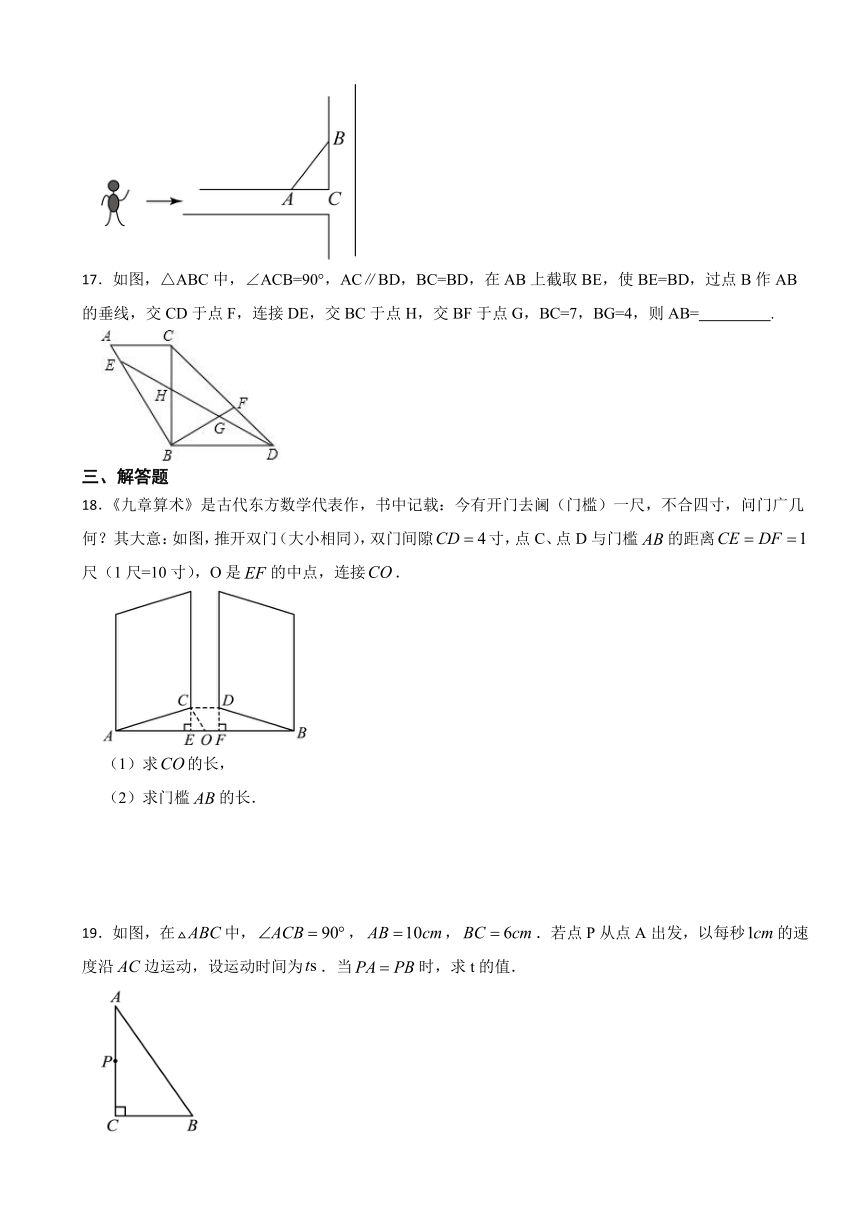
17.如图,△ABC中,∠ACB=90°,AC∥BD,BC=BD,在AB上截取BE,使BE=BD,过点B作AB的垂线,交CD于点F,连接DE,交BC于点H,交BF于点G,BC=7,BG=4,则AB= .
三、解答题
18.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙寸,点C、点D与门槛的距离尺(1尺=10寸),O是的中点,连接.
(1)求的长,
(2)求门槛的长.
19.如图,在中,,,.若点P从点A出发,以每秒的速度沿边运动,设运动时间为.当时,求t的值.
20.如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处,已知AC=6,BC=8,求线段AD的长度.
21.如图,为了测量池塘的宽度DE,在池塘周围的平地上选择了A、B、C三点,且A、D、E、C四点在同一条直线上,∠C=90°,已测得AB=100m,BC=60m,AD=20m,EC=10m,求池塘的宽度DE.
22.如图,一高层住宅发生火灾,消防车立即赶到距大厦8米(AC的长)处,升起云梯到火灾窗口,云梯AB长17米,云梯底部距地面3米(AE的长),问:发生火灾的住户窗口距离地面有多高(BD的长)?
23.某数学兴趣小组开展图形的折叠实验探究,如图,在矩形纸片ABCD中,,,点E为CD上一动点(不与C,D重合)
(1)如图(1),将沿BE折叠,使得点C的对应点恰好落在AD边上的F处,求DE的长;
(2)如图(2),将沿BE折叠,使得点C的对应点为F,连接DF,当DF取得最小值时,求DE的长;
(3)如图(3),小明准备用上述纸片折叠一种纸飞机,发现其中一个步骤是需将沿BE折叠,使点C的对应点F落在矩形ABCD的对称轴上,在这种情况下,求DE的长.
24.如图,在长方形中,,.延长到点,使,连结.动点从点出发,沿以每秒1个单位的速度向终点运动,设点运动的时间为(秒).
(1)的长为 .
(2)连结,当时,求的值.
(3)连结.
①当是直角三角形时,求的值.
②当是等腰三角形时,直接写出的值.
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】A
10.【答案】D
11.【答案】9
12.【答案】64
13.【答案】(1, )
14.【答案】
15.【答案】
16.【答案】4
17.【答案】
18.【答案】(1)
(2)
19.【答案】
20.【答案】AD=3.
21.【答案】解∶在中,
,
,
=(m),
∴,
(m)
22.【答案】解:由题意可知:,米,米,米;
在中,根据勾股定理,得,
即,,
∴(米)
∴(米);
答:发生火灾的住户窗口距离地面18米.
23.【答案】(1)
(2)
(3)或
24.【答案】(1)5
(2)解:在长方形中,,,
,
,
,
,
;
(3)解:①当时,
在中,,
在中,,
,
,
.
当时,此时点与点重合,
,
.
综上所述,当或时,是直角三角形;
②或5或.
一、单选题
1.以下列各组数为边长,能构成直角三角形的是( )
A. B. C. D.
2.如图,小明用探测器探明在A点地下处(即C点)有一贵重物品,由于A点地面下有障碍物,不能垂直下挖,现从距离A点的B点斜着挖掘,则要找到该贵重物品至少要挖( )
A. B. C. D.
3.如图,有一个圆柱形油罐,其底面周长是12m,高AB为5m,现在要以点A为起点环绕油罐表面建梯子,终点正好建在点A的正上方的点B处,则梯子最短需要( )
A.10米 B.11米 C.12米 D.13米
4.直角三角形的两条直角边分别为6,8,则该直角三角形的斜边长为( )
A.4 B. C.10 D.12
5.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连结BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
6.如果线段 能构成直角三角形,则它的比可能是( )
A. B. C. D.
7.若直角三角形两条直角边的边长分别为 cm和 cm,那么此直角三角形斜边长是( )
A.3 cm B.3 cm C.9cm D.27cm
8.如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE:EC=4:1,则线段DE的长为( )
A.4 B.2 C.4 D.2
9.如图,在等边中,点在线段上,,,则以线段,,的长为边组成的三角形面积为( )
A. B. C. D.1
10.如图,在矩形中,,.点为矩形的对称中心,点为边上的动点,连接并延长交于点.将四边形沿着翻折,得到四边形,边交边于点,连接、,则的面积的最小值为( )
A. B. C. D.
二、填空题
11.如图,小霞将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约6米,则滑轮到地面的高度为 米.
12.如图所示:已知两个正方形的面积,则字母A所代表的正方形的面积为 .
13.如图,等边 的边长为2,则点B的坐标为 .
14.如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为 .
15.如图,是的中线,,,,则的长度为 .
16.如图是某路口草坪的一角(),当行走路线是A→C→B时,有人为了抄近道在草坪内走出了一条不该有的“捷径”.某学习实践小组通过测量得的长约为5米,的长约为12米,为了提醒居民爱护草坪,他们想在A,B处设立“踏破青白可惜,多行数步无妨”的提示牌.则提示牌上的“多行数步”是指多行 米.
17.如图,△ABC中,∠ACB=90°,AC∥BD,BC=BD,在AB上截取BE,使BE=BD,过点B作AB的垂线,交CD于点F,连接DE,交BC于点H,交BF于点G,BC=7,BG=4,则AB= .
三、解答题
18.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙寸,点C、点D与门槛的距离尺(1尺=10寸),O是的中点,连接.
(1)求的长,
(2)求门槛的长.
19.如图,在中,,,.若点P从点A出发,以每秒的速度沿边运动,设运动时间为.当时,求t的值.
20.如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处,已知AC=6,BC=8,求线段AD的长度.
21.如图,为了测量池塘的宽度DE,在池塘周围的平地上选择了A、B、C三点,且A、D、E、C四点在同一条直线上,∠C=90°,已测得AB=100m,BC=60m,AD=20m,EC=10m,求池塘的宽度DE.
22.如图,一高层住宅发生火灾,消防车立即赶到距大厦8米(AC的长)处,升起云梯到火灾窗口,云梯AB长17米,云梯底部距地面3米(AE的长),问:发生火灾的住户窗口距离地面有多高(BD的长)?
23.某数学兴趣小组开展图形的折叠实验探究,如图,在矩形纸片ABCD中,,,点E为CD上一动点(不与C,D重合)
(1)如图(1),将沿BE折叠,使得点C的对应点恰好落在AD边上的F处,求DE的长;
(2)如图(2),将沿BE折叠,使得点C的对应点为F,连接DF,当DF取得最小值时,求DE的长;
(3)如图(3),小明准备用上述纸片折叠一种纸飞机,发现其中一个步骤是需将沿BE折叠,使点C的对应点F落在矩形ABCD的对称轴上,在这种情况下,求DE的长.
24.如图,在长方形中,,.延长到点,使,连结.动点从点出发,沿以每秒1个单位的速度向终点运动,设点运动的时间为(秒).
(1)的长为 .
(2)连结,当时,求的值.
(3)连结.
①当是直角三角形时,求的值.
②当是等腰三角形时,直接写出的值.
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】A
10.【答案】D
11.【答案】9
12.【答案】64
13.【答案】(1, )
14.【答案】
15.【答案】
16.【答案】4
17.【答案】
18.【答案】(1)
(2)
19.【答案】
20.【答案】AD=3.
21.【答案】解∶在中,
,
,
=(m),
∴,
(m)
22.【答案】解:由题意可知:,米,米,米;
在中,根据勾股定理,得,
即,,
∴(米)
∴(米);
答:发生火灾的住户窗口距离地面18米.
23.【答案】(1)
(2)
(3)或
24.【答案】(1)5
(2)解:在长方形中,,,
,
,
,
,
;
(3)解:①当时,
在中,,
在中,,
,
,
.
当时,此时点与点重合,
,
.
综上所述,当或时,是直角三角形;
②或5或.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
