第一章 特殊平行四边形 单元测试 (含答案)2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 第一章 特殊平行四边形 单元测试 (含答案)2024-2025学年北师大版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 568.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 00:00:00 | ||
图片预览


文档简介
第一章 特殊平行四边形 单元测试 2024-2025学年北师大版九年级数学上册
一、单选题
1.下列命题中,属于假命题的是( )
A.菱形的面积等于两条对角线乘积的一半
B.矩形的对角线相等
C.对角线互相垂直的平行四边形是矩形
D.对角线相等的菱形是正方形
2.定义:一个四边形中,若有一个角的两边相等,且与它的对角互补,则称这个四边形为“半等边四边形”,则下列四边形一定是“半等边四边形”的是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
3.如图,在正方形ABCD中,对角线AC的长为4,则正方形ABCD的面积为( )
A.4 B.8 C.12 D.16
4.如图,在四边形中,对角线,垂足为,点、、、分别为边、、、的中点.若,,则四边形的面积为( )
A.48 B.24 C.32 D.12
5.如图,在正方形中,点F为上的一点,与交于点E.若,则等于( )
A. B. C. D.
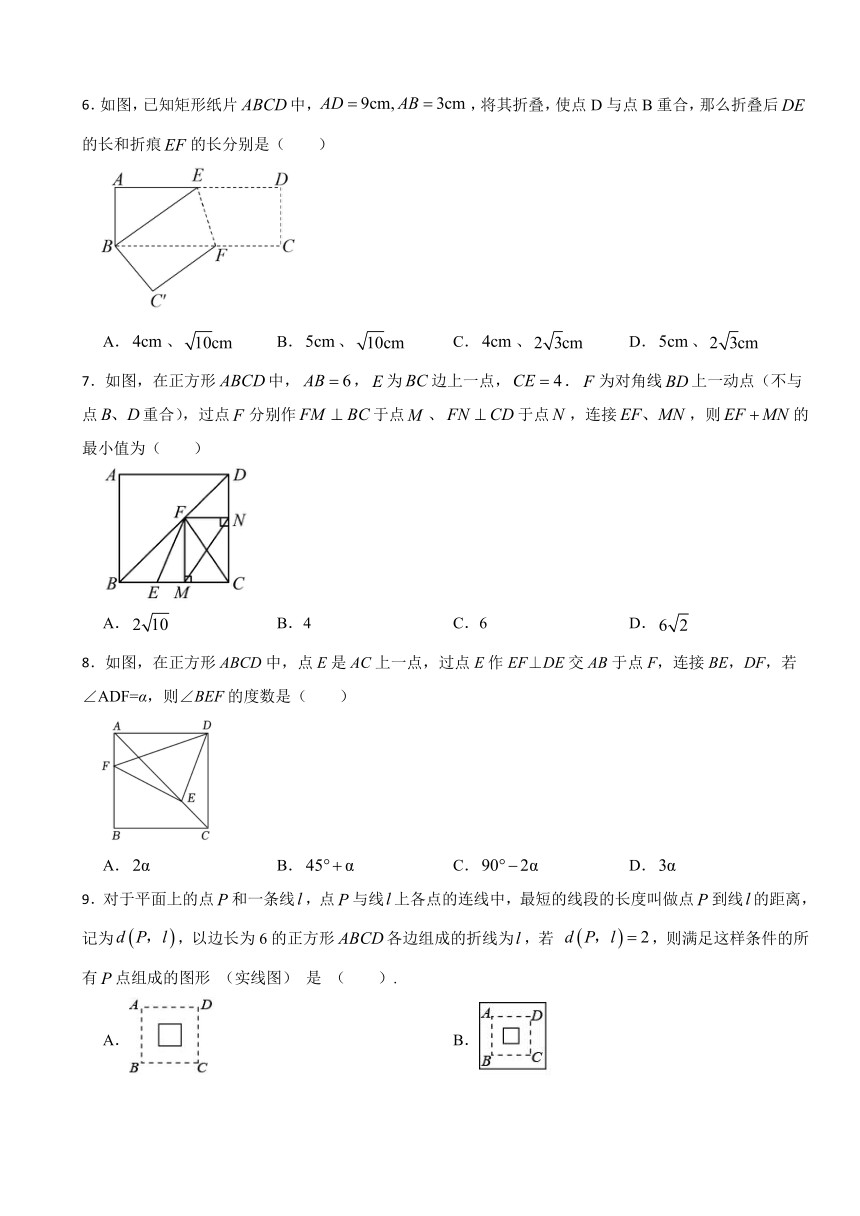
6.如图,已知矩形纸片中,,将其折叠,使点D与点B重合,那么折叠后的长和折痕的长分别是( )
A.、 B.、 C.、 D.、
7.如图,在正方形中,,为边上一点,.为对角线上一动点(不与点重合),过点分别作于点、于点,连接,则的最小值为( )
A. B.4 C.6 D.
8.如图,在正方形ABCD中,点E是AC上一点,过点E作EF⊥DE交AB于点F,连接BE,DF,若∠ADF=α,则∠BEF的度数是( )
A. B. C. D.
9.对于平面上的点和一条线,点与线上各点的连线中,最短的线段的长度叫做点到线的距离,记为,以边长为6的正方形各边组成的折线为,若 ,则满足这样条件的所有点组成的图形 (实线图) 是 ( ).
A. B.
C. D.
10.如图,正方形ABCD中,E是BC延长线上一点,在AB上取一点F,使点B关于直线EF的对称点G落在AD上,连接EG交CD于点H,连接BH交EF于点M,连接CM.则下列结论,其中正确的是( )
①∠1=∠2;
②∠3=∠4;
③GD=CM;
④若AG=1,GD=2,则BM=.
A.①②③④ B.①② C.③④ D.①②④
二、填空题
11.如图,正方形的边长为2,E是的中点,点P是边上的一个动点,连接,,则的最小值为 .
12.如图,在的两边上分别截取,使,分别以点A,B为圆心,长为半径作弧,两弧交于点C,连接,若,四边形的面积为,则的长为 .
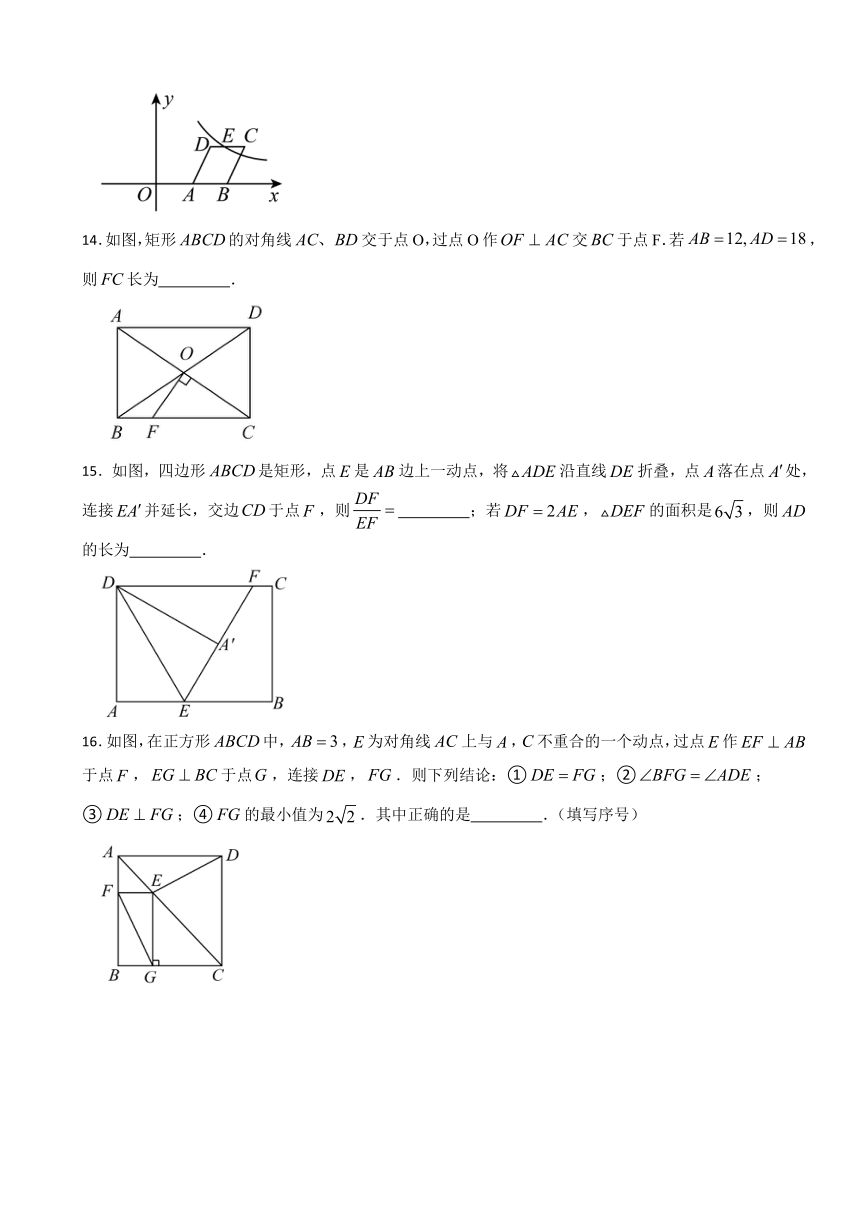
13.如图,把边长为2的菱形放在平面直角坐标系中,边在轴上,,点的坐标是,是边的中点,反比例函数的图象经过点,则的值是 .
14.如图,矩形的对角线交于点O,过点O作交于点F.若,则长为 .
15.如图,四边形是矩形,点是边上一动点,将沿直线折叠,点落在点处,连接并延长,交边于点,则 ;若,的面积是,则的长为 .
16.如图,在正方形中,,为对角线上与,不重合的一个动点,过点作于点,于点,连接,.则下列结论:①;②;③;④的最小值为.其中正确的是 .(填写序号)
三、解答题
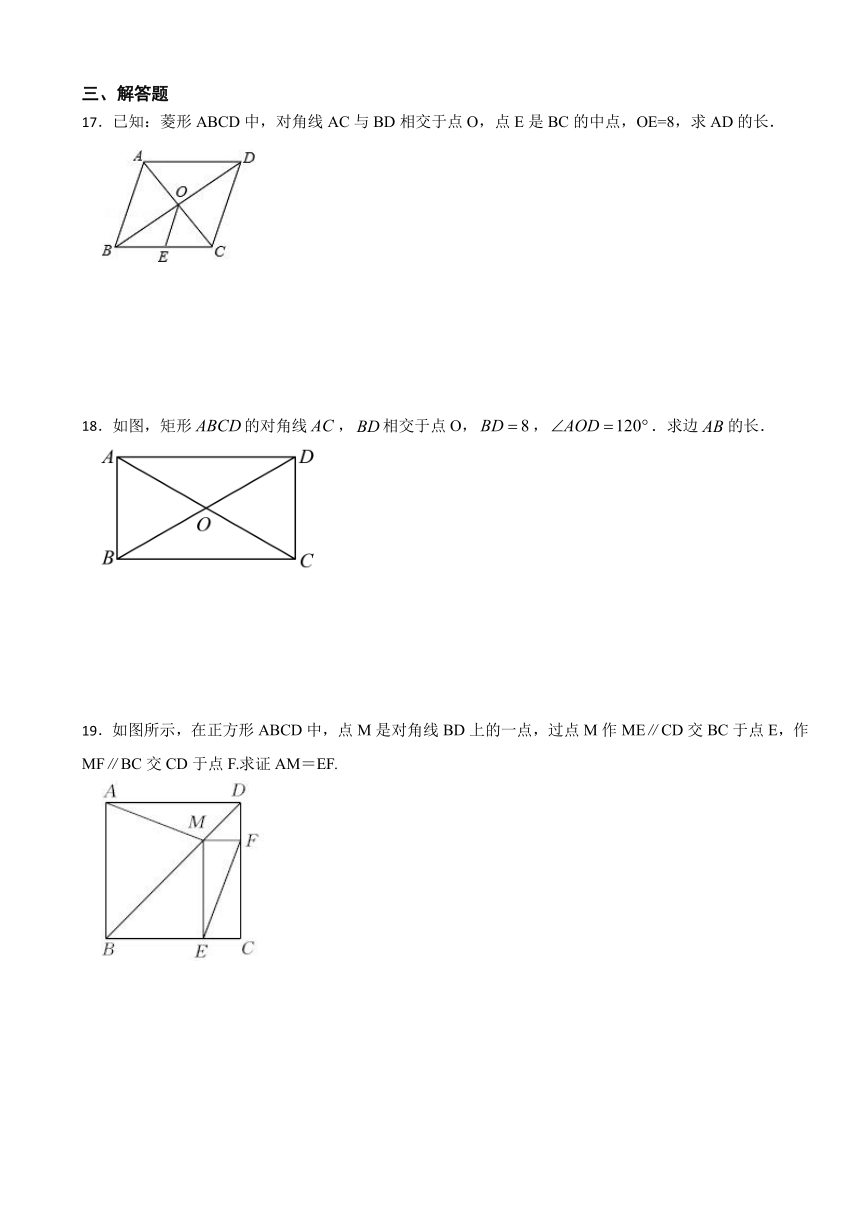
17.已知:菱形ABCD中,对角线AC与BD相交于点O,点E是BC的中点,OE=8,求AD的长.
18.如图,矩形的对角线,相交于点O,,.求边的长.
19.如图所示,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证AM=EF.
20.如图,菱形ABCD中,对角线AC、BD交于点O,CE∥BD,DE∥AC.判断四边形DOCE的形状,并证明.
21.如图,点在的边AD上,,请从以下三个选项中:①;②;③,选择一个合适的选项作为已知条件,使为矩形.
(1)你添加的条件是 (填序号);
(2)添加条件后,请证明为矩形.
22.如图①,在平面直角坐标系中,一次函数的图象与x,y轴分别交于A,B两点,正比例函数的图象与交于点.
(1)求n、k的值;
(2)已知点D是直线:上的一个动点.
①过点D作轴,交直线于点P,当点D,P关于x轴对称时,则点D的横坐标为______;
②连接,当的面积是面积的2倍时,求点D的坐标;
(3)如图②,设点E的坐标为,且,连接,以为边向下作正方形.
①用含t的式子表示点M的坐标为(______,______);
②连接,若落在的内部(含边上),则t的取值范围是______.
23.在△ABC中,AC=BC,点D是边AB上不与点B重合的一动点,将△BDC绕点D旋转得到△EDF,点B的对应点E落在直线BC上,EF与AC相交于点G,连接AF.
(1)如图1,当点D与点A重合时,
①求证:∠C=∠CEF;
②判断AF与BC的位置关系是 ▲ ;
(2)如图2,当点D不与点A重合,点E在边BC上时,判断AF与BC的位置关系,并写出证明过程;
(3)如图3,当点D是AB的中点,点E在边BC上时,延长BA,CF相交于点P,若AB=CD=2,求PF的长.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】
12.【答案】10
13.【答案】
14.【答案】13
15.【答案】1;
16.【答案】①②③
17.【答案】16
18.【答案】4
19.【答案】解:过M点作MQ⊥AD,垂足为Q,作MP⊥AB,垂足为P,
∵四边形ABCD是正方形,
∴四边形MFDQ和四边形PBEM是正方形,四边形APMQ是矩形,
∴AP=QM=DF=MF,PM=PB=ME,
∵在△APM和△FME中,
,
∴△APM≌△FME(SAS),
∴AM=EF.
20.【答案】解:四边形DOCE是矩形.
证明:∵CE∥BD,DE∥AC,
∴四边形CODE为平行四边形.
∵四边形ABCD是菱形,
∴,
∴,
∴四边形DOCE是矩形.
21.【答案】(1)①或②
(2)解:选择①∠1=∠2,
证明:∵BM=CM,
∴∠3=∠4,
∵∠1=∠2,
∴∠ABC=∠BCD,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠ABC=∠BCD=90°,
∴为矩形;
选择②AM=DM,
证明:四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠A+∠D=180°,
在和中,
,
∴,
∴∠A=∠D,
∴∠A=∠D=90°,
为矩形.
22.【答案】(1)n、k的值分别为、;
(2)①;②或
(3)①;②
23.【答案】(1)解:①证明:∵AC=BC,AE=AB,
∴∠CAB=∠B=∠AEB,
∴∠C=180°﹣∠B﹣∠CAB=180°﹣2∠B,
由旋转的性质可得∠FEA=∠B,∠F=∠C,
∴∠CEF=180°﹣∠AEB﹣∠AEF=180°﹣2∠B,
∴∠C=∠CEF;
②AF∥BC;
(2)解:AF∥BC,理由为:
过点F作FH⊥CB于点H,过点A作AK⊥BC于点K,如图,
则∠FHC=∠AKB=90°.
∴FH∥AK,
由旋转可得AC=EF=BC,
由(1)可得∠ACE=∠CEF,
在△FHE和△AKC中,
,
∴△FHE≌△AKC(AAS),
∴FH=AK,
∴四边形AKHF是矩形,
∴AF∥BC;
(3)解:连接AE,如图,
∵点D是AB的中点,
∴AD=DE=DB=1,∠CDB=90°,
∴∠EAD=∠AED,∠EBD=∠DEB,
∴∠AEB=∠AED+∠DEB=∠EAD+∠EBD=90°,
由旋转可得DC=DF,∠FDE=∠CDB=90°,
∴∠FDC=∠EDB.
∴∠FCB=∠FCD+∠DCB=∠B+∠DCB=90°,
由(2)可得四边形AFCE是矩形,
∴CF=AE,AF=CE,AF∥CE,
,
,即,
,
,
∵AF∥CE,
∴△PFA∽△PCB,
,即,
解得.
一、单选题
1.下列命题中,属于假命题的是( )
A.菱形的面积等于两条对角线乘积的一半
B.矩形的对角线相等
C.对角线互相垂直的平行四边形是矩形
D.对角线相等的菱形是正方形
2.定义:一个四边形中,若有一个角的两边相等,且与它的对角互补,则称这个四边形为“半等边四边形”,则下列四边形一定是“半等边四边形”的是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
3.如图,在正方形ABCD中,对角线AC的长为4,则正方形ABCD的面积为( )
A.4 B.8 C.12 D.16
4.如图,在四边形中,对角线,垂足为,点、、、分别为边、、、的中点.若,,则四边形的面积为( )
A.48 B.24 C.32 D.12
5.如图,在正方形中,点F为上的一点,与交于点E.若,则等于( )
A. B. C. D.
6.如图,已知矩形纸片中,,将其折叠,使点D与点B重合,那么折叠后的长和折痕的长分别是( )
A.、 B.、 C.、 D.、
7.如图,在正方形中,,为边上一点,.为对角线上一动点(不与点重合),过点分别作于点、于点,连接,则的最小值为( )
A. B.4 C.6 D.
8.如图,在正方形ABCD中,点E是AC上一点,过点E作EF⊥DE交AB于点F,连接BE,DF,若∠ADF=α,则∠BEF的度数是( )
A. B. C. D.
9.对于平面上的点和一条线,点与线上各点的连线中,最短的线段的长度叫做点到线的距离,记为,以边长为6的正方形各边组成的折线为,若 ,则满足这样条件的所有点组成的图形 (实线图) 是 ( ).
A. B.
C. D.
10.如图,正方形ABCD中,E是BC延长线上一点,在AB上取一点F,使点B关于直线EF的对称点G落在AD上,连接EG交CD于点H,连接BH交EF于点M,连接CM.则下列结论,其中正确的是( )
①∠1=∠2;
②∠3=∠4;
③GD=CM;
④若AG=1,GD=2,则BM=.
A.①②③④ B.①② C.③④ D.①②④
二、填空题
11.如图,正方形的边长为2,E是的中点,点P是边上的一个动点,连接,,则的最小值为 .
12.如图,在的两边上分别截取,使,分别以点A,B为圆心,长为半径作弧,两弧交于点C,连接,若,四边形的面积为,则的长为 .
13.如图,把边长为2的菱形放在平面直角坐标系中,边在轴上,,点的坐标是,是边的中点,反比例函数的图象经过点,则的值是 .
14.如图,矩形的对角线交于点O,过点O作交于点F.若,则长为 .
15.如图,四边形是矩形,点是边上一动点,将沿直线折叠,点落在点处,连接并延长,交边于点,则 ;若,的面积是,则的长为 .
16.如图,在正方形中,,为对角线上与,不重合的一个动点,过点作于点,于点,连接,.则下列结论:①;②;③;④的最小值为.其中正确的是 .(填写序号)
三、解答题
17.已知:菱形ABCD中,对角线AC与BD相交于点O,点E是BC的中点,OE=8,求AD的长.
18.如图,矩形的对角线,相交于点O,,.求边的长.
19.如图所示,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证AM=EF.
20.如图,菱形ABCD中,对角线AC、BD交于点O,CE∥BD,DE∥AC.判断四边形DOCE的形状,并证明.
21.如图,点在的边AD上,,请从以下三个选项中:①;②;③,选择一个合适的选项作为已知条件,使为矩形.
(1)你添加的条件是 (填序号);
(2)添加条件后,请证明为矩形.
22.如图①,在平面直角坐标系中,一次函数的图象与x,y轴分别交于A,B两点,正比例函数的图象与交于点.
(1)求n、k的值;
(2)已知点D是直线:上的一个动点.
①过点D作轴,交直线于点P,当点D,P关于x轴对称时,则点D的横坐标为______;
②连接,当的面积是面积的2倍时,求点D的坐标;
(3)如图②,设点E的坐标为,且,连接,以为边向下作正方形.
①用含t的式子表示点M的坐标为(______,______);
②连接,若落在的内部(含边上),则t的取值范围是______.
23.在△ABC中,AC=BC,点D是边AB上不与点B重合的一动点,将△BDC绕点D旋转得到△EDF,点B的对应点E落在直线BC上,EF与AC相交于点G,连接AF.
(1)如图1,当点D与点A重合时,
①求证:∠C=∠CEF;
②判断AF与BC的位置关系是 ▲ ;
(2)如图2,当点D不与点A重合,点E在边BC上时,判断AF与BC的位置关系,并写出证明过程;
(3)如图3,当点D是AB的中点,点E在边BC上时,延长BA,CF相交于点P,若AB=CD=2,求PF的长.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】A
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】
12.【答案】10
13.【答案】
14.【答案】13
15.【答案】1;
16.【答案】①②③
17.【答案】16
18.【答案】4
19.【答案】解:过M点作MQ⊥AD,垂足为Q,作MP⊥AB,垂足为P,
∵四边形ABCD是正方形,
∴四边形MFDQ和四边形PBEM是正方形,四边形APMQ是矩形,
∴AP=QM=DF=MF,PM=PB=ME,
∵在△APM和△FME中,
,
∴△APM≌△FME(SAS),
∴AM=EF.
20.【答案】解:四边形DOCE是矩形.
证明:∵CE∥BD,DE∥AC,
∴四边形CODE为平行四边形.
∵四边形ABCD是菱形,
∴,
∴,
∴四边形DOCE是矩形.
21.【答案】(1)①或②
(2)解:选择①∠1=∠2,
证明:∵BM=CM,
∴∠3=∠4,
∵∠1=∠2,
∴∠ABC=∠BCD,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠ABC=∠BCD=90°,
∴为矩形;
选择②AM=DM,
证明:四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠A+∠D=180°,
在和中,
,
∴,
∴∠A=∠D,
∴∠A=∠D=90°,
为矩形.
22.【答案】(1)n、k的值分别为、;
(2)①;②或
(3)①;②
23.【答案】(1)解:①证明:∵AC=BC,AE=AB,
∴∠CAB=∠B=∠AEB,
∴∠C=180°﹣∠B﹣∠CAB=180°﹣2∠B,
由旋转的性质可得∠FEA=∠B,∠F=∠C,
∴∠CEF=180°﹣∠AEB﹣∠AEF=180°﹣2∠B,
∴∠C=∠CEF;
②AF∥BC;
(2)解:AF∥BC,理由为:
过点F作FH⊥CB于点H,过点A作AK⊥BC于点K,如图,
则∠FHC=∠AKB=90°.
∴FH∥AK,
由旋转可得AC=EF=BC,
由(1)可得∠ACE=∠CEF,
在△FHE和△AKC中,
,
∴△FHE≌△AKC(AAS),
∴FH=AK,
∴四边形AKHF是矩形,
∴AF∥BC;
(3)解:连接AE,如图,
∵点D是AB的中点,
∴AD=DE=DB=1,∠CDB=90°,
∴∠EAD=∠AED,∠EBD=∠DEB,
∴∠AEB=∠AED+∠DEB=∠EAD+∠EBD=90°,
由旋转可得DC=DF,∠FDE=∠CDB=90°,
∴∠FDC=∠EDB.
∴∠FCB=∠FCD+∠DCB=∠B+∠DCB=90°,
由(2)可得四边形AFCE是矩形,
∴CF=AE,AF=CE,AF∥CE,
,
,即,
,
,
∵AF∥CE,
∴△PFA∽△PCB,
,即,
解得.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
