江苏省徐州市新沂市2014-2015学年高二(下)期中数学试卷(理科)(解析版)
文档属性
| 名称 | 江苏省徐州市新沂市2014-2015学年高二(下)期中数学试卷(理科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 138.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-20 19:39:54 | ||
图片预览




文档简介
2014-2015学年江苏省徐州市新沂市高二(下)期中数学试卷(理科)
一、填空题(本大题共14小题,每小题5分,共计70分。不需要写出解答过程,请把答案直接填写在相应位置上)
1.若复数z=m(m+1)+(m+1)i(i为虚数单位)是纯虚数,则实数m的值为 .
2.“因为自然数是整数(大前提),而是自然数(小前提),所以是整数(结论)”,上面的推理是因为 (填“大前提”或“小前提”)错误导致结论错误.
3.有5本不同的书,从中选2本送给2名同学,每人各一本,共有 (填数字)种不同的送法.
4.设复数z满足i(z+1)=﹣3+2i(i为虚数单位),则z等于 .
5.有如下真命题:“若数列{an}是一个公 ( http: / / www.21cnjy.com )差为d的等差数列,则数列{an+an+1+an+2}是公差为3d的等差数列.”把上述命题类比到等比数列中,可得真命题是“ .”(注:填上你认为可以成为真命题的一种情形即可)
6.已知复数z满足|z+4﹣3i|=2(i为虚数单位).则|z|的最大值为 .
7.设(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n,那么a2+a4+…+a2n= .
8.观察下列各式:13=12,13+23=32,13+23+33=62,13+23+33+43=102,则得到的一般结论是 .
9.设(3+)n的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为 .
10.直线方程Ax+By=0,若从0,1, ( http: / / www.21cnjy.com )2,3,5,6这六个数字中每次取两个不同的数作为系数A、B的值,则方程Ax+By=0所表示的不同直线的条数是 .
11.已知数列{an}(n ( http: / / www.21cnjy.com )∈N*)是首项为2,公比为3的等比数列,则a1C﹣a2C+a3C﹣a4C+a5C﹣a6C+a7C= .
12.用数学归纳法证明结论:(n+1) ( http: / / www.21cnjy.com )(n+2)…(n+n)=2n×1×2×…×(2n﹣1)(n∈N*)时,从“k到k+1”左边需增乘的代数式为 .
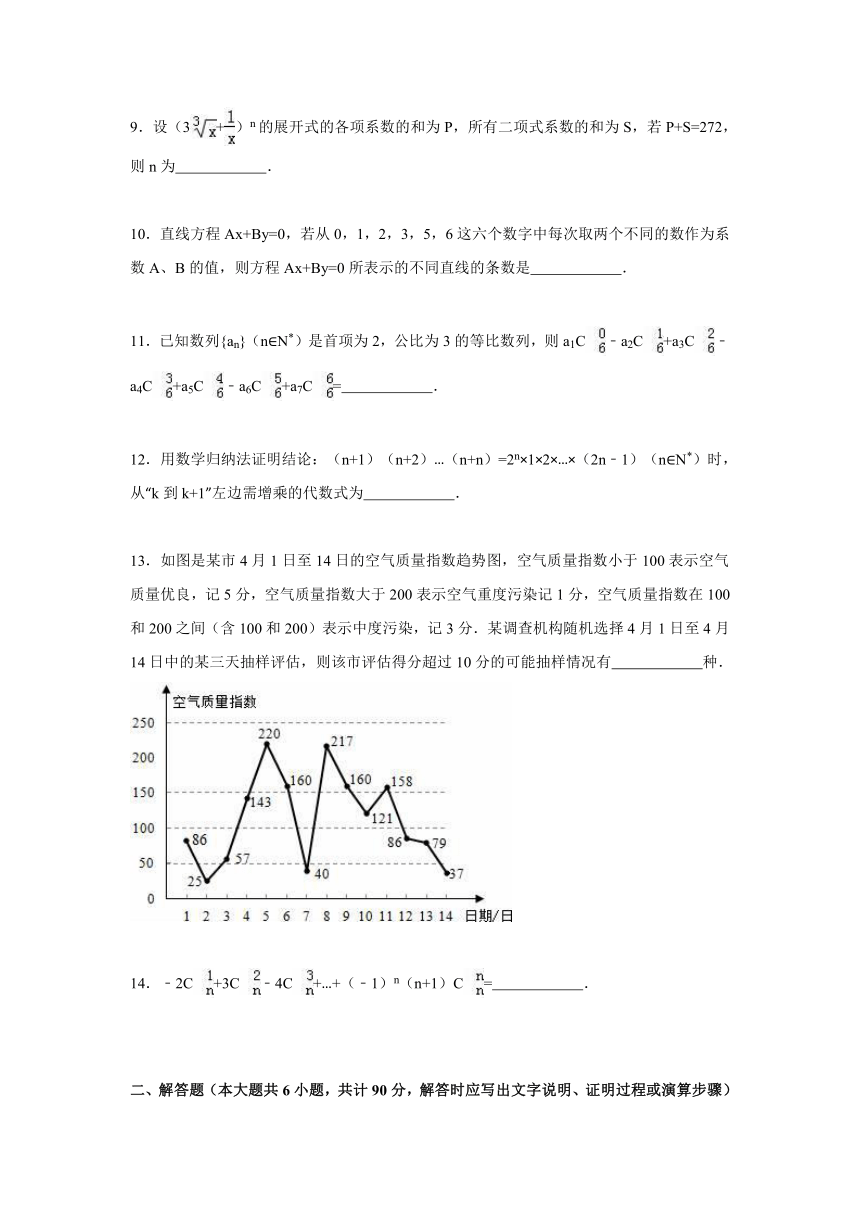
13.如图是某市4月1日至14日的 ( http: / / www.21cnjy.com )空气质量指数趋势图,空气质量指数小于100表示空气质量优良,记5分,空气质量指数大于200表示空气重度污染记1分,空气质量指数在100和200之间(含100和200)表示中度污染,记3分.某调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分的可能抽样情况有 种.
14.﹣2C+3C﹣4C+…+(﹣1)n(n+1)C= .
二、解答题(本大题共6小题,共计90分,解答时应写出文字说明、证明过程或演算步骤)
15.在复平面内,复数2﹣i,1+i,4所对应的点分别是A、B、C,四边形ABCD为平行四边形.
(1)求点D所对应的复数;
(2)求 ABCD的对角线BD的长.
16.已知:a,b,c,(a,b,c∈R)成等比数列,且公比q≠1,求证:1﹣a,1﹣b,1﹣c不可能成等比数列.
17.3名男生,4名女生排成一排,问:
(1)3名男生不相邻,有多少种排法?
(2)甲、乙、丙、丁四人必须站在一起,且甲在乙的左边(不一定相邻),有多少种排法?
(3)甲不在最左边,乙不在最右边,有多少排法?
18.已知在(﹣)n(n∈N*)的展开式中,第6项为常数项.
(1)求n的值及展开式中含x2的项的系数;
(2)①求展开式中所有有理项;
②求展开式中系数的绝对值最大的项.
19.设函数f(x)=ax2+bx+c(a,b,c∈R).
(1)若f(1)=0,a>b>c,求证:<a.
(2)若f(1)=﹣,3a>2c>2b,求证:
①a>0,且﹣3<<﹣;
②函数f(x)在区间(0,2)内至少有一个零点.
20.已知数列{an}是等差数列,(1+)m(m∈N*)展开式的前三项的系数分别为a1,a2,a3.
(1)求(1+)m(m∈N*)的展开式中二项式系数最大的项;
(2)当n≥2(n∈N*)时,试猜测+++…+与的大小并证明.
2014-2015学年江苏省徐州市新沂市高二(下)期中数学试卷(理科)
参考答案与试题解析
一、填空题(本大题共14小题,每小题5分,共计70分。不需要写出解答过程,请把答案直接填写在相应位置上)
1.若复数z=m(m+1)+(m+1)i(i为虚数单位)是纯虚数,则实数m的值为 0 .
【考点】复数的基本概念.
【专题】数系的扩充和复数.
【分析】根据复数为纯虚数的概念,得到复数的实部为0,并且虚部不为0求出m.
【解答】解:因为复数z=m(m+1)+(m+1)i(i为虚数单位)是纯虚数,所以,解得m=0;
故答案为:0.
【点评】本题考查了复数的基本概念;如果复数a+bi(a,b是实数)是纯虚数,那么a=0并且b≠0.
2.“因为自然数是整数(大前提), ( http: / / www.21cnjy.com )而是自然数(小前提),所以是整数(结论)”,上面的推理是因为 小前提 (填“大前提”或“小前提”)错误导致结论错误.
【考点】演绎推理的意义.
【专题】推理和证明.
【分析】要分析一个演绎推理是否正确,主要观察 ( http: / / www.21cnjy.com )所给的大前提,小前提和结论及推理形式是否都正确,根据这几个方面都正确,才能得到这个演绎推理正确.
【解答】解:“因为自然数是整数(大前提),而是自然数(小前提),所以是整数(结论)”,
大前提是:自然数是整数,正确;
小前提是:是自然数,错误,
故导致结论错误的原因是小前提错误,
故答案为:小前提;
【点评】本题考查演绎推理,考查学生分析解决问题的能力,属于基础题
3.有5本不同的书,从中选2本送给2名同学,每人各一本,共有 20 (填数字)种不同的送法.
【考点】计数原理的应用.
【专题】排列组合.
【分析】根据题意,分析可得本题为排列问题,只需从5本不同的书中顺序选出2本,对应送给2位同学即可,由排列数公式计算可得答案
【解答】解:根据题意,只需从5本不同的书中顺序选出2本,对应送给2位同学即可,
有A52=20种方法;
故答案为:20.
【点评】本题考查排列的应用,解题时要首先要分析题意,明确是排列,还是组合问题.
4.设复数z满足i(z+1)=﹣3+2i(i为虚数单位),则z等于 1+3i .
【考点】复数相等的充要条件.
【分析】根据复数相等的条件,即可得到结论.
【解答】解:设z=a+bi,
则由i(z+1)=﹣3+2i得i(a+bi+1)=﹣3+2i=(a+1)i﹣b,
即,解得a=1,b=3,
故z=1+3i,
故答案为:1+3i
【点评】本题主要考查复数的求解,根据复数相等的条件,建立条件关系是解决本题的关键.
5.有如下真命题:“若数列 ( http: / / www.21cnjy.com ){an}是一个公差为d的等差数列,则数列{an+an+1+an+2}是公差为3d的等差数列.”把上述命题类比到等比数列中,可得真命题是“ 若数列{bn}是公比为q的等比数列,则数列{bn bn+1 bn+2}是公比为q3的等比数列;或填为:若数列{bn}是公比为q的等比数列,则数列{bn+bn+1+bn+2}是公比为q的等比数列 .”(注:填上你认为可以成为真命题的一种情形即可)
【考点】归纳推理.
【专题】开放型.
【分析】是一个类比推理的 ( http: / / www.21cnjy.com )问题,在类比推理中,等差数列到等比数列的类比推理方法一般为:加减运算类比推理为乘除运算,累加类比为累乘,由:“若数列{an}是一个公差为d的等差数列,则数列{an+an+1+an+2}是公差为3d的等差数列.”类比推理得:“若数列{bn}是公比为q的等比数列,则数列{bn bn+1 bn+2}是公比为q3的等比数列;或:若数列{bn}是公比为q的等比数列,则数列{bn+bn+1+bn+2}是公比为q的等比数列”
【解答】解:由等差数列的性质类比推理等比数列的性质时
类比推理方法一般为:
加减运算类比推理为乘除运算,
累加类比为累乘,
由:“若数列{an}是一个公差为d的等差数列,则数列{an+an+1+an+2}是公差为3d的等差数列.”
类比推理得:
“若数列{bn}是公比为q的等比数列,则数列{bn bn+1 bn+2}是公比为q3的等比数列;”
或“若数列{bn}是公比为q的等比数列,则数列{bn+bn+1+bn+2}是公比为q的等比数列”
故答案:若数列{bn}是公比为q的等比 ( http: / / www.21cnjy.com )数列,则数列{bn bn+1 bn+2}是公比为q3的等比数列;或填为:若数列{bn}是公比为q的等比数列,则数列{bn+bn+1+bn+2}是公比为q的等比数列.
【点评】类比推理的一般步骤是:(1)找 ( http: / / www.21cnjy.com )出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).
6.已知复数z满足|z+4﹣3i|=2(i为虚数单位).则|z|的最大值为 7 .
【考点】复数的代数表示法及其几何意义.
【分析】利用不等式|a|﹣|b|≤|a±b|≤|a|+|b|即可得出结论.
【解答】解:∵复数z满足|z+4﹣3i|=2(i为虚数单位),
∴|z+(4﹣3i)|=2,
∴|z|﹣|4﹣3i|≤|z+(4﹣3i)|=2,
∴|z|≤2+|4﹣3i|=2+5=7,
∴|z|的最大值为7.
故答案为:7.
【点评】本题考查了复数的代数运算与几何意义的应用问题,是基础题目.
7.设(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n,那么a2+a4+…+a2n= .
【考点】二项式系数的性质.
【专题】二项式定理.
【分析】在所给的等式中,令x=0求 ( http: / / www.21cnjy.com )得a0=1,再分别令x=1、x=﹣1,可得2个式子,再把这2个式子相加,变形即可求得a2+a4+…+a2n的值.
【解答】解:在(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n中,令x=0可得a0=1.
令x=1,可得 a0+a1+a2+a3+…+a2n﹣1+a2n=3n,
再令x=﹣1可得a0﹣a1+a2﹣a3+…﹣a2n﹣1+a2n=1,
再把这两个等式相加可得2(a0+a2+a4+…+a2n)=3n+1,
由此可得a2+a4+…+a2n=,
故答案为:.
【点评】本题主要考查二项式定理的应用,在二项展开式中,通过给变量赋值,求得某些项的系数和,是一种简单有效的方法,属于基础题.
8.观察下列各式:13=12,13+23 ( http: / / www.21cnjy.com )=32,13+23+33=62,13+23+33+43=102,则得到的一般结论是 13+23+33+43+…+n3=[]2 .
【考点】归纳推理.
【专题】规律型.
【分析】根据题意,分析题干所给的等式 ( http: / / www.21cnjy.com )可得:13+23=(1+2)2=32,13+23+33=(1+2+3)2 =62,13+23+33+43=(1+2+3+4)2 =102,进而可得答案.
【解答】解:根据题意,分析题干所给的等式可得:
13+23=(1+2)2=32,
13+23+33=(1+2+3)2 =62,
13+23+33+43=(1+2+3+4)2 =102,
则13+23+33+43+…+n3=(1+2+3+4+…+n)2 =[]2,
故答案为:13+23+33+43+…+n3=[]2,
【点评】本题考查归纳推理,解题的关键是发现各个等式之间变化的规律以及每个等式左右两边的关系.
9.设(3+)n的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为 4 .
【考点】二项式定理的应用.
【专题】计算题;二项式定理.
【分析】利用赋值法及二项式系数和公式求出P、S,列出方程求得n.
【解答】解:由题意,4n+2n=272,
∴(2n﹣16)(2n+17)=0,
∴2n=16,
∴n=4.
故答案为:4.
【点评】本题考查赋值法求二项展开式系数和的方法;二项式系数和公式为2n,比较基础.
10.直线方程Ax+By=0,若从0, ( http: / / www.21cnjy.com )1,2,3,5,6这六个数字中每次取两个不同的数作为系数A、B的值,则方程Ax+By=0所表示的不同直线的条数是 18 .
【考点】直线的一般式方程.
【专题】直线与圆.
【分析】选中0时,Ax+By=0共能表达2条直线;当A、B从1,2,3,5,6五个数字中取值时,由排列组合的知识可得.
【解答】解:(1)当A或B中有一个取0时,另一个不论取何值,
方程都只能表示2条直线x=0和y=0.
即选中0时,Ax+By=0共能表示2条直线;
(2)当A、B从1,2,3,5,6五个数字中取值时,共有=5×4=20,
但当取值为(1,3)和(2,6)以及(3,1)和(6,2)时,
还有(1,2)和(3,6)及(2,1)和(6,3)时表示同一条直线,
∴当A、B从1,2,3,5,6五个数字中取值时,Ax+By=0共能表达20﹣4=16条直线.
综上所述,表示成不同直线的条数是2+16=18条
故答案为:18
【点评】本题考查直线的一般式方程,解题时要注意分类讨论思想和排列组合知识的合理运用,属基础题.
11.已知数列{an}(n∈N ( http: / / www.21cnjy.com )*)是首项为2,公比为3的等比数列,则a1C﹣a2C+a3C﹣a4C+a5C﹣a6C+a7C= 128 .
【考点】等比数列的性质.
【专题】等差数列与等比数列.
【分析】由等比数列的通项公式可得an,代入要求的式子由二项式定理可得.
【解答】解:∵数列{an}(n∈N*)是首项为2,公比为3的等比数列,
∴等比数列{an}的通项公式an=2×3n﹣1,
∴a1C﹣a2C+a3C﹣a4C+a5C﹣a6C+a7C
=2(30C﹣31C+32C﹣33C+34C﹣35C+36C)
=2(1﹣3)6=27=128
故答案为:128
【点评】本题考查等比数列的通项公式,涉及二项式定理,属中档题.
12.用数学归纳法证明结论:(n+1) ( http: / / www.21cnjy.com )(n+2)…(n+n)=2n×1×2×…×(2n﹣1)(n∈N*)时,从“k到k+1”左边需增乘的代数式为 2(2k+1) .
【考点】数学归纳法.
【专题】点列、递归数列与数学归纳法.
【分析】分别求出n=k时左端的表达式,和n=k+1时左端的表达式,比较可得“n从k到k+1”左端需增乘的代数式.
【解答】解:当n=k时,左边=(k+1)(k+2)…(k+k)=(k+1)(k+2)(k+3)…(2k),
当n=k+1时,左边=(k+1+1)(k+1+2)…(k+k)(k+1+k)(k+1+k+1),
故当“n从k到k+1”左端需增乘的代数式为=2(2k+1),
故答案为:2(2k+1).
【点评】本题考查用数学归纳法证明等式,分别求出n=k时左端的表达式和n=k+1时左端的表达式,是解题的关键.
13.如图是某市4月1日至14日的空气质量 ( http: / / www.21cnjy.com )指数趋势图,空气质量指数小于100表示空气质量优良,记5分,空气质量指数大于200表示空气重度污染记1分,空气质量指数在100和200之间(含100和200)表示中度污染,记3分.某调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分的可能抽样情况有 252 种.
【考点】计数原理的应用.
【专题】排列组合.
【分析】有图可知,5分的有7 ( http: / / www.21cnjy.com )天,1分的有2天,3分的有5天,调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分,因为5+5+1=11,5+5+3=13,5+3+3=11,5+5+5=15,故分四类,根据分类计数原理得以解决.
【解答】解:有图可知,空气质量指数小于 ( http: / / www.21cnjy.com )100表示空气质量优良,记5分,有7天,空气质量指数大于200表示空气重度污染记1分,有2天,空气质量指数在100和200之间(含100和200)表示中度污染,记3分,有5天,调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分,
因为5+5+1=11,5+5+3=13,5+3+3=11,5+5+5=15,
故分四类,第一类,得分为(5,5,1),有C72C21=42种,
第二类,得分为(5,5,3),有C72C51=105种,
第三类,得分为(5,3,3),有C71C52=70种,
第四类,得分为(5,5,5),有C73=35种,
根据分类计数原理,得共有42+105+70+35=252种,
故答案为:252.
【点评】本题考查了分类计数原理,关键是分类.
14.﹣2C+3C﹣4C+…+(﹣1)n(n+1)C= ﹣1 .
【考点】二项式定理的应用.
【专题】二项式定理.
【分析】根据 x (1﹣x)n=x(﹣ x+ x2+…+(﹣1)n xn),两边对x求导,再把x=1代入上式,可得要求式子的值.
【解答】解:∵要求﹣2C+3C﹣4C+…+(﹣1)n(n+1)C=,只要求出1﹣2C+3C﹣4C+…+(﹣1)n(n+1)C即可.
∵x (1﹣x)n=x(﹣ x+ x2+…+(﹣1)n xn),两边对x求导,可得
(1﹣x)n﹣x n(1﹣x)n﹣1=1﹣2C x+3C x2﹣4C x3+…+(﹣1)n(n+1)C xn,
再把x=1代入上式,可得0=1﹣2C+3C﹣4C+…+(﹣1)n(n+1)C,
∴2C+3C﹣4C+…+(﹣1)n(n+1)C=﹣1,
故答案为:﹣1.
【点评】本题主要考查二项式定理的应用,体现了转化的数学思想,属于中档题.
二、解答题(本大题共6小题,共计90分,解答时应写出文字说明、证明过程或演算步骤)
15.在复平面内,复数2﹣i,1+i,4所对应的点分别是A、B、C,四边形ABCD为平行四边形.
(1)求点D所对应的复数;
(2)求 ABCD的对角线BD的长.
【考点】复数代数形式的混合运算.
【专题】数系的扩充和复数.
【分析】(1)由题意知,在复平面内点A、 ( http: / / www.21cnjy.com )B、C 所对应的坐标分别为(2,﹣1),(1,1),(4,0),设点D的坐标为(x,y),由于四边形ABCD是平行四边形,可得,解出即可得出;
(2)在复平面内点B、D 所对应的坐标分别为(1,1)、(5,﹣2),利用两点之间的距离公式即可得出.
【解答】解:(1)由题意知,在复平面内点A、B、C 所对应的坐标分别为(2,﹣1),(1,1),(4,0),
设点D的坐标为(x,y),则=(﹣1,2),=(4﹣x,﹣y),
∵四边形ABCD是平行四边形,∴,即(﹣1,2)=(4﹣x,﹣y),
∴,解得.
∴点D所对应的复数为5﹣2i.
(2)∵在复平面内点B、D 所对应的坐标分别为(1,1)、(5,﹣2),
∴|BD|==5.
【点评】本题考查了复数的几何意义、向量的坐标运算、平行四边形的性质,考查了推理能力与计算能力,属于中档题.
16.已知:a,b,c,(a,b,c∈R)成等比数列,且公比q≠1,求证:1﹣a,1﹣b,1﹣c不可能成等比数列.
【考点】等比关系的确定.
【专题】等差数列与等比数列.
【分析】利用反证法结合等比数列的定义进行证明即可.
【解答】证明:假设1﹣a,1﹣b,1﹣c不成等比数列,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
则(1﹣b)2=(1﹣a)(1﹣c)①﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
∵a,b,c成等比数列,∴b2=ac,②﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
将②代入①,整理得2b=a+c﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
∴2aq=a+aq2,q2﹣2q+1=0,
从而q=1,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
这与已知q≠1矛盾,
∴1﹣a,1﹣b,1﹣c不可能成等比数列﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
【点评】本题主要考查等比数列等比关系的判断,利用反证法是解决本题的关键.
17.3名男生,4名女生排成一排,问:
(1)3名男生不相邻,有多少种排法?
(2)甲、乙、丙、丁四人必须站在一起,且甲在乙的左边(不一定相邻),有多少种排法?
(3)甲不在最左边,乙不在最右边,有多少排法?
【考点】排列、组合的实际应用.
【专题】计算题;排列组合.
【分析】(1)根据题意,用插空法分2步进行分 ( http: / / www.21cnjy.com )析:①、先将4名女生排好,排好后有5个空位,②、在5个空位中,任选3个,安排3名男生,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(2)根据题意,用捆绑法分析:①、将 ( http: / / www.21cnjy.com )甲、乙、丙、丁四人看成一个整体,计算可得四人之间的顺序,②、将这个整体与剩余的3个人进行全排列,可得其排法数目,由分步计数原理计算可得答案;
(3)根据题意,分2种情况讨论:①、若 ( http: / / www.21cnjy.com )甲在最右边,将剩余的6人全排列即可,②、若甲不在最右边,分别求出甲、乙以及剩余5人的排法数目,由分步计数原理可得其情况数目,综合2种情况,由分类计数原理计算可得答案.
【解答】解:(1)根据题意,分2步进行分析:
①、先将4名女生排好,有A44=24种情况,排好后有5个空位,
②、在5个空位中,任选3个,安排3名男生,有A53=60种情况,
则共有24×60=1440种排法,
∴3名男生不相邻有1440种排法;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(2)根据题意,分2步进行分析:
①、将甲、乙、丙、丁四人看成一个整体,
由于甲在乙的左边(不一定相邻),则四个人之间的顺序有A44=12种情况,
②、将这个整体与剩余的3个人进行全排列,有A44=24种排法,
则共有12×24=288种排法,
故甲、乙、丙、丁四人必须站在一起,且甲在乙的左边(不一定相邻)有288种排法;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(3)根据题意,分2种情况讨论:
①、若甲在最右边,有A66=720种排法,
②、若甲不在最右边,
甲在5个位置中选1个,有A51种情况,
乙也有5个位置可选,有A51种情况,
剩下的5个人进行全排列,有A55种情况,
此时一共有A51×A51×A55=3000种排法,
则共有720+3000=3720种排法,
∴甲不在最左边、乙不在最右边有3720种排法.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
【点评】本题考查排列组合的运用,需要牢记常见问题的处理方法,如不相邻问题用插空法,相邻问题用捆绑法.
18.已知在(﹣)n(n∈N*)的展开式中,第6项为常数项.
(1)求n的值及展开式中含x2的项的系数;
(2)①求展开式中所有有理项;
②求展开式中系数的绝对值最大的项.
【考点】二项式定理的应用;二项式系数的性质.
【专题】二项式定理.
【分析】(1)根据第六项为常数项,x的幂指数为零,求得n的值,在通项公式中,令x的幂指数为2,可得展开式中含x2的项的系数.
(2))①令x的幂指数为整数,求得自然数r的值,可得展开式中有理项.
②设展开式中第r+1项系数的绝对值最大,由(1)知,求得r的范围,可得整数r的值,从而得到展开式中系数的绝对值最大的项.
【解答】解:(1)由题意可得T6= =﹣ 为常数项,故有n﹣10=0,∴n=10.
故通项公式为 Tr+1= ,令=2,求得r=2,故展开式中含x2的项的系数为 =.
(2)①由(1)知为整数,且r=0,1,2,3,…10,故r=2,5,8,
∴展开式中有理项为 T3=x2,T6=﹣,T9=.
②设展开式中第r+1项系数的绝对值最大,由(1)知,
解得≤r≤,又r为整数,所以r=3,展开式中系数的绝对值最大的项为T4=﹣15.
【点评】本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于中档题.
19.设函数f(x)=ax2+bx+c(a,b,c∈R).
(1)若f(1)=0,a>b>c,求证:<a.
(2)若f(1)=﹣,3a>2c>2b,求证:
①a>0,且﹣3<<﹣;
②函数f(x)在区间(0,2)内至少有一个零点.
【考点】二次函数的性质.
【专题】函数的性质及应用.
【分析】(1)先求出c=﹣a﹣b,a>0,c<0,再利用分析法由结论入手进行证明即可;
(2)①先求出a>0,b<0,可得﹣3a<b<﹣a.从而证出结论;②先求出f(0),f(2),通过讨论c的正负,从而证出结论.
【解答】(1)证明:∵f(1)=a+b+c=0,a>b>c,
∴c=﹣a﹣b,a>0,c<0,
要证<a,只需证b2﹣ac<3a2,
只需证b2+a(a+b)<3a2,
只需证2a2﹣ab﹣b2>0,
只需证(a﹣b)(2a+b)>0,
只需证(a﹣b)(a﹣c)>0.
因为a>b>c,所以a﹣b>0,a﹣c>0,
所以(a﹣b)(a﹣c)>0显然成立.
故原不等式成立.
(2)证明:①f(1)=a+b+c=﹣,即3a+2b+2c=0.
又3a>2c>2b,所以3a>0,2b<0,则a>0,b<0.
又2c=﹣3a﹣2b,3a>2c>2b,
所以3a>﹣3a﹣2b>2b.可得﹣3a<b<﹣a.
因为a>0,所以﹣3<<﹣.
②f(0)=c,f(2)=4a+2b+c=a﹣c,
i)当c>0时,f(0)=c>0且f(1)=﹣<0,
所以函数f(x)在(0,1)内至少有一个零点.
ii)当c≤0时,f(1)=﹣<0且f(2)=a﹣c>0,
所以函数f(x)在(1,2)内至少有一个零点.
综上,f(x)在区间(0,2)内至少有一个零点.
【点评】本题考查了二次函数的性质,考查不等式的证明,是一道中档题.
20.已知数列{an}是等差数列,(1+)m(m∈N*)展开式的前三项的系数分别为a1,a2,a3.
(1)求(1+)m(m∈N*)的展开式中二项式系数最大的项;
(2)当n≥2(n∈N*)时,试猜测+++…+与的大小并证明.
【考点】用数学归纳法证明不等式;等差数列的性质;二项式系数的性质.
【专题】不等式的解法及应用.
【分析】(1)由二项式定理和等差数列可得m的值,由二项式系数可得;
(2)由(1)知an=3n﹣2,验证可得当n=2或3时, +++…+>,猜测结论并由数学归纳法证明即可.
【解答】解:(1)由二项式定理可得(1+)m=1+()+()2+…+()m,
由题意可得a1=1,a2=,a3=,
由数列{an}是等差数列可得2a2=a1+a3,解得m=8,或m=1(舍去)
∴展开式中第五项的二项式系数最大,
∴二项式系数最大的项为T5=()4=x4;
(2)由(1)知an=3n﹣2,
当n=2时, +++…+=++=++=>
当n=3时, +++…+=++…+=++…+>
猜测当n≥2时, +++…+>,下面由数学归纳法证明,
①由上述过程可知当n=2或3时,结论成立,
②假设n=k时,结论成立,即++…+>,
则当n=k+1时, ++…+
=(++…+)+(++…+﹣)
>+(++…+﹣)>+﹣
=+,
由k≥3可得3k2﹣7k﹣3>0,[3(k+1)2﹣2][3k﹣2]>0,
∴++…+>
综合①②可得,当n≥2时, +++…+>
【点评】本题考查不等式的证明,涉及数学归纳法和二项式定理以及等差数列的性质,属难题.
一、填空题(本大题共14小题,每小题5分,共计70分。不需要写出解答过程,请把答案直接填写在相应位置上)
1.若复数z=m(m+1)+(m+1)i(i为虚数单位)是纯虚数,则实数m的值为 .
2.“因为自然数是整数(大前提),而是自然数(小前提),所以是整数(结论)”,上面的推理是因为 (填“大前提”或“小前提”)错误导致结论错误.
3.有5本不同的书,从中选2本送给2名同学,每人各一本,共有 (填数字)种不同的送法.
4.设复数z满足i(z+1)=﹣3+2i(i为虚数单位),则z等于 .
5.有如下真命题:“若数列{an}是一个公 ( http: / / www.21cnjy.com )差为d的等差数列,则数列{an+an+1+an+2}是公差为3d的等差数列.”把上述命题类比到等比数列中,可得真命题是“ .”(注:填上你认为可以成为真命题的一种情形即可)
6.已知复数z满足|z+4﹣3i|=2(i为虚数单位).则|z|的最大值为 .
7.设(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n,那么a2+a4+…+a2n= .
8.观察下列各式:13=12,13+23=32,13+23+33=62,13+23+33+43=102,则得到的一般结论是 .
9.设(3+)n的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为 .
10.直线方程Ax+By=0,若从0,1, ( http: / / www.21cnjy.com )2,3,5,6这六个数字中每次取两个不同的数作为系数A、B的值,则方程Ax+By=0所表示的不同直线的条数是 .
11.已知数列{an}(n ( http: / / www.21cnjy.com )∈N*)是首项为2,公比为3的等比数列,则a1C﹣a2C+a3C﹣a4C+a5C﹣a6C+a7C= .
12.用数学归纳法证明结论:(n+1) ( http: / / www.21cnjy.com )(n+2)…(n+n)=2n×1×2×…×(2n﹣1)(n∈N*)时,从“k到k+1”左边需增乘的代数式为 .
13.如图是某市4月1日至14日的 ( http: / / www.21cnjy.com )空气质量指数趋势图,空气质量指数小于100表示空气质量优良,记5分,空气质量指数大于200表示空气重度污染记1分,空气质量指数在100和200之间(含100和200)表示中度污染,记3分.某调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分的可能抽样情况有 种.
14.﹣2C+3C﹣4C+…+(﹣1)n(n+1)C= .
二、解答题(本大题共6小题,共计90分,解答时应写出文字说明、证明过程或演算步骤)
15.在复平面内,复数2﹣i,1+i,4所对应的点分别是A、B、C,四边形ABCD为平行四边形.
(1)求点D所对应的复数;
(2)求 ABCD的对角线BD的长.
16.已知:a,b,c,(a,b,c∈R)成等比数列,且公比q≠1,求证:1﹣a,1﹣b,1﹣c不可能成等比数列.
17.3名男生,4名女生排成一排,问:
(1)3名男生不相邻,有多少种排法?
(2)甲、乙、丙、丁四人必须站在一起,且甲在乙的左边(不一定相邻),有多少种排法?
(3)甲不在最左边,乙不在最右边,有多少排法?
18.已知在(﹣)n(n∈N*)的展开式中,第6项为常数项.
(1)求n的值及展开式中含x2的项的系数;
(2)①求展开式中所有有理项;
②求展开式中系数的绝对值最大的项.
19.设函数f(x)=ax2+bx+c(a,b,c∈R).
(1)若f(1)=0,a>b>c,求证:<a.
(2)若f(1)=﹣,3a>2c>2b,求证:
①a>0,且﹣3<<﹣;
②函数f(x)在区间(0,2)内至少有一个零点.
20.已知数列{an}是等差数列,(1+)m(m∈N*)展开式的前三项的系数分别为a1,a2,a3.
(1)求(1+)m(m∈N*)的展开式中二项式系数最大的项;
(2)当n≥2(n∈N*)时,试猜测+++…+与的大小并证明.
2014-2015学年江苏省徐州市新沂市高二(下)期中数学试卷(理科)
参考答案与试题解析
一、填空题(本大题共14小题,每小题5分,共计70分。不需要写出解答过程,请把答案直接填写在相应位置上)
1.若复数z=m(m+1)+(m+1)i(i为虚数单位)是纯虚数,则实数m的值为 0 .
【考点】复数的基本概念.
【专题】数系的扩充和复数.
【分析】根据复数为纯虚数的概念,得到复数的实部为0,并且虚部不为0求出m.
【解答】解:因为复数z=m(m+1)+(m+1)i(i为虚数单位)是纯虚数,所以,解得m=0;
故答案为:0.
【点评】本题考查了复数的基本概念;如果复数a+bi(a,b是实数)是纯虚数,那么a=0并且b≠0.
2.“因为自然数是整数(大前提), ( http: / / www.21cnjy.com )而是自然数(小前提),所以是整数(结论)”,上面的推理是因为 小前提 (填“大前提”或“小前提”)错误导致结论错误.
【考点】演绎推理的意义.
【专题】推理和证明.
【分析】要分析一个演绎推理是否正确,主要观察 ( http: / / www.21cnjy.com )所给的大前提,小前提和结论及推理形式是否都正确,根据这几个方面都正确,才能得到这个演绎推理正确.
【解答】解:“因为自然数是整数(大前提),而是自然数(小前提),所以是整数(结论)”,
大前提是:自然数是整数,正确;
小前提是:是自然数,错误,
故导致结论错误的原因是小前提错误,
故答案为:小前提;
【点评】本题考查演绎推理,考查学生分析解决问题的能力,属于基础题
3.有5本不同的书,从中选2本送给2名同学,每人各一本,共有 20 (填数字)种不同的送法.
【考点】计数原理的应用.
【专题】排列组合.
【分析】根据题意,分析可得本题为排列问题,只需从5本不同的书中顺序选出2本,对应送给2位同学即可,由排列数公式计算可得答案
【解答】解:根据题意,只需从5本不同的书中顺序选出2本,对应送给2位同学即可,
有A52=20种方法;
故答案为:20.
【点评】本题考查排列的应用,解题时要首先要分析题意,明确是排列,还是组合问题.
4.设复数z满足i(z+1)=﹣3+2i(i为虚数单位),则z等于 1+3i .
【考点】复数相等的充要条件.
【分析】根据复数相等的条件,即可得到结论.
【解答】解:设z=a+bi,
则由i(z+1)=﹣3+2i得i(a+bi+1)=﹣3+2i=(a+1)i﹣b,
即,解得a=1,b=3,
故z=1+3i,
故答案为:1+3i
【点评】本题主要考查复数的求解,根据复数相等的条件,建立条件关系是解决本题的关键.
5.有如下真命题:“若数列 ( http: / / www.21cnjy.com ){an}是一个公差为d的等差数列,则数列{an+an+1+an+2}是公差为3d的等差数列.”把上述命题类比到等比数列中,可得真命题是“ 若数列{bn}是公比为q的等比数列,则数列{bn bn+1 bn+2}是公比为q3的等比数列;或填为:若数列{bn}是公比为q的等比数列,则数列{bn+bn+1+bn+2}是公比为q的等比数列 .”(注:填上你认为可以成为真命题的一种情形即可)
【考点】归纳推理.
【专题】开放型.
【分析】是一个类比推理的 ( http: / / www.21cnjy.com )问题,在类比推理中,等差数列到等比数列的类比推理方法一般为:加减运算类比推理为乘除运算,累加类比为累乘,由:“若数列{an}是一个公差为d的等差数列,则数列{an+an+1+an+2}是公差为3d的等差数列.”类比推理得:“若数列{bn}是公比为q的等比数列,则数列{bn bn+1 bn+2}是公比为q3的等比数列;或:若数列{bn}是公比为q的等比数列,则数列{bn+bn+1+bn+2}是公比为q的等比数列”
【解答】解:由等差数列的性质类比推理等比数列的性质时
类比推理方法一般为:
加减运算类比推理为乘除运算,
累加类比为累乘,
由:“若数列{an}是一个公差为d的等差数列,则数列{an+an+1+an+2}是公差为3d的等差数列.”
类比推理得:
“若数列{bn}是公比为q的等比数列,则数列{bn bn+1 bn+2}是公比为q3的等比数列;”
或“若数列{bn}是公比为q的等比数列,则数列{bn+bn+1+bn+2}是公比为q的等比数列”
故答案:若数列{bn}是公比为q的等比 ( http: / / www.21cnjy.com )数列,则数列{bn bn+1 bn+2}是公比为q3的等比数列;或填为:若数列{bn}是公比为q的等比数列,则数列{bn+bn+1+bn+2}是公比为q的等比数列.
【点评】类比推理的一般步骤是:(1)找 ( http: / / www.21cnjy.com )出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).
6.已知复数z满足|z+4﹣3i|=2(i为虚数单位).则|z|的最大值为 7 .
【考点】复数的代数表示法及其几何意义.
【分析】利用不等式|a|﹣|b|≤|a±b|≤|a|+|b|即可得出结论.
【解答】解:∵复数z满足|z+4﹣3i|=2(i为虚数单位),
∴|z+(4﹣3i)|=2,
∴|z|﹣|4﹣3i|≤|z+(4﹣3i)|=2,
∴|z|≤2+|4﹣3i|=2+5=7,
∴|z|的最大值为7.
故答案为:7.
【点评】本题考查了复数的代数运算与几何意义的应用问题,是基础题目.
7.设(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n,那么a2+a4+…+a2n= .
【考点】二项式系数的性质.
【专题】二项式定理.
【分析】在所给的等式中,令x=0求 ( http: / / www.21cnjy.com )得a0=1,再分别令x=1、x=﹣1,可得2个式子,再把这2个式子相加,变形即可求得a2+a4+…+a2n的值.
【解答】解:在(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n中,令x=0可得a0=1.
令x=1,可得 a0+a1+a2+a3+…+a2n﹣1+a2n=3n,
再令x=﹣1可得a0﹣a1+a2﹣a3+…﹣a2n﹣1+a2n=1,
再把这两个等式相加可得2(a0+a2+a4+…+a2n)=3n+1,
由此可得a2+a4+…+a2n=,
故答案为:.
【点评】本题主要考查二项式定理的应用,在二项展开式中,通过给变量赋值,求得某些项的系数和,是一种简单有效的方法,属于基础题.
8.观察下列各式:13=12,13+23 ( http: / / www.21cnjy.com )=32,13+23+33=62,13+23+33+43=102,则得到的一般结论是 13+23+33+43+…+n3=[]2 .
【考点】归纳推理.
【专题】规律型.
【分析】根据题意,分析题干所给的等式 ( http: / / www.21cnjy.com )可得:13+23=(1+2)2=32,13+23+33=(1+2+3)2 =62,13+23+33+43=(1+2+3+4)2 =102,进而可得答案.
【解答】解:根据题意,分析题干所给的等式可得:
13+23=(1+2)2=32,
13+23+33=(1+2+3)2 =62,
13+23+33+43=(1+2+3+4)2 =102,
则13+23+33+43+…+n3=(1+2+3+4+…+n)2 =[]2,
故答案为:13+23+33+43+…+n3=[]2,
【点评】本题考查归纳推理,解题的关键是发现各个等式之间变化的规律以及每个等式左右两边的关系.
9.设(3+)n的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为 4 .
【考点】二项式定理的应用.
【专题】计算题;二项式定理.
【分析】利用赋值法及二项式系数和公式求出P、S,列出方程求得n.
【解答】解:由题意,4n+2n=272,
∴(2n﹣16)(2n+17)=0,
∴2n=16,
∴n=4.
故答案为:4.
【点评】本题考查赋值法求二项展开式系数和的方法;二项式系数和公式为2n,比较基础.
10.直线方程Ax+By=0,若从0, ( http: / / www.21cnjy.com )1,2,3,5,6这六个数字中每次取两个不同的数作为系数A、B的值,则方程Ax+By=0所表示的不同直线的条数是 18 .
【考点】直线的一般式方程.
【专题】直线与圆.
【分析】选中0时,Ax+By=0共能表达2条直线;当A、B从1,2,3,5,6五个数字中取值时,由排列组合的知识可得.
【解答】解:(1)当A或B中有一个取0时,另一个不论取何值,
方程都只能表示2条直线x=0和y=0.
即选中0时,Ax+By=0共能表示2条直线;
(2)当A、B从1,2,3,5,6五个数字中取值时,共有=5×4=20,
但当取值为(1,3)和(2,6)以及(3,1)和(6,2)时,
还有(1,2)和(3,6)及(2,1)和(6,3)时表示同一条直线,
∴当A、B从1,2,3,5,6五个数字中取值时,Ax+By=0共能表达20﹣4=16条直线.
综上所述,表示成不同直线的条数是2+16=18条
故答案为:18
【点评】本题考查直线的一般式方程,解题时要注意分类讨论思想和排列组合知识的合理运用,属基础题.
11.已知数列{an}(n∈N ( http: / / www.21cnjy.com )*)是首项为2,公比为3的等比数列,则a1C﹣a2C+a3C﹣a4C+a5C﹣a6C+a7C= 128 .
【考点】等比数列的性质.
【专题】等差数列与等比数列.
【分析】由等比数列的通项公式可得an,代入要求的式子由二项式定理可得.
【解答】解:∵数列{an}(n∈N*)是首项为2,公比为3的等比数列,
∴等比数列{an}的通项公式an=2×3n﹣1,
∴a1C﹣a2C+a3C﹣a4C+a5C﹣a6C+a7C
=2(30C﹣31C+32C﹣33C+34C﹣35C+36C)
=2(1﹣3)6=27=128
故答案为:128
【点评】本题考查等比数列的通项公式,涉及二项式定理,属中档题.
12.用数学归纳法证明结论:(n+1) ( http: / / www.21cnjy.com )(n+2)…(n+n)=2n×1×2×…×(2n﹣1)(n∈N*)时,从“k到k+1”左边需增乘的代数式为 2(2k+1) .
【考点】数学归纳法.
【专题】点列、递归数列与数学归纳法.
【分析】分别求出n=k时左端的表达式,和n=k+1时左端的表达式,比较可得“n从k到k+1”左端需增乘的代数式.
【解答】解:当n=k时,左边=(k+1)(k+2)…(k+k)=(k+1)(k+2)(k+3)…(2k),
当n=k+1时,左边=(k+1+1)(k+1+2)…(k+k)(k+1+k)(k+1+k+1),
故当“n从k到k+1”左端需增乘的代数式为=2(2k+1),
故答案为:2(2k+1).
【点评】本题考查用数学归纳法证明等式,分别求出n=k时左端的表达式和n=k+1时左端的表达式,是解题的关键.
13.如图是某市4月1日至14日的空气质量 ( http: / / www.21cnjy.com )指数趋势图,空气质量指数小于100表示空气质量优良,记5分,空气质量指数大于200表示空气重度污染记1分,空气质量指数在100和200之间(含100和200)表示中度污染,记3分.某调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分的可能抽样情况有 252 种.
【考点】计数原理的应用.
【专题】排列组合.
【分析】有图可知,5分的有7 ( http: / / www.21cnjy.com )天,1分的有2天,3分的有5天,调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分,因为5+5+1=11,5+5+3=13,5+3+3=11,5+5+5=15,故分四类,根据分类计数原理得以解决.
【解答】解:有图可知,空气质量指数小于 ( http: / / www.21cnjy.com )100表示空气质量优良,记5分,有7天,空气质量指数大于200表示空气重度污染记1分,有2天,空气质量指数在100和200之间(含100和200)表示中度污染,记3分,有5天,调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分,
因为5+5+1=11,5+5+3=13,5+3+3=11,5+5+5=15,
故分四类,第一类,得分为(5,5,1),有C72C21=42种,
第二类,得分为(5,5,3),有C72C51=105种,
第三类,得分为(5,3,3),有C71C52=70种,
第四类,得分为(5,5,5),有C73=35种,
根据分类计数原理,得共有42+105+70+35=252种,
故答案为:252.
【点评】本题考查了分类计数原理,关键是分类.
14.﹣2C+3C﹣4C+…+(﹣1)n(n+1)C= ﹣1 .
【考点】二项式定理的应用.
【专题】二项式定理.
【分析】根据 x (1﹣x)n=x(﹣ x+ x2+…+(﹣1)n xn),两边对x求导,再把x=1代入上式,可得要求式子的值.
【解答】解:∵要求﹣2C+3C﹣4C+…+(﹣1)n(n+1)C=,只要求出1﹣2C+3C﹣4C+…+(﹣1)n(n+1)C即可.
∵x (1﹣x)n=x(﹣ x+ x2+…+(﹣1)n xn),两边对x求导,可得
(1﹣x)n﹣x n(1﹣x)n﹣1=1﹣2C x+3C x2﹣4C x3+…+(﹣1)n(n+1)C xn,
再把x=1代入上式,可得0=1﹣2C+3C﹣4C+…+(﹣1)n(n+1)C,
∴2C+3C﹣4C+…+(﹣1)n(n+1)C=﹣1,
故答案为:﹣1.
【点评】本题主要考查二项式定理的应用,体现了转化的数学思想,属于中档题.
二、解答题(本大题共6小题,共计90分,解答时应写出文字说明、证明过程或演算步骤)
15.在复平面内,复数2﹣i,1+i,4所对应的点分别是A、B、C,四边形ABCD为平行四边形.
(1)求点D所对应的复数;
(2)求 ABCD的对角线BD的长.
【考点】复数代数形式的混合运算.
【专题】数系的扩充和复数.
【分析】(1)由题意知,在复平面内点A、 ( http: / / www.21cnjy.com )B、C 所对应的坐标分别为(2,﹣1),(1,1),(4,0),设点D的坐标为(x,y),由于四边形ABCD是平行四边形,可得,解出即可得出;
(2)在复平面内点B、D 所对应的坐标分别为(1,1)、(5,﹣2),利用两点之间的距离公式即可得出.
【解答】解:(1)由题意知,在复平面内点A、B、C 所对应的坐标分别为(2,﹣1),(1,1),(4,0),
设点D的坐标为(x,y),则=(﹣1,2),=(4﹣x,﹣y),
∵四边形ABCD是平行四边形,∴,即(﹣1,2)=(4﹣x,﹣y),
∴,解得.
∴点D所对应的复数为5﹣2i.
(2)∵在复平面内点B、D 所对应的坐标分别为(1,1)、(5,﹣2),
∴|BD|==5.
【点评】本题考查了复数的几何意义、向量的坐标运算、平行四边形的性质,考查了推理能力与计算能力,属于中档题.
16.已知:a,b,c,(a,b,c∈R)成等比数列,且公比q≠1,求证:1﹣a,1﹣b,1﹣c不可能成等比数列.
【考点】等比关系的确定.
【专题】等差数列与等比数列.
【分析】利用反证法结合等比数列的定义进行证明即可.
【解答】证明:假设1﹣a,1﹣b,1﹣c不成等比数列,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
则(1﹣b)2=(1﹣a)(1﹣c)①﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
∵a,b,c成等比数列,∴b2=ac,②﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
将②代入①,整理得2b=a+c﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
∴2aq=a+aq2,q2﹣2q+1=0,
从而q=1,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
这与已知q≠1矛盾,
∴1﹣a,1﹣b,1﹣c不可能成等比数列﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
【点评】本题主要考查等比数列等比关系的判断,利用反证法是解决本题的关键.
17.3名男生,4名女生排成一排,问:
(1)3名男生不相邻,有多少种排法?
(2)甲、乙、丙、丁四人必须站在一起,且甲在乙的左边(不一定相邻),有多少种排法?
(3)甲不在最左边,乙不在最右边,有多少排法?
【考点】排列、组合的实际应用.
【专题】计算题;排列组合.
【分析】(1)根据题意,用插空法分2步进行分 ( http: / / www.21cnjy.com )析:①、先将4名女生排好,排好后有5个空位,②、在5个空位中,任选3个,安排3名男生,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(2)根据题意,用捆绑法分析:①、将 ( http: / / www.21cnjy.com )甲、乙、丙、丁四人看成一个整体,计算可得四人之间的顺序,②、将这个整体与剩余的3个人进行全排列,可得其排法数目,由分步计数原理计算可得答案;
(3)根据题意,分2种情况讨论:①、若 ( http: / / www.21cnjy.com )甲在最右边,将剩余的6人全排列即可,②、若甲不在最右边,分别求出甲、乙以及剩余5人的排法数目,由分步计数原理可得其情况数目,综合2种情况,由分类计数原理计算可得答案.
【解答】解:(1)根据题意,分2步进行分析:
①、先将4名女生排好,有A44=24种情况,排好后有5个空位,
②、在5个空位中,任选3个,安排3名男生,有A53=60种情况,
则共有24×60=1440种排法,
∴3名男生不相邻有1440种排法;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(2)根据题意,分2步进行分析:
①、将甲、乙、丙、丁四人看成一个整体,
由于甲在乙的左边(不一定相邻),则四个人之间的顺序有A44=12种情况,
②、将这个整体与剩余的3个人进行全排列,有A44=24种排法,
则共有12×24=288种排法,
故甲、乙、丙、丁四人必须站在一起,且甲在乙的左边(不一定相邻)有288种排法;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(3)根据题意,分2种情况讨论:
①、若甲在最右边,有A66=720种排法,
②、若甲不在最右边,
甲在5个位置中选1个,有A51种情况,
乙也有5个位置可选,有A51种情况,
剩下的5个人进行全排列,有A55种情况,
此时一共有A51×A51×A55=3000种排法,
则共有720+3000=3720种排法,
∴甲不在最左边、乙不在最右边有3720种排法.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
【点评】本题考查排列组合的运用,需要牢记常见问题的处理方法,如不相邻问题用插空法,相邻问题用捆绑法.
18.已知在(﹣)n(n∈N*)的展开式中,第6项为常数项.
(1)求n的值及展开式中含x2的项的系数;
(2)①求展开式中所有有理项;
②求展开式中系数的绝对值最大的项.
【考点】二项式定理的应用;二项式系数的性质.
【专题】二项式定理.
【分析】(1)根据第六项为常数项,x的幂指数为零,求得n的值,在通项公式中,令x的幂指数为2,可得展开式中含x2的项的系数.
(2))①令x的幂指数为整数,求得自然数r的值,可得展开式中有理项.
②设展开式中第r+1项系数的绝对值最大,由(1)知,求得r的范围,可得整数r的值,从而得到展开式中系数的绝对值最大的项.
【解答】解:(1)由题意可得T6= =﹣ 为常数项,故有n﹣10=0,∴n=10.
故通项公式为 Tr+1= ,令=2,求得r=2,故展开式中含x2的项的系数为 =.
(2)①由(1)知为整数,且r=0,1,2,3,…10,故r=2,5,8,
∴展开式中有理项为 T3=x2,T6=﹣,T9=.
②设展开式中第r+1项系数的绝对值最大,由(1)知,
解得≤r≤,又r为整数,所以r=3,展开式中系数的绝对值最大的项为T4=﹣15.
【点评】本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于中档题.
19.设函数f(x)=ax2+bx+c(a,b,c∈R).
(1)若f(1)=0,a>b>c,求证:<a.
(2)若f(1)=﹣,3a>2c>2b,求证:
①a>0,且﹣3<<﹣;
②函数f(x)在区间(0,2)内至少有一个零点.
【考点】二次函数的性质.
【专题】函数的性质及应用.
【分析】(1)先求出c=﹣a﹣b,a>0,c<0,再利用分析法由结论入手进行证明即可;
(2)①先求出a>0,b<0,可得﹣3a<b<﹣a.从而证出结论;②先求出f(0),f(2),通过讨论c的正负,从而证出结论.
【解答】(1)证明:∵f(1)=a+b+c=0,a>b>c,
∴c=﹣a﹣b,a>0,c<0,
要证<a,只需证b2﹣ac<3a2,
只需证b2+a(a+b)<3a2,
只需证2a2﹣ab﹣b2>0,
只需证(a﹣b)(2a+b)>0,
只需证(a﹣b)(a﹣c)>0.
因为a>b>c,所以a﹣b>0,a﹣c>0,
所以(a﹣b)(a﹣c)>0显然成立.
故原不等式成立.
(2)证明:①f(1)=a+b+c=﹣,即3a+2b+2c=0.
又3a>2c>2b,所以3a>0,2b<0,则a>0,b<0.
又2c=﹣3a﹣2b,3a>2c>2b,
所以3a>﹣3a﹣2b>2b.可得﹣3a<b<﹣a.
因为a>0,所以﹣3<<﹣.
②f(0)=c,f(2)=4a+2b+c=a﹣c,
i)当c>0时,f(0)=c>0且f(1)=﹣<0,
所以函数f(x)在(0,1)内至少有一个零点.
ii)当c≤0时,f(1)=﹣<0且f(2)=a﹣c>0,
所以函数f(x)在(1,2)内至少有一个零点.
综上,f(x)在区间(0,2)内至少有一个零点.
【点评】本题考查了二次函数的性质,考查不等式的证明,是一道中档题.
20.已知数列{an}是等差数列,(1+)m(m∈N*)展开式的前三项的系数分别为a1,a2,a3.
(1)求(1+)m(m∈N*)的展开式中二项式系数最大的项;
(2)当n≥2(n∈N*)时,试猜测+++…+与的大小并证明.
【考点】用数学归纳法证明不等式;等差数列的性质;二项式系数的性质.
【专题】不等式的解法及应用.
【分析】(1)由二项式定理和等差数列可得m的值,由二项式系数可得;
(2)由(1)知an=3n﹣2,验证可得当n=2或3时, +++…+>,猜测结论并由数学归纳法证明即可.
【解答】解:(1)由二项式定理可得(1+)m=1+()+()2+…+()m,
由题意可得a1=1,a2=,a3=,
由数列{an}是等差数列可得2a2=a1+a3,解得m=8,或m=1(舍去)
∴展开式中第五项的二项式系数最大,
∴二项式系数最大的项为T5=()4=x4;
(2)由(1)知an=3n﹣2,
当n=2时, +++…+=++=++=>
当n=3时, +++…+=++…+=++…+>
猜测当n≥2时, +++…+>,下面由数学归纳法证明,
①由上述过程可知当n=2或3时,结论成立,
②假设n=k时,结论成立,即++…+>,
则当n=k+1时, ++…+
=(++…+)+(++…+﹣)
>+(++…+﹣)>+﹣
=+,
由k≥3可得3k2﹣7k﹣3>0,[3(k+1)2﹣2][3k﹣2]>0,
∴++…+>
综合①②可得,当n≥2时, +++…+>
【点评】本题考查不等式的证明,涉及数学归纳法和二项式定理以及等差数列的性质,属难题.
同课章节目录
