13.3.1等腰三角形 课件(共21张PPT)
文档属性
| 名称 | 13.3.1等腰三角形 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-12 14:53:26 | ||
图片预览





文档简介
(共21张PPT)
人教版 八年级数学上
13.3.1等腰三角形的判定
学习目标
1.掌握等腰三角形的判定方法.(重点)
2.能够灵活运用等腰三角形的判定定理解决相关问题.(难点)
温故知新
想一想:等腰三角形都有哪些性质呢?
性质2:等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合.
(简写成“三线合一”)
性质1:等腰三角形的两个底角相等;
(简写成“等边对等角”)
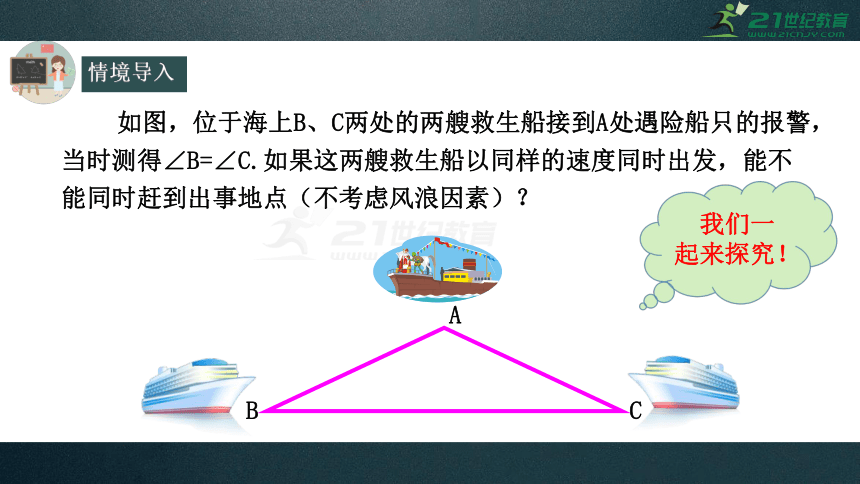
情境导入
A
B
C
如图,位于海上B、C两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
我们一起来探究!
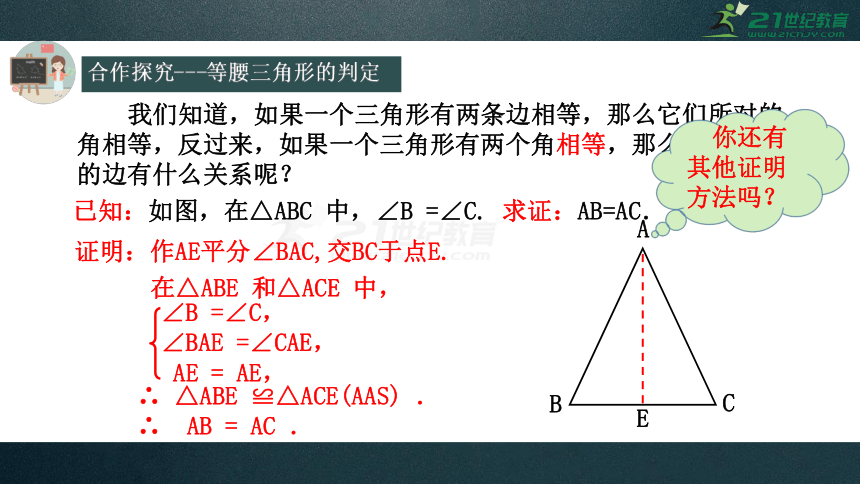
合作探究---等腰三角形的判定
我们知道,如果一个三角形有两条边相等,那么它们所对的
角相等,反过来,如果一个三角形有两个角相等,那么它们所对
的边有什么关系呢?
证明:作AE平分∠BAC,交BC于点E.
在△ABE 和△ACE 中,
E
∠B =∠C,
∠BAE =∠CAE,
AE = AE,
∴ △ABE ≌△ACE(AAS) .
∴ AB = AC .
已知:如图,在△ABC 中,∠B =∠C. 求证:AB=AC.
A
B
C
你还有其他证明方法吗?
这又是一个判定两条线段相等的根据之一.
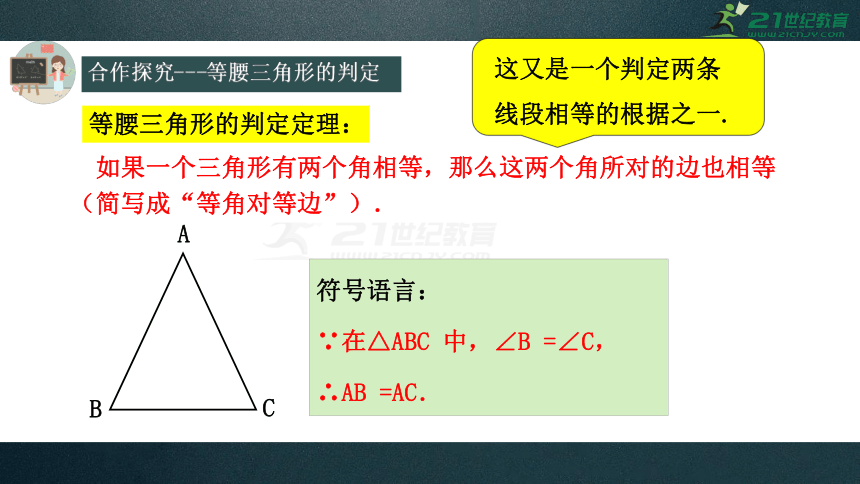
合作探究---等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等
(简写成“等角对等边”).
A
B
C
符号语言:
∵在△ABC 中,∠B =∠C,
∴AB =AC.
等腰三角形的判定定理:
典例精析
例1.求证:如果三角形一个外角的平分线平行于三角形的一边,
那么这个三角形是等腰三角形.
已知:∠CAE 是△ABC 的外角,∠1 =∠2,AD∥BC.
求证:AB =AC.
∠2 =∠C
证明:∵AD∥BC ,
∴∠1 =∠B
(两直线平行,内错角相等)
(两直线平行,同位角相等)
∵∠1 =∠2,
∴∠B =∠C.
∴AB =AC
(等边对等角)
典例精析
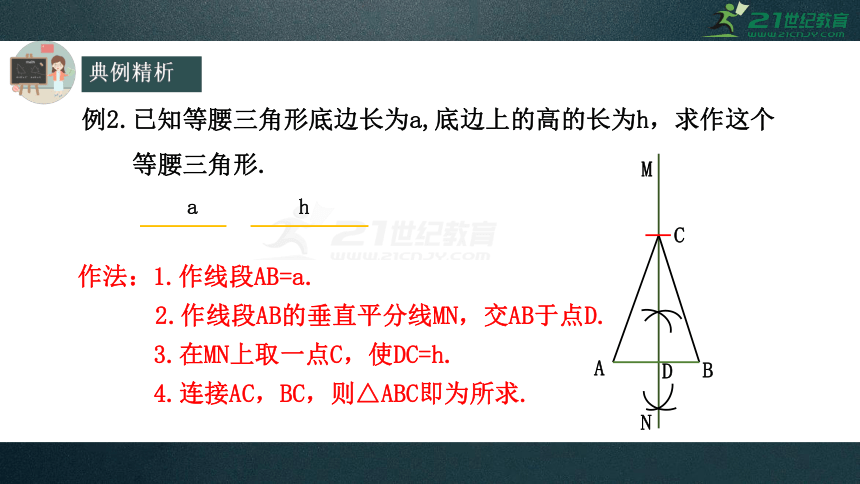
例2.已知等腰三角形底边长为a,底边上的高的长为h,求作这个
等腰三角形.
a
h
作法:1.作线段AB=a.
2.作线段AB的垂直平分线MN,交AB于点D.
3.在MN上取一点C,使DC=h.
4.连接AC,BC,则△ABC即为所求.
A
B
C
M
N
D
小试牛刀
2.如图,在△ABC中,∠A=36°,∠C=72°,BD是
△ABC的角平分线.若在边AB上截取BE=BC,连
接DE,则图中等腰三角形共有 。
5个
1.在△ABC中,其两个内角如下,能判定是等腰三角形的是( )
A.∠A=50°∠B=70° B.∠A=60°∠B=55°
C.∠A=100°∠B=30° D.∠A=75°∠B=30°
D
小试牛刀
3.如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
解:是
由折叠可知,∠EBD=∠CBD.
∵AD∥BC,∴∠EDB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE,△EBD是等腰三角形.
方法总结:平分角+平行=等腰三角形
E
小试牛刀
4.求证:如果三角形的一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
已知:如图,BD是△ABC的中线,AC=2BD.
求证:△ABC是直角三角形
证明:∵BD是△ABC的中线,
∴2AD=2CD=AC.
∵AC=2BD,
∴AD=BD,BD=CD
A
C
B
D
小试牛刀
4.求证:如果三角形的一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
∴∠DAB=∠DBA,∠DBC=∠DCB.
由三角形内角和知: ∠DAB+∠DBA+∠DBC+∠DCB=180°
∴2∠DBA+2∠DBC=180°
∴∠DBA+∠DBC=90°
∴ △ABC是直角三角形
A
C
B
D
小试牛刀
5.如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD.
解:∵ AB∥DC
∴∠A=∠C,∠B=∠D.
∵OA=OB
∴∠A=∠B
∴∠C=∠D
∴OC=OD
C
A
B
D
O
实战演练
1.如图,一艘轮船位于灯塔0的南偏东70°方向的A处,它以每小时45海里的速度向北方向航行,2小时后到达位于灯塔0的北偏东40°的B处,则B到灯塔0的距离为( )
A.45海里 B.90海里
C.80海里 D.67.5海里
B
O
B
A
40°
70°
北
东
实战演练
2.如图,在△ABC中,BC=15cm,BO,CO分别是∠ABC和∠ACB的平分线,且OD∥AB,OE∥AC,
则△PDE的周长是 cm。
15
C
B
A
O
E
D
实战演练
3.如图,已知点A、B的坐标分别为(1,0)
和(0,2),在坐标轴上找一点C,使△ABC
是等腰三角形,则符号条件的点C的坐标有
个。
8
O
y
x
B
A
综合演练
4.如图,AD是△ABC的角平分线,BE⊥AD交AD的延长线于
点E,EF∥AC交AB于点F. 求证:AF=FB.
证明:∵AD平分∠BAC, ∴∠BAE=∠EAC,
∵EF∥AC, ∴∠FEA=∠EAC,
∴∠FEA=∠DAF,∴AF=FE.
∵BE⊥AE,
∴∠FEA+∠BEF=90°,∠BAE+∠FBE=90°,
∴∠FBE=∠BEF,∴BF=EF,∴AF=BF.
能力提升
5.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
证明:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的平分线,∴∠BAE=∠EAC,
∴∠B+∠BAE=∠ACD+∠EAC,即∠CEF=∠CFE,
∴CE=CF,∴△CEF是等腰三角形.
课后作业
教材81页习题13.3第5、6、10题.
课堂小结
今天我们收获了哪些知识?
(畅所欲言)
1、如何判断一个三角形是等腰三角形?
2、你能说说我们现在学习了哪些判断两条线段相等的方法了?
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
13.3.1等腰三角形的判定
学习目标
1.掌握等腰三角形的判定方法.(重点)
2.能够灵活运用等腰三角形的判定定理解决相关问题.(难点)
温故知新
想一想:等腰三角形都有哪些性质呢?
性质2:等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合.
(简写成“三线合一”)
性质1:等腰三角形的两个底角相等;
(简写成“等边对等角”)
情境导入
A
B
C
如图,位于海上B、C两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
我们一起来探究!
合作探究---等腰三角形的判定
我们知道,如果一个三角形有两条边相等,那么它们所对的
角相等,反过来,如果一个三角形有两个角相等,那么它们所对
的边有什么关系呢?
证明:作AE平分∠BAC,交BC于点E.
在△ABE 和△ACE 中,
E
∠B =∠C,
∠BAE =∠CAE,
AE = AE,
∴ △ABE ≌△ACE(AAS) .
∴ AB = AC .
已知:如图,在△ABC 中,∠B =∠C. 求证:AB=AC.
A
B
C
你还有其他证明方法吗?
这又是一个判定两条线段相等的根据之一.
合作探究---等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等
(简写成“等角对等边”).
A
B
C
符号语言:
∵在△ABC 中,∠B =∠C,
∴AB =AC.
等腰三角形的判定定理:
典例精析
例1.求证:如果三角形一个外角的平分线平行于三角形的一边,
那么这个三角形是等腰三角形.
已知:∠CAE 是△ABC 的外角,∠1 =∠2,AD∥BC.
求证:AB =AC.
∠2 =∠C
证明:∵AD∥BC ,
∴∠1 =∠B
(两直线平行,内错角相等)
(两直线平行,同位角相等)
∵∠1 =∠2,
∴∠B =∠C.
∴AB =AC
(等边对等角)
典例精析
例2.已知等腰三角形底边长为a,底边上的高的长为h,求作这个
等腰三角形.
a
h
作法:1.作线段AB=a.
2.作线段AB的垂直平分线MN,交AB于点D.
3.在MN上取一点C,使DC=h.
4.连接AC,BC,则△ABC即为所求.
A
B
C
M
N
D
小试牛刀
2.如图,在△ABC中,∠A=36°,∠C=72°,BD是
△ABC的角平分线.若在边AB上截取BE=BC,连
接DE,则图中等腰三角形共有 。
5个
1.在△ABC中,其两个内角如下,能判定是等腰三角形的是( )
A.∠A=50°∠B=70° B.∠A=60°∠B=55°
C.∠A=100°∠B=30° D.∠A=75°∠B=30°
D
小试牛刀
3.如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
解:是
由折叠可知,∠EBD=∠CBD.
∵AD∥BC,∴∠EDB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE,△EBD是等腰三角形.
方法总结:平分角+平行=等腰三角形
E
小试牛刀
4.求证:如果三角形的一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
已知:如图,BD是△ABC的中线,AC=2BD.
求证:△ABC是直角三角形
证明:∵BD是△ABC的中线,
∴2AD=2CD=AC.
∵AC=2BD,
∴AD=BD,BD=CD
A
C
B
D
小试牛刀
4.求证:如果三角形的一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
∴∠DAB=∠DBA,∠DBC=∠DCB.
由三角形内角和知: ∠DAB+∠DBA+∠DBC+∠DCB=180°
∴2∠DBA+2∠DBC=180°
∴∠DBA+∠DBC=90°
∴ △ABC是直角三角形
A
C
B
D
小试牛刀
5.如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD.
解:∵ AB∥DC
∴∠A=∠C,∠B=∠D.
∵OA=OB
∴∠A=∠B
∴∠C=∠D
∴OC=OD
C
A
B
D
O
实战演练
1.如图,一艘轮船位于灯塔0的南偏东70°方向的A处,它以每小时45海里的速度向北方向航行,2小时后到达位于灯塔0的北偏东40°的B处,则B到灯塔0的距离为( )
A.45海里 B.90海里
C.80海里 D.67.5海里
B
O
B
A
40°
70°
北
东
实战演练
2.如图,在△ABC中,BC=15cm,BO,CO分别是∠ABC和∠ACB的平分线,且OD∥AB,OE∥AC,
则△PDE的周长是 cm。
15
C
B
A
O
E
D
实战演练
3.如图,已知点A、B的坐标分别为(1,0)
和(0,2),在坐标轴上找一点C,使△ABC
是等腰三角形,则符号条件的点C的坐标有
个。
8
O
y
x
B
A
综合演练
4.如图,AD是△ABC的角平分线,BE⊥AD交AD的延长线于
点E,EF∥AC交AB于点F. 求证:AF=FB.
证明:∵AD平分∠BAC, ∴∠BAE=∠EAC,
∵EF∥AC, ∴∠FEA=∠EAC,
∴∠FEA=∠DAF,∴AF=FE.
∵BE⊥AE,
∴∠FEA+∠BEF=90°,∠BAE+∠FBE=90°,
∴∠FBE=∠BEF,∴BF=EF,∴AF=BF.
能力提升
5.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
证明:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的平分线,∴∠BAE=∠EAC,
∴∠B+∠BAE=∠ACD+∠EAC,即∠CEF=∠CFE,
∴CE=CF,∴△CEF是等腰三角形.
课后作业
教材81页习题13.3第5、6、10题.
课堂小结
今天我们收获了哪些知识?
(畅所欲言)
1、如何判断一个三角形是等腰三角形?
2、你能说说我们现在学习了哪些判断两条线段相等的方法了?
https://www.21cnjy.com/help/help_extract.php
