1.4.2 用空间向量研究距离、夹角问题-第2课时课件(共52张PPT)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.4.2 用空间向量研究距离、夹角问题-第2课时课件(共52张PPT)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 11:34:26 | ||
图片预览









文档简介
(共52张PPT)
1.4 空间向量的应用
1.4.2 用空间向量研究距离、夹角问题
第2课时 用空间向量研究夹角问题
【学习目标】
1.知道两个相交平面夹角的含义,借助直线的方向向量和平面的法向量,
能求直线与直线、直线与平面所成的角,平面与平面的夹角.
2.能分析和解决一些立体几何中的角度问题,体会向量方法与综合几何方
法的共性和差异,体会直线的方向向量和平面的法向量的作用,感悟向量是研
究几何问题的有效工具.
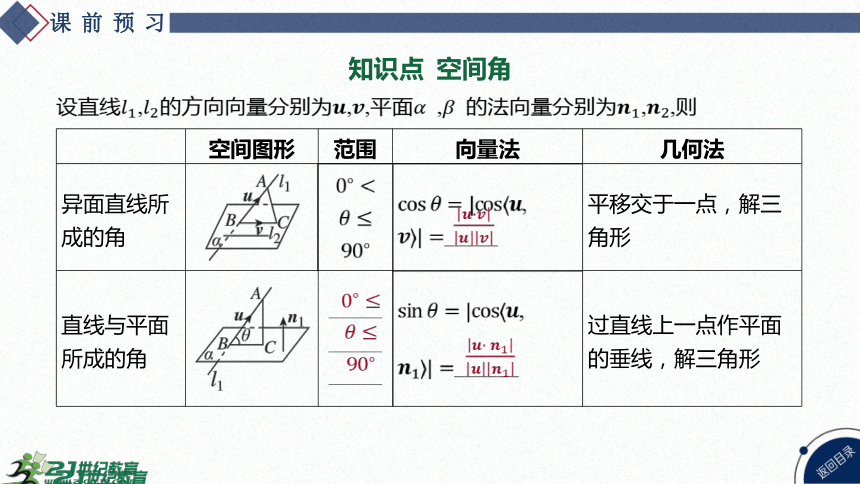
知识点 空间角
设直线,的方向向量分别为,,平面 , 的法向量分别为, ,则
空间图形 范围 向量法 几何法
异面直线所 成的角 , _____ 平移交于一点,解三
角形
直线与平面 所成的角 _____ _____ _____ , _ _____ 过直线上一点作平面
的垂线,解三角形
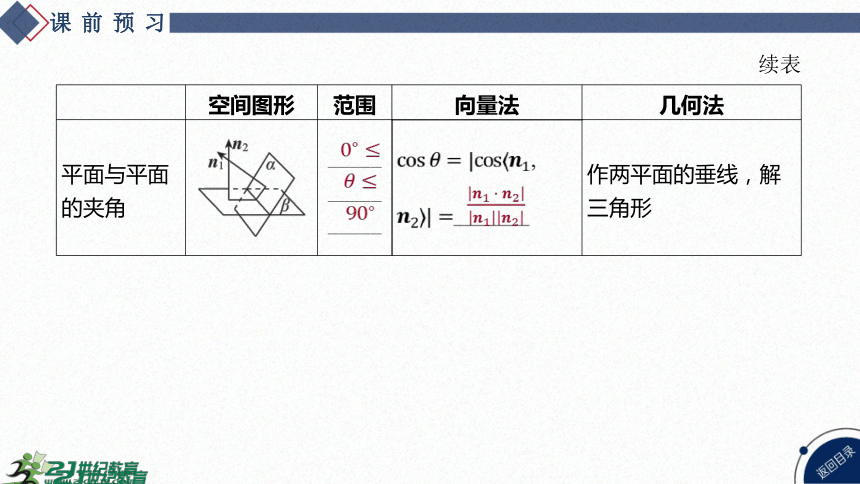
空间图形 范围 向量法 几何法
平面与平面 的夹角 _____ _____ _____ , _ ______ 作两平面的垂线,解
三角形
续表
【诊断分析】 判断正误.(请在括号中打“√”或“×”)
(1)异面直线所成的角与其方向向量的夹角相等.( )
×
[解析] 当两个方向向量的夹角是锐角或直角时,向量的夹角与异面直线所成的角相
等;当两个方向向量的夹角为钝角时,向量的夹角与异面直线所成的角互补.故错误.
(2)若平面 的法向量为,直线的方向向量为,直线与平面 所成的角为 ,
则 .( )
×
[解析] ,故错误.
(3)二面角的大小等于平面与平面的夹角.( )
×
[解析] 二面角中不大于 的二面角称为平面与平面的夹角.故错误.
探究点一 异面直线所成角的求法
例1 如图所示,在三棱柱中, 是
正三角形,点在平面上的射影为的中点 ,侧
面是边长为2的菱形,求异面直线与 所成
角的余弦值.
解:如图,连接,,因为点在平面上的射影为的中点 ,
所以 平面,又 平面, 平面,所以 ,
.
因为是正三角形,是的中点,所以 .
以 为原点建立如图所示的空间直角坐标系,则
,,, ,所以
, .
设异面直线与所成的角为 ,
则,即异面直线 与
所成角的余弦值为 .
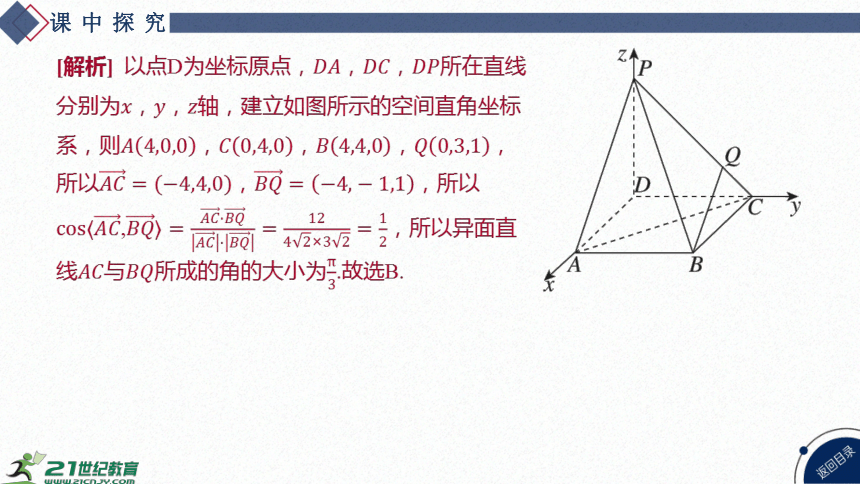
变式 [2024·重庆巴渝学校高二期中] 如图,在四棱锥
中, 底面,底面 为正方
形,,为上一点,且 ,则异
面直线与 所成的角的大小为( )
B
A. B. C. D.
[解析] 以点D为坐标原点,,, 所在直线
分别为,, 轴,建立如图所示的空间直角坐标
系,则,,, ,
所以, ,所以
, ,所以异面直
线与所成的角的大小为 .故选B.
[素养小结]
用向量法求异面直线所成的角时,常在两异面直线与上分别取点,和 ,
,则与分别为直线,的方向向量,若异面直线,所成的角为 ,则
.
运用向量法常有两种途径:
①基底法:在一些不适合建立空间直角坐标系的题型中,经常采用取基底的方法.
在由公式,求向量,的夹角时,关键是求出,与 ,
一般是把, 用基向量表示出来,再求有关的量.
②坐标法:根据题目条件建立恰当的空间直角坐标系,写出相关各点的坐标,利
用坐标法求异面直线所成的角,避免了传统找角或作角的步骤,使过程变得简
单.
探究点二 求直线和平面所成的角
例2 [2024·浙江浙南名校联盟高二期中] 已知三棱
柱满足 ,
, ,顶点 在平面
上的射影为点 .
(1)证明: 平面 ;
解:证明:由已知得 平面,又 平面,所以 ,
因为 ,所以,又因为 ,
, 平面,所以 平面 .
(2)若点为的中点,点为的中点,求直线与平面 所成角的
正弦值.
解:因为 平面, 平面,所以.在
中, ,所以 ,故 .
如图,以为原点,,所在直线分别为轴, 轴,过点
且与平行的直线为 轴,建立空间直角坐标系,
则,, ,
, ,
所以, .
设平面的法向量为 ,
则即
令,得,,所以平面的一个法向量为 .
设直线与平面所成的角为 ,
又,则 ,所以直线
与平面所成角的正弦值为 .
变式 如图,在四棱锥 中,
, , ,底面
是菱形,是的中点, .
(1)证明:平面 平面 ;
解:证明:如图,连接 ,
底面 是菱形,
且 , 是等边三角形,
又是的中点, .
, .
,, 平面, 平面 ,
又 平面, 平面 平面 .
(2)求直线与平面 所成角的正弦值.
解:, ,, .
底面是菱形,是的中点, ,
,又,,即 .
由(1)知,,, 以为原点,,,
所在直线分别为,, 轴,建立空间直角坐标系,如图,
则,,, ,
,,. 设 是平面
的法向量,
则取,得 .
设直线与平面所成的角为 ,
则 ,
直线与平面所成角的正弦值为 .
[素养小结]
向量法求直线与平面所成的角的步骤:
①分析图形中的位置关系,建立空间直角坐标系;
②求出直线的方向向量和平面的法向量 ;
③求出夹角, ;
④判断直线和平面所成的角 和,的关系,求出角 .
拓展 如图,在四棱锥中,侧面 底面 ,侧棱
,底面为直角梯形,其中, ,
, .
(1)求证:平面 .
证明:连接交于,连接,如图. ,
, ,
,, .
又 平面, 平面,平面 .
(2)在棱上是否存在一点,使得与平面所成角的正弦值为 ?若存
在,求出线段 的长度;若不存在,请说明理由.
解:假设在棱上存在一点,使得与平面所成角的正弦值为 ,设
.
取的中点,连接,,,,又 侧面 底面
,侧面 底面, 侧面, 底面 .
,,,为中点, 四边形 为
矩形, .
以为坐标原点,,,所在直线分别为,, 轴建立如图所示的空间直
角坐标系,
则,,,,,则 ,
.
设平面的法向量为 ,
则令,则, ,
平面的一个法向量为 .
,,又 ,
.
设与平面所成的角为 ,
则,,解得或 .
当时, ;
当时, .
故棱上存在一点,使得与平面所成角的正弦值为,且 或
.
探究点三 求平面与平面的夹角
例3 如图,在直三棱柱中, 是边
长为2的正三角形,为 的中点.
(1)证明: 平面 ;
解:证明:是正三角形,为 的中点,
,
在直三棱柱中,可得 平面 ,
又 平面, .
又,, 平面 ,
平面 .
(2)若,求平面与平面 夹角的余弦值.
解:设的中点为,连接,易知, ,
两两垂直,以为坐标原点,,, 所在直
线分别为,, 轴,建立空间直角坐标系,如图.
是边长为2的正三角形,
,则,, ,
,,, , .
设平面的法向量为 ,
则即
取,则,,故,, .
设平面的法向量为 ,
则即
取,则,,故 .
设平面与平面的夹角为 ,则 ,
,
故平面与平面夹角的余弦值为 .
变式 如图所示,在三棱锥中, 为等腰直角三角形,
,为正三角形, .
(1)证明: ;
证明:取的中点,连接, ,如图所示.
为等腰直角三角形,
,又为正三角形, .
, 平面, 平面 ,
平面 .
平面, .
(2)若平面 平面,求平面与平面 的夹角的余弦值.
解: 平面 平面,平面 平面,
平面, ,
平面.以为坐标原点,, ,
所在直线分别为轴、轴、 轴,建立如图所
示的空间直角坐标系,则, ,
,, ,
, , .
设为平面 的法向量,
则即取,得, 平面 的一
个法向量为 .
易知是平面的一个法向量,
设平面与平面 的夹角为 ,,,
, ,
平面与平面的夹角的余弦值为 .
[素养小结]
设,分别是平面 , 的法向量,则向量与 的夹角(或其补角)就是
两个平面的夹角 ,用坐标法的解题步骤如下:
(1)建系:依据几何条件建立适当的空间直角坐标系;
(2)求法向量:在建立的空间直角坐标系下求两个平面的法向量, ;
(3)计算: .
若直线,的方向向量分别为,,平面 , 的法向量分别为, ,则有
(1)线线夹角:若异面直线,的夹角为,则 ;
(2)线面角:若与 所成的角为,则 ;
(3)面面夹角:若 与 的夹角为,则 .
注意:空间两条直线夹角的取值范围与空间两个向量夹角的取值范围不同.二面角
的大小是指两个半平面的张开程度,可以用其平面角 的大小来度量,它的取值范
围为,平面与平面的夹角的取值范围为 .
用空间向量求空间角的过程基本上程序化,求解形式直观,相比传统几何方法具
有优越性.因此,我们应该熟练灵活地应用向量这一工具,快而准地解决立体几何
中有关角的问题.
例1 如图所示,在棱长为的正方体中,,分别是, 的
中点.
解:如图,以为原点,,, 所在
直线分别为轴、轴、 轴,建立如图
所示的空间直角坐标系.
(1)求异面直线与 所成角的余弦值;
解:易知,,,, ,
,
, ,
故异面直线与所成角的余弦值为 .
(2)求直线与平面 所成角的余弦值;
解:由已知得, ,
,则, .
设平面的法向量为 ,
由得令,则平面 的一个法向量为
.
设直线与平面所成的角为,易知 ,则
,, ,
故直线与平面所成角的余弦值为 .
(3)求平面与平面 夹角的余弦值.
解:由(2)知,平面的一个法向量为,易知平面 的一
个法向量为, ,
平面与平面夹角的余弦值为 .
例2 如图,在四棱锥中,底面 是一个
直角梯形,其中 ,, 底面
,,,点和点 分别
为和 的中点.
(1)证明:直线平面 ;
证明:以为原点,的方向为轴正方向,
的方向为轴正方向,的方向为 轴正方向,建立
如图所示的空间直角坐标系,
则,,,, ,
所以, ,
.
设平面的法向量为 ,
则即
取,则 ,
所以,又 平面 ,
所以直线平面 .
(2)求直线与平面 所成角的余弦值;
解:,所以,, ,
设平面的法向量为 ,
则即取,则 .
设直线与平面所成的角为 ,
则 ,
所以 ,
所以直线与平面所成角的余弦值为 .
(3)求平面与平面 的夹角的正弦值.
解:设平面的法向量为 ,
则即
取,得 .
设平面与平面的夹角为 ,
则 ,
所以 ,
所以平面与平面的夹角的正弦值为 .
例3 [2023· 新课标Ⅰ卷] 如图,在正四棱柱
中,,.点,, ,
分别在棱,,,上, ,
, .
(1)证明: ;
①
解:证明:方法一:如图①,作交于 ,
交于,连接,易知 ,且
,所以四边形 是平行四边形,所以
.因为, ,所以四边形
是平行四边形,所以 ,所以
.
方法二:因为
, ,
,,四点不共线,所以 .
(2)点在棱上,当二面角为 时,求 .
②
解:方法一:如图②,以为原点,以,, 所在
直线分别为,, 轴,建立空间直角坐标系,则
,,,设 ,
则, ,
.
设,分别为平面, 的法向量,
则取,得,同理 .
由题得,,整理得 ,
解得或,则 .
③
方法二:如图③,连接,易证四边形 为菱形,
连接,设与相交于点 .
因为二面角为 ,所以直线 与平面
所成的角为 ,
易知,所以点到平面 的距离
.
连接,,,, ,由
,得 ,
由,得 ,
又,所以 平面.因为二面角为,
所以与平面所成的角为 ,易知 ,
所以点到平面的距离.所以 .
又到平面和平面的距离都为2(平面和平面 为同一
个平面),
所以,所以,解得 .
1.4 空间向量的应用
1.4.2 用空间向量研究距离、夹角问题
第2课时 用空间向量研究夹角问题
【学习目标】
1.知道两个相交平面夹角的含义,借助直线的方向向量和平面的法向量,
能求直线与直线、直线与平面所成的角,平面与平面的夹角.
2.能分析和解决一些立体几何中的角度问题,体会向量方法与综合几何方
法的共性和差异,体会直线的方向向量和平面的法向量的作用,感悟向量是研
究几何问题的有效工具.
知识点 空间角
设直线,的方向向量分别为,,平面 , 的法向量分别为, ,则
空间图形 范围 向量法 几何法
异面直线所 成的角 , _____ 平移交于一点,解三
角形
直线与平面 所成的角 _____ _____ _____ , _ _____ 过直线上一点作平面
的垂线,解三角形
空间图形 范围 向量法 几何法
平面与平面 的夹角 _____ _____ _____ , _ ______ 作两平面的垂线,解
三角形
续表
【诊断分析】 判断正误.(请在括号中打“√”或“×”)
(1)异面直线所成的角与其方向向量的夹角相等.( )
×
[解析] 当两个方向向量的夹角是锐角或直角时,向量的夹角与异面直线所成的角相
等;当两个方向向量的夹角为钝角时,向量的夹角与异面直线所成的角互补.故错误.
(2)若平面 的法向量为,直线的方向向量为,直线与平面 所成的角为 ,
则 .( )
×
[解析] ,故错误.
(3)二面角的大小等于平面与平面的夹角.( )
×
[解析] 二面角中不大于 的二面角称为平面与平面的夹角.故错误.
探究点一 异面直线所成角的求法
例1 如图所示,在三棱柱中, 是
正三角形,点在平面上的射影为的中点 ,侧
面是边长为2的菱形,求异面直线与 所成
角的余弦值.
解:如图,连接,,因为点在平面上的射影为的中点 ,
所以 平面,又 平面, 平面,所以 ,
.
因为是正三角形,是的中点,所以 .
以 为原点建立如图所示的空间直角坐标系,则
,,, ,所以
, .
设异面直线与所成的角为 ,
则,即异面直线 与
所成角的余弦值为 .
变式 [2024·重庆巴渝学校高二期中] 如图,在四棱锥
中, 底面,底面 为正方
形,,为上一点,且 ,则异
面直线与 所成的角的大小为( )
B
A. B. C. D.
[解析] 以点D为坐标原点,,, 所在直线
分别为,, 轴,建立如图所示的空间直角坐标
系,则,,, ,
所以, ,所以
, ,所以异面直
线与所成的角的大小为 .故选B.
[素养小结]
用向量法求异面直线所成的角时,常在两异面直线与上分别取点,和 ,
,则与分别为直线,的方向向量,若异面直线,所成的角为 ,则
.
运用向量法常有两种途径:
①基底法:在一些不适合建立空间直角坐标系的题型中,经常采用取基底的方法.
在由公式,求向量,的夹角时,关键是求出,与 ,
一般是把, 用基向量表示出来,再求有关的量.
②坐标法:根据题目条件建立恰当的空间直角坐标系,写出相关各点的坐标,利
用坐标法求异面直线所成的角,避免了传统找角或作角的步骤,使过程变得简
单.
探究点二 求直线和平面所成的角
例2 [2024·浙江浙南名校联盟高二期中] 已知三棱
柱满足 ,
, ,顶点 在平面
上的射影为点 .
(1)证明: 平面 ;
解:证明:由已知得 平面,又 平面,所以 ,
因为 ,所以,又因为 ,
, 平面,所以 平面 .
(2)若点为的中点,点为的中点,求直线与平面 所成角的
正弦值.
解:因为 平面, 平面,所以.在
中, ,所以 ,故 .
如图,以为原点,,所在直线分别为轴, 轴,过点
且与平行的直线为 轴,建立空间直角坐标系,
则,, ,
, ,
所以, .
设平面的法向量为 ,
则即
令,得,,所以平面的一个法向量为 .
设直线与平面所成的角为 ,
又,则 ,所以直线
与平面所成角的正弦值为 .
变式 如图,在四棱锥 中,
, , ,底面
是菱形,是的中点, .
(1)证明:平面 平面 ;
解:证明:如图,连接 ,
底面 是菱形,
且 , 是等边三角形,
又是的中点, .
, .
,, 平面, 平面 ,
又 平面, 平面 平面 .
(2)求直线与平面 所成角的正弦值.
解:, ,, .
底面是菱形,是的中点, ,
,又,,即 .
由(1)知,,, 以为原点,,,
所在直线分别为,, 轴,建立空间直角坐标系,如图,
则,,, ,
,,. 设 是平面
的法向量,
则取,得 .
设直线与平面所成的角为 ,
则 ,
直线与平面所成角的正弦值为 .
[素养小结]
向量法求直线与平面所成的角的步骤:
①分析图形中的位置关系,建立空间直角坐标系;
②求出直线的方向向量和平面的法向量 ;
③求出夹角, ;
④判断直线和平面所成的角 和,的关系,求出角 .
拓展 如图,在四棱锥中,侧面 底面 ,侧棱
,底面为直角梯形,其中, ,
, .
(1)求证:平面 .
证明:连接交于,连接,如图. ,
, ,
,, .
又 平面, 平面,平面 .
(2)在棱上是否存在一点,使得与平面所成角的正弦值为 ?若存
在,求出线段 的长度;若不存在,请说明理由.
解:假设在棱上存在一点,使得与平面所成角的正弦值为 ,设
.
取的中点,连接,,,,又 侧面 底面
,侧面 底面, 侧面, 底面 .
,,,为中点, 四边形 为
矩形, .
以为坐标原点,,,所在直线分别为,, 轴建立如图所示的空间直
角坐标系,
则,,,,,则 ,
.
设平面的法向量为 ,
则令,则, ,
平面的一个法向量为 .
,,又 ,
.
设与平面所成的角为 ,
则,,解得或 .
当时, ;
当时, .
故棱上存在一点,使得与平面所成角的正弦值为,且 或
.
探究点三 求平面与平面的夹角
例3 如图,在直三棱柱中, 是边
长为2的正三角形,为 的中点.
(1)证明: 平面 ;
解:证明:是正三角形,为 的中点,
,
在直三棱柱中,可得 平面 ,
又 平面, .
又,, 平面 ,
平面 .
(2)若,求平面与平面 夹角的余弦值.
解:设的中点为,连接,易知, ,
两两垂直,以为坐标原点,,, 所在直
线分别为,, 轴,建立空间直角坐标系,如图.
是边长为2的正三角形,
,则,, ,
,,, , .
设平面的法向量为 ,
则即
取,则,,故,, .
设平面的法向量为 ,
则即
取,则,,故 .
设平面与平面的夹角为 ,则 ,
,
故平面与平面夹角的余弦值为 .
变式 如图所示,在三棱锥中, 为等腰直角三角形,
,为正三角形, .
(1)证明: ;
证明:取的中点,连接, ,如图所示.
为等腰直角三角形,
,又为正三角形, .
, 平面, 平面 ,
平面 .
平面, .
(2)若平面 平面,求平面与平面 的夹角的余弦值.
解: 平面 平面,平面 平面,
平面, ,
平面.以为坐标原点,, ,
所在直线分别为轴、轴、 轴,建立如图所
示的空间直角坐标系,则, ,
,, ,
, , .
设为平面 的法向量,
则即取,得, 平面 的一
个法向量为 .
易知是平面的一个法向量,
设平面与平面 的夹角为 ,,,
, ,
平面与平面的夹角的余弦值为 .
[素养小结]
设,分别是平面 , 的法向量,则向量与 的夹角(或其补角)就是
两个平面的夹角 ,用坐标法的解题步骤如下:
(1)建系:依据几何条件建立适当的空间直角坐标系;
(2)求法向量:在建立的空间直角坐标系下求两个平面的法向量, ;
(3)计算: .
若直线,的方向向量分别为,,平面 , 的法向量分别为, ,则有
(1)线线夹角:若异面直线,的夹角为,则 ;
(2)线面角:若与 所成的角为,则 ;
(3)面面夹角:若 与 的夹角为,则 .
注意:空间两条直线夹角的取值范围与空间两个向量夹角的取值范围不同.二面角
的大小是指两个半平面的张开程度,可以用其平面角 的大小来度量,它的取值范
围为,平面与平面的夹角的取值范围为 .
用空间向量求空间角的过程基本上程序化,求解形式直观,相比传统几何方法具
有优越性.因此,我们应该熟练灵活地应用向量这一工具,快而准地解决立体几何
中有关角的问题.
例1 如图所示,在棱长为的正方体中,,分别是, 的
中点.
解:如图,以为原点,,, 所在
直线分别为轴、轴、 轴,建立如图
所示的空间直角坐标系.
(1)求异面直线与 所成角的余弦值;
解:易知,,,, ,
,
, ,
故异面直线与所成角的余弦值为 .
(2)求直线与平面 所成角的余弦值;
解:由已知得, ,
,则, .
设平面的法向量为 ,
由得令,则平面 的一个法向量为
.
设直线与平面所成的角为,易知 ,则
,, ,
故直线与平面所成角的余弦值为 .
(3)求平面与平面 夹角的余弦值.
解:由(2)知,平面的一个法向量为,易知平面 的一
个法向量为, ,
平面与平面夹角的余弦值为 .
例2 如图,在四棱锥中,底面 是一个
直角梯形,其中 ,, 底面
,,,点和点 分别
为和 的中点.
(1)证明:直线平面 ;
证明:以为原点,的方向为轴正方向,
的方向为轴正方向,的方向为 轴正方向,建立
如图所示的空间直角坐标系,
则,,,, ,
所以, ,
.
设平面的法向量为 ,
则即
取,则 ,
所以,又 平面 ,
所以直线平面 .
(2)求直线与平面 所成角的余弦值;
解:,所以,, ,
设平面的法向量为 ,
则即取,则 .
设直线与平面所成的角为 ,
则 ,
所以 ,
所以直线与平面所成角的余弦值为 .
(3)求平面与平面 的夹角的正弦值.
解:设平面的法向量为 ,
则即
取,得 .
设平面与平面的夹角为 ,
则 ,
所以 ,
所以平面与平面的夹角的正弦值为 .
例3 [2023· 新课标Ⅰ卷] 如图,在正四棱柱
中,,.点,, ,
分别在棱,,,上, ,
, .
(1)证明: ;
①
解:证明:方法一:如图①,作交于 ,
交于,连接,易知 ,且
,所以四边形 是平行四边形,所以
.因为, ,所以四边形
是平行四边形,所以 ,所以
.
方法二:因为
, ,
,,四点不共线,所以 .
(2)点在棱上,当二面角为 时,求 .
②
解:方法一:如图②,以为原点,以,, 所在
直线分别为,, 轴,建立空间直角坐标系,则
,,,设 ,
则, ,
.
设,分别为平面, 的法向量,
则取,得,同理 .
由题得,,整理得 ,
解得或,则 .
③
方法二:如图③,连接,易证四边形 为菱形,
连接,设与相交于点 .
因为二面角为 ,所以直线 与平面
所成的角为 ,
易知,所以点到平面 的距离
.
连接,,,, ,由
,得 ,
由,得 ,
又,所以 平面.因为二面角为,
所以与平面所成的角为 ,易知 ,
所以点到平面的距离.所以 .
又到平面和平面的距离都为2(平面和平面 为同一
个平面),
所以,所以,解得 .
