1.4.1 用空间向量研究直线、平面的位置关系-第2课时课件(共33张PPT)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.4.1 用空间向量研究直线、平面的位置关系-第2课时课件(共33张PPT)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 11:31:24 | ||
图片预览










文档简介
(共33张PPT)
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
第2课时 空间中直线、平面的平行
◆课前预习
◆课中探究
◆备课素材
◆练习册
【学习目标】
1.能用直线的方向向量和平面的法向量刻画直线与直线、直线与平面、平
面与平面的平行.
2.能分析和解决一些立体几何中有关平行的问题,体会向量方法与综合几
何方法的共性和差异,体会直线的方向向量和平面的法向量的作用,感悟向量
是研究几何问题的有效工具.
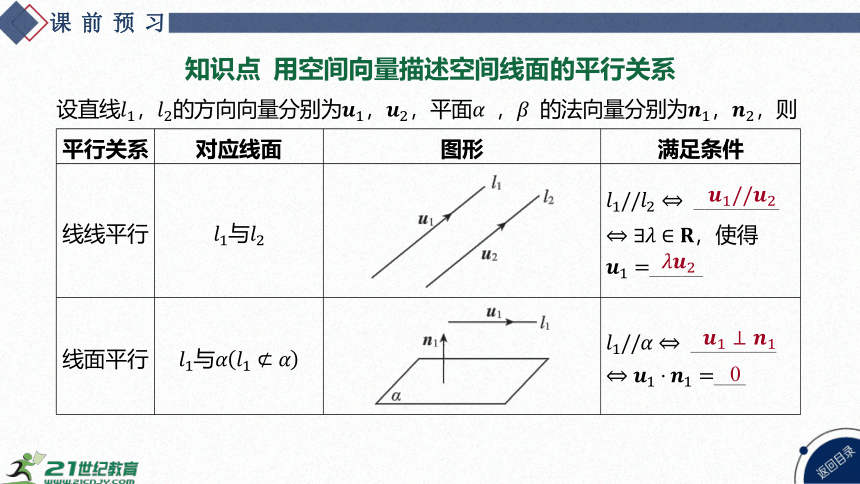
知识点 用空间向量描述空间线面的平行关系
设直线,的方向向量分别为,,平面 , 的法向量分别为, ,则
平行关系 对应线面 图形 满足条件
线线平行 与 ________
,使得
_____
线面平行 与 ________
___
0
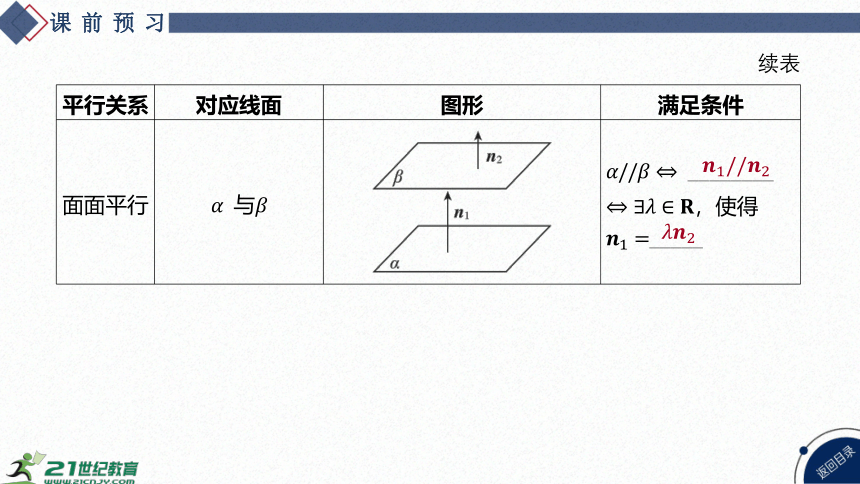
平行关系 对应线面 图形 满足条件
面面平行 与 ________
,使得
_____
续表
【诊断分析】判断正误.(请在括号中打“√”或“×”)
(1)若两条直线平行,则它们的方向向量的方向相同或相反.( )
√
[解析] 若两条直线平行,则它们的方向向量也平行,故它们的方向向量的方向相同
或相反.
(2)若平面外的一条直线的方向向量与平面的法向量垂直,则该直线与平面平
行.( )
√
[解析] 由线面平行的判定定理知,若平面外的一条直线的方向向量与平面的法向
量垂直,则该直线与平面平行.
(3)若两条不同直线,的方向向量分别为, ,则
.( )
√
[解析] 因为,所以 .
(4)若两个平面平行,则这两个平面的法向量一定平行.( )
√
[解析] 若两个平面平行,则这两个平面的法向量一定平行.故正确.
探究点一 空间向量与平行关系
例1(1) 已知直线的一个方向向量,平面 的一个法向量
,则直线与平面 的位置关系是( )
D
A. B. C. D. 或
[解析] 直线的一个方向向量,平面 的一个法向量
,, 或 .故选D.
(2)已知向量,平面 的一个法向量,若 ,
则( )
C
A., B.,
C. D.
[解析] 因为 ,所以,则 ,故选C.
(3)设向量 ,分别是平面 , 的法向量,向量 ,
,若 , 平行,则实数 ___.
4
[解析] , 平面 , 的法向量互相平行, ,
且,解得, .
变式 (多选题)[2024·嘉兴八校高二期中] 下列结论中正确的是( )
ACD
A.若直线的一个方向向量是,直线 的一个方向向量是
,且两条直线不重合,则
B.若直线的一个方向向量是,平面 的一个法向量是 ,
则
C.若平面 , 是空间中两个不同的平面,且平面 的一个法向量是
,平面 的一个法向量是,则
D.若平面 经过三点,,,向量 是平
面 的一个法向量,则
[解析] 因为,,所以,所以, 共线,又直
线,不重合,所以,故A正确;
因为直线 的一个方向向量是,平面 的一个法向量是,
且,所以 ,故B不正确;
因为,,所以,所以 ,故C正确;
因为平面 经过三点,, ,所以,
,又向量是平面 的一个法向量,所以
所以则解得则 ,故D正
确.故选 .
探究点二 利用空间向量证明平行关系
例2 [2024·福州高二期中] 如图,在四棱锥 中,
底面为直角梯形,其中, ,
,, 平面,且,点
在棱上,且,为 的中点.证明:直线
平面 .
证明:如图所示,以为原点,,,所在直线分别为, ,
轴,建立空间直角坐标系,则,, ,
,所以 ,
因为 平面, 平面,所以 ,
又因为,,, 平面 ,所以
平面,所以平面的一个法向量为 .
又,所以 ,
又 平面,所以平面 .
变式 如图所示,四边形为矩形, 平面,, ,
,分别是,, 的中点.求证:
(1)平面 ;
证明:如图所示,以为原点,以,, 所在
直线分别为轴、轴、 轴,建立空间直角坐标系,
设,,则, ,
,,,
因为,, 分别是,, 的中点,
所以,, ,
所以,易知平面 的一个法向量为,
所以,即 .
又 平面,所以平面 .
(2)平面平面 .
解:因为,所以,所以 ,
又 平面,所以平面 .
又,, 平面,所以平面平面 .
[素养小结]
证明线、面平行问题的方法:
(1)用向量法证明线面平行:①证明直线的方向向量与平面内的某一向量是共
线向量且直线不在平面内;②证明直线的方向向量可以用平面内两个不共线向
量表示,且直线不在平面内;③证明直线的方向向量与平面的法向量垂直且直线
不在平面内.
(2)利用空间向量证明面面平行,通常是证明两平面的法向量平行.
拓展 如图,在多面体中,平面
平面,四边形为正方形,四边形
为梯形,且, 是边长为1的等边三角
解:存在,理由如下:
平面 平面,四边形 为正方形,
平面 .
过点作于点 .
形,.线段上是否存在点(不包括端点),使得直线平面 ?若
存在,求出 的值;若不存在,请说明理由.
如图,以点为原点,建立空间直角坐标系,则 ,
, ,
,,, ,
,, ,
设 ,,则 ,
则 ,
设是平面 的法向量,
则即
取,则,是平面
的一个法向量,
由,得,符合题意,即存在点 ,使得直线
平面,此时 .
空间平行关系的向量表示
(1)线线平行
设直线,的方向向量分别为, ,则
,使得,, .
(2)线面平行
设直线的方向向量为,平面 的法向量为 ,
,则 .
(3)面面平行
设平面 , 的法向量分别为, ,则
,使得,, .
空间平行关系的解题策略
几何法 向量法
线线 平行 对于直线,,和平面 , , (1)若,,则 ; (2)若 , ,则 ; (3)若 , ,,则 若直线, 的方向向量
共线,则
线面 平行 对于直线,和平面 , (1)若 ,, ,则 ; (2)若 , ,,则 若直线 的方向向量与平
面 的法向量垂直且
,则
几何法 向量法
面面 平行 对于直线,和平面 , , (1)若 , , , , 且,则 ; (2)若 , ,则 若平面 , 的法向量
共线,则
续表
例1 已知空间中两个有一条公共边的正方形与正方形,设, 分
别是,的中点,给出如下结论:;平面; ;
, 为异面直线.其中所有正确结论的序号为________.
①②③
[解析] 如图所示,设,, ,则
且.连接,则为
的中点,可得
,
则 ,故
,故①正确.,故, 又 平面, 平
面,所以平面 ,故②③正确,④不正确.
例2 [2024·湖北孝感一中高二期中] 如图,在四棱锥
中,底面是正方形, 平面 ,
,是 的中点.
(1)证明:平面 .
解:证明:以为坐标原点,,,的方向分别为 轴、
轴、 轴的正方向建立如图所示的空间直角坐标系.
连接,交于,连接 .
设,依题意得,, .因为底面
是正方形,
所以是此正方形的中心,故点的坐标为 ,
所以, ,
则,所以,故.又 平面 ,
平面 ,
所以平面 .
(2)若点在棱上,且,为棱上一点,试问当 在何位置
时,满足平面 ?
解:因为,所以,又, ,所以
, .
设平面的法向量为 ,
则即令,则,,故 .
因为,,,所以, ,
设 ,
则,又因为平面 ,
所以,即,解得 ,
所以当点为棱的中点时,满足平面 .
例3 如图,在平面内,四边形是边长为2的正方形,四边形 和四
边形都是正方形.将两个正方形分别沿,折起,使与 重合于点
,设直线过点且垂直于正方形所在的平面,点是直线 上的一个动
点,且与点位于平面同侧,设 .
当时,在线段上是否存在点,使平面平面 ?若存在,求
出 的值;若不存在,请说明理由.
解:以为原点,,,所在直线分别为轴、轴、 轴,建立空间直角坐
标系,则,,,,, ,
假设存在满足题意的点 ,
设,则 ,
解得,,,即 ,
所以 .
设平面的法向量为,, ,
, ,
即解得
令,则,所以 .
由平面平面,得平面 ,
所以,即,可得 ,
所以在线段上存在点,使平面平面 ,
此时 .
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
第2课时 空间中直线、平面的平行
◆课前预习
◆课中探究
◆备课素材
◆练习册
【学习目标】
1.能用直线的方向向量和平面的法向量刻画直线与直线、直线与平面、平
面与平面的平行.
2.能分析和解决一些立体几何中有关平行的问题,体会向量方法与综合几
何方法的共性和差异,体会直线的方向向量和平面的法向量的作用,感悟向量
是研究几何问题的有效工具.
知识点 用空间向量描述空间线面的平行关系
设直线,的方向向量分别为,,平面 , 的法向量分别为, ,则
平行关系 对应线面 图形 满足条件
线线平行 与 ________
,使得
_____
线面平行 与 ________
___
0
平行关系 对应线面 图形 满足条件
面面平行 与 ________
,使得
_____
续表
【诊断分析】判断正误.(请在括号中打“√”或“×”)
(1)若两条直线平行,则它们的方向向量的方向相同或相反.( )
√
[解析] 若两条直线平行,则它们的方向向量也平行,故它们的方向向量的方向相同
或相反.
(2)若平面外的一条直线的方向向量与平面的法向量垂直,则该直线与平面平
行.( )
√
[解析] 由线面平行的判定定理知,若平面外的一条直线的方向向量与平面的法向
量垂直,则该直线与平面平行.
(3)若两条不同直线,的方向向量分别为, ,则
.( )
√
[解析] 因为,所以 .
(4)若两个平面平行,则这两个平面的法向量一定平行.( )
√
[解析] 若两个平面平行,则这两个平面的法向量一定平行.故正确.
探究点一 空间向量与平行关系
例1(1) 已知直线的一个方向向量,平面 的一个法向量
,则直线与平面 的位置关系是( )
D
A. B. C. D. 或
[解析] 直线的一个方向向量,平面 的一个法向量
,, 或 .故选D.
(2)已知向量,平面 的一个法向量,若 ,
则( )
C
A., B.,
C. D.
[解析] 因为 ,所以,则 ,故选C.
(3)设向量 ,分别是平面 , 的法向量,向量 ,
,若 , 平行,则实数 ___.
4
[解析] , 平面 , 的法向量互相平行, ,
且,解得, .
变式 (多选题)[2024·嘉兴八校高二期中] 下列结论中正确的是( )
ACD
A.若直线的一个方向向量是,直线 的一个方向向量是
,且两条直线不重合,则
B.若直线的一个方向向量是,平面 的一个法向量是 ,
则
C.若平面 , 是空间中两个不同的平面,且平面 的一个法向量是
,平面 的一个法向量是,则
D.若平面 经过三点,,,向量 是平
面 的一个法向量,则
[解析] 因为,,所以,所以, 共线,又直
线,不重合,所以,故A正确;
因为直线 的一个方向向量是,平面 的一个法向量是,
且,所以 ,故B不正确;
因为,,所以,所以 ,故C正确;
因为平面 经过三点,, ,所以,
,又向量是平面 的一个法向量,所以
所以则解得则 ,故D正
确.故选 .
探究点二 利用空间向量证明平行关系
例2 [2024·福州高二期中] 如图,在四棱锥 中,
底面为直角梯形,其中, ,
,, 平面,且,点
在棱上,且,为 的中点.证明:直线
平面 .
证明:如图所示,以为原点,,,所在直线分别为, ,
轴,建立空间直角坐标系,则,, ,
,所以 ,
因为 平面, 平面,所以 ,
又因为,,, 平面 ,所以
平面,所以平面的一个法向量为 .
又,所以 ,
又 平面,所以平面 .
变式 如图所示,四边形为矩形, 平面,, ,
,分别是,, 的中点.求证:
(1)平面 ;
证明:如图所示,以为原点,以,, 所在
直线分别为轴、轴、 轴,建立空间直角坐标系,
设,,则, ,
,,,
因为,, 分别是,, 的中点,
所以,, ,
所以,易知平面 的一个法向量为,
所以,即 .
又 平面,所以平面 .
(2)平面平面 .
解:因为,所以,所以 ,
又 平面,所以平面 .
又,, 平面,所以平面平面 .
[素养小结]
证明线、面平行问题的方法:
(1)用向量法证明线面平行:①证明直线的方向向量与平面内的某一向量是共
线向量且直线不在平面内;②证明直线的方向向量可以用平面内两个不共线向
量表示,且直线不在平面内;③证明直线的方向向量与平面的法向量垂直且直线
不在平面内.
(2)利用空间向量证明面面平行,通常是证明两平面的法向量平行.
拓展 如图,在多面体中,平面
平面,四边形为正方形,四边形
为梯形,且, 是边长为1的等边三角
解:存在,理由如下:
平面 平面,四边形 为正方形,
平面 .
过点作于点 .
形,.线段上是否存在点(不包括端点),使得直线平面 ?若
存在,求出 的值;若不存在,请说明理由.
如图,以点为原点,建立空间直角坐标系,则 ,
, ,
,,, ,
,, ,
设 ,,则 ,
则 ,
设是平面 的法向量,
则即
取,则,是平面
的一个法向量,
由,得,符合题意,即存在点 ,使得直线
平面,此时 .
空间平行关系的向量表示
(1)线线平行
设直线,的方向向量分别为, ,则
,使得,, .
(2)线面平行
设直线的方向向量为,平面 的法向量为 ,
,则 .
(3)面面平行
设平面 , 的法向量分别为, ,则
,使得,, .
空间平行关系的解题策略
几何法 向量法
线线 平行 对于直线,,和平面 , , (1)若,,则 ; (2)若 , ,则 ; (3)若 , ,,则 若直线, 的方向向量
共线,则
线面 平行 对于直线,和平面 , (1)若 ,, ,则 ; (2)若 , ,,则 若直线 的方向向量与平
面 的法向量垂直且
,则
几何法 向量法
面面 平行 对于直线,和平面 , , (1)若 , , , , 且,则 ; (2)若 , ,则 若平面 , 的法向量
共线,则
续表
例1 已知空间中两个有一条公共边的正方形与正方形,设, 分
别是,的中点,给出如下结论:;平面; ;
, 为异面直线.其中所有正确结论的序号为________.
①②③
[解析] 如图所示,设,, ,则
且.连接,则为
的中点,可得
,
则 ,故
,故①正确.,故, 又 平面, 平
面,所以平面 ,故②③正确,④不正确.
例2 [2024·湖北孝感一中高二期中] 如图,在四棱锥
中,底面是正方形, 平面 ,
,是 的中点.
(1)证明:平面 .
解:证明:以为坐标原点,,,的方向分别为 轴、
轴、 轴的正方向建立如图所示的空间直角坐标系.
连接,交于,连接 .
设,依题意得,, .因为底面
是正方形,
所以是此正方形的中心,故点的坐标为 ,
所以, ,
则,所以,故.又 平面 ,
平面 ,
所以平面 .
(2)若点在棱上,且,为棱上一点,试问当 在何位置
时,满足平面 ?
解:因为,所以,又, ,所以
, .
设平面的法向量为 ,
则即令,则,,故 .
因为,,,所以, ,
设 ,
则,又因为平面 ,
所以,即,解得 ,
所以当点为棱的中点时,满足平面 .
例3 如图,在平面内,四边形是边长为2的正方形,四边形 和四
边形都是正方形.将两个正方形分别沿,折起,使与 重合于点
,设直线过点且垂直于正方形所在的平面,点是直线 上的一个动
点,且与点位于平面同侧,设 .
当时,在线段上是否存在点,使平面平面 ?若存在,求
出 的值;若不存在,请说明理由.
解:以为原点,,,所在直线分别为轴、轴、 轴,建立空间直角坐
标系,则,,,,, ,
假设存在满足题意的点 ,
设,则 ,
解得,,,即 ,
所以 .
设平面的法向量为,, ,
, ,
即解得
令,则,所以 .
由平面平面,得平面 ,
所以,即,可得 ,
所以在线段上存在点,使平面平面 ,
此时 .
