1.4.2 用空间向量研究距离、夹角问题-第1课时课件(共40张PPT)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.4.2 用空间向量研究距离、夹角问题-第1课时课件(共40张PPT)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 00:00:00 | ||
图片预览











文档简介
(共40张PPT)
1.4 空间向量的应用
1.4.2 用空间向量研究距离、夹角问题
第1课时 用空间向量研究距离问题
【学习目标】
1.借助直线的方向向量和平面的法向量,能计算点到直线的距离、点到平
面的距离,并知道两条平行直线之间的距离、直线与平面平行时两者间的距离、
两个平行平面之间的距离.
2.能分析和解决一些立体几何中的距离问题,体会向量方法与综合几何方
法的共性和差异,体会直线的方向向量和平面的法向量的作用,感悟向量是研
究几何问题的有效工具.
知识点 用空间向量研究距离问题
1.点到直线的距离
如图,已知直线的单位方向向量为,是直线上的定点,是直线 外一点,
设,则向量在直线上的投影向量.在 中,由勾
股定理,得_ ______________ ______________.
2.点到平面的距离
如图,已知平面 的法向量为,是平面 内的定
点,是平面 外一点.过点作平面 的垂线 ,交平
面 于点,则是直线的方向向量,且点到平面 的
距离就是在直线上的投影向量 的长度.因此
_ ______ ______.
3.用空间向量解决立体几何问题的“三步曲”
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、
平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离
和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
【诊断分析】 判断正误.(请在括号中打“√”或“×”)
(1)平面 外一点到平面 的距离,就是点与平面 内一点所成向量 的
长度.( )
×
(2)若直线平面 ,则直线到平面 的距离就是直线上的点到平面 的
距离.( )
√
(3)若平面平面 ,则两平面 , 的距离可转化为平面 内某条直线到
平面 的距离,也可转化为平面 内某点到平面 的距离.( )
√
探究点一 点到直线的距离
例1(1) [2024·重庆开州中学高二月考]已知直线过点,直线 的一
个方向向量为,则到直线 的距离等于( )
C
A. B. C. D.5
[解析] 连接,,, ,
,所以到直线 的距离为
.故选C.
(2)[2024·江苏淮安高二期中]已知四棱锥的底面为正方形, 平
面,,点是的中点,则点到直线 的距离是( )
D
A. B. C. D.
[解析] 连接 ,如图,以A为原点,建立空间直角
坐标系,则,, ,所以
,,所以 ,
,,所以点到直线 的
距离是 .故选D.
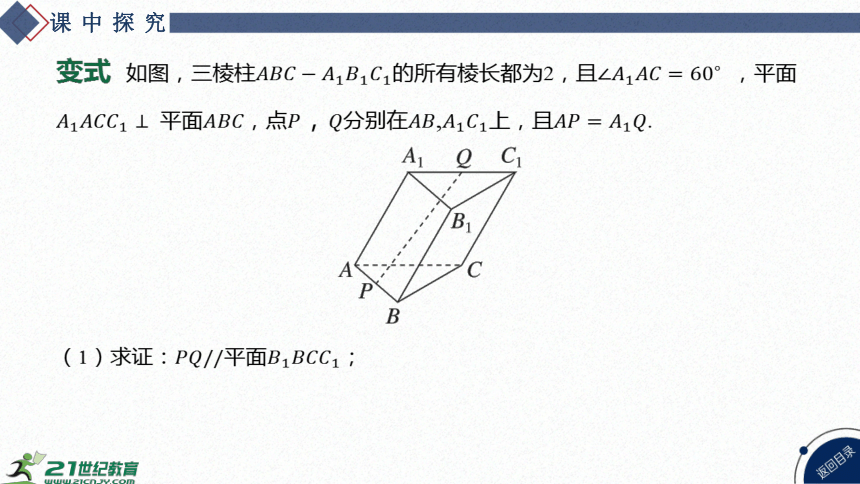
变式 如图,三棱柱的所有棱长都为2,且 ,平面
平面,点,分别在,上,且 .
(1)求证:平面 ;
解:证明:如图,作,交于点 ,则由
,得 ,
,,即, 且
,连接 ,
四边形 为平行四边形,
平面,且 平面 ,
平面 .
(2)当点是棱的中点时,求点到直线 的距离.
解:取的中点,连接, ,
,, , 根据余弦定理得
,
,
则,又平面 平面,平面 平面 ,
平面 .
是等边三角形, ,建立如图所示的空间
直角坐标系,则,, ,
,, ,
, ,
,, 点到直线
的距离为,
.
[素养小结]
用向量法求点到直线的距离的一般步骤:
(1)建立空间直角坐标系;
(2)求直线的方向向量;
(3)计算所求点与直线上某一点所构成的向量在直线上的投影向量的长度;
(4)利用勾股定理求解.
另外,要注意平行直线间的距离与点到直线的距离之间的转化.
探究点二 点到平面的距离
例2 如图所示,在四棱锥中,四边形 为
正方形, 平面,,, 分别
为, 的中点.
(1)求证:平面 ;
解:证明:以为原点,,, 所在直线分别
为轴、轴、 轴,建立如图所示的空间直角坐标系,
则,,,, ,
所以,, ,
所以 ,
又因为 平面,所以平面 .
(2)求点到平面 的距离.
解:由(1)可知,平面,所以点到平面的距离等于点 到平
面 的距离.
设平面的法向量为 ,
则即取,得 .
因为,所以点到平面的距离,所以点
到平面的距离为 .
变式 [2024·广西玉林高二期中] 如图,在四棱锥
中,底面是正方形, 底面
,,点是棱的中点,点 是棱
上靠近点 的三等分点.
(1)证明: ;
解:证明:因为 底面, 底面
,所以,又, ,
, 平面,所以 平面,又
平面,所以.因为,点 是棱
的中点,所以 ,
又,, 平面,所以 平
面,又 平面,所以 .
(2)求点到平面 的距离.
解:由题意知,,两两垂直,如图,以点
为原点建立空间直角坐标系,则, ,
, ,
故,, .
设平面的法向量为 ,
则令,则, ,
所以是平面 的一个法向量,所以
点到平面的距离为 .
[素养小结]
用向量法求点到平面的距离的步骤:
(1)建系:建立恰当的空间直角坐标系;
(2)求点的坐标:写出(求出)相关点的坐标;
(3)求向量:求出相关向量的坐标;
(4)利用公式即可求得点到平面的距离.
拓展 如图①,平行四边形由一个边长为6的正方形(正方形 )和2
个等腰直角三角形组成,沿, 将2个三角形折起,使得平
面、平面均与平面垂直(如图②),连接,,, ,
求点到平面 的距离.
①
②
解:因为平面 平面,平面 平面, ,
平面 ,所以 平面 ,
又因为 平面 ,
所以,又因为 , 所以,,两两垂直
以为原点,,,
所在直线分别为轴、轴、 轴,建立如图所示的空
间直角坐标系,
则,,, ,
所以,, .
设平面的法向量为,则
所以即
令,则,,所以是平面 的一个法向量.
设点到平面的距离为 ,
则,所以点到平面的距离为 .
探究点三 线面距和面面距
例3 如图,在四棱锥中,底面 是边长
为2的正方形, 底面,,, ,
分别是,, 的中点.求:
(1)直线到平面 的距离;
解:因为 平面,四边形 为正方形,
所以,,两两垂直.以点为坐标原点,,,
所在直线分别为,, 轴建立如图所示的空间直角坐标系,
则,,, .
因为,分别为,的中点,所以 ,
又因为 平面, 平面,所以平面 .
因为且,,分别为,的中点,所以且 ,
所以四边形为平行四边形,所以 .
因为 平面, 平面 ,
所以平面 .
因为,, 平面 ,
所以平面平面 .
因为 平面,所以平面,所以直线到平面 的距离等于
点到平面 的距离.
设平面的法向量为 ,
又, ,
则取,可得 ,
又,所以直线到平面 的距离
.
(2)平面与平面 的距离.
解:由(1)知平面平面,所以平面与平面 的距离
.
变式 设正方体 的棱长为2.
(1)求直线到平面 的距离;
解:以为原点,,,所在直线分别为,,
轴,建立如图所示的空间直角坐标系,
则,,,, ,
所以,, ,所以
,即 ,
又 平面, 平面,所以 平面
,所以直线到平面的距离等于点到平面 的距离.
设平面的法向量为 ,
则令,则 ,
又 ,
所以点到平面的距离,即直线到平面 的
距离为 .
(2)求平面与平面 的距离.
解:由(1)知平面,同理可得平面 ,又
,, 平面 ,
所以平面平面,即平面与平面的距离等于点 到平面
的距离.
由(1)知,点到平面的距离 ,
所以平面与平面的距离为 .
[素养小结]
(1)求线面距离可以转化为求直线上任意一点到平面的距离,利用求点到平面
的距离的方法求解即可.
(2)求两个平行平面间的距离可以转化为求点到平面的距离,利用求点到平面
的距离的方法求解即可.
1.四种类型的距离求法
距离类型 求解(转化)方法
点到直线 的距离 已知直线外一点,直线过点,直线的单位方向向量为 ,设
,则点到直线的距离
点到平面 的距离 已知平面 外一点,为平面 上一点,且 的一个法向量为 ,则点
到平面 的距离
线面距离 线面距离可以转化为点面距离求解
面面距离 面面距离可以转化为点面距离求解
2.用空间向量解决立体几何问题可用两种方法
(1)向量法:可具体表示为“设基底——巧运算——译结果”,其中设不共线的三
个向量构成空间的一个基底,并把相关向量用基底表示出来是关键.
(2)坐标法:可具体表示为“建系设点——巧运算——译结果”,其中建立适当的
空间直角坐标系,并确定相关点的坐标是关键.
1.求点到直线的距离,一般先计算所求点与直线上某一点所构成的向量在直线
上的投影向量的长度,再利用勾股定理求解.
例1 (多选题)在空间直角坐标系中,,, ,
则下列结论正确的是( )
BD
A.
B.点到平面 的距离是2
C.异面直线与所成角的余弦值为
D.点到直线的距离是
[解析] 因为,,所以 ,故A错误.
在空间直角坐标系中,结合A与C两点的坐标可知轴与平面 垂直,所以
为平面的一个法向量,则点B到平面的距离是 ,
故B正确.
因为,,所以异面直线与 所成角的余弦值
为,故C错误.
因为,所以,所以点到直线 的距离是
,故D正确.故选 .
2.空间线面、面面距离问题一般转化为点面距离问题解决.若点为平面 外一
点,点为平面 内任意一点,平面 的法向量为,则点到平面 的距离
.
例2 [2024·甘肃张掖高二期中] 如图,正方体
的棱长为2,点为 的中点.
(1)求点到平面 的距离;
解:以为原点,,,所在的直线分别为,,
轴建立如图所示的空间直角坐标系,
则,,, ,
所以, .
设平面的法向量为 ,
则
令,则, ,
所以平面的一个法向量为 .
又 ,
所以点到平面的距离为 .
(2)求到平面 的距离.
解:由(1)可得平面的一个法向量为 ,
因为,,所以 ,
所以 ,
所以,又 平面 ,
所以平面 ,
所以到平面的距离可以转化为点到平面 的距离.
又 ,
所以到平面的距离为 .
1.4 空间向量的应用
1.4.2 用空间向量研究距离、夹角问题
第1课时 用空间向量研究距离问题
【学习目标】
1.借助直线的方向向量和平面的法向量,能计算点到直线的距离、点到平
面的距离,并知道两条平行直线之间的距离、直线与平面平行时两者间的距离、
两个平行平面之间的距离.
2.能分析和解决一些立体几何中的距离问题,体会向量方法与综合几何方
法的共性和差异,体会直线的方向向量和平面的法向量的作用,感悟向量是研
究几何问题的有效工具.
知识点 用空间向量研究距离问题
1.点到直线的距离
如图,已知直线的单位方向向量为,是直线上的定点,是直线 外一点,
设,则向量在直线上的投影向量.在 中,由勾
股定理,得_ ______________ ______________.
2.点到平面的距离
如图,已知平面 的法向量为,是平面 内的定
点,是平面 外一点.过点作平面 的垂线 ,交平
面 于点,则是直线的方向向量,且点到平面 的
距离就是在直线上的投影向量 的长度.因此
_ ______ ______.
3.用空间向量解决立体几何问题的“三步曲”
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、
平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离
和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
【诊断分析】 判断正误.(请在括号中打“√”或“×”)
(1)平面 外一点到平面 的距离,就是点与平面 内一点所成向量 的
长度.( )
×
(2)若直线平面 ,则直线到平面 的距离就是直线上的点到平面 的
距离.( )
√
(3)若平面平面 ,则两平面 , 的距离可转化为平面 内某条直线到
平面 的距离,也可转化为平面 内某点到平面 的距离.( )
√
探究点一 点到直线的距离
例1(1) [2024·重庆开州中学高二月考]已知直线过点,直线 的一
个方向向量为,则到直线 的距离等于( )
C
A. B. C. D.5
[解析] 连接,,, ,
,所以到直线 的距离为
.故选C.
(2)[2024·江苏淮安高二期中]已知四棱锥的底面为正方形, 平
面,,点是的中点,则点到直线 的距离是( )
D
A. B. C. D.
[解析] 连接 ,如图,以A为原点,建立空间直角
坐标系,则,, ,所以
,,所以 ,
,,所以点到直线 的
距离是 .故选D.
变式 如图,三棱柱的所有棱长都为2,且 ,平面
平面,点,分别在,上,且 .
(1)求证:平面 ;
解:证明:如图,作,交于点 ,则由
,得 ,
,,即, 且
,连接 ,
四边形 为平行四边形,
平面,且 平面 ,
平面 .
(2)当点是棱的中点时,求点到直线 的距离.
解:取的中点,连接, ,
,, , 根据余弦定理得
,
,
则,又平面 平面,平面 平面 ,
平面 .
是等边三角形, ,建立如图所示的空间
直角坐标系,则,, ,
,, ,
, ,
,, 点到直线
的距离为,
.
[素养小结]
用向量法求点到直线的距离的一般步骤:
(1)建立空间直角坐标系;
(2)求直线的方向向量;
(3)计算所求点与直线上某一点所构成的向量在直线上的投影向量的长度;
(4)利用勾股定理求解.
另外,要注意平行直线间的距离与点到直线的距离之间的转化.
探究点二 点到平面的距离
例2 如图所示,在四棱锥中,四边形 为
正方形, 平面,,, 分别
为, 的中点.
(1)求证:平面 ;
解:证明:以为原点,,, 所在直线分别
为轴、轴、 轴,建立如图所示的空间直角坐标系,
则,,,, ,
所以,, ,
所以 ,
又因为 平面,所以平面 .
(2)求点到平面 的距离.
解:由(1)可知,平面,所以点到平面的距离等于点 到平
面 的距离.
设平面的法向量为 ,
则即取,得 .
因为,所以点到平面的距离,所以点
到平面的距离为 .
变式 [2024·广西玉林高二期中] 如图,在四棱锥
中,底面是正方形, 底面
,,点是棱的中点,点 是棱
上靠近点 的三等分点.
(1)证明: ;
解:证明:因为 底面, 底面
,所以,又, ,
, 平面,所以 平面,又
平面,所以.因为,点 是棱
的中点,所以 ,
又,, 平面,所以 平
面,又 平面,所以 .
(2)求点到平面 的距离.
解:由题意知,,两两垂直,如图,以点
为原点建立空间直角坐标系,则, ,
, ,
故,, .
设平面的法向量为 ,
则令,则, ,
所以是平面 的一个法向量,所以
点到平面的距离为 .
[素养小结]
用向量法求点到平面的距离的步骤:
(1)建系:建立恰当的空间直角坐标系;
(2)求点的坐标:写出(求出)相关点的坐标;
(3)求向量:求出相关向量的坐标;
(4)利用公式即可求得点到平面的距离.
拓展 如图①,平行四边形由一个边长为6的正方形(正方形 )和2
个等腰直角三角形组成,沿, 将2个三角形折起,使得平
面、平面均与平面垂直(如图②),连接,,, ,
求点到平面 的距离.
①
②
解:因为平面 平面,平面 平面, ,
平面 ,所以 平面 ,
又因为 平面 ,
所以,又因为 , 所以,,两两垂直
以为原点,,,
所在直线分别为轴、轴、 轴,建立如图所示的空
间直角坐标系,
则,,, ,
所以,, .
设平面的法向量为,则
所以即
令,则,,所以是平面 的一个法向量.
设点到平面的距离为 ,
则,所以点到平面的距离为 .
探究点三 线面距和面面距
例3 如图,在四棱锥中,底面 是边长
为2的正方形, 底面,,, ,
分别是,, 的中点.求:
(1)直线到平面 的距离;
解:因为 平面,四边形 为正方形,
所以,,两两垂直.以点为坐标原点,,,
所在直线分别为,, 轴建立如图所示的空间直角坐标系,
则,,, .
因为,分别为,的中点,所以 ,
又因为 平面, 平面,所以平面 .
因为且,,分别为,的中点,所以且 ,
所以四边形为平行四边形,所以 .
因为 平面, 平面 ,
所以平面 .
因为,, 平面 ,
所以平面平面 .
因为 平面,所以平面,所以直线到平面 的距离等于
点到平面 的距离.
设平面的法向量为 ,
又, ,
则取,可得 ,
又,所以直线到平面 的距离
.
(2)平面与平面 的距离.
解:由(1)知平面平面,所以平面与平面 的距离
.
变式 设正方体 的棱长为2.
(1)求直线到平面 的距离;
解:以为原点,,,所在直线分别为,,
轴,建立如图所示的空间直角坐标系,
则,,,, ,
所以,, ,所以
,即 ,
又 平面, 平面,所以 平面
,所以直线到平面的距离等于点到平面 的距离.
设平面的法向量为 ,
则令,则 ,
又 ,
所以点到平面的距离,即直线到平面 的
距离为 .
(2)求平面与平面 的距离.
解:由(1)知平面,同理可得平面 ,又
,, 平面 ,
所以平面平面,即平面与平面的距离等于点 到平面
的距离.
由(1)知,点到平面的距离 ,
所以平面与平面的距离为 .
[素养小结]
(1)求线面距离可以转化为求直线上任意一点到平面的距离,利用求点到平面
的距离的方法求解即可.
(2)求两个平行平面间的距离可以转化为求点到平面的距离,利用求点到平面
的距离的方法求解即可.
1.四种类型的距离求法
距离类型 求解(转化)方法
点到直线 的距离 已知直线外一点,直线过点,直线的单位方向向量为 ,设
,则点到直线的距离
点到平面 的距离 已知平面 外一点,为平面 上一点,且 的一个法向量为 ,则点
到平面 的距离
线面距离 线面距离可以转化为点面距离求解
面面距离 面面距离可以转化为点面距离求解
2.用空间向量解决立体几何问题可用两种方法
(1)向量法:可具体表示为“设基底——巧运算——译结果”,其中设不共线的三
个向量构成空间的一个基底,并把相关向量用基底表示出来是关键.
(2)坐标法:可具体表示为“建系设点——巧运算——译结果”,其中建立适当的
空间直角坐标系,并确定相关点的坐标是关键.
1.求点到直线的距离,一般先计算所求点与直线上某一点所构成的向量在直线
上的投影向量的长度,再利用勾股定理求解.
例1 (多选题)在空间直角坐标系中,,, ,
则下列结论正确的是( )
BD
A.
B.点到平面 的距离是2
C.异面直线与所成角的余弦值为
D.点到直线的距离是
[解析] 因为,,所以 ,故A错误.
在空间直角坐标系中,结合A与C两点的坐标可知轴与平面 垂直,所以
为平面的一个法向量,则点B到平面的距离是 ,
故B正确.
因为,,所以异面直线与 所成角的余弦值
为,故C错误.
因为,所以,所以点到直线 的距离是
,故D正确.故选 .
2.空间线面、面面距离问题一般转化为点面距离问题解决.若点为平面 外一
点,点为平面 内任意一点,平面 的法向量为,则点到平面 的距离
.
例2 [2024·甘肃张掖高二期中] 如图,正方体
的棱长为2,点为 的中点.
(1)求点到平面 的距离;
解:以为原点,,,所在的直线分别为,,
轴建立如图所示的空间直角坐标系,
则,,, ,
所以, .
设平面的法向量为 ,
则
令,则, ,
所以平面的一个法向量为 .
又 ,
所以点到平面的距离为 .
(2)求到平面 的距离.
解:由(1)可得平面的一个法向量为 ,
因为,,所以 ,
所以 ,
所以,又 平面 ,
所以平面 ,
所以到平面的距离可以转化为点到平面 的距离.
又 ,
所以到平面的距离为 .
