1.1.2 空间向量的数量积运算课件(共40张PPT)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.1.2 空间向量的数量积运算课件(共40张PPT)-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 11:28:48 | ||
图片预览











文档简介
(共40张PPT)
1.1 空间向量及其运算
1.1.2 空间向量的数量积运算
【学习目标】
1.结合立体几何与空间向量的特征,知道投影向量的概念.
2.类比平面向量,能进行空间向量的数量积运算.
3.类比平面向量并借助空间图形,知道空间向量的有关运算律,能运用数
量积解决空间中的垂直、夹角及距离问题.
知识点一 空间向量的夹角
1.概念:如图,已知两个非零向量,,在空间任取一点,作, ,则
叫作向量, 的______,记作______.
夹角
2.夹角的取值范围:与的夹角的取值范围是______,其中当,时,与
方向______;当, 时,与方向______;当,时,与 __________.反
之,若,则,或 ;若,则, .
相同
相反
互相垂直
【诊断分析】 判断正误.(请在括号中打“√”或“×”)
(1)向量与的夹角等于向量与 的夹角.( )
×
[解析] ,表示向量,的夹角,,表示向量, 的夹角,它们之
间的关系为,, .
(2)若向量与的夹角为 ,则直线与所成的角也为 .( )
×
[解析] 若向量与的夹角为 ,则直线与所成的角为 或 .
知识点二 数量积的相关概念及性质
1.概念:已知两个非零向量,,则______________叫作,的数量积,记作 ,即
______________.
特别地,零向量与任意向量的数量积为0.
2.空间向量数量积的性质
(1) ___.
(2), _____.
(3), _____.
0
3.投影向量的概念
作法 图形表示 符号表示
向量 在向量 上的投影向 量 将向量,(直线 平移到同一个平面 内,利用平面上 向量的投影,得到与 向量(直线 的方 向向量)共线的向 量 ______________
向量在直线 上的投影向量
作法 图形表示 符号表示
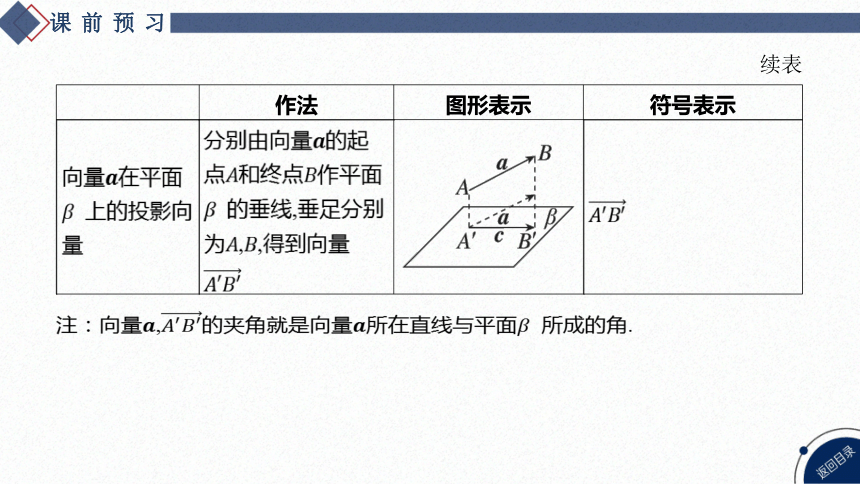
向量 在平面 上的投影向 量 分别由向量 的起 点和终点 作平面 的垂线,垂足分别 为, ,得到向量
注:向量,的夹角就是向量所在直线与平面 所成的角.
续表
4.空间向量数量积的运算律
(1)________, .
(2) _____(交换律).
(3) ___________(分配律).
【诊断分析】 判断正误.(请在括号中打“√”或“×”)
(1)对于向量,,若,则一定有或 .( )
×
[解析] 非零向量,垂直时也有 .
(2)对于非零向量,由,可得 .( )
×
[解析] 向量的数量积运算不满足消去律.
(3)若,则, 是钝角.( )
×
[解析] 若,则,是钝角或, .
(4)已知,是夹角为 的两个单位向量,则向量在向量 上的投影向量
为 .( )
√
[解析] 向量在向量上的投影向量为
探究点一 空间向量的数量积运算
例1 如图所示,在棱长为1的正四面体 中,
,分别是, 的中点,求:
(1) ;
解: .
(2) ;
[答案] .
(3) ;
[答案] .
(4) .
[答案]
变式(1) (多选题)设正方体的棱长为 ,则有( )
AC
A. B.
C. D.
[解析] ,故A正确;
,故B错误;
,故C正确;
,故D错误.故选 .
(2)正四面体的棱长为2,点是的重心,则 ____.
[解析] 点是的重心,,又正四面体 的棱长
为2, .
[素养小结]
(1)空间向量数量积运算的两种方法:
①已知,的模及与 的夹角,直接代入数量积公式计算.
②如果要求的是关于与 的多项式形式的数量积,可以先利用数量积的运算律
将多项式展开,再利用 及数量积公式进行计算.
(2)在几何体中求空间向量数量积的步骤:
①首先将各向量分解成已知模和夹角的向量的组合形式.
②利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
③代入, 求解.
探究点二 利用向量的数量积解决夹角问题
例2 如图所示,在正方体 中.
(1)求与 的夹角;
解:不妨设正方体 的棱长为1,
则 .
,
, .
又,,, ,
即与的夹角为 .
(2)求异面直线与 所成角的大小.
[答案] 由异面直线所成角的范围和(1)得,异面直线与 所成角的大小为
.
变式(1) 已知,是异面直线,,,,, ,
,且,,则与 所成的角是( )
C
A. B. C. D.
[解析] ,
,
又,,, ,又异面直线所成
的角是锐角或直角,与所成的角是 .
(2)已知 平面,且是以 为底边的等腰直角三角形,
和的对角线都分别相互垂直,求异面直线与 所成角
的大小.
解:由题意知和均为正方形,设 ,因为
, ,所以
,
由题意知,, ,
所以,, ,
又因为,所以 ,
所以, .
又因为,,所以, ,又因为异面直线所成的角是
锐角或直角,所以异面直线与所成的角为 .
[素养小结]
(1)求两个空间向量的夹角的两种方法:
①结合图形,平移向量,利用空间向量的夹角定义来求,但要注意向量夹角的范围.
②先求,再利用公式,求,,最后确定, .
(2)用向量法求两直线的夹角:
①取向量:在两直线上分别取方向向量, ;
②运算:求, ;
③结论:设两直线的夹角为 ,则,,进而得到 .
探究点三 利用向量的数量积解决长度问题
例3 已知线段在平面 内,线段 ,线段,且与 所成的角
是 ,如果,,求, 间的距离.
解:由 , 平面 ,得.如图,过点
作 于点 ,
连接,,则 ,
所以
,故 .
变式(1) 如图,在四棱锥中,底面 是边
长为1的正方形,侧棱的长为2,且与, 的夹角
都是 ,若是的中点,则 ( )
A
A. B. C. D.
[解析] 是 的中点,
,又
, ,,, ,
.故选A.
(2)如图,在平行四边形中,, ,沿着它的对角线
将折起,使与所成的角为 ,求此时, 间的距离.
解:因为 ,所以 ,同理, .
因为与所成的角为 ,所以, 或 .
连接因为
所以 .
若 ,则,此时 ;
若, ,则,此时 .
综上,,间的距离为2或 .
[素养小结]
求两点间的距离或线段的长度的步骤:
(1)将两点间的连线(或此线段)用向量表示;
(2)用其他已知夹角和模的向量表示该向量;
(3)利用,计算出 ,即得所求距离或长度.
探究点四 利用空间向量的数量积判断或证明垂直问题
例4 如图,在正方体中,与 相交于点
,求证:
(1) ;
证明:因为 ,
,
所以
,所以,故 .
(2) 平面 .
[答案] ,由题意可知
,
,所以
,所以,所以 .同理可证,
.
又平面, 平面 ,
所以平面 .
变式 如图,在四棱锥中, 平面,四边形 为正方
形,,,分别是,的中点.证明:平面 平面 .
证明:设,,,则,,, .
, ,
,
,, .
又, 平面, 平面 ,
平面,又 平面 ,
平面 平面 .
拓展 写出命题“如果平面内的一条直线和这个平面的一条斜线在这个平面上的
射影垂直,那么它也和这条斜线垂直”的逆命题,判断逆命题的真假,并用向量法证明.
解:命题的逆命题为“如果平面内的一条直线和这个平面的一条斜线垂直,那么
它也和这条斜线在这个平面上的射影垂直”.该命题为真命题.
证明如下:
如图, , ,为一条斜线, .取直
线的方向向量,同时取向量,, .
因为,所以 .
又因为 ,且 ,所以,所以 ,
所以 ,
所以,即 .
1.向量的数量积运算不满足结合律,即.事实上 表
示与平行的向量,而表示与 平行的向量.
2.向量夹角的取值范围为 .当夹角为锐角时,其余弦值为正,当夹角为钝角时,
其余弦值为负.
3.通过学习,我们可以利用向量的数量积解决立体几何中的以下问题:求两直线所
成角的余弦值,求两点之间的距离或线段的长度,证明线面垂直等.
1.求解空间向量的数量积通常先确定两向量的夹角,再结合数量积公式求解.若两
向量夹角不易确定,可结合空间向量的线性运算转化为已知夹角的向量间的数
量积问题再求解.
例1 (多选题)[2024·广东湛江一中高二期中] 如图,在
四棱锥中, 底面,四边形 是
边长为1的菱形,且 , ,则
( )
BD
A. B.
C. D.
[解析] 因为 底面,所以垂直于平面 内的任何一条直线,因
为四边形是边长为1的菱形,且 ,所以和 是等
边三角形.对于A, ,故A错误;
对于B, ,故B正确;
对于C, ,故C错误;
对于D, ,故D正确.故选 .
2.求解空间两点的距离问题,先选择以两点为端点的向量,再将此向量表示为几
个向量和的形式,然后求出这几个已知向量两两之间的夹角以及它们的模,最
后利用公式 求解.
例2 如图所示,已知二面角 的大小为 ,点
,,为垂足,点 ,, 为垂足,且
,,,则线段 的长为( )
B
A.4 B. C. D.
[解析] ,
, ,即线段 的长为
.故选B.
3.证明空间直线垂直问题,一般求出相关直线的一个方向向量,再根据两向量的数
量积为零证明.
例3 如图所示,已知在四面体中,和都是以 为直角顶
点的直角三角形,且, .求证: 平面 .
证明:不妨设,则 .
,
且 ,
,,即 ,
又由题意易知,且, 平面, 平面 ,
平面 .
1.1 空间向量及其运算
1.1.2 空间向量的数量积运算
【学习目标】
1.结合立体几何与空间向量的特征,知道投影向量的概念.
2.类比平面向量,能进行空间向量的数量积运算.
3.类比平面向量并借助空间图形,知道空间向量的有关运算律,能运用数
量积解决空间中的垂直、夹角及距离问题.
知识点一 空间向量的夹角
1.概念:如图,已知两个非零向量,,在空间任取一点,作, ,则
叫作向量, 的______,记作______.
夹角
2.夹角的取值范围:与的夹角的取值范围是______,其中当,时,与
方向______;当, 时,与方向______;当,时,与 __________.反
之,若,则,或 ;若,则, .
相同
相反
互相垂直
【诊断分析】 判断正误.(请在括号中打“√”或“×”)
(1)向量与的夹角等于向量与 的夹角.( )
×
[解析] ,表示向量,的夹角,,表示向量, 的夹角,它们之
间的关系为,, .
(2)若向量与的夹角为 ,则直线与所成的角也为 .( )
×
[解析] 若向量与的夹角为 ,则直线与所成的角为 或 .
知识点二 数量积的相关概念及性质
1.概念:已知两个非零向量,,则______________叫作,的数量积,记作 ,即
______________.
特别地,零向量与任意向量的数量积为0.
2.空间向量数量积的性质
(1) ___.
(2), _____.
(3), _____.
0
3.投影向量的概念
作法 图形表示 符号表示
向量 在向量 上的投影向 量 将向量,(直线 平移到同一个平面 内,利用平面上 向量的投影,得到与 向量(直线 的方 向向量)共线的向 量 ______________
向量在直线 上的投影向量
作法 图形表示 符号表示
向量 在平面 上的投影向 量 分别由向量 的起 点和终点 作平面 的垂线,垂足分别 为, ,得到向量
注:向量,的夹角就是向量所在直线与平面 所成的角.
续表
4.空间向量数量积的运算律
(1)________, .
(2) _____(交换律).
(3) ___________(分配律).
【诊断分析】 判断正误.(请在括号中打“√”或“×”)
(1)对于向量,,若,则一定有或 .( )
×
[解析] 非零向量,垂直时也有 .
(2)对于非零向量,由,可得 .( )
×
[解析] 向量的数量积运算不满足消去律.
(3)若,则, 是钝角.( )
×
[解析] 若,则,是钝角或, .
(4)已知,是夹角为 的两个单位向量,则向量在向量 上的投影向量
为 .( )
√
[解析] 向量在向量上的投影向量为
探究点一 空间向量的数量积运算
例1 如图所示,在棱长为1的正四面体 中,
,分别是, 的中点,求:
(1) ;
解: .
(2) ;
[答案] .
(3) ;
[答案] .
(4) .
[答案]
变式(1) (多选题)设正方体的棱长为 ,则有( )
AC
A. B.
C. D.
[解析] ,故A正确;
,故B错误;
,故C正确;
,故D错误.故选 .
(2)正四面体的棱长为2,点是的重心,则 ____.
[解析] 点是的重心,,又正四面体 的棱长
为2, .
[素养小结]
(1)空间向量数量积运算的两种方法:
①已知,的模及与 的夹角,直接代入数量积公式计算.
②如果要求的是关于与 的多项式形式的数量积,可以先利用数量积的运算律
将多项式展开,再利用 及数量积公式进行计算.
(2)在几何体中求空间向量数量积的步骤:
①首先将各向量分解成已知模和夹角的向量的组合形式.
②利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
③代入, 求解.
探究点二 利用向量的数量积解决夹角问题
例2 如图所示,在正方体 中.
(1)求与 的夹角;
解:不妨设正方体 的棱长为1,
则 .
,
, .
又,,, ,
即与的夹角为 .
(2)求异面直线与 所成角的大小.
[答案] 由异面直线所成角的范围和(1)得,异面直线与 所成角的大小为
.
变式(1) 已知,是异面直线,,,,, ,
,且,,则与 所成的角是( )
C
A. B. C. D.
[解析] ,
,
又,,, ,又异面直线所成
的角是锐角或直角,与所成的角是 .
(2)已知 平面,且是以 为底边的等腰直角三角形,
和的对角线都分别相互垂直,求异面直线与 所成角
的大小.
解:由题意知和均为正方形,设 ,因为
, ,所以
,
由题意知,, ,
所以,, ,
又因为,所以 ,
所以, .
又因为,,所以, ,又因为异面直线所成的角是
锐角或直角,所以异面直线与所成的角为 .
[素养小结]
(1)求两个空间向量的夹角的两种方法:
①结合图形,平移向量,利用空间向量的夹角定义来求,但要注意向量夹角的范围.
②先求,再利用公式,求,,最后确定, .
(2)用向量法求两直线的夹角:
①取向量:在两直线上分别取方向向量, ;
②运算:求, ;
③结论:设两直线的夹角为 ,则,,进而得到 .
探究点三 利用向量的数量积解决长度问题
例3 已知线段在平面 内,线段 ,线段,且与 所成的角
是 ,如果,,求, 间的距离.
解:由 , 平面 ,得.如图,过点
作 于点 ,
连接,,则 ,
所以
,故 .
变式(1) 如图,在四棱锥中,底面 是边
长为1的正方形,侧棱的长为2,且与, 的夹角
都是 ,若是的中点,则 ( )
A
A. B. C. D.
[解析] 是 的中点,
,又
, ,,, ,
.故选A.
(2)如图,在平行四边形中,, ,沿着它的对角线
将折起,使与所成的角为 ,求此时, 间的距离.
解:因为 ,所以 ,同理, .
因为与所成的角为 ,所以, 或 .
连接因为
所以 .
若 ,则,此时 ;
若, ,则,此时 .
综上,,间的距离为2或 .
[素养小结]
求两点间的距离或线段的长度的步骤:
(1)将两点间的连线(或此线段)用向量表示;
(2)用其他已知夹角和模的向量表示该向量;
(3)利用,计算出 ,即得所求距离或长度.
探究点四 利用空间向量的数量积判断或证明垂直问题
例4 如图,在正方体中,与 相交于点
,求证:
(1) ;
证明:因为 ,
,
所以
,所以,故 .
(2) 平面 .
[答案] ,由题意可知
,
,所以
,所以,所以 .同理可证,
.
又平面, 平面 ,
所以平面 .
变式 如图,在四棱锥中, 平面,四边形 为正方
形,,,分别是,的中点.证明:平面 平面 .
证明:设,,,则,,, .
, ,
,
,, .
又, 平面, 平面 ,
平面,又 平面 ,
平面 平面 .
拓展 写出命题“如果平面内的一条直线和这个平面的一条斜线在这个平面上的
射影垂直,那么它也和这条斜线垂直”的逆命题,判断逆命题的真假,并用向量法证明.
解:命题的逆命题为“如果平面内的一条直线和这个平面的一条斜线垂直,那么
它也和这条斜线在这个平面上的射影垂直”.该命题为真命题.
证明如下:
如图, , ,为一条斜线, .取直
线的方向向量,同时取向量,, .
因为,所以 .
又因为 ,且 ,所以,所以 ,
所以 ,
所以,即 .
1.向量的数量积运算不满足结合律,即.事实上 表
示与平行的向量,而表示与 平行的向量.
2.向量夹角的取值范围为 .当夹角为锐角时,其余弦值为正,当夹角为钝角时,
其余弦值为负.
3.通过学习,我们可以利用向量的数量积解决立体几何中的以下问题:求两直线所
成角的余弦值,求两点之间的距离或线段的长度,证明线面垂直等.
1.求解空间向量的数量积通常先确定两向量的夹角,再结合数量积公式求解.若两
向量夹角不易确定,可结合空间向量的线性运算转化为已知夹角的向量间的数
量积问题再求解.
例1 (多选题)[2024·广东湛江一中高二期中] 如图,在
四棱锥中, 底面,四边形 是
边长为1的菱形,且 , ,则
( )
BD
A. B.
C. D.
[解析] 因为 底面,所以垂直于平面 内的任何一条直线,因
为四边形是边长为1的菱形,且 ,所以和 是等
边三角形.对于A, ,故A错误;
对于B, ,故B正确;
对于C, ,故C错误;
对于D, ,故D正确.故选 .
2.求解空间两点的距离问题,先选择以两点为端点的向量,再将此向量表示为几
个向量和的形式,然后求出这几个已知向量两两之间的夹角以及它们的模,最
后利用公式 求解.
例2 如图所示,已知二面角 的大小为 ,点
,,为垂足,点 ,, 为垂足,且
,,,则线段 的长为( )
B
A.4 B. C. D.
[解析] ,
, ,即线段 的长为
.故选B.
3.证明空间直线垂直问题,一般求出相关直线的一个方向向量,再根据两向量的数
量积为零证明.
例3 如图所示,已知在四面体中,和都是以 为直角顶
点的直角三角形,且, .求证: 平面 .
证明:不妨设,则 .
,
且 ,
,,即 ,
又由题意易知,且, 平面, 平面 ,
平面 .
