山东省青岛市城阳七中2015-2016学年八年级(上)期中数学试卷【解析版】
文档属性
| 名称 | 山东省青岛市城阳七中2015-2016学年八年级(上)期中数学试卷【解析版】 |  | |
| 格式 | zip | ||
| 文件大小 | 523.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
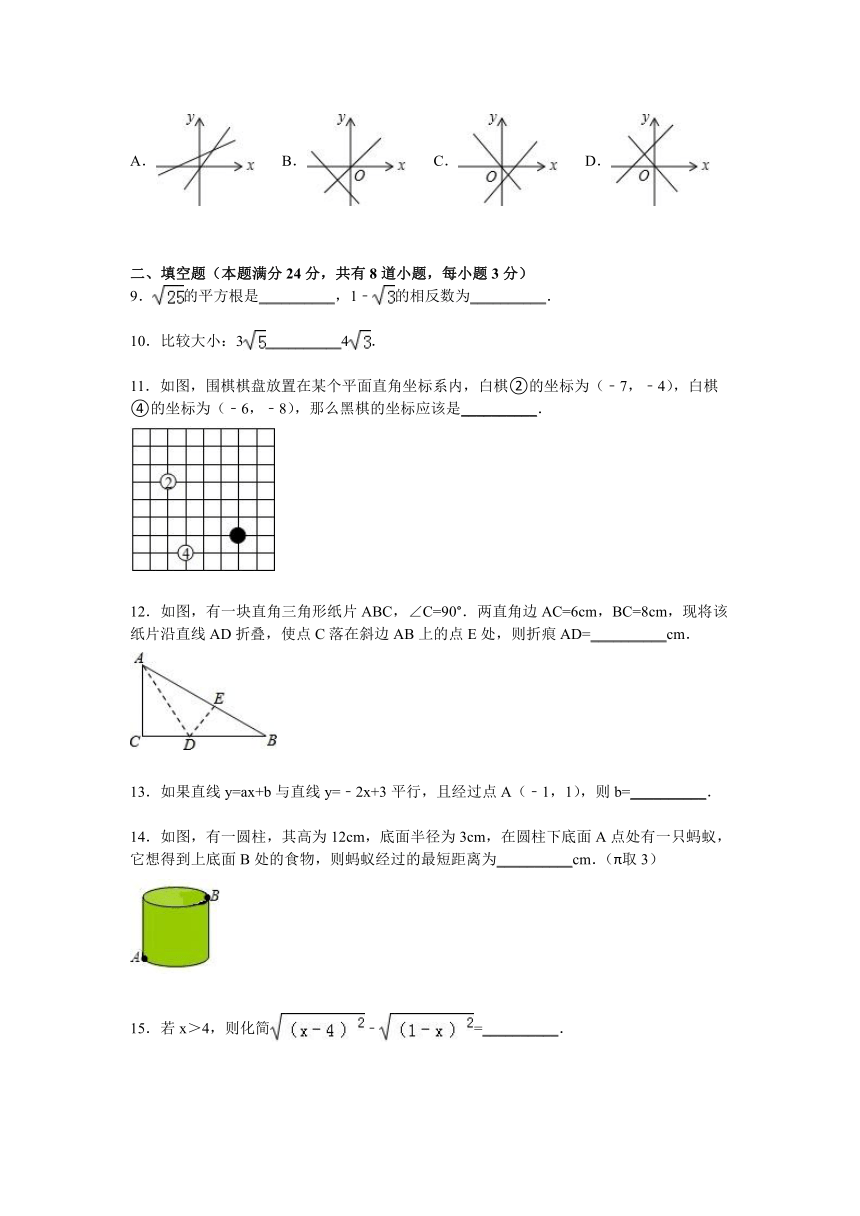
| 更新时间 | 2016-02-20 11:12:57 | ||
图片预览




文档简介
2015-2016学年山东省青岛市城阳七中八年级(上)期中数学试卷
一、选择题(本题满分24分,共有8道小题,每小题3分)
1.在下列各数0.246,6π,﹣24.1010010001…(两个1之间依次多1个0),0,,,中,无理数的个数是( )
A.1 B.2 C.3 D.4
2.下列运算中,错误的有( )
①=;②=±4;③==﹣2;④=+=.
A.1个 B.2个 C.3个 D.4个
3.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
4.估计﹣1的值在哪两个整数之间( )
A.1与2 B.2与3 C.3与4 D.4与5
5.若点A(a+3,a+1)在直角坐标系的y轴上,则点A的坐标是( )
A.(0,﹣2) B.(2,0) C.(4,0) D.(0,﹣4)
6.若函数y=(m﹣1)x|m|﹣5是一次函数,则m的值为( )
A.±1 B.﹣1 C.1 D.2
7.有一个数值转换器,流程如图,当输入的x为81时,输出的y是( )
( http: / / www.21cnjy.com )
A. B.3 C.9 D.2
8.正比例函数y=kx(k≠0)和一次函数y=x﹣k在同一个直角坐标系内的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二、填空题(本题满分24分,共有8道小题,每小题3分)
9.的平方根是__________,1﹣的相反数为__________.
10.比较大小:3__________4.
11.如图,围棋棋盘放置在某个平面直角坐 ( http: / / www.21cnjy.com )标系内,白棋②的坐标为(﹣7,﹣4),白棋④的坐标为(﹣6,﹣8),那么黑棋的坐标应该是__________.
( http: / / www.21cnjy.com )
12.如图,有一块直角三角形纸片ABC,∠ ( http: / / www.21cnjy.com )C=90°.两直角边AC=6cm,BC=8cm,现将该纸片沿直线AD折叠,使点C落在斜边AB上的点E处,则折痕AD=__________cm.
( http: / / www.21cnjy.com )
13.如果直线y=ax+b与直线y=﹣2x+3平行,且经过点A(﹣1,1),则b=__________.
14.如图,有一圆柱,其高为12cm,底面 ( http: / / www.21cnjy.com )半径为3cm,在圆柱下底面A点处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为__________cm.(π取3)
( http: / / www.21cnjy.com )
15.若x>4,则化简﹣=__________.
16.如图,以等腰三角形A ( http: / / www.21cnjy.com )OB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第n个等腰直角三角形的面积Sn=__________.
( http: / / www.21cnjy.com )
三、解答题(本题满分64分)
17.(24分)化简
(1)
(2)3﹣5
(3)(2﹣1)2
(4)
(5)
(6)2﹣.
18.已知点A(﹣2,﹣1),B(3,1),C(1,4).
(1)在直角坐标系中描出点A、B、C,画出△ABC.
(2)求出△ABC的面积.
(3)作出△ABC在坐标系中关于y轴对称的△A1B1C1.
( http: / / www.21cnjy.com )
19.如图所示,有一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积.
( http: / / www.21cnjy.com )
20.某日通过高速公路收费站的汽车中, ( http: / / www.21cnjy.com )共有3000辆次缴了通行费,其中大车每辆次缴费20元,小车每辆次缴费10元.设这一天小车缴通行费的辆次为x,总的通行费收入为y元.
(1)试写出y关于x的函数关系式;
(2)若小车缴通行的辆次为1200,这天的通行费收入是多少元?
21.如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距__________千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是__________小时.
(3)B出发后__________小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?
( http: / / www.21cnjy.com )
22.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+=(1+)2.善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为整数),则有a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=,用含m、n的式子分别表示a、b,得:a=__________,b=__________;
(2)利用所探索的结论,找一组正整数a、b、m、n填空:__________+__________=(__________+__________)2;
(3)若a+4=,且a、m、n均为正整数,求a的值?
2015-2016学年山东省青岛市城阳七中八年级(上)期中数学试卷
一、选择题(本题满分24分,共有8道小题,每小题3分)
1.在下列各数0.246,6π,﹣24.1010010001…(两个1之间依次多1个0),0,,,中,无理数的个数是( )
A.1 B.2 C.3 D.4
【考点】无理数.
【分析】无理数就是无限不循环小数. ( http: / / www.21cnjy.com )理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】解:6π,﹣24.1010010001…(两个1之间依次多1个0),是无理数,
故选:C.
【点评】此题主要考查了无理数的定义 ( http: / / www.21cnjy.com ),其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
2.下列运算中,错误的有( )
①=;②=±4;③==﹣2;④=+=.
A.1个 B.2个 C.3个 D.4个
【考点】算术平方根.
【分析】根据二次根式的性质,可得答案.
【解答】解;①=,故①错误;
②=4,故②错误;
③负数没有平方根,故③错误;
④==,故④错误;
故选:D.
【点评】本题考查了算术平方根,注意负数没有平方根.
3.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【考点】勾股定理的逆定理.
【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
【解答】解:A、72+242=252,152+202≠242,222+202≠252,故A不正确;
B、72+242=252,152+202≠242,故B不正确;
C、72+242=252,152+202=252,故C正确;
D、72+202≠252,242+152≠252,故D不正确.
故选:C.
【点评】本题考查勾股定理的逆定理的应用.判断 ( http: / / www.21cnjy.com )三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.勾股定理的逆定理:若三角形三边满足a2+b2=c2,那么这个三角形是直角三角形.
4.估计﹣1的值在哪两个整数之间( )
A.1与2 B.2与3 C.3与4 D.4与5
【考点】估算无理数的大小.
【分析】首先根据4<5<9,估算2<<3,确定﹣1的取值范围.
【解答】解:∵4<5<9,
∴2<<3,
∴1<﹣1<2,
故选A.
【点评】本题主要考查了估算无理数的大小,首先用算术平方根估算的取值范围是解答此题的关键.
5.若点A(a+3,a+1)在直角坐标系的y轴上,则点A的坐标是( )
A.(0,﹣2) B.(2,0) C.(4,0) D.(0,﹣4)
【考点】点的坐标.
【分析】根据y轴上点的横坐标为0列式求出a,再求解即可.
【解答】解:∵点A(a+3,a+1)在y轴上,
∴a+3=0,
解得a=﹣3,
所以,a+1=﹣3+1=﹣2,
所以,点A的坐标为(0,﹣2).
故选A.
【点评】本题考查了点的坐标,是基础题,熟记y轴上点的横坐标为0是解题的关键.
6.若函数y=(m﹣1)x|m|﹣5是一次函数,则m的值为( )
A.±1 B.﹣1 C.1 D.2
【考点】一次函数的定义.
【分析】根据一次函数的定义列式计算即可得解.
【解答】解:根据题意得,|m|=1且m﹣1≠0,
解得m=±1且m≠1,
所以,m=﹣1.
故选B.
【点评】本题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
7.有一个数值转换器,流程如图,当输入的x为81时,输出的y是( )
( http: / / www.21cnjy.com )
A. B.3 C.9 D.2
【考点】算术平方根.
【专题】图表型.
【分析】根据开方运算,可得算术平方根.
【解答】解:=9,=3,
y=,
故选:A.
【点评】本题考查了算术平方根,求算术平方根,直到不能开方为止.
8.正比例函数y=kx(k≠0)和一次函数y=x﹣k在同一个直角坐标系内的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【考点】一次函数的图象;正比例函数的图象.
【分析】根据正比例函数和一次函数的图象性质并结合其系数作答.
【解答】解:当k>0时,正比例函数图象经过1,3象限,一次函数图象经过1,3,2象限,
当k<0时,正比例函数图象经过2,4象限,一次函数图象经过1,3,4象限.
故选A.
【点评】本题主要考查了一次函数的图象性质和正比例函数的图象性质,关键是由k的取值确定函数所在的象限.
二、填空题(本题满分24分,共有8道小题,每小题3分)
9.的平方根是,1﹣的相反数为﹣1.
【考点】实数的性质;平方根;算术平方根.
【分析】根据开方运算,可得一个数的平方根;根据只有符号不同的两个数互为相反数,可得答案.
【解答】解:=5,5的平方根是,
1﹣的相反数是﹣1,
故答案为:,﹣1.
【点评】本题考查了实数的性质,在一个数的前面加上负号就是这个数的相反数,注意先求算术平方根再求平方根.
10.比较大小:3<4.
【考点】实数大小比较.
【专题】推理填空题;实数.
【分析】首先分别求出3、4的平方的值各是多少;然后根据实数大小比较的方法,判断出3、4的平方的大小关系,即可判断出3、4的大小关系.
【解答】解:(1)=45,(4)2=48,
∵45<48,
∴3<4.
故答案为:<.
【点评】(1)此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
(2)解答此题的关键是比较出3、4这两个数的平方的大小关系.
11.如图,围棋棋盘放置在 ( http: / / www.21cnjy.com )某个平面直角坐标系内,白棋②的坐标为(﹣7,﹣4),白棋④的坐标为(﹣6,﹣8),那么黑棋的坐标应该是(﹣3,﹣7).
( http: / / www.21cnjy.com )
【考点】坐标确定位置.
【分析】根据点的坐标向右平移加,向上平移加,可得答案.
【解答】解:由(﹣6,﹣8)的位置向右平移3个单位,向上平移1个单位,得
﹣6+3=﹣3,﹣8+1=﹣7,
故答案为:(﹣3,﹣7).
【点评】本题考查了坐标确定位置,利用点的坐标向右平移加,向上平移加是解题关键.
12.如图,有一块直角三角形纸片ABC,∠C=90°.两直角边AC=6cm,BC=8cm,现将该纸片沿直线AD折叠,使点C落在斜边AB上的点E处,则折痕AD=3cm.
( http: / / www.21cnjy.com )
【考点】翻折变换(折叠问题).
【分析】先根据勾股定理求得AB的长,再根据折叠的性质求得AE,BE的长,从而利用勾股定理可求得CD的长,然后根据勾股定理即可求得AD.
【解答】解:∵AC=6cm,BC=8cm,∠C=90°
∴AB=10cm,
∵AE=6cm(折叠的性质),
∴BE=4cm,
设CD=x,
则在Rt△DEB中,
42+x2=(8﹣x)2,
∴x=3cm.
∴CD=3cm,
在Rt△ACD中,AD==3cm.
故答案为3.
【点评】本题考查了翻折变换的性质,勾股定理的应用,熟记性质并表示出Rt△DEB的三边,然后利用勾股定理列出方程是解题的关键.
13.如果直线y=ax+b与直线y=﹣2x+3平行,且经过点A(﹣1,1),则b=﹣1.
【考点】两条直线相交或平行问题.
【分析】相互平行的两条直线的一次项系数相等,故此a=﹣2,将a=﹣2,x=﹣1,y=1代入y=ax+b可求得b的值.
【解答】解:∵直线y=ax+b与直线y=﹣2x+3平行,
∴a=﹣2.
∴直线y=ax+b的解析式为y=﹣2x+b.
将x=﹣1,y=1代入得:﹣2×(﹣1)+b=1.
解得:b=﹣1.
故答案为:﹣1.
【点评】本题主要考查的是两条直线平行问题,明确相互平行的两条直线的一次项系数相等是解题的关键.
14.如图,有一圆柱,其 ( http: / / www.21cnjy.com )高为12cm,底面半径为3cm,在圆柱下底面A点处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为15cm.(π取3)
( http: / / www.21cnjy.com )
【考点】平面展开-最短路径问题.
【分析】本题应先把圆柱展开即得其平面展 ( http: / / www.21cnjy.com )开图,则A,B所在的长方形的长为圆柱的高12cm,宽为底面圆周长的一半为πr,蚂蚁经过的最短距离为连接A,B的线段长,由勾股定理求得AB的长.
【解答】解:圆柱展开图为长方形,
则A,B所在的长方形的长为圆柱的高12cm,宽为底面圆周长的一半为πrcm,
蚂蚁经过的最短距离为连接A,B的线段长,
由勾股定理得AB====15cm.
故蚂蚁经过的最短距离为15cm.(π取3)
( http: / / www.21cnjy.com )
【点评】解答本题的关键是计算出圆柱展开后所得长方形长和宽的值,然后用勾股定理计算即可.
15.若x>4,则化简﹣=﹣3.
【考点】二次根式的性质与化简.
【专题】计算题;二次根式.
【分析】根据x的范围判断出x﹣4与1﹣x的正负,利用二次根式性质化简,计算即可得到结果.
【解答】解:∵x>4,
∴x﹣4>0,1﹣x<0,
则原式=|x﹣4|﹣|1﹣x|=x﹣4+1﹣x=﹣3.
故答案为:﹣3.
【点评】此题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.
16.如图,以等腰三角形AOB的斜边为 ( http: / / www.21cnjy.com )直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第n个等腰直角三角形的面积Sn=2n﹣2.
( http: / / www.21cnjy.com )
【考点】等腰直角三角形.
【专题】压轴题;规律型.
【分析】本题要先根据已知的条件求出S1、S2的值,然后通过这两个面积的求解过程得出一般化规律,进而可得出Sn的表达式.
【解答】解:根据直角三角形的面积公式,得S1==2﹣1;
根据勾股定理,得:AB=,则S2=1=20;
A1B=2,则S3=21,
依此类推,发现:Sn=2n﹣2.
【点评】本题要先从简单的例子入手得出一般化的结论,然后根据得出的规律去求特定的值.
三、解答题(本题满分64分)
17.(24分)化简
(1)
(2)3﹣5
(3)(2﹣1)2
(4)
(5)
(6)2﹣.
【考点】二次根式的混合运算.
【专题】计算题.
【分析】(1)利用二次根式的性质化简;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)利用完全平方公式计算;
(4)利用平方差公式计算;
(5)先把各二次根式化为最简二次根式,然后合并即可;
(6)先把化简,然后合并后进行二次根式的除法运算,再进行减法运算.
【解答】解:(1)原式==;
(2)原式=6﹣20=﹣14;
(3)原式=12﹣4+1=13﹣4;
(4)原式=(2)2﹣1=20﹣1=19;
(5)原式=4+﹣=;
(6)原式=2﹣=2﹣3=﹣1.
【点评】本题考查了二次根式的计算: ( http: / / www.21cnjy.com )先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.
18.已知点A(﹣2,﹣1),B(3,1),C(1,4).
(1)在直角坐标系中描出点A、B、C,画出△ABC.
(2)求出△ABC的面积.
(3)作出△ABC在坐标系中关于y轴对称的△A1B1C1.
( http: / / www.21cnjy.com )
【考点】作图-轴对称变换.
【分析】(1)利用已知点在坐标系中得出各点位置即可;
(2)利用△ABC所在矩形面积减去周围三角形面积进而得出答案;
(3)利用关于y轴对称点的性质得出各对应点位置即可得出答案.
【解答】解:(1)如图所示:△ABC即为所求;
(2)S△ABC=5×5﹣×2×3﹣×3×5﹣×2×5=9.5;
(3)如图所示:△A1B1C1,即为所求.
( http: / / www.21cnjy.com )
【点评】此题主要考查了轴对称变换以及三角形面积求法,根据题意得出对应点位置是解题关键.
19.如图所示,有一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积.
( http: / / www.21cnjy.com )
【考点】勾股定理的逆定理;勾股定理.
【分析】连接AC,先利用勾股定理求出AC ( http: / / www.21cnjy.com ),再根据勾股定理的逆定理判定△ABC是直角三角形,那么△ABC的面积减去△ACD的面积就是所求的面积.
【解答】解:如图,连接AC.
在△ACD中,∵AD=4米,CD=3米,∠ADC=90°,
∴AC=5米,
又∵AC2+BC2=52+122=132=AB2,
∴△ABC是直角三角形,
∴这块地的面积=△ABC的面积﹣△ACD的面积=×5×12﹣×3×4=24(平方米).
( http: / / www.21cnjy.com )
【点评】本题考查了勾股定理、勾股定理的逆定理的应用,得到△ABC是直角三角形是解题的关键.同时考查了直角三角形的面积公式.
20.某日通过高速公路收费站的汽车中 ( http: / / www.21cnjy.com ),共有3000辆次缴了通行费,其中大车每辆次缴费20元,小车每辆次缴费10元.设这一天小车缴通行费的辆次为x,总的通行费收入为y元.
(1)试写出y关于x的函数关系式;
(2)若小车缴通行的辆次为1200,这天的通行费收入是多少元?
【考点】一次函数的应用.
【分析】(1)小车有x辆,则大车有(3000﹣x)辆,根据:总通行费=小车通行费+大车通行费,列出函数关系式;
(2)把x=1200代入(1)中的函数关系式即可.
【解答】解:(1)依题意,得y=10x+20(3000﹣x)=﹣10x+60000;
(2)当x=1200时,y=﹣10×1200+60000=48000元.
答:这天的通行费收入是48000元.
【点评】本题考查了一次函数的应用.关键是根据总通行费=小车通行费+大车通行费,列出函数关系式.
21.如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距10千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是1小时.
(3)B出发后3小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?
( http: / / www.21cnjy.com )
【考点】一次函数的应用.
【专题】行程问题.
【分析】(1)根据函数图象可以直接看出B出发时与A相距的路程;
(2)根据函数图象可以得到走了一段路后,自行车发生故障进行修理所用的时间;
(3)根据函数图象可以直接得到B出发后多长时间与A相遇;
(4)根据直线lA经过点(0,10),(3,25)可以求得它的解析式;
(5)根据函数图象可以求得lB的解析式与直线lA联立方程组即可求得相遇的时间.
【解答】解:(1)根据函数图象可知,B出发时与A相距10千米,
故答案为:10;
(2)根据函数图象可知,走了一段路后,自行车发生故障进行修理,所用的时间是1.5﹣0.5=1小时,
故答案为:1;
(3)根据图象可知B出发后3小时时与A相遇;
(4)根据函数图象可知直线lA经过点(0,10),(3,25).
设直线lA的解析式为:S=kt+b,则
解得,k=5,b=10
即A行走的路程S与时间t的函数关系式是:S=5t+10;
(5)设直线lB的解析式为:S=kt,
∵点(0.5,7.5)在直线lB上,
∴7.5=k×0.5
得k=15
∴S=15t.
∴
解得S=15,t=1.
故若B的自行车不发生故障,保持出发时的速度前进,1小时时与A相遇.
【点评】本题考查一次函数的应用,解体的关键是利用数形结合的思想对图象进行分析,找出所求问题需要的条件.
22.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+=(1+)2.善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为整数),则有a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=,用含m、n的式子分别表示a、b,得:a=m2+3n2,b=2mn;
(2)利用所探索的结论,找一组正整数a、b、m、n填空:4+2=(1+1)2;
(3)若a+4=,且a、m、n均为正整数,求a的值?
【考点】二次根式的混合运算.
【分析】(1)根据完全平方公式运算法则,即可得出a、b的表达式;
(2)首先确定好m、n的正整数值,然后根据(1)的结论即可求出a、b的值;
(3)根据题意,4=2mn,首先确定m、n的值,通过分析m=2,n=1或者m=1,n=2,然后即可确定好a的值.
【解答】解:(1)∵a+b=,
∴a+b=m2+3n2+2mn,
∴a=m2+3n2,b=2mn.
故答案为:m2+3n2,2mn.
(2)设m=1,n=1,
∴a=m2+3n2=4,b=2mn=2.
故答案为4、2、1、1.
(3)由题意,得:
a=m2+3n2,b=2mn
∵4=2mn,且m、n为正整数,
∴m=2,n=1或者m=1,n=2,
∴a=22+3×12=7,或a=12+3×22=13.
【点评】本题主要考查二次根式的混合运算,完全平方公式,解题的关键在于熟练运算完全平方公式和二次根式的运算法则.
一、选择题(本题满分24分,共有8道小题,每小题3分)
1.在下列各数0.246,6π,﹣24.1010010001…(两个1之间依次多1个0),0,,,中,无理数的个数是( )
A.1 B.2 C.3 D.4
2.下列运算中,错误的有( )
①=;②=±4;③==﹣2;④=+=.
A.1个 B.2个 C.3个 D.4个
3.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
4.估计﹣1的值在哪两个整数之间( )
A.1与2 B.2与3 C.3与4 D.4与5
5.若点A(a+3,a+1)在直角坐标系的y轴上,则点A的坐标是( )
A.(0,﹣2) B.(2,0) C.(4,0) D.(0,﹣4)
6.若函数y=(m﹣1)x|m|﹣5是一次函数,则m的值为( )
A.±1 B.﹣1 C.1 D.2
7.有一个数值转换器,流程如图,当输入的x为81时,输出的y是( )
( http: / / www.21cnjy.com )
A. B.3 C.9 D.2
8.正比例函数y=kx(k≠0)和一次函数y=x﹣k在同一个直角坐标系内的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
二、填空题(本题满分24分,共有8道小题,每小题3分)
9.的平方根是__________,1﹣的相反数为__________.
10.比较大小:3__________4.
11.如图,围棋棋盘放置在某个平面直角坐 ( http: / / www.21cnjy.com )标系内,白棋②的坐标为(﹣7,﹣4),白棋④的坐标为(﹣6,﹣8),那么黑棋的坐标应该是__________.
( http: / / www.21cnjy.com )
12.如图,有一块直角三角形纸片ABC,∠ ( http: / / www.21cnjy.com )C=90°.两直角边AC=6cm,BC=8cm,现将该纸片沿直线AD折叠,使点C落在斜边AB上的点E处,则折痕AD=__________cm.
( http: / / www.21cnjy.com )
13.如果直线y=ax+b与直线y=﹣2x+3平行,且经过点A(﹣1,1),则b=__________.
14.如图,有一圆柱,其高为12cm,底面 ( http: / / www.21cnjy.com )半径为3cm,在圆柱下底面A点处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为__________cm.(π取3)
( http: / / www.21cnjy.com )
15.若x>4,则化简﹣=__________.
16.如图,以等腰三角形A ( http: / / www.21cnjy.com )OB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第n个等腰直角三角形的面积Sn=__________.
( http: / / www.21cnjy.com )
三、解答题(本题满分64分)
17.(24分)化简
(1)
(2)3﹣5
(3)(2﹣1)2
(4)
(5)
(6)2﹣.
18.已知点A(﹣2,﹣1),B(3,1),C(1,4).
(1)在直角坐标系中描出点A、B、C,画出△ABC.
(2)求出△ABC的面积.
(3)作出△ABC在坐标系中关于y轴对称的△A1B1C1.
( http: / / www.21cnjy.com )
19.如图所示,有一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积.
( http: / / www.21cnjy.com )
20.某日通过高速公路收费站的汽车中, ( http: / / www.21cnjy.com )共有3000辆次缴了通行费,其中大车每辆次缴费20元,小车每辆次缴费10元.设这一天小车缴通行费的辆次为x,总的通行费收入为y元.
(1)试写出y关于x的函数关系式;
(2)若小车缴通行的辆次为1200,这天的通行费收入是多少元?
21.如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距__________千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是__________小时.
(3)B出发后__________小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?
( http: / / www.21cnjy.com )
22.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+=(1+)2.善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为整数),则有a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=,用含m、n的式子分别表示a、b,得:a=__________,b=__________;
(2)利用所探索的结论,找一组正整数a、b、m、n填空:__________+__________=(__________+__________)2;
(3)若a+4=,且a、m、n均为正整数,求a的值?
2015-2016学年山东省青岛市城阳七中八年级(上)期中数学试卷
一、选择题(本题满分24分,共有8道小题,每小题3分)
1.在下列各数0.246,6π,﹣24.1010010001…(两个1之间依次多1个0),0,,,中,无理数的个数是( )
A.1 B.2 C.3 D.4
【考点】无理数.
【分析】无理数就是无限不循环小数. ( http: / / www.21cnjy.com )理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】解:6π,﹣24.1010010001…(两个1之间依次多1个0),是无理数,
故选:C.
【点评】此题主要考查了无理数的定义 ( http: / / www.21cnjy.com ),其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
2.下列运算中,错误的有( )
①=;②=±4;③==﹣2;④=+=.
A.1个 B.2个 C.3个 D.4个
【考点】算术平方根.
【分析】根据二次根式的性质,可得答案.
【解答】解;①=,故①错误;
②=4,故②错误;
③负数没有平方根,故③错误;
④==,故④错误;
故选:D.
【点评】本题考查了算术平方根,注意负数没有平方根.
3.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【考点】勾股定理的逆定理.
【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
【解答】解:A、72+242=252,152+202≠242,222+202≠252,故A不正确;
B、72+242=252,152+202≠242,故B不正确;
C、72+242=252,152+202=252,故C正确;
D、72+202≠252,242+152≠252,故D不正确.
故选:C.
【点评】本题考查勾股定理的逆定理的应用.判断 ( http: / / www.21cnjy.com )三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.勾股定理的逆定理:若三角形三边满足a2+b2=c2,那么这个三角形是直角三角形.
4.估计﹣1的值在哪两个整数之间( )
A.1与2 B.2与3 C.3与4 D.4与5
【考点】估算无理数的大小.
【分析】首先根据4<5<9,估算2<<3,确定﹣1的取值范围.
【解答】解:∵4<5<9,
∴2<<3,
∴1<﹣1<2,
故选A.
【点评】本题主要考查了估算无理数的大小,首先用算术平方根估算的取值范围是解答此题的关键.
5.若点A(a+3,a+1)在直角坐标系的y轴上,则点A的坐标是( )
A.(0,﹣2) B.(2,0) C.(4,0) D.(0,﹣4)
【考点】点的坐标.
【分析】根据y轴上点的横坐标为0列式求出a,再求解即可.
【解答】解:∵点A(a+3,a+1)在y轴上,
∴a+3=0,
解得a=﹣3,
所以,a+1=﹣3+1=﹣2,
所以,点A的坐标为(0,﹣2).
故选A.
【点评】本题考查了点的坐标,是基础题,熟记y轴上点的横坐标为0是解题的关键.
6.若函数y=(m﹣1)x|m|﹣5是一次函数,则m的值为( )
A.±1 B.﹣1 C.1 D.2
【考点】一次函数的定义.
【分析】根据一次函数的定义列式计算即可得解.
【解答】解:根据题意得,|m|=1且m﹣1≠0,
解得m=±1且m≠1,
所以,m=﹣1.
故选B.
【点评】本题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
7.有一个数值转换器,流程如图,当输入的x为81时,输出的y是( )
( http: / / www.21cnjy.com )
A. B.3 C.9 D.2
【考点】算术平方根.
【专题】图表型.
【分析】根据开方运算,可得算术平方根.
【解答】解:=9,=3,
y=,
故选:A.
【点评】本题考查了算术平方根,求算术平方根,直到不能开方为止.
8.正比例函数y=kx(k≠0)和一次函数y=x﹣k在同一个直角坐标系内的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【考点】一次函数的图象;正比例函数的图象.
【分析】根据正比例函数和一次函数的图象性质并结合其系数作答.
【解答】解:当k>0时,正比例函数图象经过1,3象限,一次函数图象经过1,3,2象限,
当k<0时,正比例函数图象经过2,4象限,一次函数图象经过1,3,4象限.
故选A.
【点评】本题主要考查了一次函数的图象性质和正比例函数的图象性质,关键是由k的取值确定函数所在的象限.
二、填空题(本题满分24分,共有8道小题,每小题3分)
9.的平方根是,1﹣的相反数为﹣1.
【考点】实数的性质;平方根;算术平方根.
【分析】根据开方运算,可得一个数的平方根;根据只有符号不同的两个数互为相反数,可得答案.
【解答】解:=5,5的平方根是,
1﹣的相反数是﹣1,
故答案为:,﹣1.
【点评】本题考查了实数的性质,在一个数的前面加上负号就是这个数的相反数,注意先求算术平方根再求平方根.
10.比较大小:3<4.
【考点】实数大小比较.
【专题】推理填空题;实数.
【分析】首先分别求出3、4的平方的值各是多少;然后根据实数大小比较的方法,判断出3、4的平方的大小关系,即可判断出3、4的大小关系.
【解答】解:(1)=45,(4)2=48,
∵45<48,
∴3<4.
故答案为:<.
【点评】(1)此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
(2)解答此题的关键是比较出3、4这两个数的平方的大小关系.
11.如图,围棋棋盘放置在 ( http: / / www.21cnjy.com )某个平面直角坐标系内,白棋②的坐标为(﹣7,﹣4),白棋④的坐标为(﹣6,﹣8),那么黑棋的坐标应该是(﹣3,﹣7).
( http: / / www.21cnjy.com )
【考点】坐标确定位置.
【分析】根据点的坐标向右平移加,向上平移加,可得答案.
【解答】解:由(﹣6,﹣8)的位置向右平移3个单位,向上平移1个单位,得
﹣6+3=﹣3,﹣8+1=﹣7,
故答案为:(﹣3,﹣7).
【点评】本题考查了坐标确定位置,利用点的坐标向右平移加,向上平移加是解题关键.
12.如图,有一块直角三角形纸片ABC,∠C=90°.两直角边AC=6cm,BC=8cm,现将该纸片沿直线AD折叠,使点C落在斜边AB上的点E处,则折痕AD=3cm.
( http: / / www.21cnjy.com )
【考点】翻折变换(折叠问题).
【分析】先根据勾股定理求得AB的长,再根据折叠的性质求得AE,BE的长,从而利用勾股定理可求得CD的长,然后根据勾股定理即可求得AD.
【解答】解:∵AC=6cm,BC=8cm,∠C=90°
∴AB=10cm,
∵AE=6cm(折叠的性质),
∴BE=4cm,
设CD=x,
则在Rt△DEB中,
42+x2=(8﹣x)2,
∴x=3cm.
∴CD=3cm,
在Rt△ACD中,AD==3cm.
故答案为3.
【点评】本题考查了翻折变换的性质,勾股定理的应用,熟记性质并表示出Rt△DEB的三边,然后利用勾股定理列出方程是解题的关键.
13.如果直线y=ax+b与直线y=﹣2x+3平行,且经过点A(﹣1,1),则b=﹣1.
【考点】两条直线相交或平行问题.
【分析】相互平行的两条直线的一次项系数相等,故此a=﹣2,将a=﹣2,x=﹣1,y=1代入y=ax+b可求得b的值.
【解答】解:∵直线y=ax+b与直线y=﹣2x+3平行,
∴a=﹣2.
∴直线y=ax+b的解析式为y=﹣2x+b.
将x=﹣1,y=1代入得:﹣2×(﹣1)+b=1.
解得:b=﹣1.
故答案为:﹣1.
【点评】本题主要考查的是两条直线平行问题,明确相互平行的两条直线的一次项系数相等是解题的关键.
14.如图,有一圆柱,其 ( http: / / www.21cnjy.com )高为12cm,底面半径为3cm,在圆柱下底面A点处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为15cm.(π取3)
( http: / / www.21cnjy.com )
【考点】平面展开-最短路径问题.
【分析】本题应先把圆柱展开即得其平面展 ( http: / / www.21cnjy.com )开图,则A,B所在的长方形的长为圆柱的高12cm,宽为底面圆周长的一半为πr,蚂蚁经过的最短距离为连接A,B的线段长,由勾股定理求得AB的长.
【解答】解:圆柱展开图为长方形,
则A,B所在的长方形的长为圆柱的高12cm,宽为底面圆周长的一半为πrcm,
蚂蚁经过的最短距离为连接A,B的线段长,
由勾股定理得AB====15cm.
故蚂蚁经过的最短距离为15cm.(π取3)
( http: / / www.21cnjy.com )
【点评】解答本题的关键是计算出圆柱展开后所得长方形长和宽的值,然后用勾股定理计算即可.
15.若x>4,则化简﹣=﹣3.
【考点】二次根式的性质与化简.
【专题】计算题;二次根式.
【分析】根据x的范围判断出x﹣4与1﹣x的正负,利用二次根式性质化简,计算即可得到结果.
【解答】解:∵x>4,
∴x﹣4>0,1﹣x<0,
则原式=|x﹣4|﹣|1﹣x|=x﹣4+1﹣x=﹣3.
故答案为:﹣3.
【点评】此题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.
16.如图,以等腰三角形AOB的斜边为 ( http: / / www.21cnjy.com )直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第n个等腰直角三角形的面积Sn=2n﹣2.
( http: / / www.21cnjy.com )
【考点】等腰直角三角形.
【专题】压轴题;规律型.
【分析】本题要先根据已知的条件求出S1、S2的值,然后通过这两个面积的求解过程得出一般化规律,进而可得出Sn的表达式.
【解答】解:根据直角三角形的面积公式,得S1==2﹣1;
根据勾股定理,得:AB=,则S2=1=20;
A1B=2,则S3=21,
依此类推,发现:Sn=2n﹣2.
【点评】本题要先从简单的例子入手得出一般化的结论,然后根据得出的规律去求特定的值.
三、解答题(本题满分64分)
17.(24分)化简
(1)
(2)3﹣5
(3)(2﹣1)2
(4)
(5)
(6)2﹣.
【考点】二次根式的混合运算.
【专题】计算题.
【分析】(1)利用二次根式的性质化简;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)利用完全平方公式计算;
(4)利用平方差公式计算;
(5)先把各二次根式化为最简二次根式,然后合并即可;
(6)先把化简,然后合并后进行二次根式的除法运算,再进行减法运算.
【解答】解:(1)原式==;
(2)原式=6﹣20=﹣14;
(3)原式=12﹣4+1=13﹣4;
(4)原式=(2)2﹣1=20﹣1=19;
(5)原式=4+﹣=;
(6)原式=2﹣=2﹣3=﹣1.
【点评】本题考查了二次根式的计算: ( http: / / www.21cnjy.com )先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.
18.已知点A(﹣2,﹣1),B(3,1),C(1,4).
(1)在直角坐标系中描出点A、B、C,画出△ABC.
(2)求出△ABC的面积.
(3)作出△ABC在坐标系中关于y轴对称的△A1B1C1.
( http: / / www.21cnjy.com )
【考点】作图-轴对称变换.
【分析】(1)利用已知点在坐标系中得出各点位置即可;
(2)利用△ABC所在矩形面积减去周围三角形面积进而得出答案;
(3)利用关于y轴对称点的性质得出各对应点位置即可得出答案.
【解答】解:(1)如图所示:△ABC即为所求;
(2)S△ABC=5×5﹣×2×3﹣×3×5﹣×2×5=9.5;
(3)如图所示:△A1B1C1,即为所求.
( http: / / www.21cnjy.com )
【点评】此题主要考查了轴对称变换以及三角形面积求法,根据题意得出对应点位置是解题关键.
19.如图所示,有一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积.
( http: / / www.21cnjy.com )
【考点】勾股定理的逆定理;勾股定理.
【分析】连接AC,先利用勾股定理求出AC ( http: / / www.21cnjy.com ),再根据勾股定理的逆定理判定△ABC是直角三角形,那么△ABC的面积减去△ACD的面积就是所求的面积.
【解答】解:如图,连接AC.
在△ACD中,∵AD=4米,CD=3米,∠ADC=90°,
∴AC=5米,
又∵AC2+BC2=52+122=132=AB2,
∴△ABC是直角三角形,
∴这块地的面积=△ABC的面积﹣△ACD的面积=×5×12﹣×3×4=24(平方米).
( http: / / www.21cnjy.com )
【点评】本题考查了勾股定理、勾股定理的逆定理的应用,得到△ABC是直角三角形是解题的关键.同时考查了直角三角形的面积公式.
20.某日通过高速公路收费站的汽车中 ( http: / / www.21cnjy.com ),共有3000辆次缴了通行费,其中大车每辆次缴费20元,小车每辆次缴费10元.设这一天小车缴通行费的辆次为x,总的通行费收入为y元.
(1)试写出y关于x的函数关系式;
(2)若小车缴通行的辆次为1200,这天的通行费收入是多少元?
【考点】一次函数的应用.
【分析】(1)小车有x辆,则大车有(3000﹣x)辆,根据:总通行费=小车通行费+大车通行费,列出函数关系式;
(2)把x=1200代入(1)中的函数关系式即可.
【解答】解:(1)依题意,得y=10x+20(3000﹣x)=﹣10x+60000;
(2)当x=1200时,y=﹣10×1200+60000=48000元.
答:这天的通行费收入是48000元.
【点评】本题考查了一次函数的应用.关键是根据总通行费=小车通行费+大车通行费,列出函数关系式.
21.如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距10千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是1小时.
(3)B出发后3小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?
( http: / / www.21cnjy.com )
【考点】一次函数的应用.
【专题】行程问题.
【分析】(1)根据函数图象可以直接看出B出发时与A相距的路程;
(2)根据函数图象可以得到走了一段路后,自行车发生故障进行修理所用的时间;
(3)根据函数图象可以直接得到B出发后多长时间与A相遇;
(4)根据直线lA经过点(0,10),(3,25)可以求得它的解析式;
(5)根据函数图象可以求得lB的解析式与直线lA联立方程组即可求得相遇的时间.
【解答】解:(1)根据函数图象可知,B出发时与A相距10千米,
故答案为:10;
(2)根据函数图象可知,走了一段路后,自行车发生故障进行修理,所用的时间是1.5﹣0.5=1小时,
故答案为:1;
(3)根据图象可知B出发后3小时时与A相遇;
(4)根据函数图象可知直线lA经过点(0,10),(3,25).
设直线lA的解析式为:S=kt+b,则
解得,k=5,b=10
即A行走的路程S与时间t的函数关系式是:S=5t+10;
(5)设直线lB的解析式为:S=kt,
∵点(0.5,7.5)在直线lB上,
∴7.5=k×0.5
得k=15
∴S=15t.
∴
解得S=15,t=1.
故若B的自行车不发生故障,保持出发时的速度前进,1小时时与A相遇.
【点评】本题考查一次函数的应用,解体的关键是利用数形结合的思想对图象进行分析,找出所求问题需要的条件.
22.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+=(1+)2.善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为整数),则有a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=,用含m、n的式子分别表示a、b,得:a=m2+3n2,b=2mn;
(2)利用所探索的结论,找一组正整数a、b、m、n填空:4+2=(1+1)2;
(3)若a+4=,且a、m、n均为正整数,求a的值?
【考点】二次根式的混合运算.
【分析】(1)根据完全平方公式运算法则,即可得出a、b的表达式;
(2)首先确定好m、n的正整数值,然后根据(1)的结论即可求出a、b的值;
(3)根据题意,4=2mn,首先确定m、n的值,通过分析m=2,n=1或者m=1,n=2,然后即可确定好a的值.
【解答】解:(1)∵a+b=,
∴a+b=m2+3n2+2mn,
∴a=m2+3n2,b=2mn.
故答案为:m2+3n2,2mn.
(2)设m=1,n=1,
∴a=m2+3n2=4,b=2mn=2.
故答案为4、2、1、1.
(3)由题意,得:
a=m2+3n2,b=2mn
∵4=2mn,且m、n为正整数,
∴m=2,n=1或者m=1,n=2,
∴a=22+3×12=7,或a=12+3×22=13.
【点评】本题主要考查二次根式的混合运算,完全平方公式,解题的关键在于熟练运算完全平方公式和二次根式的运算法则.
同课章节目录
