浙教版数学九年级上册期中复习题二(含答案)
文档属性
| 名称 | 浙教版数学九年级上册期中复习题二(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 324.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-12 17:11:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版数学(2024)九年级上册期中复习题二
一、单选题
1.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P的概率是( )
A. B. C. D.1
2.将一个各面涂有颜色的正方体,分割成同样大小的27个小正方体,从这些正方体中任取一个,恰有3个面涂有颜色的概率是
A. B. C. D.
3.下列事件为必然事件的是( )
A.打开电视,正在播放新闻
B.买一张电影票,座位号是奇数号
C.任意画一个三角形,其内角和是180°
D.掷一枚质地均匀的硬币,正面朝上
4.分别写有数字-1,-2,1,3,4的五张卡片,除数字外其他均相同,将它们背面朝上,从中任抽一张,抽到负数的概率是( )
A. B. C. D.
5.下列事件中,是确定性事件的是( )
A.篮球队员在罚球线上投篮一次,未投中
B.经过有交通信号灯的路口,遇到绿灯
C.任意画一个三角形,其外角和是360°
D.投掷一枚骰子,向上一面的点数大于3
6.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A. B. C. D.
7.已知二次函数y=2x2﹣2(a+b)x+a2+b2,a,b为常数,当y达到最小值时,x的值为( )
A.a+b B. C.﹣2ab D.
8.如图,小彬收集了三张除正面图案外完全相同的卡片,其中两张印有中国国际进口博览会的标志,另外一张印有进博会吉祥物“进宝”.现将三张卡片背面朝上放置,搅匀后从中一次性随机抽取两张,则抽到的两张卡片图案不相同的概率为( )
A. B. C. D.
9.二次函数的图象如图所示,对称轴为.给出下列结论:①;②;③;④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.已知二次函数 (a<0)的图象过点(1,0)和(x1,0),且﹣2<x1<﹣1,下列4个判断中:①a+b=-1;②a>b﹣1;③b﹣a<0;④﹣1<a<﹣ ,正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
11.从,,0,1,2这五个数中任取一个数作为a的值,则抛物线开口向下的概率是 .
12.如图,要修建一个圆形喷水池,在池中心竖直安装一根长度为水管,在水管的顶端点处安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离处达到最高,水柱落地处离池中心距离,则抛物线形水柱的最高点到地面的距离是 .
13.有五张正面写有数字,、0,1,4的卡片,卡片除数字外其余完全相同,将其背面向上并洗匀,随机抽取1张记下数字,不放回再随机抽取1张,那么抽取的两张卡片上的数字之积为非负数的概率是
14.抛物线y=(1-k)x2-2x-1与x轴有两个交点,则k的取值范围是 .
15.如图,一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m;那么当水位下降1m后,水面的宽度为 m.
16.如图1,E是等边ΔABC的边BC上一点(不与点B,C重合),连接AE,以AE为边向右作等边ΔAEF,连接CF.已知ΔECF的面积S与BE的长x之间的函数关系图象是如图2所示的抛物线,且点P为抛物线的顶点.
(1)请根据抛物线的对称性,判断当ΔECF的面积最大时,∠FEC= °.
(2)等边ΔABC的边长为 .
三、解答题
17.第一盒中有2个白球、1个红球,第二盒中有1个白球、1个红球,这些球除颜色外无其他差别,分别从每个盒中随机取出1个球.
在第一盒中取出1个球是白球的概率是______;
求取出的2个球中1个白球、1个红球的概率.
18.如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这六个数字.同时转动两个转盘各一次(指针落在等分线时重转),转盘自由停止后,A转盘中指针指向的数字记为,B转盘中指针指向的数字记为,点的坐标记为.
(1)用列表法或画树状图表示所有可能出现的结果.
(2)求出落在第四象限的概率.
19.2019年11月1日5G商用套餐正式上线. 某移动营业厅为了吸引用户,设计了A,B两个可以自由转动的转盘(如图),A转盘被等分为2个扇形,分别为红色和黄色;B转盘被等分为3个扇形,分别为黄色、红色、蓝色,指针固定不动. 营业厅规定,每位5G新用户可分别转动两个转盘各一次,转盘停止后,若指针所指区域颜色相同,则该用户可免费领取100G通用流量(若指针停在分割线上,则视其指向分割线右侧的扇形). 小王办理5G业务获得一次转转盘的机会,求他能免费领取100G通用流量的概率.
20.已知抛物线的C1顶点为E(﹣1,4),与y轴交于C(0,3).
(1)求抛物线C1的解析式;
(2)如图1,过顶点E作EF⊥x轴于F点,交直线AC于D,点P、Q分别在抛物线C1和x轴上,若Q为(t,0),且以E、D、P、Q为顶点的四边形为平行四边形,求t的值;
(3)如图2,将抛物线C1向右平移一个单位得到抛物线C2,直线y=kx+6与y轴交于点H,与抛物线C2交于M、N两个不同点,分别过M、N两点作y轴的垂线,垂足分别为P、Q,当k的值在取值范围内发生变化时,式子+的值是否发生变化?若不变,请求其值.(解此题时不用相似知识)
四、计算题
21.商店促销,设了有两种摇奖方式:
方式一:如图1,有一枚均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这个骰子掷出后,“6”朝上的则获奖:
图1 图2
方式二:如图2,一个均匀的转盘被等分成12份,分别标有1,2,3,4,5,6,7,8,9,10,11,12这12个数字.转动转盘,当转盘停止后,指针指向的数字为3的倍数则获奖.
小明想增加获奖机会,应选择哪种摇奖方式?请通过计算,应用概率相关知识说明理由.
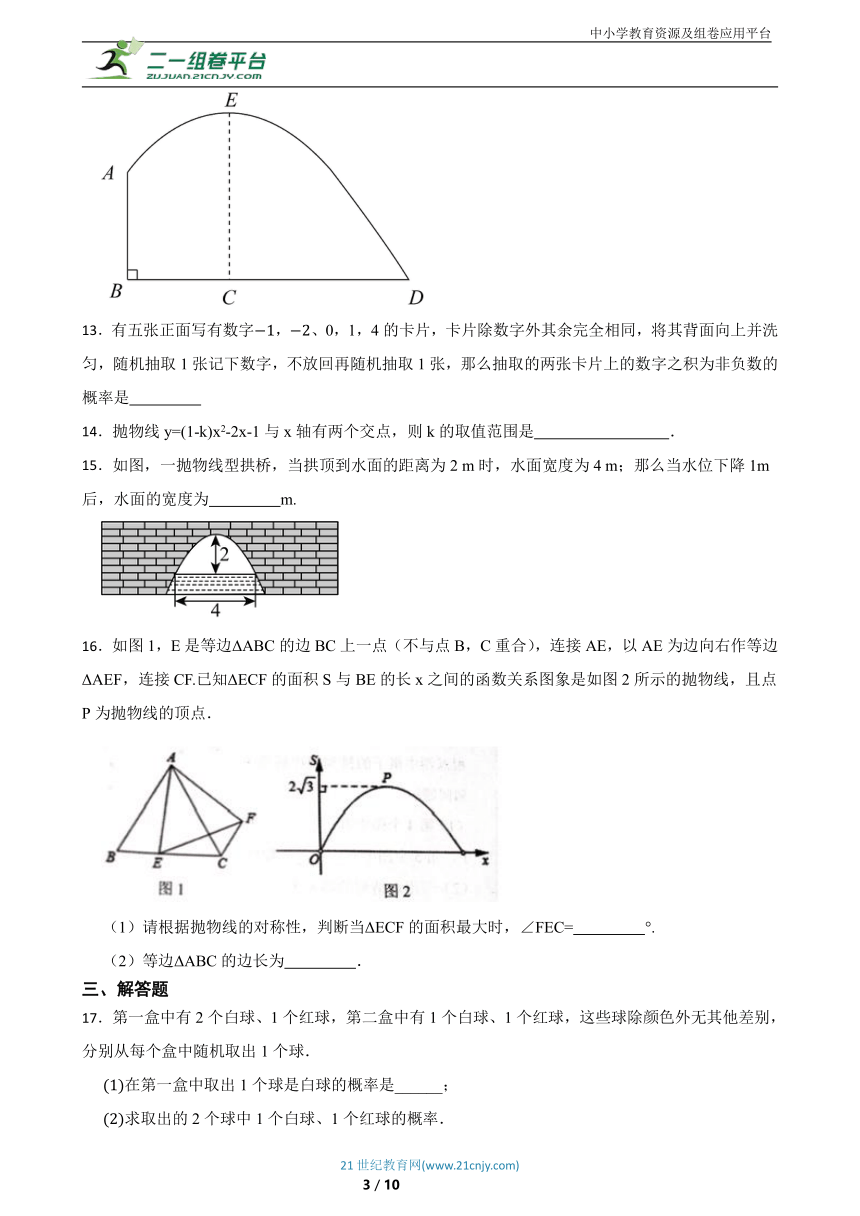
22.如图,在平面直角坐标系中,是等腰直角三角形,,,,抛物线过点C.
(1)求点C的坐标.
(2)求抛物线的表达式.
23.如图,已知抛物线经过原点和轴上另一点,它的对称轴与轴交于点,直线经过抛物线上一点,且与轴、直线分别交于点、,点是的中点.
(1)求的值;
(2)求该抛物线对应的函数关系式;
(3)若是该抛物线上的一个动点,是否存在这样的点,使得?若存在,试求出所有符合条件的点的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】概率公式
2.【答案】D
【知识点】概率公式
3.【答案】C
【知识点】事件发生的可能性
4.【答案】C
【知识点】概率公式
5.【答案】C
【知识点】事件发生的可能性
6.【答案】A
【知识点】用列表法或树状图法求概率;概率公式
7.【答案】B
【知识点】二次函数的最值
8.【答案】D
【知识点】用列表法或树状图法求概率
9.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征
10.【答案】B
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的性质
11.【答案】
【知识点】概率公式
12.【答案】5
【知识点】二次函数的实际应用-喷水问题
13.【答案】
【知识点】用列表法或树状图法求概率
14.【答案】k<2,且k≠1
【知识点】二次函数图象与坐标轴的交点问题
15.【答案】2
【知识点】二次函数的实际应用-拱桥问题
16.【答案】(1)30
(2)
【知识点】二次函数的最值;三角形的面积;等边三角形的性质;二次函数y=ax²+bx+c的性质
17.【答案】(1);(2).
【知识点】用列表法或树状图法求概率
18.【答案】(1),,,,,,,,
(2)
【知识点】用列表法或树状图法求概率
19.【答案】解:先将转盘A记作红1,黄1,转盘B记作红2,黄2,蓝
转盘A 转盘B 红2 黄2 蓝
红1 (红1,红2) (红1,黄2) (红1,蓝)
黄1 (黄1,红2) (黄1,黄2) (黄1,蓝)
总共有6种结果,每种结果出现的可能性相同,
其中两次转盘指向区域颜色相同的结果有2种:(红1,红2),(黄1,黄2),
所以,P(能免费领取100G通用流量)= .
【知识点】用列表法或树状图法求概率;概率公式
20.【答案】解:(1)设抛物线C1的解析式为:y=a(x+1)2+4,把点C(0,3)的坐标代入得,a=1,
故抛物线C1的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3;
(2)如图1,
由题意得,PQ∥DE,
由点P(t,0),得点Q(t,﹣t2﹣2t+3),
所以有:PQ=|﹣t2﹣2t+3|,
y=﹣(x+1)2+4,令y=0,解得:x=﹣3,或x=1,
∴点A(﹣3,0),
运用两点法可求直线AC的解析式为:y=x+3,
当x=﹣1时,y=2,
∴点D(﹣1,2),
DE=4﹣2=2,
由平行四边形性质可得:PQ=DE,
|﹣t2﹣2t+3|=2,
解得:t=-1,或t=﹣1;
(3)如图2,
抛物线C1向右平移一个单位得到抛物线C2的解析式为:y=﹣x2+4,
联立方程组:,
解得:x=,y=,
∴HP=,HQ=,
HP+HQ=k2,HP×HQ=2k2,
∴+==
【知识点】二次函数图象的几何变换;二次函数的实际应用-几何问题
21.【答案】方式二获奖机会大,选方式二
【知识点】游戏公平性
22.【答案】(1)点C的坐标
(2)
【知识点】待定系数法求二次函数解析式
23.【答案】(1)
(2)
(3)或
【知识点】待定系数法求二次函数解析式
21世纪教育网(www.21cnjy.com)
1 / 1
浙教版数学(2024)九年级上册期中复习题二
一、单选题
1.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P的概率是( )
A. B. C. D.1
2.将一个各面涂有颜色的正方体,分割成同样大小的27个小正方体,从这些正方体中任取一个,恰有3个面涂有颜色的概率是
A. B. C. D.
3.下列事件为必然事件的是( )
A.打开电视,正在播放新闻
B.买一张电影票,座位号是奇数号
C.任意画一个三角形,其内角和是180°
D.掷一枚质地均匀的硬币,正面朝上
4.分别写有数字-1,-2,1,3,4的五张卡片,除数字外其他均相同,将它们背面朝上,从中任抽一张,抽到负数的概率是( )
A. B. C. D.
5.下列事件中,是确定性事件的是( )
A.篮球队员在罚球线上投篮一次,未投中
B.经过有交通信号灯的路口,遇到绿灯
C.任意画一个三角形,其外角和是360°
D.投掷一枚骰子,向上一面的点数大于3
6.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A. B. C. D.
7.已知二次函数y=2x2﹣2(a+b)x+a2+b2,a,b为常数,当y达到最小值时,x的值为( )
A.a+b B. C.﹣2ab D.
8.如图,小彬收集了三张除正面图案外完全相同的卡片,其中两张印有中国国际进口博览会的标志,另外一张印有进博会吉祥物“进宝”.现将三张卡片背面朝上放置,搅匀后从中一次性随机抽取两张,则抽到的两张卡片图案不相同的概率为( )
A. B. C. D.
9.二次函数的图象如图所示,对称轴为.给出下列结论:①;②;③;④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.已知二次函数 (a<0)的图象过点(1,0)和(x1,0),且﹣2<x1<﹣1,下列4个判断中:①a+b=-1;②a>b﹣1;③b﹣a<0;④﹣1<a<﹣ ,正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
11.从,,0,1,2这五个数中任取一个数作为a的值,则抛物线开口向下的概率是 .
12.如图,要修建一个圆形喷水池,在池中心竖直安装一根长度为水管,在水管的顶端点处安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离处达到最高,水柱落地处离池中心距离,则抛物线形水柱的最高点到地面的距离是 .
13.有五张正面写有数字,、0,1,4的卡片,卡片除数字外其余完全相同,将其背面向上并洗匀,随机抽取1张记下数字,不放回再随机抽取1张,那么抽取的两张卡片上的数字之积为非负数的概率是
14.抛物线y=(1-k)x2-2x-1与x轴有两个交点,则k的取值范围是 .
15.如图,一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m;那么当水位下降1m后,水面的宽度为 m.
16.如图1,E是等边ΔABC的边BC上一点(不与点B,C重合),连接AE,以AE为边向右作等边ΔAEF,连接CF.已知ΔECF的面积S与BE的长x之间的函数关系图象是如图2所示的抛物线,且点P为抛物线的顶点.
(1)请根据抛物线的对称性,判断当ΔECF的面积最大时,∠FEC= °.
(2)等边ΔABC的边长为 .
三、解答题
17.第一盒中有2个白球、1个红球,第二盒中有1个白球、1个红球,这些球除颜色外无其他差别,分别从每个盒中随机取出1个球.
在第一盒中取出1个球是白球的概率是______;
求取出的2个球中1个白球、1个红球的概率.
18.如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这六个数字.同时转动两个转盘各一次(指针落在等分线时重转),转盘自由停止后,A转盘中指针指向的数字记为,B转盘中指针指向的数字记为,点的坐标记为.
(1)用列表法或画树状图表示所有可能出现的结果.
(2)求出落在第四象限的概率.
19.2019年11月1日5G商用套餐正式上线. 某移动营业厅为了吸引用户,设计了A,B两个可以自由转动的转盘(如图),A转盘被等分为2个扇形,分别为红色和黄色;B转盘被等分为3个扇形,分别为黄色、红色、蓝色,指针固定不动. 营业厅规定,每位5G新用户可分别转动两个转盘各一次,转盘停止后,若指针所指区域颜色相同,则该用户可免费领取100G通用流量(若指针停在分割线上,则视其指向分割线右侧的扇形). 小王办理5G业务获得一次转转盘的机会,求他能免费领取100G通用流量的概率.
20.已知抛物线的C1顶点为E(﹣1,4),与y轴交于C(0,3).
(1)求抛物线C1的解析式;
(2)如图1,过顶点E作EF⊥x轴于F点,交直线AC于D,点P、Q分别在抛物线C1和x轴上,若Q为(t,0),且以E、D、P、Q为顶点的四边形为平行四边形,求t的值;
(3)如图2,将抛物线C1向右平移一个单位得到抛物线C2,直线y=kx+6与y轴交于点H,与抛物线C2交于M、N两个不同点,分别过M、N两点作y轴的垂线,垂足分别为P、Q,当k的值在取值范围内发生变化时,式子+的值是否发生变化?若不变,请求其值.(解此题时不用相似知识)
四、计算题
21.商店促销,设了有两种摇奖方式:
方式一:如图1,有一枚均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这个骰子掷出后,“6”朝上的则获奖:
图1 图2
方式二:如图2,一个均匀的转盘被等分成12份,分别标有1,2,3,4,5,6,7,8,9,10,11,12这12个数字.转动转盘,当转盘停止后,指针指向的数字为3的倍数则获奖.
小明想增加获奖机会,应选择哪种摇奖方式?请通过计算,应用概率相关知识说明理由.
22.如图,在平面直角坐标系中,是等腰直角三角形,,,,抛物线过点C.
(1)求点C的坐标.
(2)求抛物线的表达式.
23.如图,已知抛物线经过原点和轴上另一点,它的对称轴与轴交于点,直线经过抛物线上一点,且与轴、直线分别交于点、,点是的中点.
(1)求的值;
(2)求该抛物线对应的函数关系式;
(3)若是该抛物线上的一个动点,是否存在这样的点,使得?若存在,试求出所有符合条件的点的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】概率公式
2.【答案】D
【知识点】概率公式
3.【答案】C
【知识点】事件发生的可能性
4.【答案】C
【知识点】概率公式
5.【答案】C
【知识点】事件发生的可能性
6.【答案】A
【知识点】用列表法或树状图法求概率;概率公式
7.【答案】B
【知识点】二次函数的最值
8.【答案】D
【知识点】用列表法或树状图法求概率
9.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征
10.【答案】B
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的性质
11.【答案】
【知识点】概率公式
12.【答案】5
【知识点】二次函数的实际应用-喷水问题
13.【答案】
【知识点】用列表法或树状图法求概率
14.【答案】k<2,且k≠1
【知识点】二次函数图象与坐标轴的交点问题
15.【答案】2
【知识点】二次函数的实际应用-拱桥问题
16.【答案】(1)30
(2)
【知识点】二次函数的最值;三角形的面积;等边三角形的性质;二次函数y=ax²+bx+c的性质
17.【答案】(1);(2).
【知识点】用列表法或树状图法求概率
18.【答案】(1),,,,,,,,
(2)
【知识点】用列表法或树状图法求概率
19.【答案】解:先将转盘A记作红1,黄1,转盘B记作红2,黄2,蓝
转盘A 转盘B 红2 黄2 蓝
红1 (红1,红2) (红1,黄2) (红1,蓝)
黄1 (黄1,红2) (黄1,黄2) (黄1,蓝)
总共有6种结果,每种结果出现的可能性相同,
其中两次转盘指向区域颜色相同的结果有2种:(红1,红2),(黄1,黄2),
所以,P(能免费领取100G通用流量)= .
【知识点】用列表法或树状图法求概率;概率公式
20.【答案】解:(1)设抛物线C1的解析式为:y=a(x+1)2+4,把点C(0,3)的坐标代入得,a=1,
故抛物线C1的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3;
(2)如图1,
由题意得,PQ∥DE,
由点P(t,0),得点Q(t,﹣t2﹣2t+3),
所以有:PQ=|﹣t2﹣2t+3|,
y=﹣(x+1)2+4,令y=0,解得:x=﹣3,或x=1,
∴点A(﹣3,0),
运用两点法可求直线AC的解析式为:y=x+3,
当x=﹣1时,y=2,
∴点D(﹣1,2),
DE=4﹣2=2,
由平行四边形性质可得:PQ=DE,
|﹣t2﹣2t+3|=2,
解得:t=-1,或t=﹣1;
(3)如图2,
抛物线C1向右平移一个单位得到抛物线C2的解析式为:y=﹣x2+4,
联立方程组:,
解得:x=,y=,
∴HP=,HQ=,
HP+HQ=k2,HP×HQ=2k2,
∴+==
【知识点】二次函数图象的几何变换;二次函数的实际应用-几何问题
21.【答案】方式二获奖机会大,选方式二
【知识点】游戏公平性
22.【答案】(1)点C的坐标
(2)
【知识点】待定系数法求二次函数解析式
23.【答案】(1)
(2)
(3)或
【知识点】待定系数法求二次函数解析式
21世纪教育网(www.21cnjy.com)
1 / 1
同课章节目录
