北师大版数学八年级上册期中复习题一(含答案)
文档属性
| 名称 | 北师大版数学八年级上册期中复习题一(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 242.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-12 17:37:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版数学(2024)八年级上册期中复习题一
一、单选题
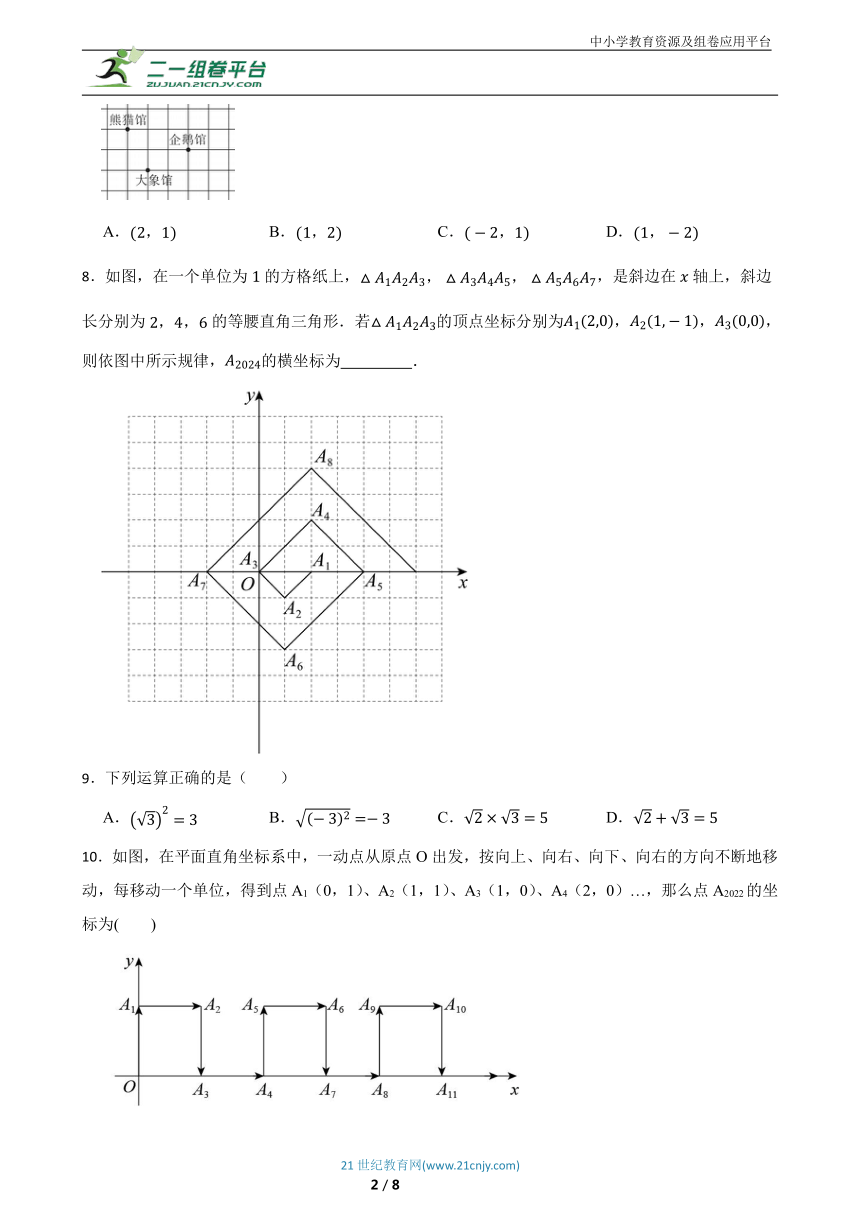
1.如图,圆柱形开口杯底部固定在长方体水池底,向水池匀速注入水(倒在杯外),水池中水面高度为,注水时间为,则与之间的关系大致为下图中的
A. B.
C. D.
2.一个三角形的边长分别为,则此三角形的周长为( )
A.10和11之间 B.5和6之间 C.6和7之间 D.9和10之间
3.对于实数、,定义运算“※”如下:,则的平方根为( )
A.4 B.2 C. D.
4.在平面直角坐标中,点A(4,-1)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.以下列各组数为边长,能构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.,, D.,,
6. 计算:=( )
A. B. C. D.1
7.小林在学习平面直角坐标系后,将如图所示的动物园的部分地图与平面直角坐标系联系起来,若“大象馆”的坐标为,“熊猫馆”的坐标为,则“企鹅馆”的坐标为( )
A. B. C. D.
8.如图,在一个单位为的方格纸上,,是斜边在轴上,斜边长分别为的等腰直角三角形.若的顶点坐标分别为,,,则依图中所示规律,的横坐标为 .
9.下列运算正确的是( )
A. B. C. D.
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2022的坐标为( )
A.(1011,0) B.(1011,1) C.(2022,0) D.(2022,1)
二、填空题
11.点M(-1,3)关于x轴对称的点N的坐标是
12.与最接近的整数是 .
13.计算: .
14.一根高9m的旗杆在离地4m高处折断,折断处仍相连,此时在3.9m远处耍的身高为1m的小明 危险.(填有或无)
15.小亮在一张长为,宽为的矩形纸片上,剪了一个腰长为的等腰三角形(要求等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上),则这个等腰三角形的底边为 .
16.如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2019的坐标为 .
三、计算题
17.计算:
18.
(1)计算: ;
(2)已知 ,求代数式 的值.
19.阅读下列解题过程:,
,
请回答下列问题:
(1)观察上面的解答过程,请写出 ;
(2)利用上面的解法,请化简:
(3)比较大小:和.
四、解答题
20.已知,求的值.
21.分别求下列各数的绝对值和相反数:
(1).
(2).
(3)-π.
22. 在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
23.联想三角形外心的概念,我们可引入如下概念.
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= AB,求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
答案解析部分
1.【答案】B
【知识点】函数的图象
2.【答案】A
【知识点】无理数的估值;二次根式的加减法
3.【答案】C
【知识点】有理数混合运算法则(含乘方);开平方(求平方根)
4.【答案】D
【知识点】点的坐标与象限的关系
5.【答案】C
【知识点】勾股定理的逆定理
6.【答案】B
【知识点】二次根式的性质与化简
7.【答案】B
【知识点】点的坐标
8.【答案】
【知识点】点的坐标
9.【答案】A
【知识点】二次根式的乘除法;二次根式的加减法;二次根式的化简求值
10.【答案】B
【知识点】点的坐标
11.【答案】(-1,-3)
【知识点】关于坐标轴对称的点的坐标特征
12.【答案】6
【知识点】无理数的估值
13.【答案】
【知识点】二次根式的加减法
14.【答案】有
【知识点】勾股定理
15.【答案】或或
【知识点】等腰三角形的性质;勾股定理
16.【答案】(-505,505)
【知识点】点的坐标;探索图形规律
17.【答案】
【知识点】负整数指数幂;二次根式的混合运算;化简含绝对值有理数
18.【答案】(1)解:原式
(2)解:原式
,
将 代入原式得,
【知识点】代数式求值;二次根式的混合运算
19.【答案】(1) ;(2)9;(3)
【知识点】分母有理化;二次根式的混合运算
20.【答案】
【知识点】二次根式的性质与化简;二次根式的乘除法;算术平方根的性质(双重非负性)
21.【答案】(1) 的绝对值是,相反数是;
(2) 的绝对值是,相反数是;
(3)-π 的绝对值是π,相反数是π.
【知识点】实数的相反数;实数的绝对值
22.【答案】解:∵在中,,,,
∴,
∵此人以0.5m/s的速度收绳.10s后船移动到点D的位置,
∴,
∴,
∴.
答:船向岸边移动了米.
【知识点】勾股定理的应用
23.【答案】应用:解:①若PB=PC,连接PB,则∠PCB=∠PBC,
∵CD为等边三角形的高,
∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,
∴PD= DB= AB,
与已知PD= AB矛盾,∴PB≠PC,
②若PA=PC,连接PA,同理可得PA≠PC,
③若PA=PB,由PD= AB,得PD=BD,
∴∠APD=45°,
故∠APB=90°;
探究:解:∵BC=5,AB=3,
∴AC= = =4,
① 若PB=PC,设PA=x,则x2+32=(4﹣x)2,
∴x= ,即PA= ,
②若PA=PC,则PA=2,
③若PA=PB,由图知,在Rt△PAB中,不可能.
故PA=2或 .
【知识点】线段垂直平分线的性质;等腰三角形的性质;等边三角形的性质;勾股定理
21世纪教育网(www.21cnjy.com)
1 / 1
北师大版数学(2024)八年级上册期中复习题一
一、单选题
1.如图,圆柱形开口杯底部固定在长方体水池底,向水池匀速注入水(倒在杯外),水池中水面高度为,注水时间为,则与之间的关系大致为下图中的
A. B.
C. D.
2.一个三角形的边长分别为,则此三角形的周长为( )
A.10和11之间 B.5和6之间 C.6和7之间 D.9和10之间
3.对于实数、,定义运算“※”如下:,则的平方根为( )
A.4 B.2 C. D.
4.在平面直角坐标中,点A(4,-1)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.以下列各组数为边长,能构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.,, D.,,
6. 计算:=( )
A. B. C. D.1
7.小林在学习平面直角坐标系后,将如图所示的动物园的部分地图与平面直角坐标系联系起来,若“大象馆”的坐标为,“熊猫馆”的坐标为,则“企鹅馆”的坐标为( )
A. B. C. D.
8.如图,在一个单位为的方格纸上,,是斜边在轴上,斜边长分别为的等腰直角三角形.若的顶点坐标分别为,,,则依图中所示规律,的横坐标为 .
9.下列运算正确的是( )
A. B. C. D.
10.如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2022的坐标为( )
A.(1011,0) B.(1011,1) C.(2022,0) D.(2022,1)
二、填空题
11.点M(-1,3)关于x轴对称的点N的坐标是
12.与最接近的整数是 .
13.计算: .
14.一根高9m的旗杆在离地4m高处折断,折断处仍相连,此时在3.9m远处耍的身高为1m的小明 危险.(填有或无)
15.小亮在一张长为,宽为的矩形纸片上,剪了一个腰长为的等腰三角形(要求等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上),则这个等腰三角形的底边为 .
16.如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2019的坐标为 .
三、计算题
17.计算:
18.
(1)计算: ;
(2)已知 ,求代数式 的值.
19.阅读下列解题过程:,
,
请回答下列问题:
(1)观察上面的解答过程,请写出 ;
(2)利用上面的解法,请化简:
(3)比较大小:和.
四、解答题
20.已知,求的值.
21.分别求下列各数的绝对值和相反数:
(1).
(2).
(3)-π.
22. 在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
23.联想三角形外心的概念,我们可引入如下概念.
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= AB,求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
答案解析部分
1.【答案】B
【知识点】函数的图象
2.【答案】A
【知识点】无理数的估值;二次根式的加减法
3.【答案】C
【知识点】有理数混合运算法则(含乘方);开平方(求平方根)
4.【答案】D
【知识点】点的坐标与象限的关系
5.【答案】C
【知识点】勾股定理的逆定理
6.【答案】B
【知识点】二次根式的性质与化简
7.【答案】B
【知识点】点的坐标
8.【答案】
【知识点】点的坐标
9.【答案】A
【知识点】二次根式的乘除法;二次根式的加减法;二次根式的化简求值
10.【答案】B
【知识点】点的坐标
11.【答案】(-1,-3)
【知识点】关于坐标轴对称的点的坐标特征
12.【答案】6
【知识点】无理数的估值
13.【答案】
【知识点】二次根式的加减法
14.【答案】有
【知识点】勾股定理
15.【答案】或或
【知识点】等腰三角形的性质;勾股定理
16.【答案】(-505,505)
【知识点】点的坐标;探索图形规律
17.【答案】
【知识点】负整数指数幂;二次根式的混合运算;化简含绝对值有理数
18.【答案】(1)解:原式
(2)解:原式
,
将 代入原式得,
【知识点】代数式求值;二次根式的混合运算
19.【答案】(1) ;(2)9;(3)
【知识点】分母有理化;二次根式的混合运算
20.【答案】
【知识点】二次根式的性质与化简;二次根式的乘除法;算术平方根的性质(双重非负性)
21.【答案】(1) 的绝对值是,相反数是;
(2) 的绝对值是,相反数是;
(3)-π 的绝对值是π,相反数是π.
【知识点】实数的相反数;实数的绝对值
22.【答案】解:∵在中,,,,
∴,
∵此人以0.5m/s的速度收绳.10s后船移动到点D的位置,
∴,
∴,
∴.
答:船向岸边移动了米.
【知识点】勾股定理的应用
23.【答案】应用:解:①若PB=PC,连接PB,则∠PCB=∠PBC,
∵CD为等边三角形的高,
∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,
∴PD= DB= AB,
与已知PD= AB矛盾,∴PB≠PC,
②若PA=PC,连接PA,同理可得PA≠PC,
③若PA=PB,由PD= AB,得PD=BD,
∴∠APD=45°,
故∠APB=90°;
探究:解:∵BC=5,AB=3,
∴AC= = =4,
① 若PB=PC,设PA=x,则x2+32=(4﹣x)2,
∴x= ,即PA= ,
②若PA=PC,则PA=2,
③若PA=PB,由图知,在Rt△PAB中,不可能.
故PA=2或 .
【知识点】线段垂直平分线的性质;等腰三角形的性质;等边三角形的性质;勾股定理
21世纪教育网(www.21cnjy.com)
1 / 1
同课章节目录
