广东省深圳市盐田区实验学校2024—2025学年上学期八年级10月月考数学试卷(图片版,无答案)
文档属性
| 名称 | 广东省深圳市盐田区实验学校2024—2025学年上学期八年级10月月考数学试卷(图片版,无答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 21:27:40 | ||
图片预览

文档简介
盐田实验学校 2024-2025 学年度
第一学期 10 月集中练习
初二数学
考试范围:第一至第三章 ;考试时间:100 分钟
一.选择题(共 8 小题,共 24 分)
1.下列实数 ,0.3, , , , ,0.1010010001…(相邻两个 1 之间依
次增加一个 0),其中无理数有( )
A.1 个 B.2 个 C.3 个 D.4 个
2.下列运算正确的是( )
A. B. C. D.
3.如图,小明用手盖住的点的坐标可能为( )
第 6 题
A.(3,2) B.(﹣3,2) C.(3,﹣2) D.(﹣3,﹣2)
4. △ABC 中,∠A,∠B,∠C 的对边分别记为 a,b,c,由下列条件不能判定△ABC 为直
角三角形的是( )
A. ∠A+∠B=∠C B. ∠A:∠B:∠C=1:2:3
C. a2 c2 b2 D. a:b:c=4:4:6
5.估计 +1 的值应在( )
A.3 和 4 之间 B.4 和 5 之间 C.5 和 6 之间 D.6 和 7 之间
6.如图所示,正方形 ABGF 和正方形 CDBE 的面积分别是 100 和 36,则以 AD 为直径的半
圆的面积是( )
A.4π B.8π C.12π D.16π
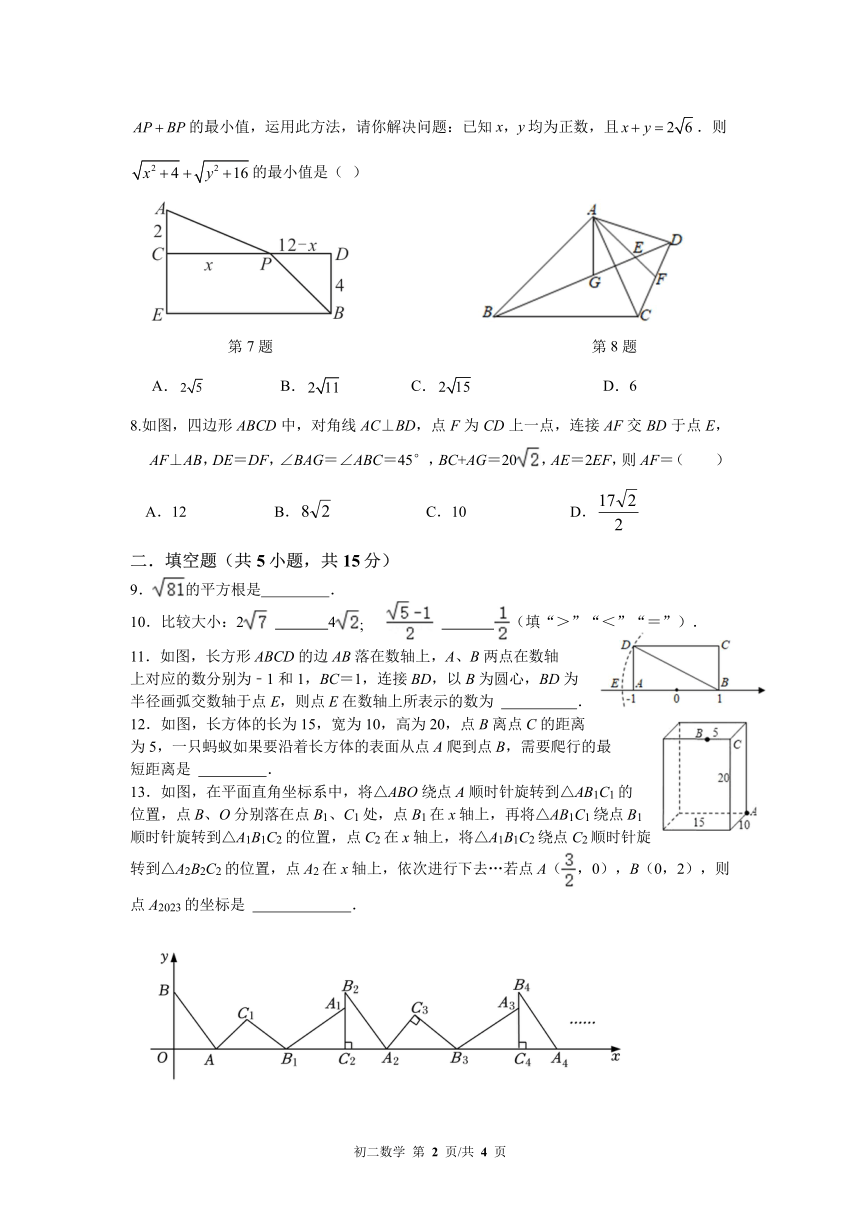
7.数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有
价值的东西,这是数学解题的一个重要原则”.在复习二次根式时,老师提出了一个求代数
式最小值的问题,如: “当0 x 12时,求代数式 2 的最小值”,x 4 12 x 2 16
其中 x2 4 可看作两直角边分别为 x 和 2 的Rt ACP的斜边长, 可看作12 x 2 16
两直角边分别是12 x和 3 的Rt BDP的斜边长.于是构造出如图,将问题转化为求
初二数学 第 1 页/共 4 页
{#{QQABCQaeEs4oggCQggAspTAAACAAA4gKCUU0wVVYICgsEQQskIOBAgLAeAgSEggGQgCBNAuMAsYACIACCJQFIFAKBAC=A}#=}}#}
AP BP 的最小值,运用此方法,请你解决问题:已知 x,y 均为正数,且 x y 2 6 .则
x2 4 y2 16 的最小值是( )
第 7 题 第 8 题
A. 2 5 B.2 11 C.2 15 D.6
8.如图,四边形 ABCD 中,对角线 AC⊥BD,点 F 为 CD 上一点,连接 AF 交 BD 于点 E,
AF⊥AB,DE=DF,∠BAG=∠ABC=45°,BC+AG=20 ,AE=2EF,则 AF=( )
17 2
A.12 B.8 2 C.10 D.
2
二.填空题(共 5 小题,共 15 分)
9. 的平方根是 .
10.比较大小:2 4 ; (填“>”“<”“=”).
11.如图,长方形 ABCD 的边 AB 落在数轴上,A、B 两点在数轴
上对应的数分别为﹣1 和 1,BC=1,连接 BD,以 B 为圆心,BD 为
半径画弧交数轴于点 E,则点 E 在数轴上所表示的数为 .
12.如图,长方体的长为 15,宽为 10,高为 20,点 B 离点 C 的距离
为 5,一只蚂蚁如果要沿着长方体的表面从点 A 爬到点 B,需要爬行的最
短距离是 .
13.如图,在平面直角坐标系中,将△ABO 绕点 A 顺时针旋转到△AB1C1 的
位置,点 B、O 分别落在点 B1、C1 处,点 B1 在 x 轴上,再将△AB1C1 绕点 B1
顺时针旋转到△A1B1C2 的位置,点 C2 在 x 轴上,将△A1B1C2 绕点 C2 顺时针旋
转到△A2B2C2 的位置,点 A2 在 x 轴上,依次进行下去…若点 A( ,0),B(0,2),则
点 A2023 的坐标是 .
初二数学 第 2 页/共 4 页
{#{QQABCQeaEs4oggCQggAspTAAACAAA4gKCUU0wVVYICgsEQQskIOBAgLAeAgSEggGQgCBNAuMAsYACIACCJQFIFAKBAC=A}#=}}#}
三.解答题(共 7 小题,其中第 14 题 15 分,第 15 题 8 分,第 16 题 5 分,第
17 题 8 分,第 18 题 8 分,第 19 题 7 分,第 20 题 10 分,共计 61 分)
14.(1)(6 分)解方程:
①2x2=32; ②8(x﹣1)3=27.
(2)(9 分)计算:
2
① ; ② ( 3 2)( 3 2) 6 ;
3
③ 2023 0 3 1 3 8 12 ;
15.(8 分)已知点 P(a﹣2,2a+8),分别根据下列条件求出点 P 的坐标.
(1)点 P 在 x 轴上;
(2)点 Q 的坐标为(1,5),直线 PQ∥y 轴;
(4)点 P 到 x 轴、y 轴的距离相等.
16.(5 分)在海洋上有一近似于四边形的岛屿,其平面如图①,
小明据此画出该岛的一个数学模型(如图②四边形 ABCD),AC
是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5 千米,
CD= 千米,AD=4 千米.求四边形 ABCD 的面积.
(结果保留根号)
`17.(8 分)如图,已知网格上每个小的正方形的边长为 1
(长度单位),点 A、B、C 在格点上.
(1) 直接在平面直角坐标系中作出△ABC 关于 y 轴对称
的图形△A1B1C1(点 A 对应点 A1,点 B 对应点 B1,点 C
对应点 C1);
(2)△ABC 的面积= ,点 C 到 AB 的距离= ;
(3)若在 x 轴上有一点 P,使△PBC 周长值最小,此时△PBC
周长最小值为 .
18.(8 分)如图,把一张长方形纸片 ABCD 折叠起来,使其对角顶点 A 与 C 重合,D 与 G
重合.若长方形的长 BC 为 8,宽 AB 为 4,求:
(1)AF 的长;
(2)求阴影部分三角形 GED 的面积.
第 18 题 第 19 题
初二数学 第 3 页/共 4 页
{#{QQABCQeaEs4oggCQggAspTAAACAAA4gKCUU0wVVYICgsEQQskIOBAgLAeAgSEggGQgCBNAuMAsYACIACCJQFIFAKBAC=A}#=}}#}
19.(7 分)细心观察图形,认真分析各式,然后解答下列问题:
, ,(S1 是 Rt△A1A2O 的面积);
, ,(S2 是 Rt△A2A3O 的面积);
, ,(S3 是 Rt△A3A4O 的面积);…
(1)填空: = ,S10= ;
(2)请用含有 n(n 为正整数)的式子填空: = ,Sn= ;
(3)我们已经知道 ,因此将 分子、分母同时乘以
, 分 母 就 变 成 了 4 , 请 仿 照 这 种 方 法 求
的值;
20.(10 分)【问题呈现】“一直线三等角”,是几何证明的常见模型.
(1)如图 1,VABC 和VADE 均为等边三角形,点 D 为BC 边上一个动点,BC 4,点 O
为 AC 边中点,连接CE,写出图中全等的三角形______.线段 AE 的最小值______.
【问题探索】
(2)△ACB是等腰直角三角形, ACB 90 ,CA CB ,点 E 是 AB 上一点,
CED 45 ,交BC 于 D.
①如图①试探究 AE、BE、EC的数量关系,并给予证明;
②如图②,若 AE 2,BE 6,点 F 是 BE 的中点,求CF 的长.
【灵活运用】
(3)如图 3,四边形 ABCD中,对角线 AC、BD 相交于点 E, AB AD ,
BAD ACD 150 , ACB 30 ,AC 8,求四边形 ABCD的面积.
初二数学 第 4 页/共 4 页
{#{QQABCQaeEs4oggCQggAspTAAACAAA4gKCUU0wVVYICgsEQQskIOBAgLAeAgSEggGQgCBNAuMAsYACIACCJQFIFAKBAC=A}#=}}#}
第一学期 10 月集中练习
初二数学
考试范围:第一至第三章 ;考试时间:100 分钟
一.选择题(共 8 小题,共 24 分)
1.下列实数 ,0.3, , , , ,0.1010010001…(相邻两个 1 之间依
次增加一个 0),其中无理数有( )
A.1 个 B.2 个 C.3 个 D.4 个
2.下列运算正确的是( )
A. B. C. D.
3.如图,小明用手盖住的点的坐标可能为( )
第 6 题
A.(3,2) B.(﹣3,2) C.(3,﹣2) D.(﹣3,﹣2)
4. △ABC 中,∠A,∠B,∠C 的对边分别记为 a,b,c,由下列条件不能判定△ABC 为直
角三角形的是( )
A. ∠A+∠B=∠C B. ∠A:∠B:∠C=1:2:3
C. a2 c2 b2 D. a:b:c=4:4:6
5.估计 +1 的值应在( )
A.3 和 4 之间 B.4 和 5 之间 C.5 和 6 之间 D.6 和 7 之间
6.如图所示,正方形 ABGF 和正方形 CDBE 的面积分别是 100 和 36,则以 AD 为直径的半
圆的面积是( )
A.4π B.8π C.12π D.16π
7.数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有
价值的东西,这是数学解题的一个重要原则”.在复习二次根式时,老师提出了一个求代数
式最小值的问题,如: “当0 x 12时,求代数式 2 的最小值”,x 4 12 x 2 16
其中 x2 4 可看作两直角边分别为 x 和 2 的Rt ACP的斜边长, 可看作12 x 2 16
两直角边分别是12 x和 3 的Rt BDP的斜边长.于是构造出如图,将问题转化为求
初二数学 第 1 页/共 4 页
{#{QQABCQaeEs4oggCQggAspTAAACAAA4gKCUU0wVVYICgsEQQskIOBAgLAeAgSEggGQgCBNAuMAsYACIACCJQFIFAKBAC=A}#=}}#}
AP BP 的最小值,运用此方法,请你解决问题:已知 x,y 均为正数,且 x y 2 6 .则
x2 4 y2 16 的最小值是( )
第 7 题 第 8 题
A. 2 5 B.2 11 C.2 15 D.6
8.如图,四边形 ABCD 中,对角线 AC⊥BD,点 F 为 CD 上一点,连接 AF 交 BD 于点 E,
AF⊥AB,DE=DF,∠BAG=∠ABC=45°,BC+AG=20 ,AE=2EF,则 AF=( )
17 2
A.12 B.8 2 C.10 D.
2
二.填空题(共 5 小题,共 15 分)
9. 的平方根是 .
10.比较大小:2 4 ; (填“>”“<”“=”).
11.如图,长方形 ABCD 的边 AB 落在数轴上,A、B 两点在数轴
上对应的数分别为﹣1 和 1,BC=1,连接 BD,以 B 为圆心,BD 为
半径画弧交数轴于点 E,则点 E 在数轴上所表示的数为 .
12.如图,长方体的长为 15,宽为 10,高为 20,点 B 离点 C 的距离
为 5,一只蚂蚁如果要沿着长方体的表面从点 A 爬到点 B,需要爬行的最
短距离是 .
13.如图,在平面直角坐标系中,将△ABO 绕点 A 顺时针旋转到△AB1C1 的
位置,点 B、O 分别落在点 B1、C1 处,点 B1 在 x 轴上,再将△AB1C1 绕点 B1
顺时针旋转到△A1B1C2 的位置,点 C2 在 x 轴上,将△A1B1C2 绕点 C2 顺时针旋
转到△A2B2C2 的位置,点 A2 在 x 轴上,依次进行下去…若点 A( ,0),B(0,2),则
点 A2023 的坐标是 .
初二数学 第 2 页/共 4 页
{#{QQABCQeaEs4oggCQggAspTAAACAAA4gKCUU0wVVYICgsEQQskIOBAgLAeAgSEggGQgCBNAuMAsYACIACCJQFIFAKBAC=A}#=}}#}
三.解答题(共 7 小题,其中第 14 题 15 分,第 15 题 8 分,第 16 题 5 分,第
17 题 8 分,第 18 题 8 分,第 19 题 7 分,第 20 题 10 分,共计 61 分)
14.(1)(6 分)解方程:
①2x2=32; ②8(x﹣1)3=27.
(2)(9 分)计算:
2
① ; ② ( 3 2)( 3 2) 6 ;
3
③ 2023 0 3 1 3 8 12 ;
15.(8 分)已知点 P(a﹣2,2a+8),分别根据下列条件求出点 P 的坐标.
(1)点 P 在 x 轴上;
(2)点 Q 的坐标为(1,5),直线 PQ∥y 轴;
(4)点 P 到 x 轴、y 轴的距离相等.
16.(5 分)在海洋上有一近似于四边形的岛屿,其平面如图①,
小明据此画出该岛的一个数学模型(如图②四边形 ABCD),AC
是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5 千米,
CD= 千米,AD=4 千米.求四边形 ABCD 的面积.
(结果保留根号)
`17.(8 分)如图,已知网格上每个小的正方形的边长为 1
(长度单位),点 A、B、C 在格点上.
(1) 直接在平面直角坐标系中作出△ABC 关于 y 轴对称
的图形△A1B1C1(点 A 对应点 A1,点 B 对应点 B1,点 C
对应点 C1);
(2)△ABC 的面积= ,点 C 到 AB 的距离= ;
(3)若在 x 轴上有一点 P,使△PBC 周长值最小,此时△PBC
周长最小值为 .
18.(8 分)如图,把一张长方形纸片 ABCD 折叠起来,使其对角顶点 A 与 C 重合,D 与 G
重合.若长方形的长 BC 为 8,宽 AB 为 4,求:
(1)AF 的长;
(2)求阴影部分三角形 GED 的面积.
第 18 题 第 19 题
初二数学 第 3 页/共 4 页
{#{QQABCQeaEs4oggCQggAspTAAACAAA4gKCUU0wVVYICgsEQQskIOBAgLAeAgSEggGQgCBNAuMAsYACIACCJQFIFAKBAC=A}#=}}#}
19.(7 分)细心观察图形,认真分析各式,然后解答下列问题:
, ,(S1 是 Rt△A1A2O 的面积);
, ,(S2 是 Rt△A2A3O 的面积);
, ,(S3 是 Rt△A3A4O 的面积);…
(1)填空: = ,S10= ;
(2)请用含有 n(n 为正整数)的式子填空: = ,Sn= ;
(3)我们已经知道 ,因此将 分子、分母同时乘以
, 分 母 就 变 成 了 4 , 请 仿 照 这 种 方 法 求
的值;
20.(10 分)【问题呈现】“一直线三等角”,是几何证明的常见模型.
(1)如图 1,VABC 和VADE 均为等边三角形,点 D 为BC 边上一个动点,BC 4,点 O
为 AC 边中点,连接CE,写出图中全等的三角形______.线段 AE 的最小值______.
【问题探索】
(2)△ACB是等腰直角三角形, ACB 90 ,CA CB ,点 E 是 AB 上一点,
CED 45 ,交BC 于 D.
①如图①试探究 AE、BE、EC的数量关系,并给予证明;
②如图②,若 AE 2,BE 6,点 F 是 BE 的中点,求CF 的长.
【灵活运用】
(3)如图 3,四边形 ABCD中,对角线 AC、BD 相交于点 E, AB AD ,
BAD ACD 150 , ACB 30 ,AC 8,求四边形 ABCD的面积.
初二数学 第 4 页/共 4 页
{#{QQABCQaeEs4oggCQggAspTAAACAAA4gKCUU0wVVYICgsEQQskIOBAgLAeAgSEggGQgCBNAuMAsYACIACCJQFIFAKBAC=A}#=}}#}
同课章节目录
