沪科版数学八年级上册 第11章 平面直角坐标系 综合测试卷(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 第11章 平面直角坐标系 综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 650.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 09:42:44 | ||
图片预览


文档简介
第11 章综合测试卷
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 在平面直角坐标系中,点A(2,-3)位于哪个象限 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 如图,在中国象棋棋盘中,如果将“卒”的位置记作(3,1),那么“相”的位置可记作( )
A.(2,8) B.(2,4)
C.(8,2) D.(4,2)
3. 将点 P向下平移3个单位,向右平移2个单位后,得到点Q(5,-3),则点 P 的坐标为 ( )
A.(7,0) B.(2,1) C.(8,-5) D.(3,0)
4. 在平面直角坐标系中,点A的坐标是(3a-5,a+1).若点A到x轴的距离与到y轴的距离相等,且点A在y轴的右侧,则a的值为( )
A.1 B.2 C.3 D.1或3
5. 定义::f(a,b)=(-a,b),g(m,n)=(m,-n),例如f(1,2)=(-1,2),g(-4,-5)=(-4,5),则g(f(3,-4))的值为 ( )
A.(3,-4) B.(-3,4) C.(3,4) D.( -3,-4)
6. 在直角坐标系中,某三角形三个顶点的横坐标不变,纵坐标都增加2个单位长度,则所得三角形与原三角形相比 ( )
A.形状不变,面积扩大2倍 B.形状不变,位置向上平移2个单位长度
C.形状不变,位置向右平移2个单位长度 D.以上都不对
7. 第二象限内的点P(x,y),满足 则点 P的坐标是 ( )
A.(9,2) B.( -3,2) C.( -9,2) D.( -2,9)
8. 在平面直角坐标系中,点A(1,2)平移后的坐标是A'(-3,3),按照同样的规律平移其他点,则符合这种要求的变换是 ( )
A.(3,2)→(4,-2) B.(-1,0)→(-5,-4)
C.(2,5)→(-1,5) D.(1,5)→( -3,6)
9. 已知三角形ABC内任意一点 P(a,b)经过平移后对应点P (c,d),已知A( ﹣1,2+m)在经过此次平移后对应点A (2,-3+m).则a+b-c-d的值为 ( )
A.8+m B. -8+m C.2 D. -2
10. (百色中考)阅读理解:已知两点M(x ,y ),N(x ,y ),.则线段MN的中点K(x,y)的坐标公式为: 如图,已知点O为坐标原点,点A(-3,0),⊙O经过点A,点B为弦PA的中点.若点P(a,b),则有a,b满足等式: 设B(m,n),则m,n满足的等式是
( )
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 在平面直角坐标系xOy中,点A的坐标为(2,0),动点P的坐标为 若∠POA = 45°,则m的值为 .
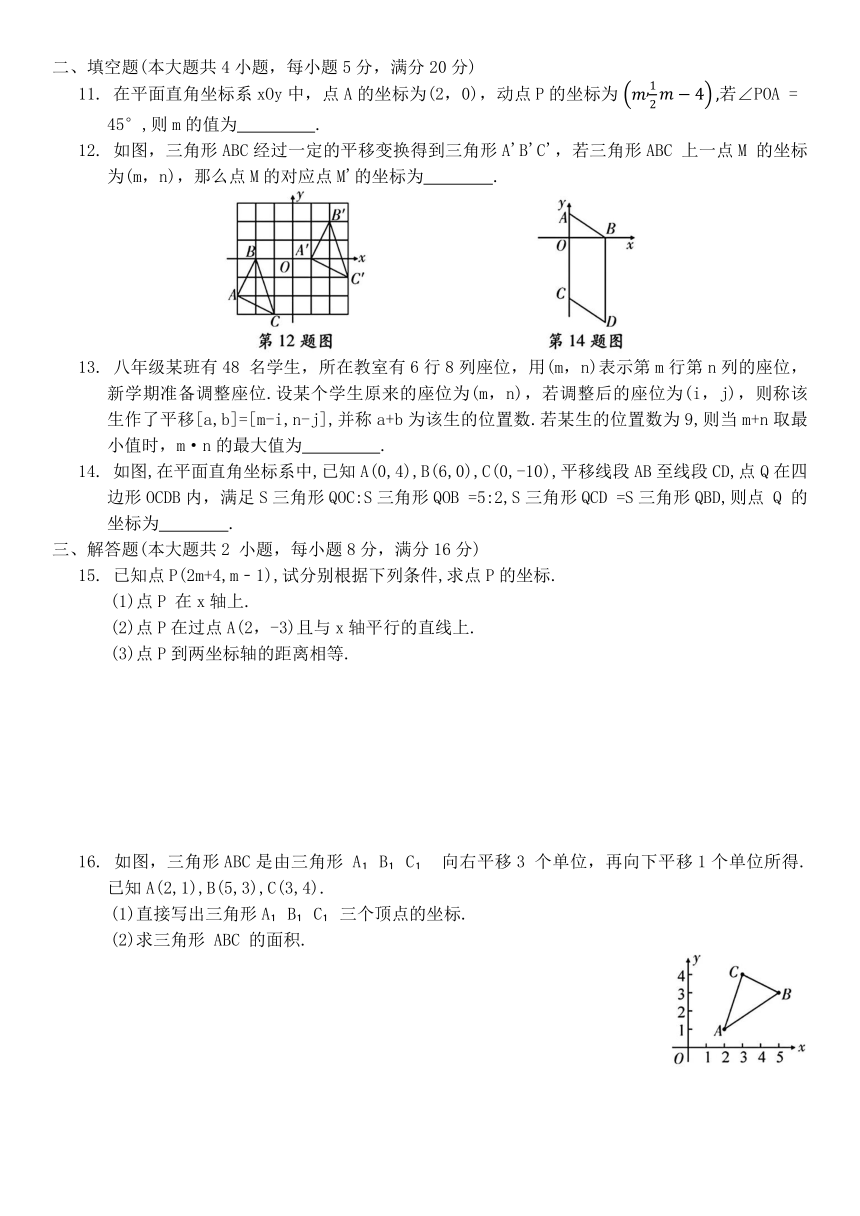
12. 如图,三角形ABC经过一定的平移变换得到三角形A'B'C',若三角形ABC 上一点M 的坐标为(m,n),那么点M的对应点M'的坐标为 .
13. 八年级某班有48 名学生,所在教室有6行8列座位,用(m,n)表示第m行第n列的座位,新学期准备调整座位.设某个学生原来的座位为(m,n),若调整后的座位为(i,j),则称该生作了平移[a,b]=[m-i,n-j],并称a+b为该生的位置数.若某生的位置数为9,则当m+n取最小值时,m·n的最大值为 .
14. 如图,在平面直角坐标系中,已知A(0,4),B(6,0),C(0,-10),平移线段AB至线段CD,点Q在四边形OCDB内,满足S三角形QOC:S三角形QOB =5:2,S三角形QCD =S三角形QBD,则点 Q 的坐标为 .
三、解答题(本大题共2 小题,每小题8分,满分16分)
15. 已知点P(2m+4,m﹣1),试分别根据下列条件,求点P的坐标.
(1)点P 在x轴上.
(2)点P在过点A(2,-3)且与x轴平行的直线上.
(3)点P到两坐标轴的距离相等.
16. 如图,三角形ABC是由三角形 A B C 向右平移3 个单位,再向下平移1个单位所得.已知A(2,1),B(5,3),C(3,4).
(1)直接写出三角形A B C 三个顶点的坐标.
(2)求三角形 ABC 的面积.
四、(本大题共2小题,每小题8分,满分16分)
17. 坐标系中,过点(0,2)的直线a垂直y轴,M(9,2)为直线a上一点,若点P从点M出发,以2cm /s的速度沿直线a向左移动;点Q 从原点同时出发,以1cm/s的速度沿x轴向右移动,多久后线段PQ 平行于y轴
18. 在平面直角坐标系中,有点A(a-1,3),B(a+2,2a-1).
(1)若线段AB∥x轴,求点A,B的坐标.
(2)当点B到y轴的距离与点A到x轴的距离相等时,求点 B所在的象限.
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,三角形A'B'C'是由三角形ABC经过某种平移得到的,点A 与点 ,点B与点B',点C与点 C'分别对应,观察点与点坐标之间的关系,解答下列问题:
(1)分别写出点A,点B,点C,点A',点B',点C'的坐标,并说明三角形. 是由三角形ABC经过怎样的平移得到的.
(2)若点M(a+2,4-b)是点N(2a-3,2b-5)通过(1)中的平移变换得到的,求 的值.
20. 点P是平面直角坐标系中的一点且不在坐标轴上,过点P向x轴、y轴作垂线段,若垂线段的长度和为4,则点P叫做“垂距点”,如图中的点P(1,3)是“垂距点”.
(1)在点 中,是“垂距点”的是点 .
(2)若点 是“垂距点”,求m的值.
六、(本题满分12分)
21. 已知在平面直角坐标系中有三点A(﹣2,1),B(3,1),C(2,3),请回答如下问题:
(1)在平面直角坐标系内描出点A,B,C.
(2)在坐标系内存在点P,使以A,B,C,P四个点组成的四边形中,相对的两边互相平行且相等,则点 P 的坐标为 .(直接写出答案)
(3)平移线段BC,使得C点的对应点刚好与坐标原点重合,求出线段 BC在平移的过程中扫过的面积.
七、(本题满分12分)
22. 如图,在平面直角坐标系中,点A,B的坐标分别为( -1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1 个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC 的面积.
(2)在x轴上是否存在一点 F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点 F 的坐标;若不存在,请说明理由.
八、(本题满分14分)
23. 已知点A在平面直角坐标系中第一象限内,将线段AO平移至线段BC,其中点A 与点 B 对应.
(1)如图1,若A(1,3),B(3,0),连接AB,AC,在坐标轴上存在一点 D,使得 求点 D 的坐标.
(2)如图2,若 ,点P为y轴上一动点(点P不与原点重合),请直接写出. 与∠BCP 之间的数量关系.
参 考 答 案
第11 章综合测试卷
1. D 2. C 3. D 4. C 5. B 6. B 7. C 8. D 9. C 10. D 12.(m+4,n+2) 13.30
15.解:(1)因为点P在x轴上,所以m﹣1=0,解得m=1,所以2m+4=6,所以
P(6,0).
(2)因为点P在过点A(2,-3)且与x轴平行的直线上,所以m-1=-3,解得m=-2,所以2m+4=0,所以.
(3)因为点 P到两坐标轴的距离相等,
①当2m+4=m-1时,m=-5,所以 所以P( -6,-6),
②当2m+4+(m--1)=0时,m=-1,
所以2m+4=2,m-1=-2,所以P(2,-2).
综上所述,当点 P到两坐标轴的距离相等时, 或
16.解:(1)因为三角形ABC是由三角形. 向右平移3个单位,再向下平移1个单位所得,
所以三角形A B C 是由三角形ABC向左平移3个单位,再向上平移1个单位所得,所以
(2)如图,三角形ABC的面积
17.解:设当PQ∥γ轴时,点P的运动时间为x/s.
依题意,有9-2x=x,解得x=3.
故3秒后线段PQ平行于y轴.
18.解:(1)因为线段AB∥x轴,所以 解得 故a-1=1,a+2=4,则A(1,3),B(4,3).
(2)因为点B到y轴的距离与点A到x轴的距离相等,
所以|a+2|=3,解得a=-5或1,
当a=-5时,a+2= -3,2a-1=-11,
故B( -3,-11)在第三象限;
当a=1时,a+2=3,2a-1=1,
故B(3,1)在第一象限,综上所述,点B在第一象限或第三象限.
19.解:(1)由图知,A(0,3),B(2,1),C(3,4),
1,
三角形ABC 向左平移3个单位,向下平移3个单位可以得到三角形.
(2)由(1)中的平移变换,得 解得a=8,b=4,则(
20.解:(1)根据题意,对于点A而言,|-2|+|2|=4,所以点A是“垂距点”,对于点 B而言, 所以点B不是“垂距点”,对于点C而言,l-1|+|5|=6≠4,所以点 C不是“垂距点”,故答案为:A.
(2)由题意,可知
①当m>0时,则4m=4,解得m=1;
②当m<0时,则-4m=4,解得m=-1;所以m=±1.
21. 解:(1)点A,B,C如图所示.
(2)满足条件的点P 的坐标为(7,3)或( -3,3)或( -1,-1).
故答案为:(7,3)或(-3,3)或( -1,-1).
(3)线段BC在平移的过程中扫过的面积
22. 解:(1)C(0,2),D(4,2),S四边形ABDC =AB·OC=4×2=8.
(2)存在,当 时,三角形 DFC的面积是三角形 DFB 面积的2倍.
因为C(0,2),D(4,2),所以 因为 B(3,0),所以F(1,0)或(5,0).
23. 解:(1)因为A(1,3)经过平移得B(3,0),所以点O(0,0)平移后的坐标为C(2,-3),
所以 所以
当点D在y轴上时,三角形AOD的高为1,所以三角形AOD的底为18.
所以D(0,18)或D(0,-18);
当点D在x轴上时,三角形 AOD的高为3.所以三角形 AOD 的底为6,
所以D(6,0)或D( -6,0),
综上所述,点D的坐标为(0,18)或(0,-18)或(6,0)或( -6,0).
(2)∠CPO 与∠BCP 的数量关系是:
∠BCP+∠CPO=30°或∠BCP +∠CPO=120°或∠BCP+∠CPO=150°.
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 在平面直角坐标系中,点A(2,-3)位于哪个象限 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 如图,在中国象棋棋盘中,如果将“卒”的位置记作(3,1),那么“相”的位置可记作( )
A.(2,8) B.(2,4)
C.(8,2) D.(4,2)
3. 将点 P向下平移3个单位,向右平移2个单位后,得到点Q(5,-3),则点 P 的坐标为 ( )
A.(7,0) B.(2,1) C.(8,-5) D.(3,0)
4. 在平面直角坐标系中,点A的坐标是(3a-5,a+1).若点A到x轴的距离与到y轴的距离相等,且点A在y轴的右侧,则a的值为( )
A.1 B.2 C.3 D.1或3
5. 定义::f(a,b)=(-a,b),g(m,n)=(m,-n),例如f(1,2)=(-1,2),g(-4,-5)=(-4,5),则g(f(3,-4))的值为 ( )
A.(3,-4) B.(-3,4) C.(3,4) D.( -3,-4)
6. 在直角坐标系中,某三角形三个顶点的横坐标不变,纵坐标都增加2个单位长度,则所得三角形与原三角形相比 ( )
A.形状不变,面积扩大2倍 B.形状不变,位置向上平移2个单位长度
C.形状不变,位置向右平移2个单位长度 D.以上都不对
7. 第二象限内的点P(x,y),满足 则点 P的坐标是 ( )
A.(9,2) B.( -3,2) C.( -9,2) D.( -2,9)
8. 在平面直角坐标系中,点A(1,2)平移后的坐标是A'(-3,3),按照同样的规律平移其他点,则符合这种要求的变换是 ( )
A.(3,2)→(4,-2) B.(-1,0)→(-5,-4)
C.(2,5)→(-1,5) D.(1,5)→( -3,6)
9. 已知三角形ABC内任意一点 P(a,b)经过平移后对应点P (c,d),已知A( ﹣1,2+m)在经过此次平移后对应点A (2,-3+m).则a+b-c-d的值为 ( )
A.8+m B. -8+m C.2 D. -2
10. (百色中考)阅读理解:已知两点M(x ,y ),N(x ,y ),.则线段MN的中点K(x,y)的坐标公式为: 如图,已知点O为坐标原点,点A(-3,0),⊙O经过点A,点B为弦PA的中点.若点P(a,b),则有a,b满足等式: 设B(m,n),则m,n满足的等式是
( )
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 在平面直角坐标系xOy中,点A的坐标为(2,0),动点P的坐标为 若∠POA = 45°,则m的值为 .
12. 如图,三角形ABC经过一定的平移变换得到三角形A'B'C',若三角形ABC 上一点M 的坐标为(m,n),那么点M的对应点M'的坐标为 .
13. 八年级某班有48 名学生,所在教室有6行8列座位,用(m,n)表示第m行第n列的座位,新学期准备调整座位.设某个学生原来的座位为(m,n),若调整后的座位为(i,j),则称该生作了平移[a,b]=[m-i,n-j],并称a+b为该生的位置数.若某生的位置数为9,则当m+n取最小值时,m·n的最大值为 .
14. 如图,在平面直角坐标系中,已知A(0,4),B(6,0),C(0,-10),平移线段AB至线段CD,点Q在四边形OCDB内,满足S三角形QOC:S三角形QOB =5:2,S三角形QCD =S三角形QBD,则点 Q 的坐标为 .
三、解答题(本大题共2 小题,每小题8分,满分16分)
15. 已知点P(2m+4,m﹣1),试分别根据下列条件,求点P的坐标.
(1)点P 在x轴上.
(2)点P在过点A(2,-3)且与x轴平行的直线上.
(3)点P到两坐标轴的距离相等.
16. 如图,三角形ABC是由三角形 A B C 向右平移3 个单位,再向下平移1个单位所得.已知A(2,1),B(5,3),C(3,4).
(1)直接写出三角形A B C 三个顶点的坐标.
(2)求三角形 ABC 的面积.
四、(本大题共2小题,每小题8分,满分16分)
17. 坐标系中,过点(0,2)的直线a垂直y轴,M(9,2)为直线a上一点,若点P从点M出发,以2cm /s的速度沿直线a向左移动;点Q 从原点同时出发,以1cm/s的速度沿x轴向右移动,多久后线段PQ 平行于y轴
18. 在平面直角坐标系中,有点A(a-1,3),B(a+2,2a-1).
(1)若线段AB∥x轴,求点A,B的坐标.
(2)当点B到y轴的距离与点A到x轴的距离相等时,求点 B所在的象限.
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,三角形A'B'C'是由三角形ABC经过某种平移得到的,点A 与点 ,点B与点B',点C与点 C'分别对应,观察点与点坐标之间的关系,解答下列问题:
(1)分别写出点A,点B,点C,点A',点B',点C'的坐标,并说明三角形. 是由三角形ABC经过怎样的平移得到的.
(2)若点M(a+2,4-b)是点N(2a-3,2b-5)通过(1)中的平移变换得到的,求 的值.
20. 点P是平面直角坐标系中的一点且不在坐标轴上,过点P向x轴、y轴作垂线段,若垂线段的长度和为4,则点P叫做“垂距点”,如图中的点P(1,3)是“垂距点”.
(1)在点 中,是“垂距点”的是点 .
(2)若点 是“垂距点”,求m的值.
六、(本题满分12分)
21. 已知在平面直角坐标系中有三点A(﹣2,1),B(3,1),C(2,3),请回答如下问题:
(1)在平面直角坐标系内描出点A,B,C.
(2)在坐标系内存在点P,使以A,B,C,P四个点组成的四边形中,相对的两边互相平行且相等,则点 P 的坐标为 .(直接写出答案)
(3)平移线段BC,使得C点的对应点刚好与坐标原点重合,求出线段 BC在平移的过程中扫过的面积.
七、(本题满分12分)
22. 如图,在平面直角坐标系中,点A,B的坐标分别为( -1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1 个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC 的面积.
(2)在x轴上是否存在一点 F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点 F 的坐标;若不存在,请说明理由.
八、(本题满分14分)
23. 已知点A在平面直角坐标系中第一象限内,将线段AO平移至线段BC,其中点A 与点 B 对应.
(1)如图1,若A(1,3),B(3,0),连接AB,AC,在坐标轴上存在一点 D,使得 求点 D 的坐标.
(2)如图2,若 ,点P为y轴上一动点(点P不与原点重合),请直接写出. 与∠BCP 之间的数量关系.
参 考 答 案
第11 章综合测试卷
1. D 2. C 3. D 4. C 5. B 6. B 7. C 8. D 9. C 10. D 12.(m+4,n+2) 13.30
15.解:(1)因为点P在x轴上,所以m﹣1=0,解得m=1,所以2m+4=6,所以
P(6,0).
(2)因为点P在过点A(2,-3)且与x轴平行的直线上,所以m-1=-3,解得m=-2,所以2m+4=0,所以.
(3)因为点 P到两坐标轴的距离相等,
①当2m+4=m-1时,m=-5,所以 所以P( -6,-6),
②当2m+4+(m--1)=0时,m=-1,
所以2m+4=2,m-1=-2,所以P(2,-2).
综上所述,当点 P到两坐标轴的距离相等时, 或
16.解:(1)因为三角形ABC是由三角形. 向右平移3个单位,再向下平移1个单位所得,
所以三角形A B C 是由三角形ABC向左平移3个单位,再向上平移1个单位所得,所以
(2)如图,三角形ABC的面积
17.解:设当PQ∥γ轴时,点P的运动时间为x/s.
依题意,有9-2x=x,解得x=3.
故3秒后线段PQ平行于y轴.
18.解:(1)因为线段AB∥x轴,所以 解得 故a-1=1,a+2=4,则A(1,3),B(4,3).
(2)因为点B到y轴的距离与点A到x轴的距离相等,
所以|a+2|=3,解得a=-5或1,
当a=-5时,a+2= -3,2a-1=-11,
故B( -3,-11)在第三象限;
当a=1时,a+2=3,2a-1=1,
故B(3,1)在第一象限,综上所述,点B在第一象限或第三象限.
19.解:(1)由图知,A(0,3),B(2,1),C(3,4),
1,
三角形ABC 向左平移3个单位,向下平移3个单位可以得到三角形.
(2)由(1)中的平移变换,得 解得a=8,b=4,则(
20.解:(1)根据题意,对于点A而言,|-2|+|2|=4,所以点A是“垂距点”,对于点 B而言, 所以点B不是“垂距点”,对于点C而言,l-1|+|5|=6≠4,所以点 C不是“垂距点”,故答案为:A.
(2)由题意,可知
①当m>0时,则4m=4,解得m=1;
②当m<0时,则-4m=4,解得m=-1;所以m=±1.
21. 解:(1)点A,B,C如图所示.
(2)满足条件的点P 的坐标为(7,3)或( -3,3)或( -1,-1).
故答案为:(7,3)或(-3,3)或( -1,-1).
(3)线段BC在平移的过程中扫过的面积
22. 解:(1)C(0,2),D(4,2),S四边形ABDC =AB·OC=4×2=8.
(2)存在,当 时,三角形 DFC的面积是三角形 DFB 面积的2倍.
因为C(0,2),D(4,2),所以 因为 B(3,0),所以F(1,0)或(5,0).
23. 解:(1)因为A(1,3)经过平移得B(3,0),所以点O(0,0)平移后的坐标为C(2,-3),
所以 所以
当点D在y轴上时,三角形AOD的高为1,所以三角形AOD的底为18.
所以D(0,18)或D(0,-18);
当点D在x轴上时,三角形 AOD的高为3.所以三角形 AOD 的底为6,
所以D(6,0)或D( -6,0),
综上所述,点D的坐标为(0,18)或(0,-18)或(6,0)或( -6,0).
(2)∠CPO 与∠BCP 的数量关系是:
∠BCP+∠CPO=30°或∠BCP +∠CPO=120°或∠BCP+∠CPO=150°.
