第13章 轴对称 章节训练2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第13章 轴对称 章节训练2024-2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 619.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 09:46:53 | ||
图片预览


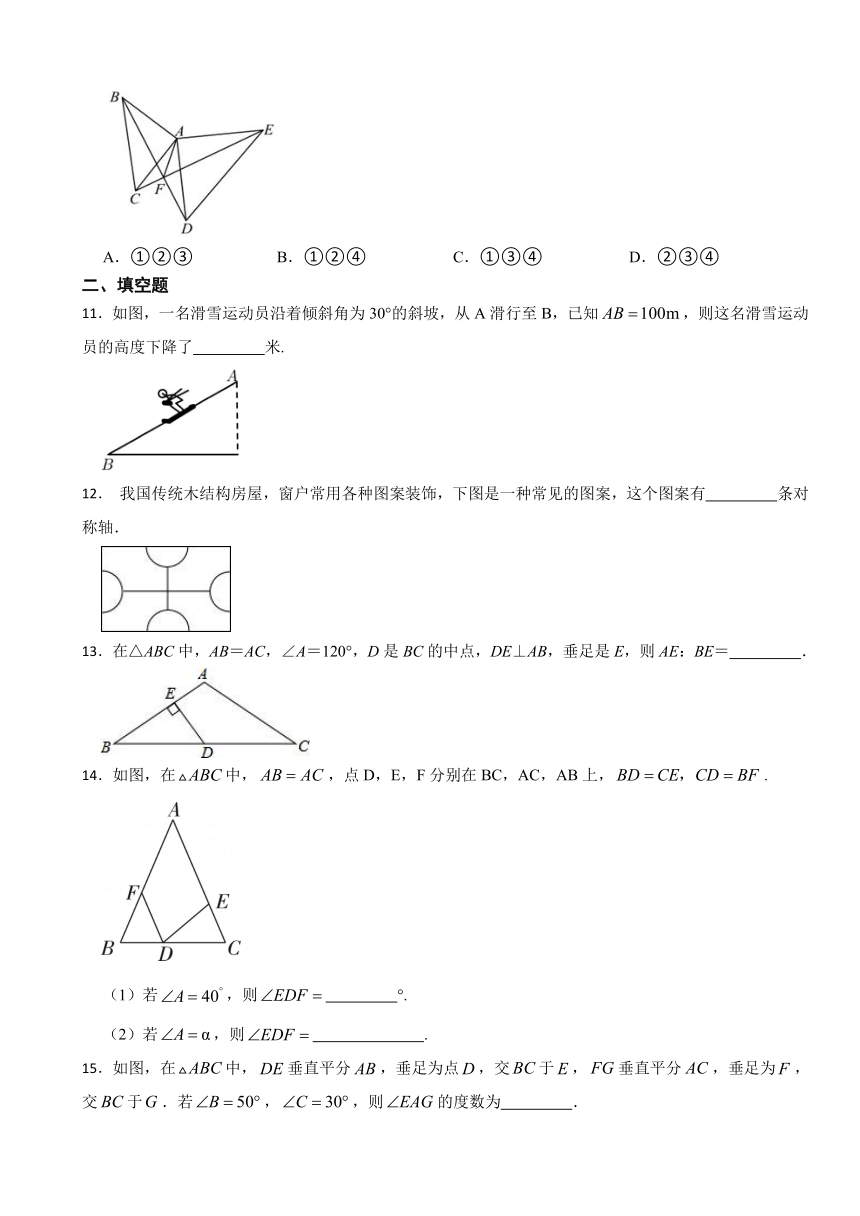

文档简介
第13章 轴对称 章节训练2024-2025学年人教版数学八年级上册
一、单选题
1.点关于x轴的对称点是( )
A. B. C. D.
2.如图,,,则的度数为( )
A. B. C. D.
3.如图,已知,则下列结论错误的是( )
A. B. C. D.
4.如图,在边长为4的等边中,D 是的中点,点E在线段上,连接,在的下方作等边,连接,当最小时,的长度为( ).
A. B.2 C. D.3
5.如图, , 都是等边三角形,则作 的度数是( )
A. B. C. D.
6.等腰三角形的一个角是,它的底角度数为( )
A. B. C.或 D.或
7.如图,在中,的垂直平分线分别交、于点D、E.若的周长为24,,则的周长为( )
A.12 B.14 C.16 D.18
8.如图,在等边中,以为直角顶点作等腰直角, 分别交 、于 点 、, 为线段上一动点,为线段上一动点,且, 以下个结论:①;②;③;④当的值最小时, . 正确的个数为( )
A.4个 B.3 个
C.2 个 D.1 个
9.如图,在中,的平分线交于点D,过点D作,,垂足分别为E,F.下面四个结论:①;②垂直平分;③;④.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
10.如图,已知 △ABC和 △ADE都是等腰三角形,∠BAC=∠DAE=90° ,连结BD,CE交于点F,连结AF,下列结论:① BD=CE;② BF⊥CF;③ AF平分 ∠CAD;④ ∠AFE=45°
其中结论正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
11.如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B,已知,则这名滑雪运动员的高度下降了 米.
12. 我国传统木结构房屋,窗户常用各种图案装饰,下图是一种常见的图案,这个图案有 条对称轴.
13.在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足是E,则AE:BE= .
14.如图,在中,,点D,E,F分别在BC,AC,AB上,.
(1)若,则 °.
(2)若,则 .
15.如图,在中,垂直平分,垂足为点,交于,垂直平分,垂足为,交于.若,,则的度数为 .
16.如图,是等腰三角形,,,在腰上取一点,,垂足为,另一腰上的高交于点,垂足为,若,则的长为 .
17.如图,在中,,,于点D,平分交于点E,交于点G,过点A作于点H,交于点F,下列结论:①;②;③;④,其中正确的序号有 .
18.如图,在等腰中,,,是等边三角形,P是的平分线上一动点,连接,,则的最小值为 .
三、解答题
19.如图,中,,垂直平分,交于点,交于点,且.
(1)若,求的度数;
(2)若周长为,,求长.
20.等腰三角形一腰上的中线把这个三角形的周长分成12和21两部分,求这个等腰三角形的底边长.
21.如图,在中,,点是的中点,点在上,,.
(1)求的度数;
(2)求的度数.
22.在平面直角坐标系中,,,连接交轴于点,,过点作轴的垂线交轴于点.
(1)若点从点出发,沿的边逆时针运动至点,速度每秒个单位长度,运动时间为秒,的面积为,请用含的式子表示;
(2)如图,连接,当向左平移的过程中,轴上是否存在一点,使为等腰直角三角形?若存在,请求出点的坐标,若不存在,请说明理由.
23.小明坐于堤边垂钓,如图①,河堤AC的坡角为30°,AC长米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②).
24.如图,A(6, 0),B(0, 4),点B关于x轴的对称点为C点,点D在x轴的负半轴上,△ABD的面积是30.
(1)求点D坐标.
(2)若动点P从点B出发,沿射线BC运动,速度为每秒1个单位,设P的运动时间为t秒,△APC的面积为S,求S与t的关系式.
(3)在(2)的条件下,同时点Q从D点出发沿x轴正方向以每秒2个单位速度匀速运动,若点R在过A点且平行于y轴的直线上,当△PQR为以PQ为直角边的等腰直角三角形时,求满足条件的t值,并直接写出点R的坐标.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】A
9.【答案】B
10.【答案】B
11.【答案】50
12.【答案】2
13.【答案】1:3
14.【答案】(1)70
(2)
15.【答案】
16.【答案】6
17.【答案】①③④
18.【答案】20
19.【答案】(1)
(2)4cm
20.【答案】5
21.【答案】(1)
(2)
22.【答案】(1);
(2)或或.
23.【答案】解:延长OA交BC于点D
∵AO的倾斜角是,
∴
∵
在Rt△ACD中, (米),
∴CD=2AD=3米,
又
∴△BOD是等边三角形,
∴(米),
∴BC=BD CD=4.5 3=1.5(米)
答:浮漂B与河堤下端C之间的距离为1.5米
24.【答案】(1)(-9,0);(2)当0<t≤8时,S=×(8-t)×6=-3t+24;当t>8时,S=×(t-8)×6=3t-24;(3)t=10秒或11秒时,△PQR是等腰直角三角形.
一、单选题
1.点关于x轴的对称点是( )
A. B. C. D.
2.如图,,,则的度数为( )
A. B. C. D.
3.如图,已知,则下列结论错误的是( )
A. B. C. D.
4.如图,在边长为4的等边中,D 是的中点,点E在线段上,连接,在的下方作等边,连接,当最小时,的长度为( ).
A. B.2 C. D.3
5.如图, , 都是等边三角形,则作 的度数是( )
A. B. C. D.
6.等腰三角形的一个角是,它的底角度数为( )
A. B. C.或 D.或
7.如图,在中,的垂直平分线分别交、于点D、E.若的周长为24,,则的周长为( )
A.12 B.14 C.16 D.18
8.如图,在等边中,以为直角顶点作等腰直角, 分别交 、于 点 、, 为线段上一动点,为线段上一动点,且, 以下个结论:①;②;③;④当的值最小时, . 正确的个数为( )
A.4个 B.3 个
C.2 个 D.1 个
9.如图,在中,的平分线交于点D,过点D作,,垂足分别为E,F.下面四个结论:①;②垂直平分;③;④.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
10.如图,已知 △ABC和 △ADE都是等腰三角形,∠BAC=∠DAE=90° ,连结BD,CE交于点F,连结AF,下列结论:① BD=CE;② BF⊥CF;③ AF平分 ∠CAD;④ ∠AFE=45°
其中结论正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
11.如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B,已知,则这名滑雪运动员的高度下降了 米.
12. 我国传统木结构房屋,窗户常用各种图案装饰,下图是一种常见的图案,这个图案有 条对称轴.
13.在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足是E,则AE:BE= .
14.如图,在中,,点D,E,F分别在BC,AC,AB上,.
(1)若,则 °.
(2)若,则 .
15.如图,在中,垂直平分,垂足为点,交于,垂直平分,垂足为,交于.若,,则的度数为 .
16.如图,是等腰三角形,,,在腰上取一点,,垂足为,另一腰上的高交于点,垂足为,若,则的长为 .
17.如图,在中,,,于点D,平分交于点E,交于点G,过点A作于点H,交于点F,下列结论:①;②;③;④,其中正确的序号有 .
18.如图,在等腰中,,,是等边三角形,P是的平分线上一动点,连接,,则的最小值为 .
三、解答题
19.如图,中,,垂直平分,交于点,交于点,且.
(1)若,求的度数;
(2)若周长为,,求长.
20.等腰三角形一腰上的中线把这个三角形的周长分成12和21两部分,求这个等腰三角形的底边长.
21.如图,在中,,点是的中点,点在上,,.
(1)求的度数;
(2)求的度数.
22.在平面直角坐标系中,,,连接交轴于点,,过点作轴的垂线交轴于点.
(1)若点从点出发,沿的边逆时针运动至点,速度每秒个单位长度,运动时间为秒,的面积为,请用含的式子表示;
(2)如图,连接,当向左平移的过程中,轴上是否存在一点,使为等腰直角三角形?若存在,请求出点的坐标,若不存在,请说明理由.
23.小明坐于堤边垂钓,如图①,河堤AC的坡角为30°,AC长米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②).
24.如图,A(6, 0),B(0, 4),点B关于x轴的对称点为C点,点D在x轴的负半轴上,△ABD的面积是30.
(1)求点D坐标.
(2)若动点P从点B出发,沿射线BC运动,速度为每秒1个单位,设P的运动时间为t秒,△APC的面积为S,求S与t的关系式.
(3)在(2)的条件下,同时点Q从D点出发沿x轴正方向以每秒2个单位速度匀速运动,若点R在过A点且平行于y轴的直线上,当△PQR为以PQ为直角边的等腰直角三角形时,求满足条件的t值,并直接写出点R的坐标.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】A
9.【答案】B
10.【答案】B
11.【答案】50
12.【答案】2
13.【答案】1:3
14.【答案】(1)70
(2)
15.【答案】
16.【答案】6
17.【答案】①③④
18.【答案】20
19.【答案】(1)
(2)4cm
20.【答案】5
21.【答案】(1)
(2)
22.【答案】(1);
(2)或或.
23.【答案】解:延长OA交BC于点D
∵AO的倾斜角是,
∴
∵
在Rt△ACD中, (米),
∴CD=2AD=3米,
又
∴△BOD是等边三角形,
∴(米),
∴BC=BD CD=4.5 3=1.5(米)
答:浮漂B与河堤下端C之间的距离为1.5米
24.【答案】(1)(-9,0);(2)当0<t≤8时,S=×(8-t)×6=-3t+24;当t>8时,S=×(t-8)×6=3t-24;(3)t=10秒或11秒时,△PQR是等腰直角三角形.
