第12章 全等三角形 章节训练2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第12章 全等三角形 章节训练2024-2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 620.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 09:47:38 | ||
图片预览


文档简介
第12章 全等三角形 章节训练2024-2025学年人教版数学八年级上册
一、单选题
1.如图,,若,,.则( )
A. B. C. D.
2.如图,AB⊥BC于点B,AD⊥DC于点D,若CB=CD,且∠1=30°,则∠BAD的度数是( )
A.90° B.60° C.30° D.15°
3.如图,、、、四点在一条直线上,,,再添一个条件仍不能证明的是( )
A. B. C. D.
4.如图,在△ABC中,P、Q分别是BC、AC上的点,作PD⊥AB,PE⊥AC,垂足分别为D、E,若AQ=PQ,PD=PE,则下列结论:①AE=AD;②∠B=∠C;③∠BAP=∠CAP;④△ABP≌△ACP.其中正确的有( )
A.①② B.①③ C.①②④ D.①③④
5.如图,在和中,,,添加一个条件后,你无法判定的是( )
A. B. C. D.
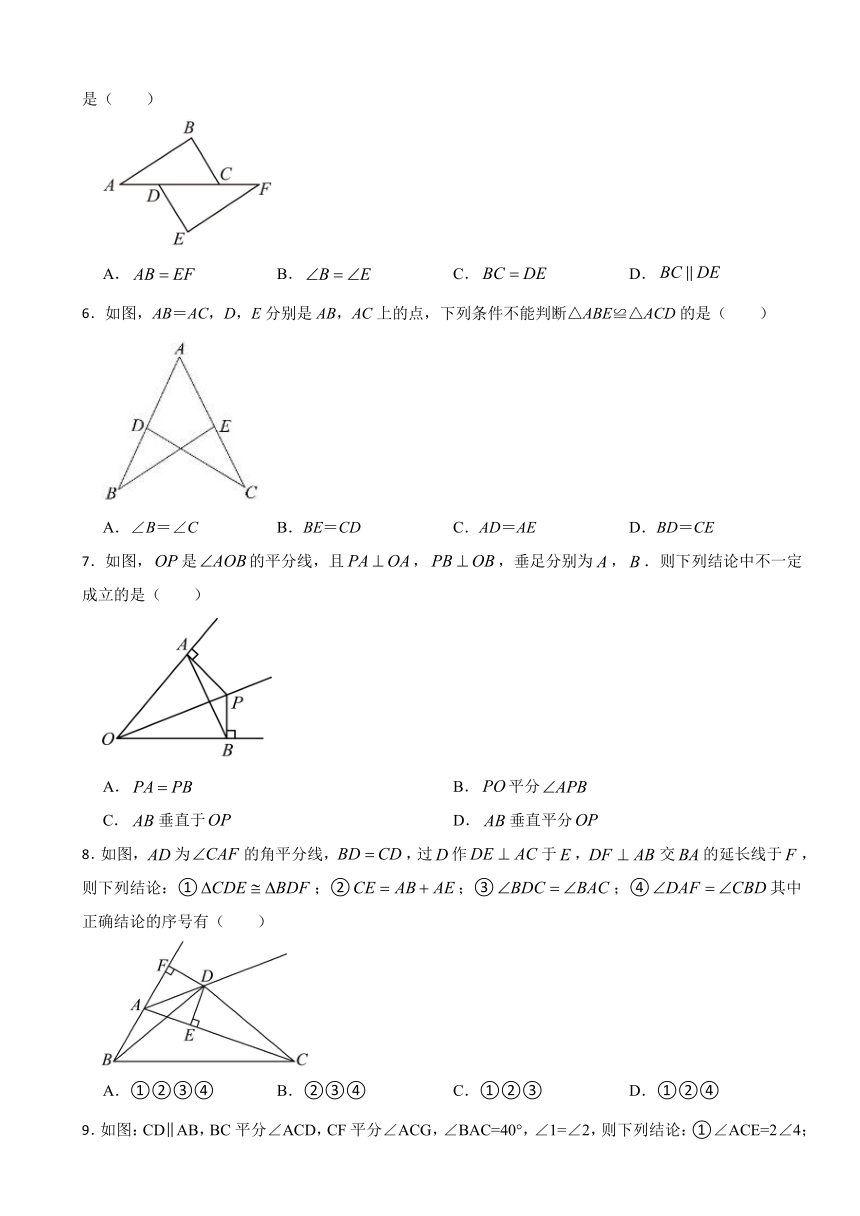
6.如图,AB=AC,D,E分别是AB,AC上的点,下列条件不能判断△ABE≌△ACD的是( )
A.∠B=∠C B.BE=CD C.AD=AE D.BD=CE
7.如图,是的平分线,且,,垂足分别为,.则下列结论中不一定成立的是( )
A. B.平分
C.垂直于 D.垂直平分
8.如图,为的角平分线,,过作于,交的延长线于,则下列结论:①;②;③;④其中正确结论的序号有( )
A.①②③④ B.②③④ C.①②③ D.①②④
9.如图:CDAB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:①∠ACE=2∠4;②CB⊥CF;③∠1=70°;④∠3=2∠4,其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
10.如图,中,.分别以、、为边在的同侧作正方形、、.四块阴影部分的面积如图所示分别记为、、、若,则等于( )
A.10 B.15 C.20 D.30
二、填空题
11.“两条直角边分别对应相等的两个直角三角形全等”是 命题(填“真”或“假”).
12.如图.在中,,.以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于长为半径作弧,在内两弧相交于点P;作射线AP交BC于点F,过点F作,垂足用G.若,则的周长等于 cm.
13.如图,在中,,AD是的平分线,延长AD至点E,使,连接BE,若的面积为9.则的面积是 .
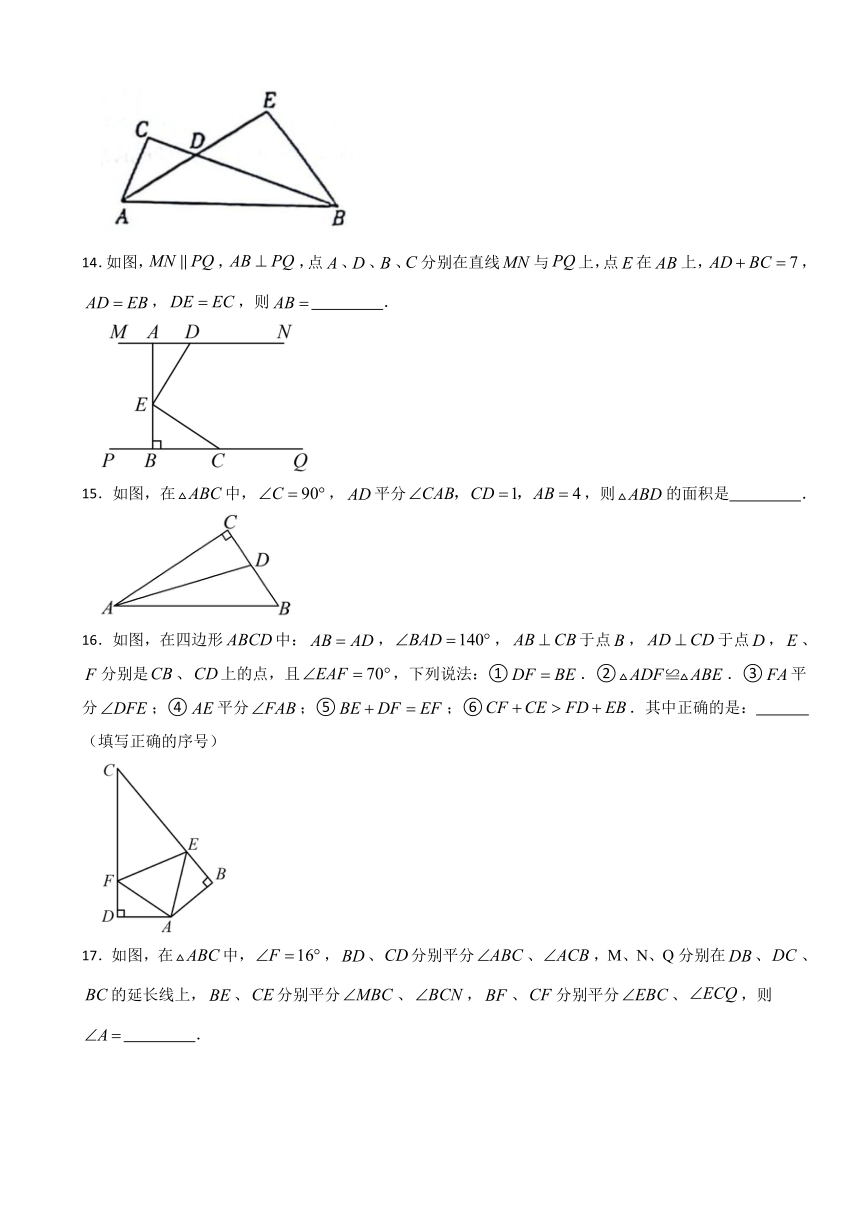
14.如图,,,点、、、分别在直线与上,点在上,,,,则 .
15.如图,在中,,平分,则的面积是 .
16.如图,在四边形中:,,于点,于点,、分别是、上的点,且,下列说法:①.②.③平分;④平分;⑤;⑥.其中正确的是: (填写正确的序号)
17.如图,在中,,、分别平分、,M、N、Q分别在、、的延长线上,、分别平分、,、分别平分、,则 .
三、解答题
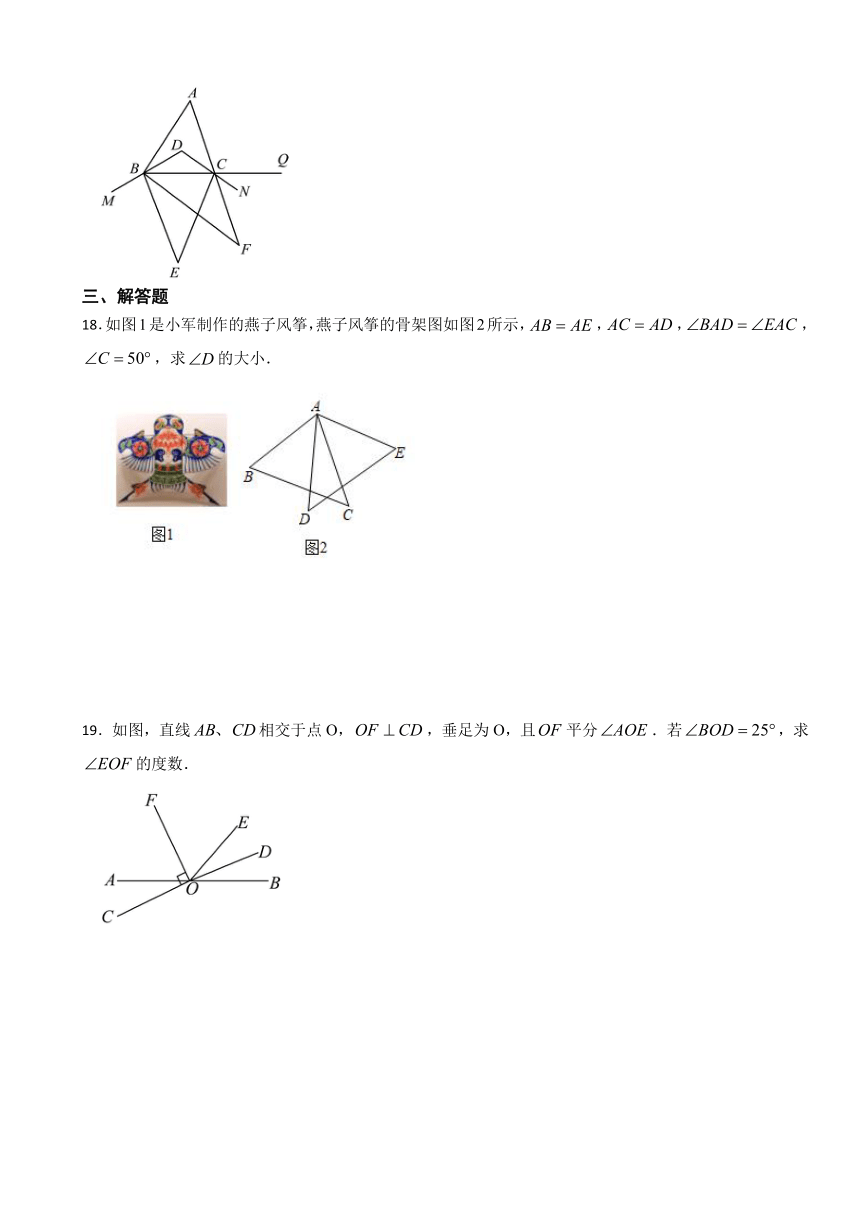
18.如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,,,,,求的大小.
19.如图,直线相交于点O,,垂足为O,且平分.若,求的度数.
20.如图,在中,,的外角的平分线交的延长线于点E.
(1)求的度数;
(2)过点D作,交的延长线于点F,求的度数.
21.如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼AB的高度,首先他们在两栋单元楼之间选定一点E,然后小华在自己家阳台C处测得E处的俯角为∠1,小明站在E处测得楼顶A的仰角为∠2,发现∠1与∠2互余,过点F作FG⊥AB于点G,已知BG=1米,BE=CD=20米,BD=58米,点B、E、D在一条直线上,AB⊥BD,FE⊥BD,CD⊥BD,试求单元楼AB的高.(注:BE=FG,BG=EF,∠1与∠3互余)
22.如图,A,B两点分别位于一个池塘的两端,小明通过构造△ABC与△BCD来测量A,B间的距离,其中,.那么量出的BD的长度就是AB的距离.请你判断小明这个方法正确与否,并给出相应理由.
23.定义:在一个三角形中,如果一个内角的度数比另一个内角度数大,那么这样的三角形我们称为“似黄金三角形”,其中称为“黄金角”.例如:一个三角形三个内角的度数分别是,这个三角形就是“似黄金三角形”,其中为“黄金角”.
(1)一个“似黄金三角形”的一个内角为,若“黄金角”为锐角,则这个“黄金角”的度数为______.
(2)如图,在中,,,为线段上一点(点不与点、点重合).若是“似黄金三角形”,求的度数.
(3)如图,中,点在边上,平分交于点,过点作交于点,且.若和都是“似黄金三角形”,直接写出的度数.
24.如图,AD是的中线,,垂足为E,,交AD的延长线于点F,G是DA延长线上一点,连接BG.
(1)求证:;
(2)若,求证:.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】C
11.【答案】真
12.【答案】8
13.【答案】12
14.【答案】7
15.【答案】2
16.【答案】③⑤⑥
17.【答案】52°
18.【答案】
19.【答案】65°
20.【答案】(1)
(2)
21.【答案】解:∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
∵CD⊥BD, FG⊥AB ,
∴∠AGF=∠CDE=90°,
∵GF=BE, BE=CD ,
∴GF=CD,
在△AGF和△EDC中,
,
∴△AGF≌△EDC(ASA),
∴AG=ED,
∵ED=BD-BE=58-20=38(米),
∴AG=ED=38米,
∴AB=AG+GB=38+1=39(米),
答:单元楼AB的高为39米.
22.【答案】解:根据题意,在和中
∴≌
∴
∴小明这个方法正确.
23.【答案】(1);
(2)或;
(3)或.
24.【答案】(1)证明:∵AD是的中线,
∴,
∵,,
∴,
在和中,
,
∴,
∴
(2)证明:在和中,
,
∴,
∴,
∴,
∵,
∴,
∴.
一、单选题
1.如图,,若,,.则( )
A. B. C. D.
2.如图,AB⊥BC于点B,AD⊥DC于点D,若CB=CD,且∠1=30°,则∠BAD的度数是( )
A.90° B.60° C.30° D.15°
3.如图,、、、四点在一条直线上,,,再添一个条件仍不能证明的是( )
A. B. C. D.
4.如图,在△ABC中,P、Q分别是BC、AC上的点,作PD⊥AB,PE⊥AC,垂足分别为D、E,若AQ=PQ,PD=PE,则下列结论:①AE=AD;②∠B=∠C;③∠BAP=∠CAP;④△ABP≌△ACP.其中正确的有( )
A.①② B.①③ C.①②④ D.①③④
5.如图,在和中,,,添加一个条件后,你无法判定的是( )
A. B. C. D.
6.如图,AB=AC,D,E分别是AB,AC上的点,下列条件不能判断△ABE≌△ACD的是( )
A.∠B=∠C B.BE=CD C.AD=AE D.BD=CE
7.如图,是的平分线,且,,垂足分别为,.则下列结论中不一定成立的是( )
A. B.平分
C.垂直于 D.垂直平分
8.如图,为的角平分线,,过作于,交的延长线于,则下列结论:①;②;③;④其中正确结论的序号有( )
A.①②③④ B.②③④ C.①②③ D.①②④
9.如图:CDAB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:①∠ACE=2∠4;②CB⊥CF;③∠1=70°;④∠3=2∠4,其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
10.如图,中,.分别以、、为边在的同侧作正方形、、.四块阴影部分的面积如图所示分别记为、、、若,则等于( )
A.10 B.15 C.20 D.30
二、填空题
11.“两条直角边分别对应相等的两个直角三角形全等”是 命题(填“真”或“假”).
12.如图.在中,,.以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于长为半径作弧,在内两弧相交于点P;作射线AP交BC于点F,过点F作,垂足用G.若,则的周长等于 cm.
13.如图,在中,,AD是的平分线,延长AD至点E,使,连接BE,若的面积为9.则的面积是 .
14.如图,,,点、、、分别在直线与上,点在上,,,,则 .
15.如图,在中,,平分,则的面积是 .
16.如图,在四边形中:,,于点,于点,、分别是、上的点,且,下列说法:①.②.③平分;④平分;⑤;⑥.其中正确的是: (填写正确的序号)
17.如图,在中,,、分别平分、,M、N、Q分别在、、的延长线上,、分别平分、,、分别平分、,则 .
三、解答题
18.如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,,,,,求的大小.
19.如图,直线相交于点O,,垂足为O,且平分.若,求的度数.
20.如图,在中,,的外角的平分线交的延长线于点E.
(1)求的度数;
(2)过点D作,交的延长线于点F,求的度数.
21.如图,小明和小华住在同一个小区不同单元楼,他们想要测量小明家所在单元楼AB的高度,首先他们在两栋单元楼之间选定一点E,然后小华在自己家阳台C处测得E处的俯角为∠1,小明站在E处测得楼顶A的仰角为∠2,发现∠1与∠2互余,过点F作FG⊥AB于点G,已知BG=1米,BE=CD=20米,BD=58米,点B、E、D在一条直线上,AB⊥BD,FE⊥BD,CD⊥BD,试求单元楼AB的高.(注:BE=FG,BG=EF,∠1与∠3互余)
22.如图,A,B两点分别位于一个池塘的两端,小明通过构造△ABC与△BCD来测量A,B间的距离,其中,.那么量出的BD的长度就是AB的距离.请你判断小明这个方法正确与否,并给出相应理由.
23.定义:在一个三角形中,如果一个内角的度数比另一个内角度数大,那么这样的三角形我们称为“似黄金三角形”,其中称为“黄金角”.例如:一个三角形三个内角的度数分别是,这个三角形就是“似黄金三角形”,其中为“黄金角”.
(1)一个“似黄金三角形”的一个内角为,若“黄金角”为锐角,则这个“黄金角”的度数为______.
(2)如图,在中,,,为线段上一点(点不与点、点重合).若是“似黄金三角形”,求的度数.
(3)如图,中,点在边上,平分交于点,过点作交于点,且.若和都是“似黄金三角形”,直接写出的度数.
24.如图,AD是的中线,,垂足为E,,交AD的延长线于点F,G是DA延长线上一点,连接BG.
(1)求证:;
(2)若,求证:.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】C
11.【答案】真
12.【答案】8
13.【答案】12
14.【答案】7
15.【答案】2
16.【答案】③⑤⑥
17.【答案】52°
18.【答案】
19.【答案】65°
20.【答案】(1)
(2)
21.【答案】解:∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
∵CD⊥BD, FG⊥AB ,
∴∠AGF=∠CDE=90°,
∵GF=BE, BE=CD ,
∴GF=CD,
在△AGF和△EDC中,
,
∴△AGF≌△EDC(ASA),
∴AG=ED,
∵ED=BD-BE=58-20=38(米),
∴AG=ED=38米,
∴AB=AG+GB=38+1=39(米),
答:单元楼AB的高为39米.
22.【答案】解:根据题意,在和中
∴≌
∴
∴小明这个方法正确.
23.【答案】(1);
(2)或;
(3)或.
24.【答案】(1)证明:∵AD是的中线,
∴,
∵,,
∴,
在和中,
,
∴,
∴
(2)证明:在和中,
,
∴,
∴,
∴,
∵,
∴,
∴.
