北京市一六六中学2024~2025学年第一学期初二年级数学十月学业水平测量(无答案)
文档属性
| 名称 | 北京市一六六中学2024~2025学年第一学期初二年级数学十月学业水平测量(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 468.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 09:51:26 | ||
图片预览


文档简介
初二年级数学十月学业水平测量(2024.10.8)
班级: 姓名: 学号:
一、选择题(共24分,每小题2分)
1.中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录.下列四幅作品分别代表“立春”、“谷雨”、“立夏”、“小满”,其中是轴对称图形的是( )
A. B. C. D.
2.下列长度的三条线段,能组成三角形的是( )
A.3,4,5 B.2,5,8 C.5,5,10 D.1,6,7
3.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A、C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是( )
A. SSS B. SAS C. ASA D. AAS
4.已知图中的两个三角形全等,则∠1等于( )
A.72° B.60° C.50° D.58°
5.若一个多边形的内角和等于1800°,这个多边形的边数是( )
A.6 B.8 C.10 D.12
6.用一条长为18cm的细绳围成一个等腰三角形,若其中有一边的长为5cm,则该等腰三角形的腰长为( )cm.
A. 5 B. 6.5 C. 5或6.5 D. 6.5或8
7. 如图,DE是△ABC中AC边的垂直平分线,若BC=6厘米,AB=10厘米,则△EBC的周长为( )
A . 14厘米 B. 16厘米 C. 24厘米 D. 26厘米
第3题 第4题 第7题
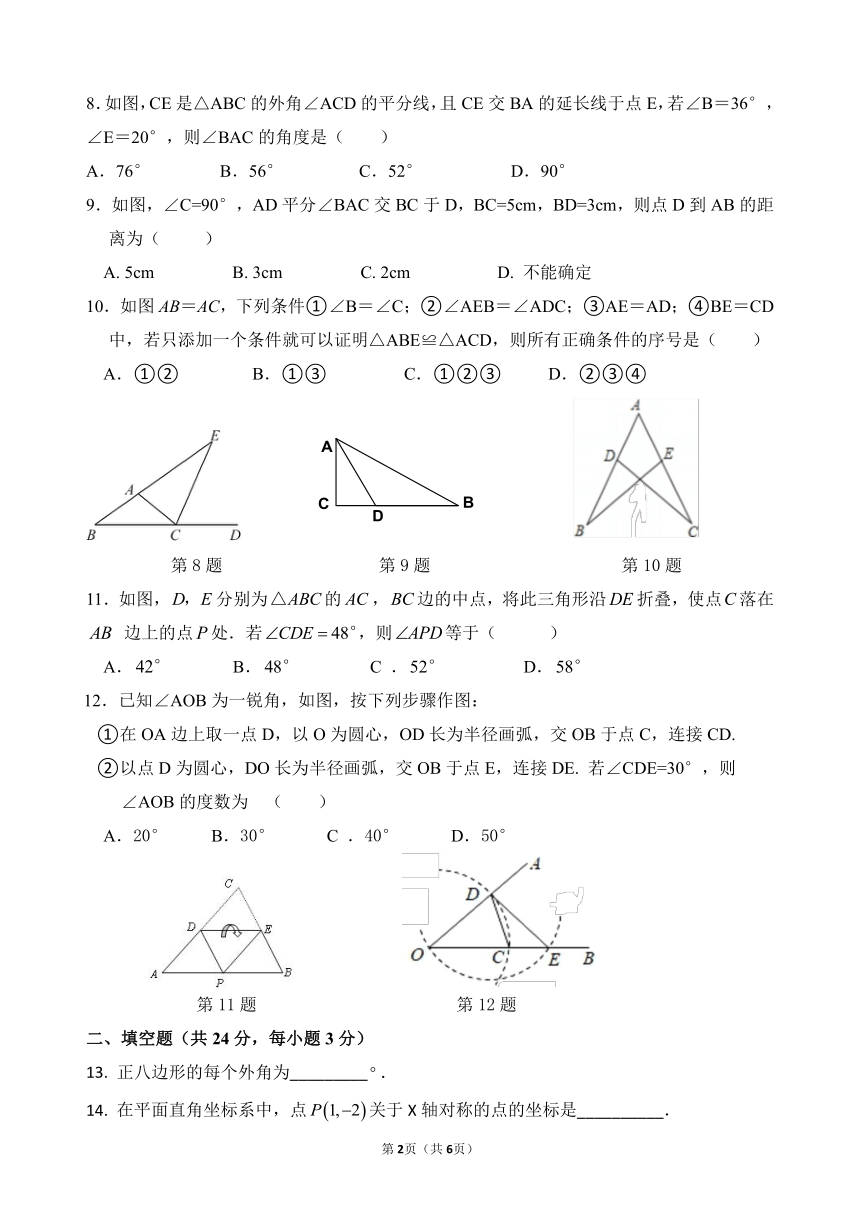
8.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,若∠B=36°,
∠E=20°,则∠BAC的角度是( )
A.76° B.56° C.52° D.90°
9.如图,∠C=90°,AD平分∠BAC交BC于D,BC=5cm,BD=3cm,则点D到AB的距离为( )
A. 5cm B. 3cm C. 2cm D. 不能确定
10.如图AB=AC,下列条件①∠B=∠C;②∠AEB=∠ADC;③AE=AD;④BE=CD中,若只添加一个条件就可以证明△ABE≌△ACD,则所有正确条件的序号是( )
A.①② B.①③ C.①②③ D.②③④
第8题 第9题 第10题
11.如图,分别为的,边的中点,将此三角形沿折叠,使点落在 边上的点处.若,则等于( )
A. B. C . D.
12.已知∠AOB为一锐角,如图,按下列步骤作图:
①在OA边上取一点D,以O为圆心,OD长为半径画弧,交OB于点C,连接CD.
②以点D为圆心,DO长为半径画弧,交OB于点E,连接DE. 若∠CDE=30°,则
∠AOB的度数为 ( )
A.20° B.30° C .40° D.50°
第11题 第12题
二、填空题(共24分,每小题3分)
13. 正八边形的每个外角为_________.
14. 在平面直角坐标系中,点关于X轴对称的点的坐标是__________.
15.已知:如图,AB平分∠CAD.请添加一个
条件 ,使得△ABC≌△ABD.
(要求:不添加辅助线,只需填一个答案即可).
16.等腰三角形的一个角是 40°,则等腰三角形的一个底角是 .
17.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上.若想知道两点A,B的距离,只需要测量出线段 即可.
18.如图,EC与DA交于点B,∠ACB=90°,∠A=60°,BD=BE,则∠DEB的度数是 .
19.如图,已知CB⊥AD,AE⊥CD,垂足分别为B,E, AE、BC相交于点F,若AB=BC=8,CF=2,连接DF,则△CDF的面积是 .
第17题 第18题 第19题
20.在平面直角坐标系中,点A(1,2),B(5,5),C(5,2).如果存在点E,使△ACE和△ACB全等,请写出所有满足条件的E点的坐标 .
三、解答题(共52分,第21-23题每小题5分,第24-26题每小题6分,第28-29题每题7分)
21.(1)解方程组: (2)不等式组:
22.在△ABC中,AD平分∠BAC,交BC于点D,P为线段AD上的 一个动点,
PE⊥AD交直线BC于点E.若∠B=35°,∠ACB=85°.
(1)求∠DAC的度数;
(2)求∠E的度数
23.如图,AB⊥CB,DC⊥CB,E、F在BC上,∠A=∠D,BE=CF,求证:AF=DE.
在平面直角坐标系中,△ABC的顶点坐标分别为A(5,2),B(3,5),C(-1,-1),
画出△ABC关于y轴对称的△ ;
分别写出 、 、 的坐标;
求△ 的面积.
25. 如图,与中,与交于点E,且,.
(1)求证:;
(2)当,求的度数.
26. 如图,四边形ABCD中,AB=AC,∠D=90°,BE⊥AC于点F,交CD于点E,连接EA,EA平分∠DEF.
(1)求证:AF=AD;
(2)若BF=7, DE=3,求CE的长.
如图,等腰中,.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法).
①作的角平分线交于点D;
②在边的延长线上作一点E,使,连接.
在(1)所作的图形中,猜想线段与的数量关系,并证明.
28.如图1,在△ABC中,∠A=60°,BD,CE是△ABC的两条角平分线,且BD,CE交于点F.用等式表示BE,BC,CD这三条线段之间的数量关系,并证明你的结论.
图1 图2
小东通过观察、实验,提出猜想:BE+CD=BC.他发现先在BC上截取BM,使BM=BE,连接FM,如图2,再利用三角形全等的判定和性质证明CM=CD即可.
(1)下面是小东证明该猜想的部分思路,请补充完整:
①在BC上截取BM,使BM=BE,连接FM,则可以证明△BEF与___________全等,判定它们全等的依据是______________;
②由∠A=60°,BD,CE是△ABC的两条角平分线,可以得出∠EFB=______°;
(2)请直接利用①、②已得到的结论,完成证明猜想BE+CD=BC的过程.
第1页(共6页)
班级: 姓名: 学号:
一、选择题(共24分,每小题2分)
1.中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录.下列四幅作品分别代表“立春”、“谷雨”、“立夏”、“小满”,其中是轴对称图形的是( )
A. B. C. D.
2.下列长度的三条线段,能组成三角形的是( )
A.3,4,5 B.2,5,8 C.5,5,10 D.1,6,7
3.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A、C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是( )
A. SSS B. SAS C. ASA D. AAS
4.已知图中的两个三角形全等,则∠1等于( )
A.72° B.60° C.50° D.58°
5.若一个多边形的内角和等于1800°,这个多边形的边数是( )
A.6 B.8 C.10 D.12
6.用一条长为18cm的细绳围成一个等腰三角形,若其中有一边的长为5cm,则该等腰三角形的腰长为( )cm.
A. 5 B. 6.5 C. 5或6.5 D. 6.5或8
7. 如图,DE是△ABC中AC边的垂直平分线,若BC=6厘米,AB=10厘米,则△EBC的周长为( )
A . 14厘米 B. 16厘米 C. 24厘米 D. 26厘米
第3题 第4题 第7题
8.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,若∠B=36°,
∠E=20°,则∠BAC的角度是( )
A.76° B.56° C.52° D.90°
9.如图,∠C=90°,AD平分∠BAC交BC于D,BC=5cm,BD=3cm,则点D到AB的距离为( )
A. 5cm B. 3cm C. 2cm D. 不能确定
10.如图AB=AC,下列条件①∠B=∠C;②∠AEB=∠ADC;③AE=AD;④BE=CD中,若只添加一个条件就可以证明△ABE≌△ACD,则所有正确条件的序号是( )
A.①② B.①③ C.①②③ D.②③④
第8题 第9题 第10题
11.如图,分别为的,边的中点,将此三角形沿折叠,使点落在 边上的点处.若,则等于( )
A. B. C . D.
12.已知∠AOB为一锐角,如图,按下列步骤作图:
①在OA边上取一点D,以O为圆心,OD长为半径画弧,交OB于点C,连接CD.
②以点D为圆心,DO长为半径画弧,交OB于点E,连接DE. 若∠CDE=30°,则
∠AOB的度数为 ( )
A.20° B.30° C .40° D.50°
第11题 第12题
二、填空题(共24分,每小题3分)
13. 正八边形的每个外角为_________.
14. 在平面直角坐标系中,点关于X轴对称的点的坐标是__________.
15.已知:如图,AB平分∠CAD.请添加一个
条件 ,使得△ABC≌△ABD.
(要求:不添加辅助线,只需填一个答案即可).
16.等腰三角形的一个角是 40°,则等腰三角形的一个底角是 .
17.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上.若想知道两点A,B的距离,只需要测量出线段 即可.
18.如图,EC与DA交于点B,∠ACB=90°,∠A=60°,BD=BE,则∠DEB的度数是 .
19.如图,已知CB⊥AD,AE⊥CD,垂足分别为B,E, AE、BC相交于点F,若AB=BC=8,CF=2,连接DF,则△CDF的面积是 .
第17题 第18题 第19题
20.在平面直角坐标系中,点A(1,2),B(5,5),C(5,2).如果存在点E,使△ACE和△ACB全等,请写出所有满足条件的E点的坐标 .
三、解答题(共52分,第21-23题每小题5分,第24-26题每小题6分,第28-29题每题7分)
21.(1)解方程组: (2)不等式组:
22.在△ABC中,AD平分∠BAC,交BC于点D,P为线段AD上的 一个动点,
PE⊥AD交直线BC于点E.若∠B=35°,∠ACB=85°.
(1)求∠DAC的度数;
(2)求∠E的度数
23.如图,AB⊥CB,DC⊥CB,E、F在BC上,∠A=∠D,BE=CF,求证:AF=DE.
在平面直角坐标系中,△ABC的顶点坐标分别为A(5,2),B(3,5),C(-1,-1),
画出△ABC关于y轴对称的△ ;
分别写出 、 、 的坐标;
求△ 的面积.
25. 如图,与中,与交于点E,且,.
(1)求证:;
(2)当,求的度数.
26. 如图,四边形ABCD中,AB=AC,∠D=90°,BE⊥AC于点F,交CD于点E,连接EA,EA平分∠DEF.
(1)求证:AF=AD;
(2)若BF=7, DE=3,求CE的长.
如图,等腰中,.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法).
①作的角平分线交于点D;
②在边的延长线上作一点E,使,连接.
在(1)所作的图形中,猜想线段与的数量关系,并证明.
28.如图1,在△ABC中,∠A=60°,BD,CE是△ABC的两条角平分线,且BD,CE交于点F.用等式表示BE,BC,CD这三条线段之间的数量关系,并证明你的结论.
图1 图2
小东通过观察、实验,提出猜想:BE+CD=BC.他发现先在BC上截取BM,使BM=BE,连接FM,如图2,再利用三角形全等的判定和性质证明CM=CD即可.
(1)下面是小东证明该猜想的部分思路,请补充完整:
①在BC上截取BM,使BM=BE,连接FM,则可以证明△BEF与___________全等,判定它们全等的依据是______________;
②由∠A=60°,BD,CE是△ABC的两条角平分线,可以得出∠EFB=______°;
(2)请直接利用①、②已得到的结论,完成证明猜想BE+CD=BC的过程.
第1页(共6页)
同课章节目录
