沪科版数学八年级上册 第12章 一次函数 基础复习(二)(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 第12章 一次函数 基础复习(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 545.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 10:03:10 | ||
图片预览

文档简介
第十二章 一次函数
知识点1 一次函数与二元一次方程
1. 一般地,一个二元一次方程可以转化为一次函数y= kx+b(k≠0)的形式,所以每个二元一次方程都对应一个一次函数,于是也对应一条直线.
2. 一般地,每个二元一次方程组都对应两个一次函数,于是也对应两条直线.二元一次方程组 的解为直线 和 的交点坐标;反过来,两直线 和 的交点坐标就是对应的二元一次方程组的解.
练习
1. 如图,在平面直角坐标系中,一次函数y= kx+b和y= mx+n相交于点(2,-1),则关于x,y的方程组 的解是 ( )
2. 二元一次方程组 的解为 则一次函数y=5-x与y=2x-1的交点坐标为 ( )
A.(2,3) B.(3,2) C.( -2,3) D.(2,-3)
3. 如图,下列方程组的解是直线l ,l 的交点坐标的是 ( )
4. 已知一次函数 与 的图象如图所示,则关于x与y的二元一次方程组 的解的个数为 ( )
A.0个 B.1个 C.2个 D.无数个
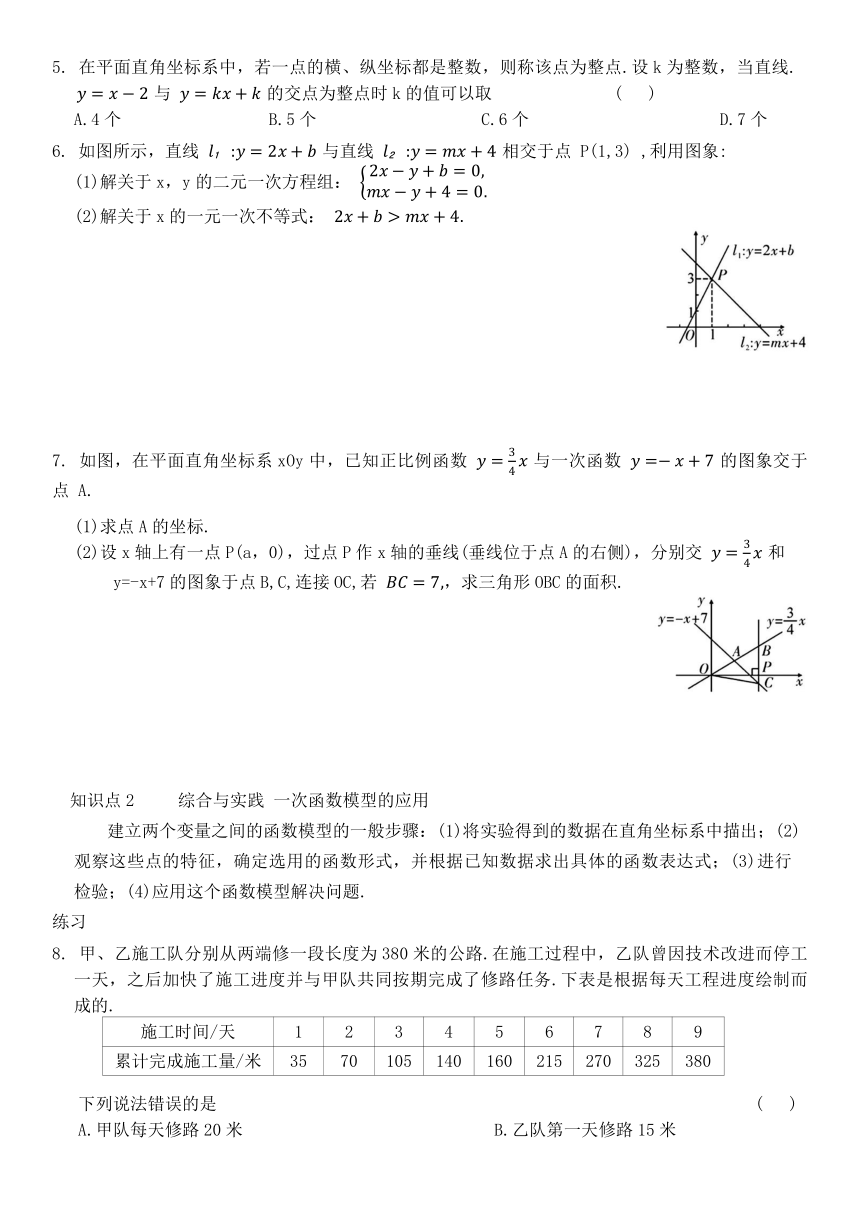
5. 在平面直角坐标系中,若一点的横、纵坐标都是整数,则称该点为整点.设k为整数,当直线. 与 的交点为整点时k的值可以取 ( )
A.4个 B.5个 C.6个 D.7个
6. 如图所示,直线 与直线 相交于点 P(1,3) ,利用图象:
(1)解关于x,y的二元一次方程组:
(2)解关于x的一元一次不等式:
7. 如图,在平面直角坐标系xOy中,已知正比例函数 与一次函数 的图象交于点 A.
(1)求点A的坐标.
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交 和
y=-x+7的图象于点B,C,连接OC,若 ,求三角形OBC的面积.
知识点2 综合与实践 一次函数模型的应用
建立两个变量之间的函数模型的一般步骤:(1)将实验得到的数据在直角坐标系中描出;(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;(3)进行检验;(4)应用这个函数模型解决问题.
练习
8. 甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
施工时间/天 1 2 3 4 5 6 7 8 9
累计完成施工量/米 35 70 105 140 160 215 270 325 380
下列说法错误的是 ( )
A.甲队每天修路20米 B.乙队第一天修路15米
C.乙队技术改进后每天修路35米 D.前七天甲、乙两队修路长度相等
9. 下列数据是弹簧挂重物后的伸长记录,当弹簧在弹性限度内挂30kg物体时,弹簧长 ( )
重物质量/ kg 0 1 2 3 4 30
弹簧长度/ cm 12 12.5 13 13.5 14
A.26 cm B.26.5cm C.27 cm D.27.5cm
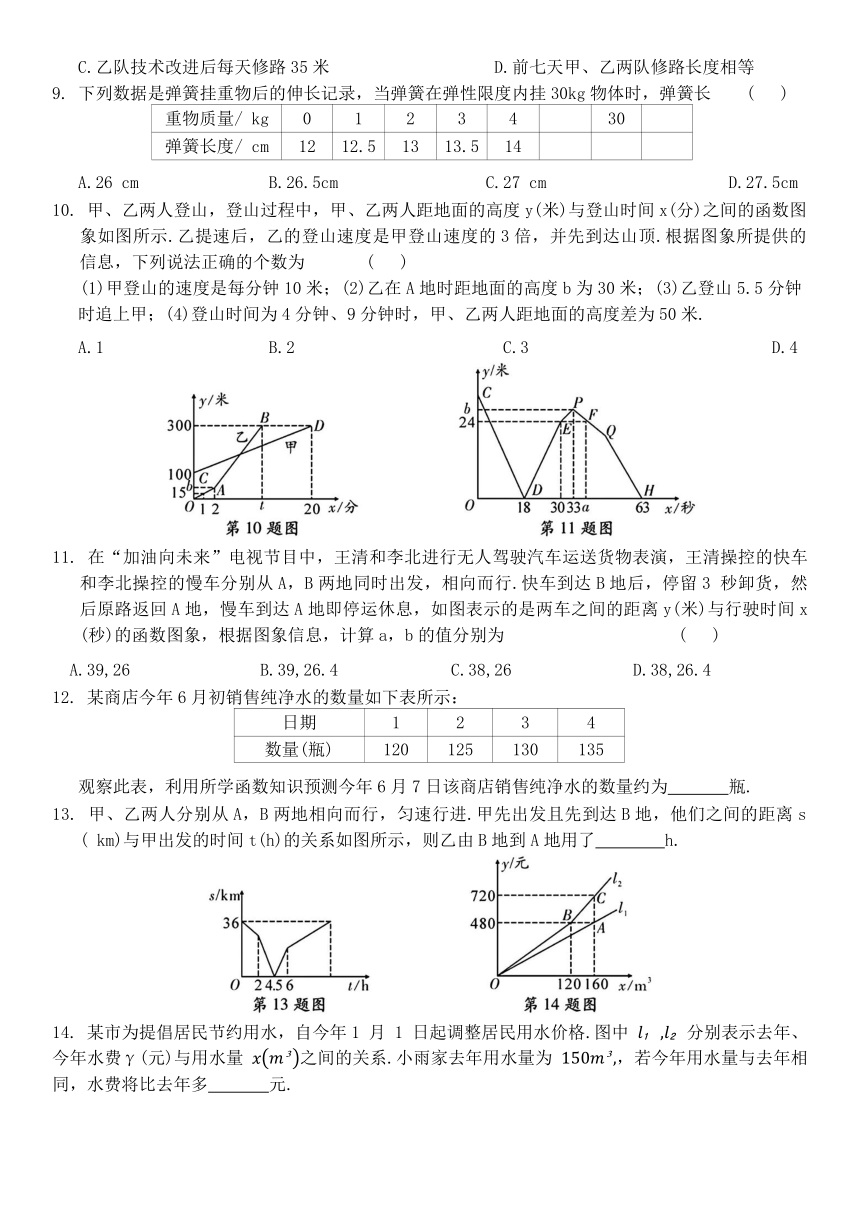
10. 甲、乙两人登山,登山过程中,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示.乙提速后,乙的登山速度是甲登山速度的3倍,并先到达山顶.根据图象所提供的信息,下列说法正确的个数为 ( )
(1)甲登山的速度是每分钟10米;(2)乙在A地时距地面的高度b为30米;(3)乙登山5.5分钟时追上甲;(4)登山时间为4分钟、9分钟时,甲、乙两人距地面的高度差为50米.
A.1 B.2 C.3 D.4
11. 在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行.快车到达B地后,停留3 秒卸货,然后原路返回A地,慢车到达A地即停运休息,如图表示的是两车之间的距离y(米)与行驶时间x(秒)的函数图象,根据图象信息,计算a,b的值分别为 ( )
A.39,26 B.39,26.4 C.38,26 D.38,26.4
12. 某商店今年6月初销售纯净水的数量如下表所示:
日期 1 2 3 4
数量(瓶) 120 125 130 135
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为 瓶.
13. 甲、乙两人分别从A,B两地相向而行,匀速行进.甲先出发且先到达B地,他们之间的距离s( km)与甲出发的时间t(h)的关系如图所示,则乙由B地到A地用了 h.
14. 某市为提倡居民节约用水,自今年1 月 1 日起调整居民用水价格.图中 分别表示去年、今年水费γ(元)与用水量 之间的关系.小雨家去年用水量为 ,若今年用水量与去年相同,水费将比去年多 元.
15. 小明练习100米短跑,训练时间与100 米短跑成绩记录如下:
时间(月) 1 2 3 4
成绩(秒) 15.6 15.4 15.2 15
(1)请你为小明的100米短跑成绩y(秒)与训练时间x(月)的关系建立函数模型.
(2)用所求出的函数表达式预测小明训练6个月的100米短跑成绩.
(3)能用所求出的函数表达式预测小明训练3年的100米短跑成绩吗 为什么
16. 某商业集团新进了40 台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:
空调机 电冰箱
甲连锁店 200 170
乙连锁店 160 150
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元).
(1)求y关于x的函数表达式,并求出x的取值范围.
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利a元销售,其他的销售利润不变,并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润,问该集团应该如何设计调配方案,使总利润达到最大
第十二章 一次函数
1. B 2. A 3. A 4. A 5. A
6.解:(1)直线 的解析式 对应的方程为 直线 的解析式 对应的方程为 因为直线 与直线 的交点坐标为P(1,3),所以关于x,y的二元一次方程组 的解为
(2)由题图可得,当x>1时,直线 在直线 的上方,即 即不等式: 的解集为
7.解:(1)由题联立方程组 解得 所以点A的坐标为(4,3).
(2)由题意,可得直线 BC的解析式为x=a.
解方程组 得 所以点 B的坐标为 解方程组
得 所以C的坐标为( 所以 因为 所以 解得 即 所以
8. D 9. C 10. C 11. B 12.150 13.10 14.210
15.解:(1)建立一次函数模型.设y= kx+b(k≠0),
依题意,得 解得
所以y=-0.2x+15.8.
经验证,均符合上式.
所以小明的100米短跑成绩y(秒)与训练时间x(月)的函数表达式为y= -0.2x+15.8.
(2)当x=6时,y=-0.2×6+15.8=14.6.
预测小明训练6个月的100米短跑成绩为14.6秒.
(3)不能,因为短跑的成绩在短时间内可能呈某种趋势,但在较长的时间内,受自身的发展极限的限制,不会永远如此快的提高.(理由合理即可)
16. 解:(1)由题意可知,调配给甲连锁店电冰箱(70-x)台,调配给乙连锁店空调机(40-x)台,电冰箱为60-(70-x)=(x-10)台,则y=200x+170(70-x)+160(40-x)+150(x-10),整理,得y=20x+16800.
由题意,得 解得 10≤x≤40.所以y= 20x+16 800(10≤x≤40).
(2)由题意,得y=(200-a)x+170×(70-x)+160×(40-x)+150×(x-10),
整理,得y=(20-a)x+16800.
因为200﹣a>170,所以a<30.
当00,函数y随x的增大而增大,故当x=40时,总利润最大,即调配给甲连锁店空调机40台,电冰箱30台,乙连锁店空调机0台,电冰箱30台;
当a= 20时,x的取值在10≤x≤40内的所有方案利润相同;
当20
知识点1 一次函数与二元一次方程
1. 一般地,一个二元一次方程可以转化为一次函数y= kx+b(k≠0)的形式,所以每个二元一次方程都对应一个一次函数,于是也对应一条直线.
2. 一般地,每个二元一次方程组都对应两个一次函数,于是也对应两条直线.二元一次方程组 的解为直线 和 的交点坐标;反过来,两直线 和 的交点坐标就是对应的二元一次方程组的解.
练习
1. 如图,在平面直角坐标系中,一次函数y= kx+b和y= mx+n相交于点(2,-1),则关于x,y的方程组 的解是 ( )
2. 二元一次方程组 的解为 则一次函数y=5-x与y=2x-1的交点坐标为 ( )
A.(2,3) B.(3,2) C.( -2,3) D.(2,-3)
3. 如图,下列方程组的解是直线l ,l 的交点坐标的是 ( )
4. 已知一次函数 与 的图象如图所示,则关于x与y的二元一次方程组 的解的个数为 ( )
A.0个 B.1个 C.2个 D.无数个
5. 在平面直角坐标系中,若一点的横、纵坐标都是整数,则称该点为整点.设k为整数,当直线. 与 的交点为整点时k的值可以取 ( )
A.4个 B.5个 C.6个 D.7个
6. 如图所示,直线 与直线 相交于点 P(1,3) ,利用图象:
(1)解关于x,y的二元一次方程组:
(2)解关于x的一元一次不等式:
7. 如图,在平面直角坐标系xOy中,已知正比例函数 与一次函数 的图象交于点 A.
(1)求点A的坐标.
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交 和
y=-x+7的图象于点B,C,连接OC,若 ,求三角形OBC的面积.
知识点2 综合与实践 一次函数模型的应用
建立两个变量之间的函数模型的一般步骤:(1)将实验得到的数据在直角坐标系中描出;(2)观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;(3)进行检验;(4)应用这个函数模型解决问题.
练习
8. 甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
施工时间/天 1 2 3 4 5 6 7 8 9
累计完成施工量/米 35 70 105 140 160 215 270 325 380
下列说法错误的是 ( )
A.甲队每天修路20米 B.乙队第一天修路15米
C.乙队技术改进后每天修路35米 D.前七天甲、乙两队修路长度相等
9. 下列数据是弹簧挂重物后的伸长记录,当弹簧在弹性限度内挂30kg物体时,弹簧长 ( )
重物质量/ kg 0 1 2 3 4 30
弹簧长度/ cm 12 12.5 13 13.5 14
A.26 cm B.26.5cm C.27 cm D.27.5cm
10. 甲、乙两人登山,登山过程中,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示.乙提速后,乙的登山速度是甲登山速度的3倍,并先到达山顶.根据图象所提供的信息,下列说法正确的个数为 ( )
(1)甲登山的速度是每分钟10米;(2)乙在A地时距地面的高度b为30米;(3)乙登山5.5分钟时追上甲;(4)登山时间为4分钟、9分钟时,甲、乙两人距地面的高度差为50米.
A.1 B.2 C.3 D.4
11. 在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行.快车到达B地后,停留3 秒卸货,然后原路返回A地,慢车到达A地即停运休息,如图表示的是两车之间的距离y(米)与行驶时间x(秒)的函数图象,根据图象信息,计算a,b的值分别为 ( )
A.39,26 B.39,26.4 C.38,26 D.38,26.4
12. 某商店今年6月初销售纯净水的数量如下表所示:
日期 1 2 3 4
数量(瓶) 120 125 130 135
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为 瓶.
13. 甲、乙两人分别从A,B两地相向而行,匀速行进.甲先出发且先到达B地,他们之间的距离s( km)与甲出发的时间t(h)的关系如图所示,则乙由B地到A地用了 h.
14. 某市为提倡居民节约用水,自今年1 月 1 日起调整居民用水价格.图中 分别表示去年、今年水费γ(元)与用水量 之间的关系.小雨家去年用水量为 ,若今年用水量与去年相同,水费将比去年多 元.
15. 小明练习100米短跑,训练时间与100 米短跑成绩记录如下:
时间(月) 1 2 3 4
成绩(秒) 15.6 15.4 15.2 15
(1)请你为小明的100米短跑成绩y(秒)与训练时间x(月)的关系建立函数模型.
(2)用所求出的函数表达式预测小明训练6个月的100米短跑成绩.
(3)能用所求出的函数表达式预测小明训练3年的100米短跑成绩吗 为什么
16. 某商业集团新进了40 台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:
空调机 电冰箱
甲连锁店 200 170
乙连锁店 160 150
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元).
(1)求y关于x的函数表达式,并求出x的取值范围.
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利a元销售,其他的销售利润不变,并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润,问该集团应该如何设计调配方案,使总利润达到最大
第十二章 一次函数
1. B 2. A 3. A 4. A 5. A
6.解:(1)直线 的解析式 对应的方程为 直线 的解析式 对应的方程为 因为直线 与直线 的交点坐标为P(1,3),所以关于x,y的二元一次方程组 的解为
(2)由题图可得,当x>1时,直线 在直线 的上方,即 即不等式: 的解集为
7.解:(1)由题联立方程组 解得 所以点A的坐标为(4,3).
(2)由题意,可得直线 BC的解析式为x=a.
解方程组 得 所以点 B的坐标为 解方程组
得 所以C的坐标为( 所以 因为 所以 解得 即 所以
8. D 9. C 10. C 11. B 12.150 13.10 14.210
15.解:(1)建立一次函数模型.设y= kx+b(k≠0),
依题意,得 解得
所以y=-0.2x+15.8.
经验证,均符合上式.
所以小明的100米短跑成绩y(秒)与训练时间x(月)的函数表达式为y= -0.2x+15.8.
(2)当x=6时,y=-0.2×6+15.8=14.6.
预测小明训练6个月的100米短跑成绩为14.6秒.
(3)不能,因为短跑的成绩在短时间内可能呈某种趋势,但在较长的时间内,受自身的发展极限的限制,不会永远如此快的提高.(理由合理即可)
16. 解:(1)由题意可知,调配给甲连锁店电冰箱(70-x)台,调配给乙连锁店空调机(40-x)台,电冰箱为60-(70-x)=(x-10)台,则y=200x+170(70-x)+160(40-x)+150(x-10),整理,得y=20x+16800.
由题意,得 解得 10≤x≤40.所以y= 20x+16 800(10≤x≤40).
(2)由题意,得y=(200-a)x+170×(70-x)+160×(40-x)+150×(x-10),
整理,得y=(20-a)x+16800.
因为200﹣a>170,所以a<30.
当0
当a= 20时,x的取值在10≤x≤40内的所有方案利润相同;
当20
