沪科版数学八年级上册 第12 章 一次函数 综合测试卷(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 第12 章 一次函数 综合测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 910.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 10:05:27 | ||
图片预览


文档简介
第 12 章综合测试卷
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 若正比例函数y=-2x的图象经过点O(a-1,4),则a的值为 ( )
A. -1 B.0 C.1 D.2
2. 一次函数y=2x-3的图象经过的象限是 ( )
A.一、二、三 B.二、三、四 C.一、三、四 D.一、二、四
3. 直线y=3x+1向下平移2个单位,所得直线的表达式是 ( )
A. y=3x+3 B. y=3x-2 C. y=3x+2 D. y=3x-1
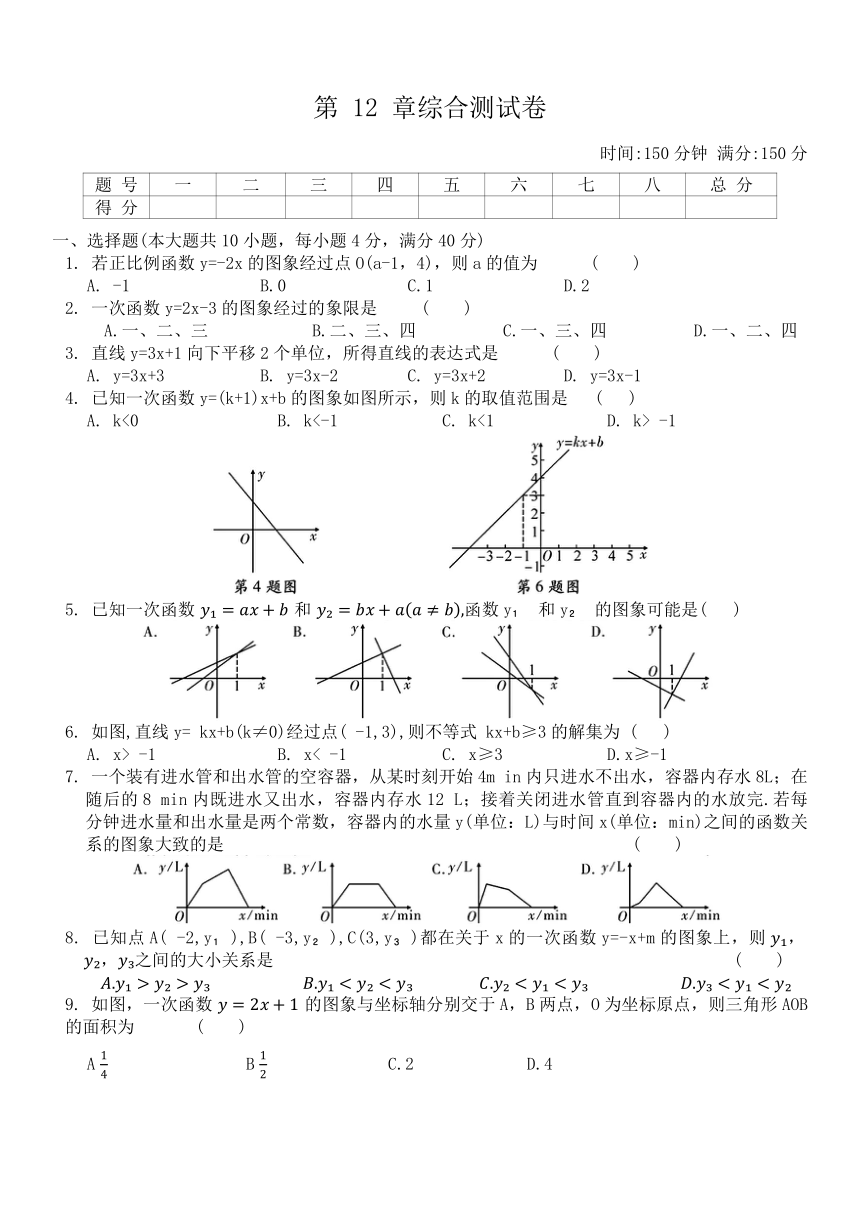
4. 已知一次函数y=(k+1)x+b的图象如图所示,则k的取值范围是 ( )
A. k<0 B. k<-1 C. k<1 D. k> -1
5. 已知一次函数 和 函数y 和y 的图象可能是( )
6. 如图,直线y= kx+b(k≠0)经过点( -1,3),则不等式 kx+b≥3的解集为 ( )
A. x> -1 B. x< -1 C. x≥3 D.x≥-1
7. 一个装有进水管和出水管的空容器,从某时刻开始4m in内只进水不出水,容器内存水8L;在随后的8 min内既进水又出水,容器内存水12 L;接着关闭进水管直到容器内的水放完.若每分钟进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的函数关系的图象大致的是 ( )
8. 已知点A( -2,y ),B( -3,y ),C(3,y )都在关于x的一次函数y=-x+m的图象上,则,,之间的大小关系是 ( )
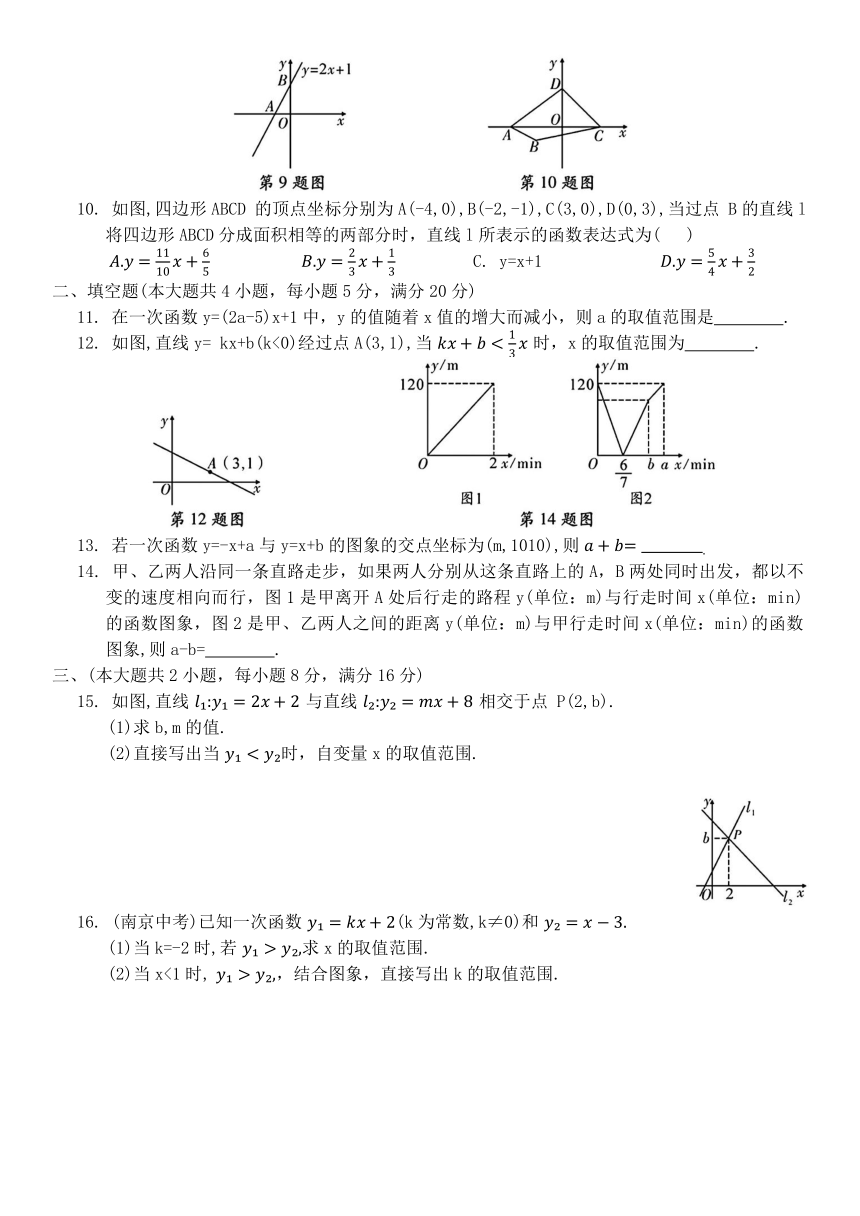
9. 如图,一次函数 的图象与坐标轴分别交于A,B两点,O为坐标原点,则三角形AOB的面积为 ( )
A B C.2 D.4
10. 如图,四边形ABCD 的顶点坐标分别为A(-4,0),B(-2,-1),C(3,0),D(0,3),当过点 B的直线l将四边形ABCD分成面积相等的两部分时,直线l所表示的函数表达式为( )
C. y=x+1
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 在一次函数y=(2a-5)x+1中,y的值随着x值的增大而减小,则a的取值范围是 .
12. 如图,直线y= kx+b(k<0)经过点A(3,1),当 时,x的取值范围为 .
13. 若一次函数y=-x+a与y=x+b的图象的交点坐标为(m,1010),则
14. 甲、乙两人沿同一条直路走步,如果两人分别从这条直路上的A,B两处同时出发,都以不变的速度相向而行,图1是甲离开A处后行走的路程y(单位:m)与行走时间x(单位:min)的函数图象,图2是甲、乙两人之间的距离y(单位:m)与甲行走时间x(单位:min)的函数图象,则a-b= .
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,直线 与直线 相交于点 P(2,b).
(1)求b,m的值.
(2)直接写出当 时,自变量x的取值范围.
16. (南京中考)已知一次函数 (k为常数,k≠0)和
(1)当k=-2时,若 求x的取值范围.
(2)当x<1时, ,结合图象,直接写出k的取值范围.
四、(本大题共2小题,每小题8分,满分16分)
17. 在平面直角坐标系中,一次函数y= kx+b(k,b,且k≠0)的图象经过点(1,0)和(0,3).
(1)求此函数的表达式.
(2)已知点P(m,n)在该函数的图象上,且m+n=4.
①求点 P 的坐标.
②若函数y= ax(a是常数,且a≠0)的图象与函数y= kx+b的图象相交于点P,写出不等式 ax< kx+b的解集.
18. 如图,直线y= kx+1(k≠0)与两坐标轴分别交于点A,B,直线y= -2x+4与y轴交于点C,与直线y= kx+1交于点D,三角形ACD的面积
(1)求k的值.
(2)直接写出不等式 kx+1<-2x+4的解集.
(3)已知点P在x轴上,如果三角形DBP的面积为4,求点P的坐标.
五、(本大题共2 小题,每小题10分,满分20分)
19. 新型冠状肺炎的爆发及蔓延,牵动了全国人民的心,也增强了大家的防护意识,因此,日常生活中开展科学、规范的防护工作显得十分重要.某社区为防控疫情传播,保障社区人员的生命安全,计划购买大量消毒液用于日常消毒.经了解,甲、乙两家公司推出的购买优惠方案如下:甲公司规定:每瓶消毒液一律按标价的八五折出售;乙公司规定:每瓶消毒液按标价出售,若购买数量超过20瓶则超出的部分打七折.
已知每瓶消毒液的标价为8元,若该社区计划购买消毒液共x瓶,购买甲公司消毒液所需费用为y 元,购买乙公司消毒液所需费用为y 元.
(1)分别求y 、y 与x之间的函数表达式.
(2)若该社区计划购买消毒液共60瓶,则选择哪一家公司比较合算
20. 关于函数 和函数 有如下信息:
①当x>2时,y根据信息解答下列问题:
(1)求函数y 的表达式.
(2)在平面直角坐标系xOy中,画出y ,y 的图象.
六、(本题满分12分)
21. 小明放学后从学校回家,出发5分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发10分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程y(米)与小强所用时间x(分钟)之间的函数图象如图所示.
(1)求函数图象中a的值.
(2)求小强的速度.
(3)求线段AB的函数表达式,并写出自变量的取值范围.
七、(本题满分12分)
22. 定义:函数 (其中 )为关于x的两个一次函数
与 的生成函数.请你解答下列问题:
(1)给定两个一次函数:
①求它们的生成函数在x=1时的函数值.
②判断这两个函数图象的交点是否在它们的生成函数的图象上,请说明理由.
(2)设两个一次函数 与 的图象的交点为P,判断点 P是否在它们的生成函数的图象上,并说明理由.
八、(本题满分14分)
23. (黑龙江中考)为庆祝中华人民共和国七十周年华诞,某广场舞团队准备购买甲、乙两种道具参加演出,已知购买2件甲种道具,1件乙种道具共需35元;购买1件甲种道具,3种乙种道具共需花费30元.
(1)求购买一件甲种道具,一件乙种道具各需多少元
(2)若该团体计划购买这两种道具共120件,投入资金不少于956元又不多于1 000元,设购买甲种道具x件,求有多少种购买方案
(3)设投入资金为W元,在(2)的条件下,哪种购买方案需要投入的资金最少 最少资金是多少元
第12 章综合测试卷
A 2. C 3. D 4. B 5. A 6. D 7. A 8. D 9. A 10. D 12. x>3
13.2020
15.解:(1)因为直线 与直线 相交于点 P(2,b),所以P(2,b)在 上,即b=2×2+2=6,所以P(2,6).
因为P(2,6)在 上,
所以2m+8=6,解得m=-1.所以b=6,m=-1.
(2)由图可知,当 时,自变量x的取值范围是x<2.
16.解:(1)当k=-2时,
根据题意,得-2x+2>x-3,解得
(2)当x=1时, ,把(1,-2)代入 得k+2=-2,解得k=-4,由图象可知,当-4≤k<0时, 当0所以k的取值范围为-4≤k≤1且k≠0.
17. 解:(1)将(1,0)和(0,3)代入y= kx+b,可得方程组解得所以此函数表达式为y=-3x+3.(2)①将P(m,n)带入y=-3x+3,得n=-3m+3.
又因为m+n=4,解得
所以点 P 坐标为
②由图可知,不等式( 的解集为
18. 解:(1)当x=0时,y= kx+1=1,则A(0,1),
当x=0时,y=-2x+4=4,则C(0,4),
设D点的坐标为(t,-2t+4),
因为三角形ACD的面积为
所以 解得t=1,
所以D(1,2),把D(1,2)代入y= kx+1得k+1=2,所以k=1.
(2)由图可知,不等式 kx+1<-2x+4的解集为x<1.
(3)当y=0时,x+1=0,解得x=-1,则B(-1,0),设P(m,0),因为三角形DBP 的面积为4,所以 解得m=-5或3,所以点 P 坐标为( -5,0)或(3,0).
19. 解:(1) =0.85×8x=6.8x;y =
化简,得
(2)当x=60时, (元),
y =5.6x+48=5.6×60+48=384(元),
因为384<408,所以该社区选择乙公司比较合算.
20. 解:(1)当x=2时, 由已知,得y ,y 的交点坐标为(2,3),y 与x轴的交点坐标为( -4,0),将(2,3)( -4,0)坐标代入y 的表达式,得
解得 所以
(2)y ,y 的图象如图所示.
21.解:
(2)小明的速度为:300÷5=60(米/分),
小强的速度为:[900-60×(12-10)]÷12=65(米/分).
(3)由题意,得B(12,780),
设AB所在直线的表达式为y= kx+b(k≠0),
把A(10,900),B(12,780)代入得
解得
所以线段AB 所在直线的函数表达式为γ=-60x+1 500(10≤x≤12).
22. 解:(1)①y=-2x+1和y=x-2的生成函数为y=m(-2x+1)+n(x-2),因为m+n=1,所以当x=1时,y=-m-n=-1.
②因为方程组 的解为
所以这两个函数图象的交点坐标为(1,-1).
因为当x=1时,y=-m-n=-1,
所以这两个函数图象的交点在在它们的生成函数的图象上.
(2)设点 P(x ,y )为两图象的交点,
则
生成函数为
当x=x 时,
所以点 P在它们的生成函数的图象上.
23. 解:(1)设购买一个甲种道具a元,一个乙种道具b元,由题意得 解得
答:购买一个甲种道具15元,一个乙种道具5元.
(2)根据题意,得955≤15x+5×(120-x)≤1000,解得35.5≤x≤40,因为x是整数,所以x=36,37,38,39,40,
所以有5种购买方案.
(3)w=15x+5×(120-x)=10x+600,
因为10>0,所以w随x的增大而增大,
所以当x=36时,w最小 =10×36+600=960(元),
所以120-36=84(件).
答:购买甲种道具36个,乙种道具84个时需要的资金最少,最少资金是960元.
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 若正比例函数y=-2x的图象经过点O(a-1,4),则a的值为 ( )
A. -1 B.0 C.1 D.2
2. 一次函数y=2x-3的图象经过的象限是 ( )
A.一、二、三 B.二、三、四 C.一、三、四 D.一、二、四
3. 直线y=3x+1向下平移2个单位,所得直线的表达式是 ( )
A. y=3x+3 B. y=3x-2 C. y=3x+2 D. y=3x-1
4. 已知一次函数y=(k+1)x+b的图象如图所示,则k的取值范围是 ( )
A. k<0 B. k<-1 C. k<1 D. k> -1
5. 已知一次函数 和 函数y 和y 的图象可能是( )
6. 如图,直线y= kx+b(k≠0)经过点( -1,3),则不等式 kx+b≥3的解集为 ( )
A. x> -1 B. x< -1 C. x≥3 D.x≥-1
7. 一个装有进水管和出水管的空容器,从某时刻开始4m in内只进水不出水,容器内存水8L;在随后的8 min内既进水又出水,容器内存水12 L;接着关闭进水管直到容器内的水放完.若每分钟进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的函数关系的图象大致的是 ( )
8. 已知点A( -2,y ),B( -3,y ),C(3,y )都在关于x的一次函数y=-x+m的图象上,则,,之间的大小关系是 ( )
9. 如图,一次函数 的图象与坐标轴分别交于A,B两点,O为坐标原点,则三角形AOB的面积为 ( )
A B C.2 D.4
10. 如图,四边形ABCD 的顶点坐标分别为A(-4,0),B(-2,-1),C(3,0),D(0,3),当过点 B的直线l将四边形ABCD分成面积相等的两部分时,直线l所表示的函数表达式为( )
C. y=x+1
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 在一次函数y=(2a-5)x+1中,y的值随着x值的增大而减小,则a的取值范围是 .
12. 如图,直线y= kx+b(k<0)经过点A(3,1),当 时,x的取值范围为 .
13. 若一次函数y=-x+a与y=x+b的图象的交点坐标为(m,1010),则
14. 甲、乙两人沿同一条直路走步,如果两人分别从这条直路上的A,B两处同时出发,都以不变的速度相向而行,图1是甲离开A处后行走的路程y(单位:m)与行走时间x(单位:min)的函数图象,图2是甲、乙两人之间的距离y(单位:m)与甲行走时间x(单位:min)的函数图象,则a-b= .
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,直线 与直线 相交于点 P(2,b).
(1)求b,m的值.
(2)直接写出当 时,自变量x的取值范围.
16. (南京中考)已知一次函数 (k为常数,k≠0)和
(1)当k=-2时,若 求x的取值范围.
(2)当x<1时, ,结合图象,直接写出k的取值范围.
四、(本大题共2小题,每小题8分,满分16分)
17. 在平面直角坐标系中,一次函数y= kx+b(k,b,且k≠0)的图象经过点(1,0)和(0,3).
(1)求此函数的表达式.
(2)已知点P(m,n)在该函数的图象上,且m+n=4.
①求点 P 的坐标.
②若函数y= ax(a是常数,且a≠0)的图象与函数y= kx+b的图象相交于点P,写出不等式 ax< kx+b的解集.
18. 如图,直线y= kx+1(k≠0)与两坐标轴分别交于点A,B,直线y= -2x+4与y轴交于点C,与直线y= kx+1交于点D,三角形ACD的面积
(1)求k的值.
(2)直接写出不等式 kx+1<-2x+4的解集.
(3)已知点P在x轴上,如果三角形DBP的面积为4,求点P的坐标.
五、(本大题共2 小题,每小题10分,满分20分)
19. 新型冠状肺炎的爆发及蔓延,牵动了全国人民的心,也增强了大家的防护意识,因此,日常生活中开展科学、规范的防护工作显得十分重要.某社区为防控疫情传播,保障社区人员的生命安全,计划购买大量消毒液用于日常消毒.经了解,甲、乙两家公司推出的购买优惠方案如下:甲公司规定:每瓶消毒液一律按标价的八五折出售;乙公司规定:每瓶消毒液按标价出售,若购买数量超过20瓶则超出的部分打七折.
已知每瓶消毒液的标价为8元,若该社区计划购买消毒液共x瓶,购买甲公司消毒液所需费用为y 元,购买乙公司消毒液所需费用为y 元.
(1)分别求y 、y 与x之间的函数表达式.
(2)若该社区计划购买消毒液共60瓶,则选择哪一家公司比较合算
20. 关于函数 和函数 有如下信息:
①当x>2时,y
(1)求函数y 的表达式.
(2)在平面直角坐标系xOy中,画出y ,y 的图象.
六、(本题满分12分)
21. 小明放学后从学校回家,出发5分钟时,同桌小强发现小明的数学作业卷忘记拿了,立即拿着数学作业卷按照同样的路线去追赶小明,小强出发10分钟时,小明才想起没拿数学作业卷,马上以原速原路返回,在途中与小强相遇.两人离学校的路程y(米)与小强所用时间x(分钟)之间的函数图象如图所示.
(1)求函数图象中a的值.
(2)求小强的速度.
(3)求线段AB的函数表达式,并写出自变量的取值范围.
七、(本题满分12分)
22. 定义:函数 (其中 )为关于x的两个一次函数
与 的生成函数.请你解答下列问题:
(1)给定两个一次函数:
①求它们的生成函数在x=1时的函数值.
②判断这两个函数图象的交点是否在它们的生成函数的图象上,请说明理由.
(2)设两个一次函数 与 的图象的交点为P,判断点 P是否在它们的生成函数的图象上,并说明理由.
八、(本题满分14分)
23. (黑龙江中考)为庆祝中华人民共和国七十周年华诞,某广场舞团队准备购买甲、乙两种道具参加演出,已知购买2件甲种道具,1件乙种道具共需35元;购买1件甲种道具,3种乙种道具共需花费30元.
(1)求购买一件甲种道具,一件乙种道具各需多少元
(2)若该团体计划购买这两种道具共120件,投入资金不少于956元又不多于1 000元,设购买甲种道具x件,求有多少种购买方案
(3)设投入资金为W元,在(2)的条件下,哪种购买方案需要投入的资金最少 最少资金是多少元
第12 章综合测试卷
A 2. C 3. D 4. B 5. A 6. D 7. A 8. D 9. A 10. D 12. x>3
13.2020
15.解:(1)因为直线 与直线 相交于点 P(2,b),所以P(2,b)在 上,即b=2×2+2=6,所以P(2,6).
因为P(2,6)在 上,
所以2m+8=6,解得m=-1.所以b=6,m=-1.
(2)由图可知,当 时,自变量x的取值范围是x<2.
16.解:(1)当k=-2时,
根据题意,得-2x+2>x-3,解得
(2)当x=1时, ,把(1,-2)代入 得k+2=-2,解得k=-4,由图象可知,当-4≤k<0时, 当0
17. 解:(1)将(1,0)和(0,3)代入y= kx+b,可得方程组解得所以此函数表达式为y=-3x+3.(2)①将P(m,n)带入y=-3x+3,得n=-3m+3.
又因为m+n=4,解得
所以点 P 坐标为
②由图可知,不等式( 的解集为
18. 解:(1)当x=0时,y= kx+1=1,则A(0,1),
当x=0时,y=-2x+4=4,则C(0,4),
设D点的坐标为(t,-2t+4),
因为三角形ACD的面积为
所以 解得t=1,
所以D(1,2),把D(1,2)代入y= kx+1得k+1=2,所以k=1.
(2)由图可知,不等式 kx+1<-2x+4的解集为x<1.
(3)当y=0时,x+1=0,解得x=-1,则B(-1,0),设P(m,0),因为三角形DBP 的面积为4,所以 解得m=-5或3,所以点 P 坐标为( -5,0)或(3,0).
19. 解:(1) =0.85×8x=6.8x;y =
化简,得
(2)当x=60时, (元),
y =5.6x+48=5.6×60+48=384(元),
因为384<408,所以该社区选择乙公司比较合算.
20. 解:(1)当x=2时, 由已知,得y ,y 的交点坐标为(2,3),y 与x轴的交点坐标为( -4,0),将(2,3)( -4,0)坐标代入y 的表达式,得
解得 所以
(2)y ,y 的图象如图所示.
21.解:
(2)小明的速度为:300÷5=60(米/分),
小强的速度为:[900-60×(12-10)]÷12=65(米/分).
(3)由题意,得B(12,780),
设AB所在直线的表达式为y= kx+b(k≠0),
把A(10,900),B(12,780)代入得
解得
所以线段AB 所在直线的函数表达式为γ=-60x+1 500(10≤x≤12).
22. 解:(1)①y=-2x+1和y=x-2的生成函数为y=m(-2x+1)+n(x-2),因为m+n=1,所以当x=1时,y=-m-n=-1.
②因为方程组 的解为
所以这两个函数图象的交点坐标为(1,-1).
因为当x=1时,y=-m-n=-1,
所以这两个函数图象的交点在在它们的生成函数的图象上.
(2)设点 P(x ,y )为两图象的交点,
则
生成函数为
当x=x 时,
所以点 P在它们的生成函数的图象上.
23. 解:(1)设购买一个甲种道具a元,一个乙种道具b元,由题意得 解得
答:购买一个甲种道具15元,一个乙种道具5元.
(2)根据题意,得955≤15x+5×(120-x)≤1000,解得35.5≤x≤40,因为x是整数,所以x=36,37,38,39,40,
所以有5种购买方案.
(3)w=15x+5×(120-x)=10x+600,
因为10>0,所以w随x的增大而增大,
所以当x=36时,w最小 =10×36+600=960(元),
所以120-36=84(件).
答:购买甲种道具36个,乙种道具84个时需要的资金最少,最少资金是960元.
