沪科版数学八年级上册 期中综合测试卷(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 期中综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 952.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 10:08:43 | ||
图片预览


文档简介
期中综合测试卷
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 已知点P(m+2,2m﹣4)在y轴上,则点P的坐标是 ( )
A.(8,0) B.(0,-8) C.(-8,0) D.(0,8)
2. 在下列长度的三条线段中,不能组成三角形的是 ( )
A. 2cm , 3cm,4cm B. 3cm,6cm,6 cm
C. 2cm, 2cm ,6cm D. 5cm ,6cm,7cm
3. 下列命题中:①若 mn=0,则点A(m,n)在原点处;②点 )一定在第四象限;③已知点
A(m,n)与点B(﹣m,n),m,n均不为0,则直线AB平行x轴;④已知点A(2,﹣3),AB∥y轴,且
AB=5,则B点的坐标为(2,4),是真命题的有 ( )
A.1个 B.2个 C.3个 D.4个
4. 若点P在一次函数y=-x+4的图象上,则点P一定不在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5. 如图,已知函数 和 图象交于点P( -4,-2),当 时,根据图象可得x的取值范围是 ( )
A. x< -4 B. x> -4 C. -46. 如图,已知在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=20°,则∠AEB的度数为( )
A.100° B.110° C.120° D.130°
7. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法错误的是 ( )
A.体育场离林茂家2.5k m
B.体育场离文具店 1 km
C.林茂从体育场出发到文具店的平均速度是50 m/ min
D.林茂从文具店回家的平均速度是60 m/ min
8. 平面直角坐标系中,点A(-3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为 ( )
A.6,(-3,4) B.2,(3,2) C.2,(3,0) D.3,(3,2)
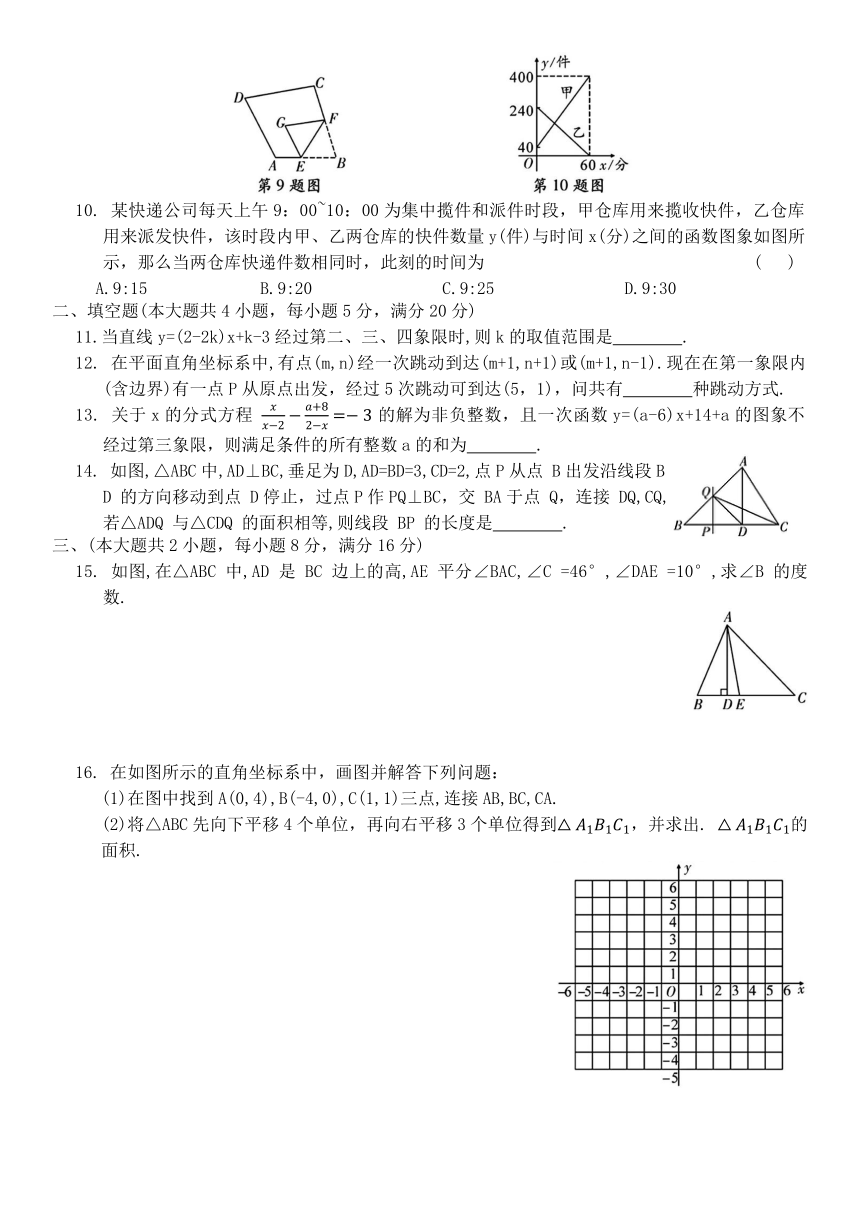
9. 如图,四边形ABCD中,点E,F分别在AB,BC上,将△BEF 沿EF翻折得△GEF,若EG∥AD,
FG∥DC,则以下结论一定成立的是 ( )
A.∠D=∠B B.∠D=180°-∠B
C.∠D=∠C D.∠D=180°-∠C
10. 某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为 ( )
A.9:15 B.9:20 C.9:25 D.9:30
二、填空题(本大题共4小题,每小题5分,满分20分)
11.当直线y=(2-2k)x+k-3经过第二、三、四象限时,则k的取值范围是 .
12. 在平面直角坐标系中,有点(m,n)经一次跳动到达(m+1,n+1)或(m+1,n-1).现在在第一象限内(含边界)有一点P从原点出发,经过5次跳动可到达(5,1),问共有 种跳动方式.
13. 关于x的分式方程 的解为非负整数,且一次函数y=(a-6)x+14+a的图象不经过第三象限,则满足条件的所有整数a的和为 .
14. 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点 B出发沿线段BD 的方向移动到点 D停止,过点P作PQ⊥BC,交 BA于点 Q,连接 DQ,CQ,若△ADQ 与△CDQ 的面积相等,则线段 BP 的长度是 .
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,在△ABC 中,AD 是 BC 边上的高,AE 平分∠BAC,∠C =46°,∠DAE =10°,求∠B 的度数.
16. 在如图所示的直角坐标系中,画图并解答下列问题:
(1)在图中找到A(0,4),B(-4,0),C(1,1)三点,连接AB,BC,CA.
(2)将△ABC先向下平移4个单位,再向右平移3个单位得到,并求出. 的面积.
四、(本大题共2小题,每小题8分,满分16分)
17. 如图,经过点 B(1,0)的直线l1 与直线 相交于点 P( -1,n).
(1)求n的值.
(2)求△PAB的面积.
18. 如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且 若记 ∠ACB=y(y≥x),,求∠CFE的大小.(用含x,y的代数式表示)
五、(本大题共2 小题,每小题10分,满分20分)
19. 如图,已知直线 直线 与l 相交于点P,l1,l 分别与y轴相交于点A,B.
(1)求点 P的坐标.
(2)若 求x|的取值范围.
(3)点D(m,0)为x轴上的一个动点,过点D作x轴的垂线分别交l1和l 于点E,F,当EF=3时,求m的值.
20. 如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足 过点C作 轴于点 B.
(1)求A,C 两点坐标.
(2)若过点B作BD∥AC交y轴于点D,且AE,DE分别平分. ,如图2,求 的度数.
六、(本题满分12分)
21. 在抗击新冠肺炎这场没有硝烟的战疫中,无人机成为全国各地广大农村乃至城区防疫消杀工作的“超级神器”,通过无人机隔空喊话宣传劝导,这使无人机成为宣传小能手.某市区也启用无人机进行防疫巡视及宣传工作.在操控无人机时,需根据现场状况调节无人机飞行高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行时间为x(分钟),对应的飞行高度为y(米),且y与x之间的函数图象如图所示.
(1)求线段BC所表示的y与x之间的函数表达式.
(2)求无人机在50米上空持续飞行的时间.
七、(本题满分12分)
22. 对于平面直角坐标系xOy中的点P(a,b),若点 P1 的坐标为( (其中k为常数,且k≠0),则称点P1为点P的“k属派生点”.例如,P(1,4)的“2属派生点”为
2×1+4),即P1(9,6).
(1)点( -2,3)的“3属派生点”P1的坐标为 .
(2)若点P的“5属派生点”P1的坐标为(3,-9),则点P坐标为 ;
(3)若x轴正半轴上一点P(a,0)的“k属派生点”为P1,且线段 的长度为线段OP长度的2倍,求k的值.
八、(本题满分14分)
23. 如图1,点A,B分别在射线OM,ON上运动(不与点O重合),AC,BC分别是∠BAO和∠ABO的角平分线,BC延长线交 OM于点 G.
(1)若∠MON=60°,则∠ACG= °.
(2)若∠MON=n°.请求出∠ACG的度数.(用含n的代数式表示)
(3)如图2,若∠MON=n°,过C作直线与AB交于点F.若CF∥OA时,求∠BGO-∠ACF 的度数.(用含n的代数式表示)
期中综合测试卷
B 2. C 3. A 4. C 5. B 6. B 7. C 8. D 9. A 10. B 11.113. -22
15.解:∵AD⊥BC,∴∠ADC=90°,∵∠C=46°,∴∠CAD=44°,
∵∠DAE=10°,∴∠CAE=34°,
∵AE平分∠BAC,∴∠BAC=2∠EAC=68°,
∴∠B=180°--∠BAC--∠C=66°.
16.解:(1)如图,△ABC即为所求.
(2)如图,即为所求.
17.解:(1)∵点. 在直线 上,
(2)∵直线 与x轴相交于点A.
解得
∴A点的坐标为
18.解: AD 平分
19.解:(1)根据题意,得 解得
∴点P的坐标为( -2,1).
(2)在直线 中,令y=0,解得x= -3,由图象,可知若 ,x的取值范围是-3(3)由题意,可知E(m,-2m-3),F(m,m+3),∵EF=3,∴ l-2m-3-m-3|=3,解得m=-3或m=-1.
20.解:(
∴a+2=0,b-2=0,
即a=-2,b=2,∴A(-2,0),C(2,2).
(2)∵ CB∥y轴,BD∥AC,
∴∠CAB=∠OBD,∠ODB=∠CBG,
∴∠CAB + ∠ODB = ∠OBD + ∠CBG =180°-
90°=90°,过点E作EF∥AC,如图,
∵BD∥AC,∴BD∥EF∥AC,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠AED的度数为45°.
21.解:(1)由题意,得60÷(12-9)=20(米/分),( (分),∴点C的坐标为(6,60).
设线段BC所表示的函数关系式为y= kx +b(k≠0),将B(5,40),C(6,60)代人y= kx+b,
得 解得
∴线段BC所表示的函数表达式为y=20x-60(5≤x≤6).
(2)设线段DE所表示的函数关系式为y= mx+n(m≠0),将D(9 ,60),E(12,0)代人y= mx+n,
得 解得
∴线段 DE 所表示的函数表达式为
当y=50时,有20x-60=50或-20x+240=50,
解得 或 (分钟).
答:无人机在50米上空持续飞行的时间为4分钟.
22.解:(1)由题意,得 ,即P1(7,-3);故答案为:(7,-3).
(2)由题意,得 解得故答案为:(-2,1).
(3)∵P(a,0)的“k属派生点”为P1(a, ka),
∴PP1的长度为| ka|,OP长度为a,
∵线段PP1 的长度为线段OP长度的2倍,
∴lkal=2a,∴k=±2,
23.解:(1)60°.
(2)在△AOB中,∵∠AOB=n°,
∵∠OBA,∠OAB的平分线交于点 C,
即
(3)∵AC,BC分别是∠BAO和∠ABO的角平分线,
∵CF∥AO,∴∠ACF=∠CAG,
∵∠BGO=∠BAG+∠ABG,
∴∠BGO--∠ACF=∠BAG+∠ABG-∠ACF=2∠BAC+∠ABG--∠BAC
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 已知点P(m+2,2m﹣4)在y轴上,则点P的坐标是 ( )
A.(8,0) B.(0,-8) C.(-8,0) D.(0,8)
2. 在下列长度的三条线段中,不能组成三角形的是 ( )
A. 2cm , 3cm,4cm B. 3cm,6cm,6 cm
C. 2cm, 2cm ,6cm D. 5cm ,6cm,7cm
3. 下列命题中:①若 mn=0,则点A(m,n)在原点处;②点 )一定在第四象限;③已知点
A(m,n)与点B(﹣m,n),m,n均不为0,则直线AB平行x轴;④已知点A(2,﹣3),AB∥y轴,且
AB=5,则B点的坐标为(2,4),是真命题的有 ( )
A.1个 B.2个 C.3个 D.4个
4. 若点P在一次函数y=-x+4的图象上,则点P一定不在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5. 如图,已知函数 和 图象交于点P( -4,-2),当 时,根据图象可得x的取值范围是 ( )
A. x< -4 B. x> -4 C. -4
A.100° B.110° C.120° D.130°
7. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法错误的是 ( )
A.体育场离林茂家2.5k m
B.体育场离文具店 1 km
C.林茂从体育场出发到文具店的平均速度是50 m/ min
D.林茂从文具店回家的平均速度是60 m/ min
8. 平面直角坐标系中,点A(-3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为 ( )
A.6,(-3,4) B.2,(3,2) C.2,(3,0) D.3,(3,2)
9. 如图,四边形ABCD中,点E,F分别在AB,BC上,将△BEF 沿EF翻折得△GEF,若EG∥AD,
FG∥DC,则以下结论一定成立的是 ( )
A.∠D=∠B B.∠D=180°-∠B
C.∠D=∠C D.∠D=180°-∠C
10. 某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为 ( )
A.9:15 B.9:20 C.9:25 D.9:30
二、填空题(本大题共4小题,每小题5分,满分20分)
11.当直线y=(2-2k)x+k-3经过第二、三、四象限时,则k的取值范围是 .
12. 在平面直角坐标系中,有点(m,n)经一次跳动到达(m+1,n+1)或(m+1,n-1).现在在第一象限内(含边界)有一点P从原点出发,经过5次跳动可到达(5,1),问共有 种跳动方式.
13. 关于x的分式方程 的解为非负整数,且一次函数y=(a-6)x+14+a的图象不经过第三象限,则满足条件的所有整数a的和为 .
14. 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点 B出发沿线段BD 的方向移动到点 D停止,过点P作PQ⊥BC,交 BA于点 Q,连接 DQ,CQ,若△ADQ 与△CDQ 的面积相等,则线段 BP 的长度是 .
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,在△ABC 中,AD 是 BC 边上的高,AE 平分∠BAC,∠C =46°,∠DAE =10°,求∠B 的度数.
16. 在如图所示的直角坐标系中,画图并解答下列问题:
(1)在图中找到A(0,4),B(-4,0),C(1,1)三点,连接AB,BC,CA.
(2)将△ABC先向下平移4个单位,再向右平移3个单位得到,并求出. 的面积.
四、(本大题共2小题,每小题8分,满分16分)
17. 如图,经过点 B(1,0)的直线l1 与直线 相交于点 P( -1,n).
(1)求n的值.
(2)求△PAB的面积.
18. 如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且 若记 ∠ACB=y(y≥x),,求∠CFE的大小.(用含x,y的代数式表示)
五、(本大题共2 小题,每小题10分,满分20分)
19. 如图,已知直线 直线 与l 相交于点P,l1,l 分别与y轴相交于点A,B.
(1)求点 P的坐标.
(2)若 求x|的取值范围.
(3)点D(m,0)为x轴上的一个动点,过点D作x轴的垂线分别交l1和l 于点E,F,当EF=3时,求m的值.
20. 如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足 过点C作 轴于点 B.
(1)求A,C 两点坐标.
(2)若过点B作BD∥AC交y轴于点D,且AE,DE分别平分. ,如图2,求 的度数.
六、(本题满分12分)
21. 在抗击新冠肺炎这场没有硝烟的战疫中,无人机成为全国各地广大农村乃至城区防疫消杀工作的“超级神器”,通过无人机隔空喊话宣传劝导,这使无人机成为宣传小能手.某市区也启用无人机进行防疫巡视及宣传工作.在操控无人机时,需根据现场状况调节无人机飞行高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行时间为x(分钟),对应的飞行高度为y(米),且y与x之间的函数图象如图所示.
(1)求线段BC所表示的y与x之间的函数表达式.
(2)求无人机在50米上空持续飞行的时间.
七、(本题满分12分)
22. 对于平面直角坐标系xOy中的点P(a,b),若点 P1 的坐标为( (其中k为常数,且k≠0),则称点P1为点P的“k属派生点”.例如,P(1,4)的“2属派生点”为
2×1+4),即P1(9,6).
(1)点( -2,3)的“3属派生点”P1的坐标为 .
(2)若点P的“5属派生点”P1的坐标为(3,-9),则点P坐标为 ;
(3)若x轴正半轴上一点P(a,0)的“k属派生点”为P1,且线段 的长度为线段OP长度的2倍,求k的值.
八、(本题满分14分)
23. 如图1,点A,B分别在射线OM,ON上运动(不与点O重合),AC,BC分别是∠BAO和∠ABO的角平分线,BC延长线交 OM于点 G.
(1)若∠MON=60°,则∠ACG= °.
(2)若∠MON=n°.请求出∠ACG的度数.(用含n的代数式表示)
(3)如图2,若∠MON=n°,过C作直线与AB交于点F.若CF∥OA时,求∠BGO-∠ACF 的度数.(用含n的代数式表示)
期中综合测试卷
B 2. C 3. A 4. C 5. B 6. B 7. C 8. D 9. A 10. B 11.1
15.解:∵AD⊥BC,∴∠ADC=90°,∵∠C=46°,∴∠CAD=44°,
∵∠DAE=10°,∴∠CAE=34°,
∵AE平分∠BAC,∴∠BAC=2∠EAC=68°,
∴∠B=180°--∠BAC--∠C=66°.
16.解:(1)如图,△ABC即为所求.
(2)如图,即为所求.
17.解:(1)∵点. 在直线 上,
(2)∵直线 与x轴相交于点A.
解得
∴A点的坐标为
18.解: AD 平分
19.解:(1)根据题意,得 解得
∴点P的坐标为( -2,1).
(2)在直线 中,令y=0,解得x= -3,由图象,可知若 ,x的取值范围是-3
20.解:(
∴a+2=0,b-2=0,
即a=-2,b=2,∴A(-2,0),C(2,2).
(2)∵ CB∥y轴,BD∥AC,
∴∠CAB=∠OBD,∠ODB=∠CBG,
∴∠CAB + ∠ODB = ∠OBD + ∠CBG =180°-
90°=90°,过点E作EF∥AC,如图,
∵BD∥AC,∴BD∥EF∥AC,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠AED的度数为45°.
21.解:(1)由题意,得60÷(12-9)=20(米/分),( (分),∴点C的坐标为(6,60).
设线段BC所表示的函数关系式为y= kx +b(k≠0),将B(5,40),C(6,60)代人y= kx+b,
得 解得
∴线段BC所表示的函数表达式为y=20x-60(5≤x≤6).
(2)设线段DE所表示的函数关系式为y= mx+n(m≠0),将D(9 ,60),E(12,0)代人y= mx+n,
得 解得
∴线段 DE 所表示的函数表达式为
当y=50时,有20x-60=50或-20x+240=50,
解得 或 (分钟).
答:无人机在50米上空持续飞行的时间为4分钟.
22.解:(1)由题意,得 ,即P1(7,-3);故答案为:(7,-3).
(2)由题意,得 解得故答案为:(-2,1).
(3)∵P(a,0)的“k属派生点”为P1(a, ka),
∴PP1的长度为| ka|,OP长度为a,
∵线段PP1 的长度为线段OP长度的2倍,
∴lkal=2a,∴k=±2,
23.解:(1)60°.
(2)在△AOB中,∵∠AOB=n°,
∵∠OBA,∠OAB的平分线交于点 C,
即
(3)∵AC,BC分别是∠BAO和∠ABO的角平分线,
∵CF∥AO,∴∠ACF=∠CAG,
∵∠BGO=∠BAG+∠ABG,
∴∠BGO--∠ACF=∠BAG+∠ABG-∠ACF=2∠BAC+∠ABG--∠BAC
同课章节目录
