第一章 勾股定理 分类提升训练(含答案) 2024--2025学年 北师大版 八年级数学上册
文档属性
| 名称 | 第一章 勾股定理 分类提升训练(含答案) 2024--2025学年 北师大版 八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 474.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 09:26:29 | ||
图片预览


文档简介
第一章 勾股定理 分类提升训练 2024--2025学年 北师大版 八年级数学上册
一、单选题
1.学了“勾股定理”后,甲、乙两位同学的观点如下:
甲:如果是直角三角形,那么一定成立;
乙:在中,如果,那么不是直角三角形.
对于两人的观点,下列说法正确的是( )
A.甲对,乙错 B.甲错,乙对 C.两人都错 D.两人都对
2.如图,在中,,分别以,为边向外作正方形,面积分别为,,若,,则的长为( )
A.4 B.2 C. D.3
3.为预防新冠疫情,民生大院入口的正上方处装有红外线激光测温仪(如图所示),测温仪离地面的距离米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为米的市民正对门缓慢走到离门米的地方时(即米),测温仪自动显示体温,则人头顶离测温仪的距离等于( )
A.米 B.米 C.米 D.米
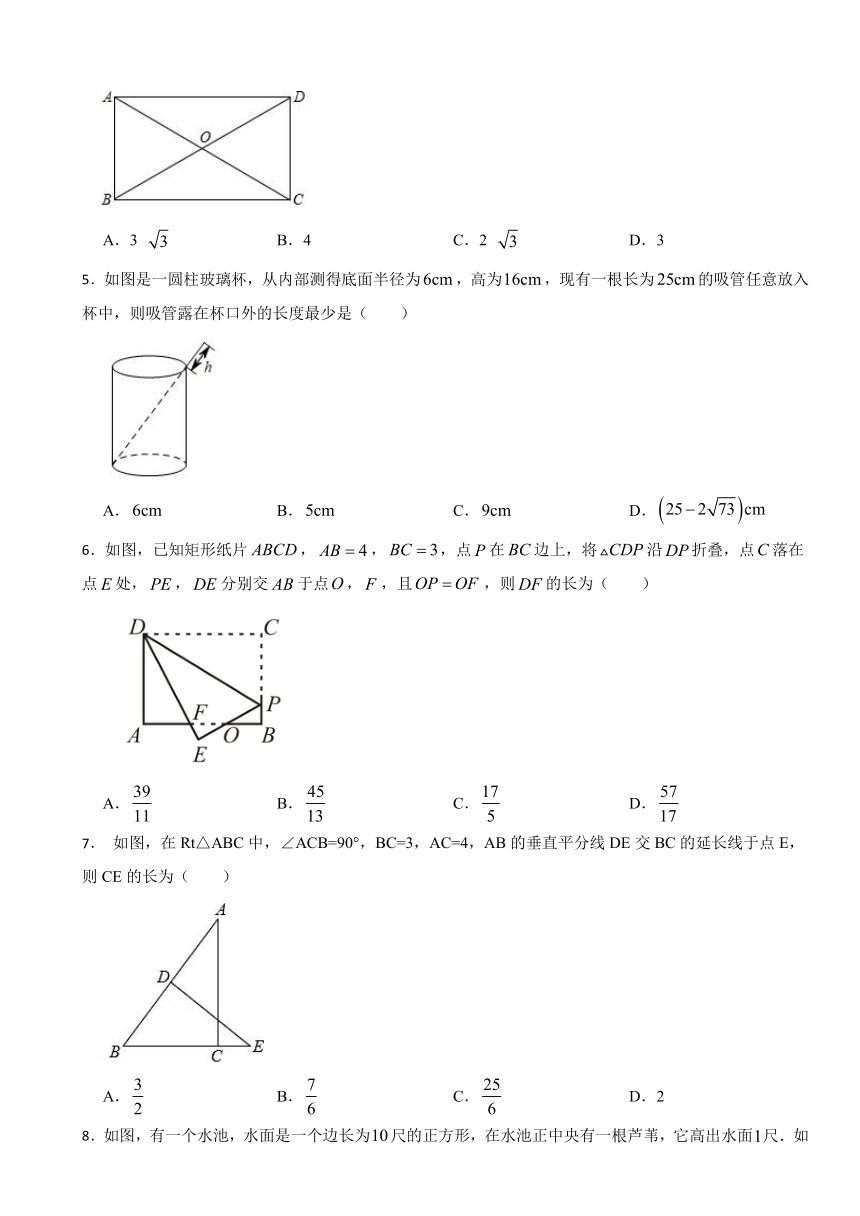
4.如图,矩形ABCD的对角线AC、BD相交于点O,∠ABO=60°,若矩形的对角线长为6.则线段AD的长是( )
A.3 B.4 C.2 D.3
5.如图是一圆柱玻璃杯,从内部测得底面半径为,高为,现有一根长为的吸管任意放入杯中,则吸管露在杯口外的长度最少是( )
A. B. C. D.
6.如图,已知矩形纸片,,,点在边上,将沿折叠,点落在点处,,分别交于点,,且,则的长为( )
A. B. C. D.
7. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
A. B. C. D.2
8.如图,有一个水池,水面是一个边长为尺的正方形,在水池正中央有一根芦苇,它高出水面尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面、求这根芦苇的长度是多少尺?设芦苇的长度是尺,根据题意,可列方程为( )
A. B.
C. D.
9.如图,过矩形对角线的交点,作对角线的垂线,交于点,交于点,若,,则的长等于( )
A. B. C. D.
10.在Rt中,.以为圆心,AM的长为半径作弧,分别交AC,AB于点M,N.再分别以M,N为圆心,适当长度为半径画弧,两弧交于点.连接AP,并延长AP交BC于点.过点作于点,垂足为,则DE的长度为( )
A. B. C.2 D.1
二、填空题
11.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1米,当他把绳子下端拉开5米后,发现下端刚好接触地面,则旗杆高度为 米.
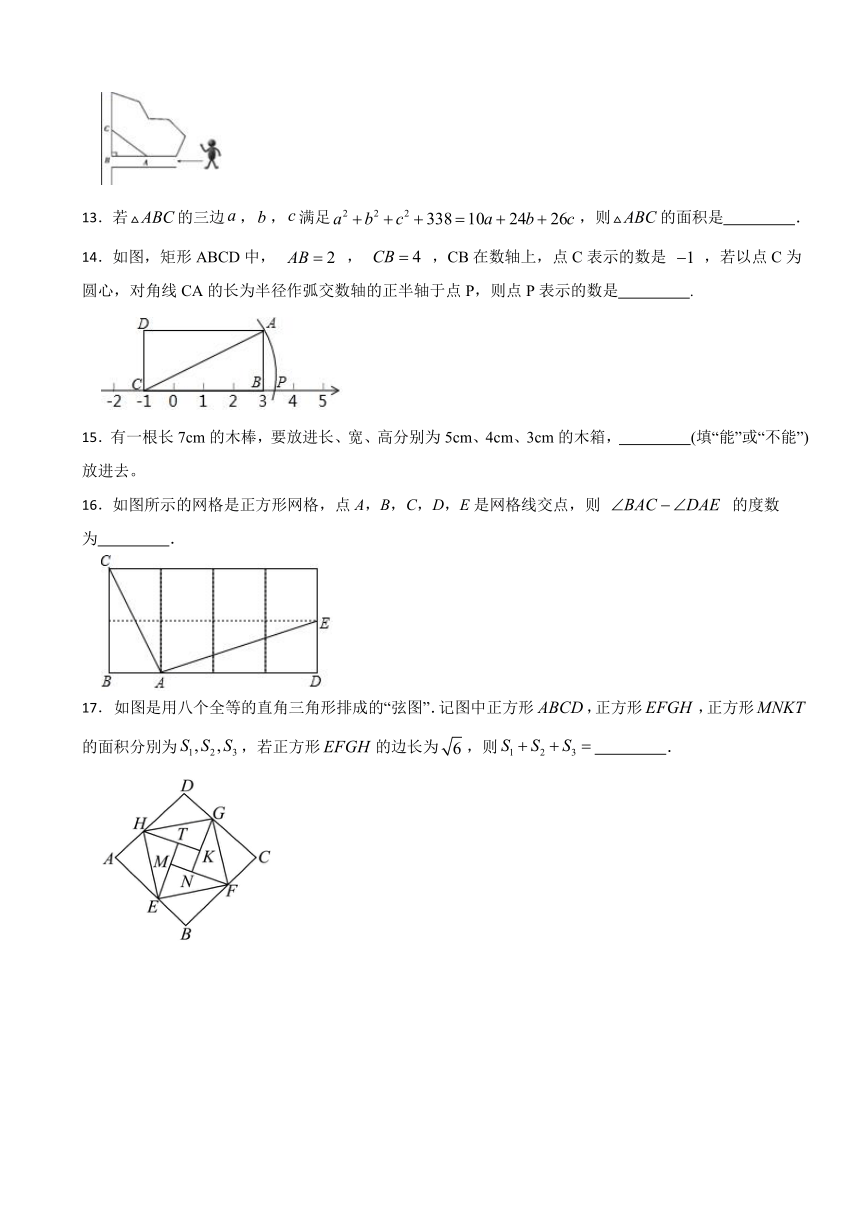
12.下图是公园的一角,有人为了抄近道而避开横平竖直的路的拐角 ,而走“捷径 ”,于是在草坪内走出了一条不该有的“路 ”.已知 米, 米,只为少走 米的路.
13.若的三边,,满足,则的面积是 .
14.如图,矩形ABCD中, , ,CB在数轴上,点C表示的数是 ,若以点C为圆心,对角线CA的长为半径作弧交数轴的正半轴于点P,则点P表示的数是 .
15.有一根长7cm的木棒,要放进长、宽、高分别为5cm、4cm、3cm的木箱, (填“能”或“不能”)放进去。
16.如图所示的网格是正方形网格,点A,B,C,D,E是网格线交点,则 的度数为 .
17. 如图是用八个全等的直角三角形排成的“弦图”.记图中正方形,正方形,正方形的面积分別为,若正方形的边长为,则 .
三、解答题
18.如图,,,,垂足分别为D,E,,.
(1)求的度数;
(2)求线段的长度.
19.如图,在中,于,,,,求的长.
20.如图,有两根长杆隔河相对,一杆DC高3m,另一杆AB高2m,两杆相距BC为5m,两根长杆都与地面垂直,现两杆顶部各有一只鱼鹰,他们同时看到两杆之间的河面上E处浮出一条小鱼,于是同时以同样的速度飞来夺鱼,结果两只鱼鹰同时叼住小鱼,求两杆底部距小鱼的距离各是多少米?(假设小鱼在此过程中保持不变).
21.如图,一辆卡车装满货物后,高4米,宽3米.这辆卡车能通过横截面如图所示(上面是一个半圆,下面是长方形)的隧道吗?
22.如图,飞机在空中水平飞行,某一时刻刚好飞到一男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.飞机每小时飞行多少千米?
23.如图所示,已知△ABC中,∠C=90°,AB=5,BC=3,动点P从点C出发沿C﹣A﹣B以每秒2个单位的速度运动,到达点B时停止运动,设运动时间为t秒(t>0).
(1)AC= .
(2)时,AP的长为 .点P在AB边上时,线段AP的长为 (用含t的代数式表示).
(3)当点P在AB的中垂线上时,求t的值.
(4)如图②,当点P在AB上运动时,连结CP,作点A关于CP的对称点A',连结A'C,A'P.当存在△A'PC的边与△ABC的边平行时,直接写出t的值.
24.图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】B
8.【答案】C
9.【答案】B
10.【答案】A
11.【答案】12
12.【答案】20
13.【答案】30
14.【答案】
15.【答案】能
16.【答案】45°
17.【答案】18
18.【答案】(1)
(2)7
19.【答案】2
20.【答案】3m和2m
21.【答案】解:取半圆的圆心O,使得OB=1.5米,如图.
在Rt△AOB中,由勾股定理得:OB2+AB2 = OA2,
所以1.52+ AB2=2.52,
所以AB=2,
所以AH=AB+BH=2+2.6=4.6,
因为4.6>4,
所以这辆卡车能沿着隧道中间顺利通过.
22.【答案】150m/s
23.【答案】(1)4
(2)3;2t﹣4
(3)解:如图,设的垂直平分线与交于点 ,
∵,
∴,
当点在上时,,
∴,
∴,
∴;
当点与点重合时,,
∴;
综上所述,的值为或;
(4)解:的值为或.
24.【答案】解:⑴将前面、右面展开至一个平面,由勾股定理得AB2=(3+4)2+52=74;
⑵将前面、上面展开至一个平面,由勾股定理得AB2=(3+5)2+42=80;
⑶将左面、上面展开至一个平面,由勾股定理得AB2=(5+4)2+32=90;
所以最短路径长为 cm.
一、单选题
1.学了“勾股定理”后,甲、乙两位同学的观点如下:
甲:如果是直角三角形,那么一定成立;
乙:在中,如果,那么不是直角三角形.
对于两人的观点,下列说法正确的是( )
A.甲对,乙错 B.甲错,乙对 C.两人都错 D.两人都对
2.如图,在中,,分别以,为边向外作正方形,面积分别为,,若,,则的长为( )
A.4 B.2 C. D.3
3.为预防新冠疫情,民生大院入口的正上方处装有红外线激光测温仪(如图所示),测温仪离地面的距离米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为米的市民正对门缓慢走到离门米的地方时(即米),测温仪自动显示体温,则人头顶离测温仪的距离等于( )
A.米 B.米 C.米 D.米
4.如图,矩形ABCD的对角线AC、BD相交于点O,∠ABO=60°,若矩形的对角线长为6.则线段AD的长是( )
A.3 B.4 C.2 D.3
5.如图是一圆柱玻璃杯,从内部测得底面半径为,高为,现有一根长为的吸管任意放入杯中,则吸管露在杯口外的长度最少是( )
A. B. C. D.
6.如图,已知矩形纸片,,,点在边上,将沿折叠,点落在点处,,分别交于点,,且,则的长为( )
A. B. C. D.
7. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
A. B. C. D.2
8.如图,有一个水池,水面是一个边长为尺的正方形,在水池正中央有一根芦苇,它高出水面尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面、求这根芦苇的长度是多少尺?设芦苇的长度是尺,根据题意,可列方程为( )
A. B.
C. D.
9.如图,过矩形对角线的交点,作对角线的垂线,交于点,交于点,若,,则的长等于( )
A. B. C. D.
10.在Rt中,.以为圆心,AM的长为半径作弧,分别交AC,AB于点M,N.再分别以M,N为圆心,适当长度为半径画弧,两弧交于点.连接AP,并延长AP交BC于点.过点作于点,垂足为,则DE的长度为( )
A. B. C.2 D.1
二、填空题
11.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1米,当他把绳子下端拉开5米后,发现下端刚好接触地面,则旗杆高度为 米.
12.下图是公园的一角,有人为了抄近道而避开横平竖直的路的拐角 ,而走“捷径 ”,于是在草坪内走出了一条不该有的“路 ”.已知 米, 米,只为少走 米的路.
13.若的三边,,满足,则的面积是 .
14.如图,矩形ABCD中, , ,CB在数轴上,点C表示的数是 ,若以点C为圆心,对角线CA的长为半径作弧交数轴的正半轴于点P,则点P表示的数是 .
15.有一根长7cm的木棒,要放进长、宽、高分别为5cm、4cm、3cm的木箱, (填“能”或“不能”)放进去。
16.如图所示的网格是正方形网格,点A,B,C,D,E是网格线交点,则 的度数为 .
17. 如图是用八个全等的直角三角形排成的“弦图”.记图中正方形,正方形,正方形的面积分別为,若正方形的边长为,则 .
三、解答题
18.如图,,,,垂足分别为D,E,,.
(1)求的度数;
(2)求线段的长度.
19.如图,在中,于,,,,求的长.
20.如图,有两根长杆隔河相对,一杆DC高3m,另一杆AB高2m,两杆相距BC为5m,两根长杆都与地面垂直,现两杆顶部各有一只鱼鹰,他们同时看到两杆之间的河面上E处浮出一条小鱼,于是同时以同样的速度飞来夺鱼,结果两只鱼鹰同时叼住小鱼,求两杆底部距小鱼的距离各是多少米?(假设小鱼在此过程中保持不变).
21.如图,一辆卡车装满货物后,高4米,宽3米.这辆卡车能通过横截面如图所示(上面是一个半圆,下面是长方形)的隧道吗?
22.如图,飞机在空中水平飞行,某一时刻刚好飞到一男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.飞机每小时飞行多少千米?
23.如图所示,已知△ABC中,∠C=90°,AB=5,BC=3,动点P从点C出发沿C﹣A﹣B以每秒2个单位的速度运动,到达点B时停止运动,设运动时间为t秒(t>0).
(1)AC= .
(2)时,AP的长为 .点P在AB边上时,线段AP的长为 (用含t的代数式表示).
(3)当点P在AB的中垂线上时,求t的值.
(4)如图②,当点P在AB上运动时,连结CP,作点A关于CP的对称点A',连结A'C,A'P.当存在△A'PC的边与△ABC的边平行时,直接写出t的值.
24.图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】B
8.【答案】C
9.【答案】B
10.【答案】A
11.【答案】12
12.【答案】20
13.【答案】30
14.【答案】
15.【答案】能
16.【答案】45°
17.【答案】18
18.【答案】(1)
(2)7
19.【答案】2
20.【答案】3m和2m
21.【答案】解:取半圆的圆心O,使得OB=1.5米,如图.
在Rt△AOB中,由勾股定理得:OB2+AB2 = OA2,
所以1.52+ AB2=2.52,
所以AB=2,
所以AH=AB+BH=2+2.6=4.6,
因为4.6>4,
所以这辆卡车能沿着隧道中间顺利通过.
22.【答案】150m/s
23.【答案】(1)4
(2)3;2t﹣4
(3)解:如图,设的垂直平分线与交于点 ,
∵,
∴,
当点在上时,,
∴,
∴,
∴;
当点与点重合时,,
∴;
综上所述,的值为或;
(4)解:的值为或.
24.【答案】解:⑴将前面、右面展开至一个平面,由勾股定理得AB2=(3+4)2+52=74;
⑵将前面、上面展开至一个平面,由勾股定理得AB2=(3+5)2+42=80;
⑶将左面、上面展开至一个平面,由勾股定理得AB2=(5+4)2+32=90;
所以最短路径长为 cm.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
