2016人教版九年级数学下册教学课件:27.2.2相似三角形的性质(共14张PPT)
文档属性
| 名称 | 2016人教版九年级数学下册教学课件:27.2.2相似三角形的性质(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 84.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-21 00:00:00 | ||
图片预览





文档简介
课件14张PPT。27.2.2相似三角形的性质义务教育教科书(人教版)九年级数学下册
知识回顾相似三角形的判定方法有哪几种?1、对应边成比例,对应角相等的两个三角形相似。2、平行于三角形一边,与另外两边相交所构成的三角形与原
三角形相似。3、SSS4、两边成比例且夹角相等的两个三角形相似。5、AA6、HL情境引入三角形除了三个角,三条边外,还有哪些要素?
思考:如果三角形相似,那么,三角形的这些要素有一些怎样的性质呢?高线角平分线中线面积周长求证:∵ △ABC∽△A’B’C’已知:△ABC∽△A’B’C’,相似比为k,且AD⊥BC,AD⊥BC又 AD⊥BC,AD⊥BC
∴ ∠ADB= ∠A ’D ’B ’=900
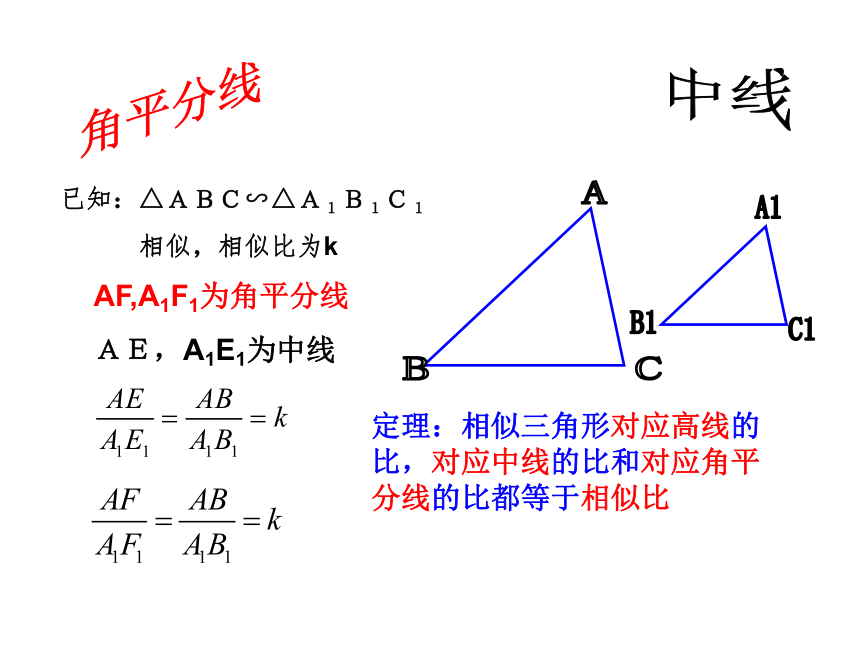
∴证明:性质:相似三角形的高线比等于相似比高线自主预习角平分线中线AF,A1F1为角平分线
AE,A1E1为中线定理:相似三角形对应高线的比,对应中线的比和对应角平分线的比都等于相似比已知:△ABC∽△A1B1C1
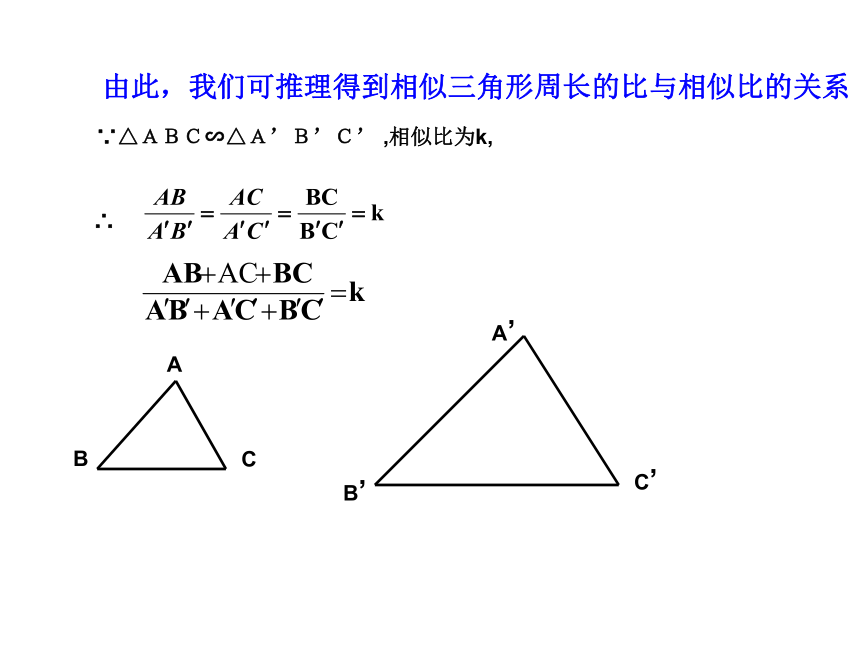
相似,相似比为k∵△ABC∽△A’B’C’ ,相似比为k,∴由此,我们可推理得到相似三角形周长的比与相似比的关系新知探究已知:△ABC∽△A1B1C1
相似,相似比为k定理:相似三角形面积比等于相似比的平方S△A1B1C1= B1C1 A1D1∴且解:例1 如图,在 和 中,AB=2DE,AC=2DF
, ,BC边上的高为6,面积是 ,
求△DEF的边EF上的高和面积。新知探究解:在△ABC和△DEF中,
∵AB=2DE,AC=2DE又 ∠D=∠A∴ △ABC∽ △DEF,相似比为1/2新知探究知识梳理本节课你学习了什么知识?随堂练习1、如果把一个三角形按照下面的条件改成和它相似的三角形:
(1)把边长扩大为原来的100倍,那么面积扩大为原来的多少倍?
(2)把面积扩大为原来的100倍,那么边长扩大为原来的多少倍?2、求三角形的三条中位线所围成的三角形与原三角形的面积的比.随堂练习3、如图,△ABC中,点D、E、F分别在AB、AC、BC上,且DE∥BC,EF∥AB。当D点为AB中点时,求SBFED:S△ABC的值。随堂练习4、如果两个相似三角形的面积之比为1:9,则它们对应边的比为 对应高的比为 。周长的比为
5、如果两个相似三角形的面积之比为2:7,较大三角形一边上的高为 ,则较小三角形对应边上的高为 6、如图,这是圆桌正上方的灯泡(当成一个点)发出
的光线照射桌面形成阴影的示意图,已知桌面的直径
为1.2米,桌面距离地面为1米,若灯泡距离地面3米,
则地面上阴影部分的面积为多少?随堂练习
知识回顾相似三角形的判定方法有哪几种?1、对应边成比例,对应角相等的两个三角形相似。2、平行于三角形一边,与另外两边相交所构成的三角形与原
三角形相似。3、SSS4、两边成比例且夹角相等的两个三角形相似。5、AA6、HL情境引入三角形除了三个角,三条边外,还有哪些要素?
思考:如果三角形相似,那么,三角形的这些要素有一些怎样的性质呢?高线角平分线中线面积周长求证:∵ △ABC∽△A’B’C’已知:△ABC∽△A’B’C’,相似比为k,且AD⊥BC,AD⊥BC又 AD⊥BC,AD⊥BC
∴ ∠ADB= ∠A ’D ’B ’=900
∴证明:性质:相似三角形的高线比等于相似比高线自主预习角平分线中线AF,A1F1为角平分线
AE,A1E1为中线定理:相似三角形对应高线的比,对应中线的比和对应角平分线的比都等于相似比已知:△ABC∽△A1B1C1
相似,相似比为k∵△ABC∽△A’B’C’ ,相似比为k,∴由此,我们可推理得到相似三角形周长的比与相似比的关系新知探究已知:△ABC∽△A1B1C1
相似,相似比为k定理:相似三角形面积比等于相似比的平方S△A1B1C1= B1C1 A1D1∴且解:例1 如图,在 和 中,AB=2DE,AC=2DF
, ,BC边上的高为6,面积是 ,
求△DEF的边EF上的高和面积。新知探究解:在△ABC和△DEF中,
∵AB=2DE,AC=2DE又 ∠D=∠A∴ △ABC∽ △DEF,相似比为1/2新知探究知识梳理本节课你学习了什么知识?随堂练习1、如果把一个三角形按照下面的条件改成和它相似的三角形:
(1)把边长扩大为原来的100倍,那么面积扩大为原来的多少倍?
(2)把面积扩大为原来的100倍,那么边长扩大为原来的多少倍?2、求三角形的三条中位线所围成的三角形与原三角形的面积的比.随堂练习3、如图,△ABC中,点D、E、F分别在AB、AC、BC上,且DE∥BC,EF∥AB。当D点为AB中点时,求SBFED:S△ABC的值。随堂练习4、如果两个相似三角形的面积之比为1:9,则它们对应边的比为 对应高的比为 。周长的比为
5、如果两个相似三角形的面积之比为2:7,较大三角形一边上的高为 ,则较小三角形对应边上的高为 6、如图,这是圆桌正上方的灯泡(当成一个点)发出
的光线照射桌面形成阴影的示意图,已知桌面的直径
为1.2米,桌面距离地面为1米,若灯泡距离地面3米,
则地面上阴影部分的面积为多少?随堂练习
