第1章 一元二次方程 分类提升训练 (含答案)2024--2025学年苏科版九年级数学上册
文档属性
| 名称 | 第1章 一元二次方程 分类提升训练 (含答案)2024--2025学年苏科版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 227.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 10:26:38 | ||
图片预览



文档简介
第1章 一元二次方程 分类提升训练 2024--2025学年苏科版九年级数学上册
一、单选题
1.新能源汽车节能、环保,越来越受消费者喜爱,我国新能源汽车近几年销售量全球第一,年新能源车销量为万辆,销量逐年增加,到年销量为万辆,求这款新能源汽车的年平均增长率是多少?可设年平均增长率为.根据题意可列方程为( ).
A. B.
C. D.
2.在某中学开展的课外阅读活动中,要求七,八、九三个年级学生的人均阅读量逐次增加,而且增长率相同,已知七年级学生的人均阅读量为每年10万字,九年级学生的人均阅读量为每年14.4万字,则该校八年级学生的人均阅读量为每年( )
A.11万字 B.11.2万字 C.12万字 D.12.2万字
3.关于x的一元二次方程有实数根,则m的最小整数值为( )
A.1 B.0 C. D.
4.用配方法解一元二次方程x2-8x+5=0,将其化成(x+a)2=b的形式,则变形正确的是( )
A.(x - 4)2=11 B.(x-4)2=21 C.(x -8)2=11 D.(x+4)2=11
5.已知x1,x2是一元二次方程x2+3x 1=0的两个实数根,则x22+2x2 x1的值为( )
A.4 B.1 C.-2 D.-1
6.方程(x+1)(x-3)=5的解是 ( )
A.x1=1,x2=3 B.x1=4, x2=-2
C.x1=-1, x2 =3 D.x1=-4, x2=2
7.已知,则的值是( )
A.或1 B.或 C.或 D.或2
8.方程 的解是( )
A. B. C. D.
9.若关于x的一元二次方程有两个相等的实数根,则实数a的值为( )
A.2 B.-2 C.-2或6 D.-6或2
10.如图,直线y=x+6与反比例函数y=的图象相交于点C,D,与坐标轴相分别交于点A,B,作CE⊥y轴于点E,作DF⊥y轴于点F,过点E,F分别作EM∥AB,FN∥AB,分别交x轴于点M,N,线段DF与EM相交于点P.有以下说法:
①CEPD的面积等于PFNM的面积;
②CE=ON=BM;
③若CEPD与PFNM的面积和为12,则k=12.
其中正确的说法是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
11.将方程x2﹣2=7x化成x2+bx+c=0的形式、则一次项是 ,b+c= .
12.若x1,x2是方程 的两个实数根,则代数式 的值等于 .
13.若一元二次方程有两个相等的实数根,则m= .
14.已知是方程的两个不等的实数根,则的值为 .
15.将关于x的一元二次方程变形为,就可以将表示为关于x的一次多项式,从而达到“降次”的目的,又如…,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知:,且.则的值为 .
16.如图,平面直角坐标系中,函数的图象经过,两点.若的面积为6,则的值为 .
三、解答题
17.新年到了,为增进同学友谊,某班主任规定本班同学间,每两个人必须相互通电话1次
(1)若本班人数为20,则共通话________次,若本班人数为(,且为正整数),则共通话________次;
(2)若同学们共通话1225次,求该班同学的人数;
(3)王峰同学由打电话问题想到了一个数学问题:若线段上共有个点(不含端点、),线段总数为多少呢?请直接写出结论.
18.已知关于的方程.
(1)当时,求原方程的解.
(2)若原方程有两个相等的实数根,求的值.
19.某商店经销的某种商品,每件成本为40元.经市场调研,售价为50元时,可销售200件;售价每增加 元,销售量将减少10件.如果这种商品全部销售完,那么该商店可盈利2000元.问:该商店销售了这种商品多少件?每件售价多少元?
20.若关于x的一元二次方程x2﹣4x+k﹣3=0的两个实数根为x1、x2,且满足x1=3x2,试求出方程的两个实数根及k的值.
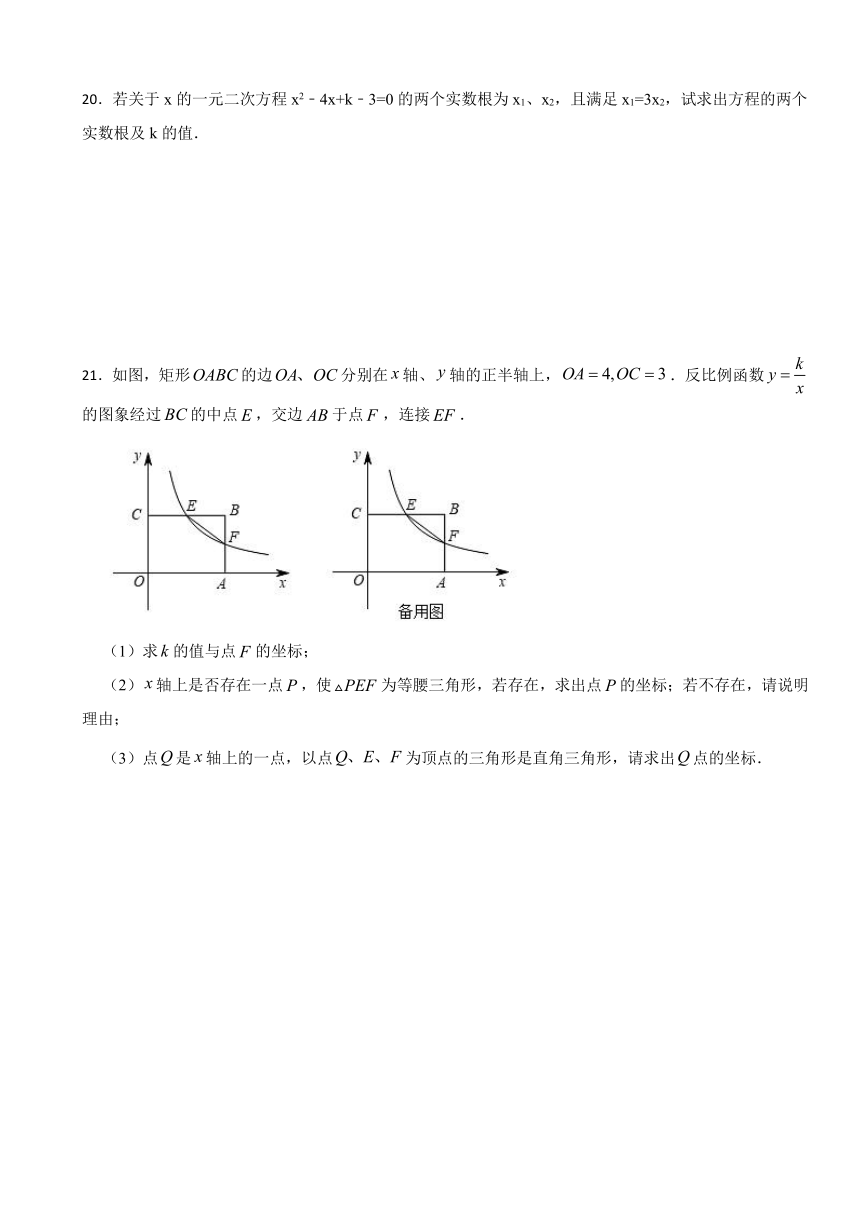
21.如图,矩形的边分别在轴、轴的正半轴上,.反比例函数的图象经过的中点,交边于点,连接.
(1)求的值与点的坐标;
(2)轴上是否存在一点,使为等腰三角形,若存在,求出点的坐标;若不存在,请说明理由;
(3)点是轴上的一点,以点为顶点的三角形是直角三角形,请求出点的坐标.
22.有一块长为a米,宽为b米的长方形场地,计划在该场地上修建宽均为x米的两条互相垂直的道路,余下的四块长方形场地建成草坪.
(1)已知,且四块草坪的面积和为264平方米,则每条道路的宽x为多少米?
(2)若,且四块草坪的面积和为264平方米,则原来矩形场地的长和宽各为多少米?
(3)已知,现要在场地上修建若干条宽均为2米的纵横小路,假设有m条水平方向的小路,n条竖直方向的小路(其中,m,n为常数),使草坪地的总面积为132平方米,则 (直接写出答案).
23.新定义:若实数m,n满足时,就称点为“雅隽致远点”.
(1)判断点、是不是“雅隽致远点”?
(2)若反比例函数的图象上存在两个不同的“雅隽致远点”A,B,且,求出反比例函数的解析式;
(3)已知抛物线上存在唯一的“雅隽致远点”,且当时,s的最小值为,求t值.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】A
5.【答案】A
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】C
10.【答案】A
11.【答案】-7x;-9
12.【答案】2028
13.【答案】2
14.【答案】1
15.【答案】
16.【答案】
17.【答案】(1)190,
(2)50人
(3)
18.【答案】(1),
(2)
19.【答案】解:设每件商品售价为x元,则销售量为[200 10(x 50)]件,
由题意得:(x 40)[200 10(x 50)]=2000,
整理得:x2 110x+3000=0,
解得x1=60,x2=50.
当x=60时,销售量为:200 10(x 50)=200 10(60 50)=100(件);
当x=50时,销售量为:200件.
答:该商店销售了这种商品100或200件,每件售价为60或50元。
20.【答案】解:由根与系数的关系,得
x1+x2=4 ,
x1 x2=k﹣3
又∵x1=3x2
∴x1=3,x2=1;
∴k=x1x2+3=3×1+3=6
答:方程两根为x1=3,x2=1;k=6.
21.【答案】(1),
(2)存在,或
(3)或
22.【答案】(1)解:四块矩形场地可合成长为米,宽为米的长方形.
依题意得:,
整理得:,
解得:(不合题意,舍去).
答:每条道路的宽x为2米.
(2)解:,
,
又道路的宽度米,
四块矩形场地可合成长为米,宽为米的长方形.
依题意得:,
整理得:,
解得:(不合题意,舍去),
.
答:原来矩形场地的长为26米,宽为13米.
(3)25
23.【答案】(1)不是“雅隽致远点”;不是“雅隽致远点”
(2)
(3)或
一、单选题
1.新能源汽车节能、环保,越来越受消费者喜爱,我国新能源汽车近几年销售量全球第一,年新能源车销量为万辆,销量逐年增加,到年销量为万辆,求这款新能源汽车的年平均增长率是多少?可设年平均增长率为.根据题意可列方程为( ).
A. B.
C. D.
2.在某中学开展的课外阅读活动中,要求七,八、九三个年级学生的人均阅读量逐次增加,而且增长率相同,已知七年级学生的人均阅读量为每年10万字,九年级学生的人均阅读量为每年14.4万字,则该校八年级学生的人均阅读量为每年( )
A.11万字 B.11.2万字 C.12万字 D.12.2万字
3.关于x的一元二次方程有实数根,则m的最小整数值为( )
A.1 B.0 C. D.
4.用配方法解一元二次方程x2-8x+5=0,将其化成(x+a)2=b的形式,则变形正确的是( )
A.(x - 4)2=11 B.(x-4)2=21 C.(x -8)2=11 D.(x+4)2=11
5.已知x1,x2是一元二次方程x2+3x 1=0的两个实数根,则x22+2x2 x1的值为( )
A.4 B.1 C.-2 D.-1
6.方程(x+1)(x-3)=5的解是 ( )
A.x1=1,x2=3 B.x1=4, x2=-2
C.x1=-1, x2 =3 D.x1=-4, x2=2
7.已知,则的值是( )
A.或1 B.或 C.或 D.或2
8.方程 的解是( )
A. B. C. D.
9.若关于x的一元二次方程有两个相等的实数根,则实数a的值为( )
A.2 B.-2 C.-2或6 D.-6或2
10.如图,直线y=x+6与反比例函数y=的图象相交于点C,D,与坐标轴相分别交于点A,B,作CE⊥y轴于点E,作DF⊥y轴于点F,过点E,F分别作EM∥AB,FN∥AB,分别交x轴于点M,N,线段DF与EM相交于点P.有以下说法:
①CEPD的面积等于PFNM的面积;
②CE=ON=BM;
③若CEPD与PFNM的面积和为12,则k=12.
其中正确的说法是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
11.将方程x2﹣2=7x化成x2+bx+c=0的形式、则一次项是 ,b+c= .
12.若x1,x2是方程 的两个实数根,则代数式 的值等于 .
13.若一元二次方程有两个相等的实数根,则m= .
14.已知是方程的两个不等的实数根,则的值为 .
15.将关于x的一元二次方程变形为,就可以将表示为关于x的一次多项式,从而达到“降次”的目的,又如…,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知:,且.则的值为 .
16.如图,平面直角坐标系中,函数的图象经过,两点.若的面积为6,则的值为 .
三、解答题
17.新年到了,为增进同学友谊,某班主任规定本班同学间,每两个人必须相互通电话1次
(1)若本班人数为20,则共通话________次,若本班人数为(,且为正整数),则共通话________次;
(2)若同学们共通话1225次,求该班同学的人数;
(3)王峰同学由打电话问题想到了一个数学问题:若线段上共有个点(不含端点、),线段总数为多少呢?请直接写出结论.
18.已知关于的方程.
(1)当时,求原方程的解.
(2)若原方程有两个相等的实数根,求的值.
19.某商店经销的某种商品,每件成本为40元.经市场调研,售价为50元时,可销售200件;售价每增加 元,销售量将减少10件.如果这种商品全部销售完,那么该商店可盈利2000元.问:该商店销售了这种商品多少件?每件售价多少元?
20.若关于x的一元二次方程x2﹣4x+k﹣3=0的两个实数根为x1、x2,且满足x1=3x2,试求出方程的两个实数根及k的值.
21.如图,矩形的边分别在轴、轴的正半轴上,.反比例函数的图象经过的中点,交边于点,连接.
(1)求的值与点的坐标;
(2)轴上是否存在一点,使为等腰三角形,若存在,求出点的坐标;若不存在,请说明理由;
(3)点是轴上的一点,以点为顶点的三角形是直角三角形,请求出点的坐标.
22.有一块长为a米,宽为b米的长方形场地,计划在该场地上修建宽均为x米的两条互相垂直的道路,余下的四块长方形场地建成草坪.
(1)已知,且四块草坪的面积和为264平方米,则每条道路的宽x为多少米?
(2)若,且四块草坪的面积和为264平方米,则原来矩形场地的长和宽各为多少米?
(3)已知,现要在场地上修建若干条宽均为2米的纵横小路,假设有m条水平方向的小路,n条竖直方向的小路(其中,m,n为常数),使草坪地的总面积为132平方米,则 (直接写出答案).
23.新定义:若实数m,n满足时,就称点为“雅隽致远点”.
(1)判断点、是不是“雅隽致远点”?
(2)若反比例函数的图象上存在两个不同的“雅隽致远点”A,B,且,求出反比例函数的解析式;
(3)已知抛物线上存在唯一的“雅隽致远点”,且当时,s的最小值为,求t值.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】A
5.【答案】A
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】C
10.【答案】A
11.【答案】-7x;-9
12.【答案】2028
13.【答案】2
14.【答案】1
15.【答案】
16.【答案】
17.【答案】(1)190,
(2)50人
(3)
18.【答案】(1),
(2)
19.【答案】解:设每件商品售价为x元,则销售量为[200 10(x 50)]件,
由题意得:(x 40)[200 10(x 50)]=2000,
整理得:x2 110x+3000=0,
解得x1=60,x2=50.
当x=60时,销售量为:200 10(x 50)=200 10(60 50)=100(件);
当x=50时,销售量为:200件.
答:该商店销售了这种商品100或200件,每件售价为60或50元。
20.【答案】解:由根与系数的关系,得
x1+x2=4 ,
x1 x2=k﹣3
又∵x1=3x2
∴x1=3,x2=1;
∴k=x1x2+3=3×1+3=6
答:方程两根为x1=3,x2=1;k=6.
21.【答案】(1),
(2)存在,或
(3)或
22.【答案】(1)解:四块矩形场地可合成长为米,宽为米的长方形.
依题意得:,
整理得:,
解得:(不合题意,舍去).
答:每条道路的宽x为2米.
(2)解:,
,
又道路的宽度米,
四块矩形场地可合成长为米,宽为米的长方形.
依题意得:,
整理得:,
解得:(不合题意,舍去),
.
答:原来矩形场地的长为26米,宽为13米.
(3)25
23.【答案】(1)不是“雅隽致远点”;不是“雅隽致远点”
(2)
(3)或
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
