22.3实际问题与二次函数预习检测卷(含解析)-数学九年级上册人教版
文档属性
| 名称 | 22.3实际问题与二次函数预习检测卷(含解析)-数学九年级上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 18:06:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
22.3实际问题与二次函数预习检测卷-数学九年级上册人教版
一、单选题
1.飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是.飞机滑行多长时间才能停下来 ( )
A.18s B.10s C.20s D.15s
2.一个球从地面竖直向上弹起,球距离地面的高度(单位:米)与经过的时间(单位:秒)满足函数关系式,那么球弹起后又回到地面所经过的时间是( )
A.4秒 B.3秒 C.2秒 D.1秒
3.深高小学部饲养了两只萌萌的羊驼,建筑队在学校一边靠墙处,计划用15米长的铁栅栏围成三个相连的长方形羊驼草料仓库,仓库总面积为平方米,为方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门,若设米,则关于x的函数关系式为( )
A. B. C. D.
4.如图,以某速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球在时落地,小球的飞行高度(单位:)与飞行时间(单位:)之间具有函数关系(为常数,).有下列结论:
①值为;
②小球的飞行高度最高可达到;
③小球有两个飞行的时间使小球的高度刚好达到.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
5.如图,人民医院在某流感高发时段,用防护隔帘布临时搭建了一隔离区,隔离区一面靠长为的墙,隔离区分成两个区域,中间也用防护隔帘布隔开.已知整个隔离区所用防护隔帘布总长为,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长,小明认为:隔离区的最大面积为;小亮认为:隔离区的面积可能为.你认为他们俩的说法是( )
A.小明正确,小亮错误 B.小明错误,小亮正确
C.两人均正确 D.两人均错误
6.某公司计划生产一种新型电子产品,经过公司测算,在生产数量不超过8万件的情况下,生产成本和销售价格均是生产数量的一次函数,其部分数据如下表:
生产数量(万件) 生产成本(元/件) 销售价格(元/件)
1 9 16
2 8 14
3 7 12
为获最大利润,生产数量应为( )
A.3万件 B.4万件 C.5万件 D.6万件
7.如图,在中,,,,点 P 从点A 出发,沿向点C 以的速度运动,同时点 Q从点C 出发,沿向点B 以的速度运动(当点 Q 运动到点 B 时,点 P,Q 同时停止运动).在运动过程中,四边形的面积最小为( )
A. B. C. D.
8.刀削面堪称天下一绝,传统的操作方法是一手托面,一手拿刀,直接将面削到开水锅里.如图,面刚被削离时与开水锅的高度差,与锅的水平距离,锅的半径.若将削出的小面圈的运动轨迹视为抛物线的一部分,要使其落入锅中(锅的厚度忽略不计),则其水平初速度不可能为(提示:,,水平移动距离)( )
A. B. C. D.
二、填空题
9.用长度一定的绳子围成一个矩形,如果矩形的一边长(单位:)与面积(单位:满足函数解析式,则矩形的面积的最大值为 .
10.小汽车刹车距离与速度之间的函数关系式为,一辆小汽车正以的速度匀速行驶,若前方处停放一辆故障车,此时刹车 (填“会”或“不会”)撞上前面的故障车.
11.某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲,宾馆需为有游客居住的房间每天支出20元费用,若想要获得最大利润,则房价应定为每个房间每天 元.
12.如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 则铅球被推出的水平距离为 m.
13.在为期3天的广安市第五届运动会(青少年组)三人制篮球比赛中,某同学进行了一次投篮,篮球准确落入篮框内,建立如图所示的平面直角坐标系,篮球的运行轨迹可看作抛物线的一部分,则篮球在空中运行的最大高度为 .
14.某同学参加航模设计制作比赛,其设计的火箭升空高度(单位:)与飞行时间(单位:s)满足关系,当火箭升空到最高点时,距离地面 .
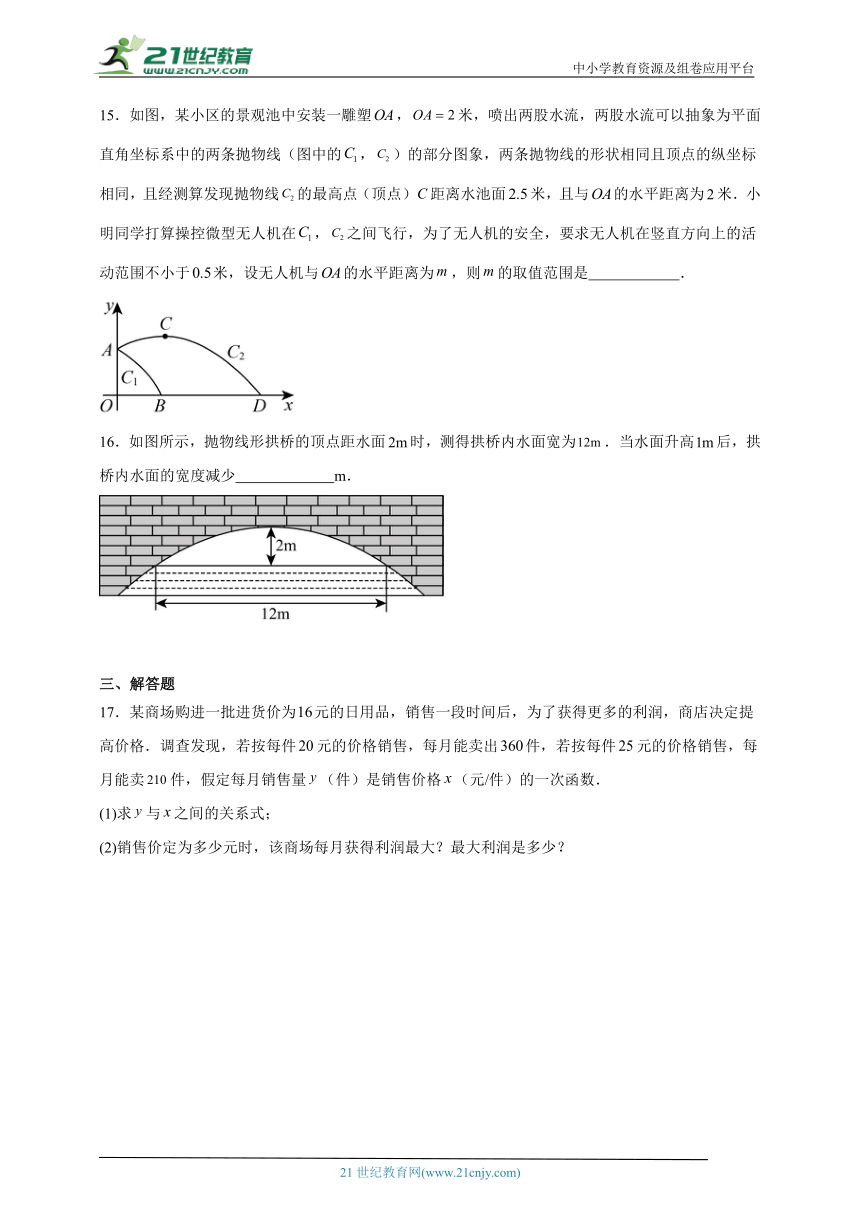
15.如图,某小区的景观池中安装一雕塑,米,喷出两股水流,两股水流可以抽象为平面直角坐标系中的两条抛物线(图中的,)的部分图象,两条抛物线的形状相同且顶点的纵坐标相同,且经测算发现抛物线的最高点(顶点)距离水池面米,且与的水平距离为米.小明同学打算操控微型无人机在,之间飞行,为了无人机的安全,要求无人机在竖直方向上的活动范围不小于米,设无人机与的水平距离为,则的取值范围是 .
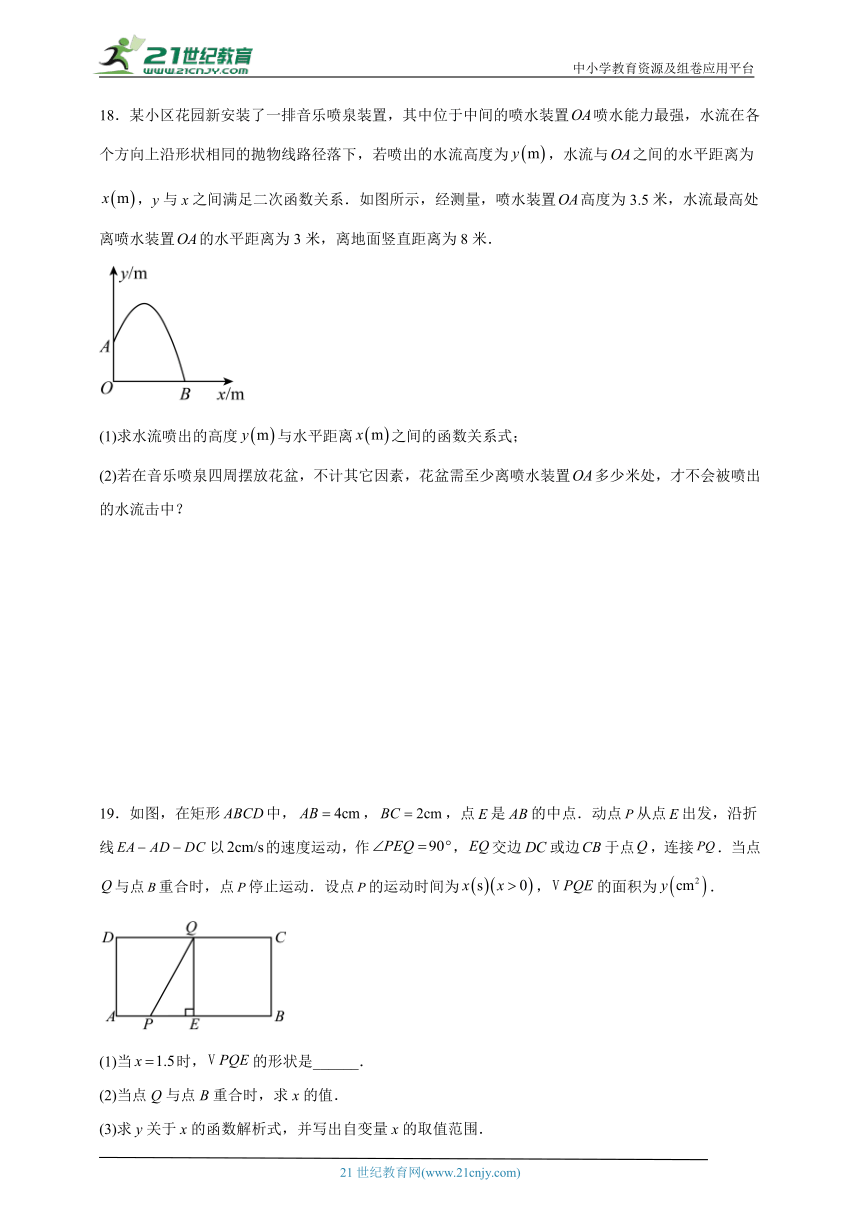
16.如图所示,抛物线形拱桥的顶点距水面时,测得拱桥内水面宽为.当水面升高后,拱桥内水面的宽度减少 m.
三、解答题
17.某商场购进一批进货价为元的日用品,销售一段时间后,为了获得更多的利润,商店决定提高价格.调查发现,若按每件元的价格销售,每月能卖出件,若按每件元的价格销售,每月能卖件,假定每月销售量(件)是销售价格(元/件)的一次函数.
(1)求与之间的关系式;
(2)销售价定为多少元时,该商场每月获得利润最大?最大利润是多少?
18.某小区花园新安装了一排音乐喷泉装置,其中位于中间的喷水装置喷水能力最强,水流在各个方向上沿形状相同的抛物线路径落下,若喷出的水流高度为,水流与之间的水平距离为,y与x之间满足二次函数关系.如图所示,经测量,喷水装置高度为3.5米,水流最高处离喷水装置的水平距离为3米,离地面竖直距离为8米.
(1)求水流喷出的高度与水平距离之间的函数关系式;
(2)若在音乐喷泉四周摆放花盆,不计其它因素,花盆需至少离喷水装置多少米处,才不会被喷出的水流击中?
19.如图,在矩形中,,,点是的中点.动点从点出发,沿折线以的速度运动,作,交边或边于点,连接.当点与点重合时,点停止运动.设点的运动时间为,的面积为.
(1)当时,的形状是______.
(2)当点Q与点B重合时,求x的值.
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
20.如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同,正常水位时,大孔水面宽度米,顶点距水面米(即米),小孔顶点距水面米(即米),当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度.
21.在文艺汇演来临之际,九年级2班同学准备装饰教室.他们在相对的两面墙上的B,C两点之间拉了一根彩带,彩带自然下垂后呈抛物线形,地面上两点O,D分别在点B,C的正下方,已知米,和之间的水平距离为10米.以所在直线为y轴,所在直线为x轴建立如图1所示的平面直角坐标系,此时彩带自然下垂形状可近似看作抛物线.
(1)求该抛物线的函数表达式及彩带到地面的最小距离.
(2)为了使彩带的造型美观,现将图1中彩带最低点固定在灯E上(灯宽度、厚度不计,图中所有点均在同一竖直平面内),且灯E到和的距离相等,这样灯E两侧的彩带就形成了两个对称的新抛物线,如图2所示.若两个新抛物线最低点之间的水平距离为4米,且灯E到地面的距离为2.7米,则图2中彩带最低点比之前升高了多少米?
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C B A C B B C D
1.C
【分析】本题考查了二次函数在实际问题中的应用.将函数解析式写成顶点式,然后根据二次函数的性质可得答案.
【详解】解:
,
∵,
∴当时,s取最大值,且最大值是600.
即飞机滑行才能停下来.
故选:C.
2.B
【分析】本题考查二次函数的实际应用,掌握二次函数的性质,是解题的关键.令,求出的值即可.
【详解】解:∵,
∴当时,即:,
解得:或,
∴球弹起后又回到地面所经过的时间是3秒.
故选:B.
3.A
【分析】本题考查了根据实际问题列二次函数关系式,由铁栅栏的全长及的长,可得出平行于墙的一边长为米,再利用长方形的面积公式,即可找出y关于x的函数关系式.
【详解】解:铁栅栏的全长为15米,米,
平行于墙的一边长为米.
根据题意得:.
故选:A
4.C
【分析】本题考查了二次函数的应用.根据二次函数的图象与性质,分析即可得到答案.
【详解】解:由题意得,解得,①结论正确;
函数关系,
∵,
∴小球的飞行高度最高可达到,②结论错误;
解方程,
得或,
∴小球有两个飞行的时间使小球的高度刚好达到,③结论正确.
故选:C.
5.B
【分析】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握二次函数的性质是解题的关键.设垂直于墙的一边为,则隔离区的另一边为,根据矩形的面积公式列出面积关于的函数解析式,再根据题意求出的取值范围,然后分别令和,解方程求出,取在取值范围内的值即可.
【详解】解:设垂直于墙的一边为,则隔离区的另一边为,
;
根据题意,得不等式组,
解得:,
当时,,
解得(不合题意,舍去);
当时,,
解得,(不合题意,舍去),
故小亮说法正确.
故选:B.
6.B
【分析】本题考查二次函数的应用.根据生产成本和销售价格均是生产数量的一次函数以及表格中的数据,得到生产成本和销售价格的表达式,进而根据利润每件产品的利润生产数量,把相关数值代入可生产利润得关于生产数量的二次函数,进而根据二次函数的性质可得生产数量为多少时,利润最大.
【详解】解:设生产数量为万件,生产成本为元件,销售价格为元件.
生产成本和销售价格均是生产数量的一次函数,
设,.
,符合,
,
解得:.
.
,符合,
.
解得:.
.
设生产利润为,则
.
,
当时,利润最大,
即为获最大利润,生产数量应为4万件.
故选:B.
7.C
【分析】本题考查了二次函数的应用,勾股定理,列函数关系是解题的关键.
先根据勾股定理求出的长,再设点 P 运动时间为t,四边形的面积为y,根据题意表示出y与t的函数关系式,进一步利用二次函数的性质即可求解.
【详解】解:由题可知,是直角三角形,
∴,
设点 P 运动时间为t,四边形的面积为y,
则,
∴,
则当时,y最小为.
故选:C.
8.D
【分析】本题考查了二次函数的应用,要使其落入锅中,需要满足,由即可求解;找出的取值范围是解题的关键.
【详解】解:由题意得
,
解得:,(舍去),
要使其落入锅中,
,
,
,
,
,
不可能;
故选:D.
9.121
【分析】本题主要考查了图形和二次函数的问题,根据二次函数的性质解题即可.
【详解】解:由函数关系可知,
∵二次函数的二次项系数即,
∴当时,y最大值.
故答案为:121.
10.不会
【分析】本题考查二次函数的实际应用,将代入函数解析式,求出刹车距离,进行判断即可.
【详解】解:∵,
∴当时,,
∵,
∴此时刹车不会撞上前面的故障车;
故答案为:不会.
11.
【分析】本题主要考查二次函数的应用,找准等量关系是解题的关键.根据题意列出二次函数,利用二次函数的性质解题即可.
【详解】解:设房价定为元,每天的利润为元,
,
,
,
因为,
故当时,获得最大利润.
故答案为:.
12.9
【分析】本题主要考查了二次函数的应用.依据题意,令,得到关于的方程,解方程即可得出结论.
【详解】解:令,则,
解得:或(不合题意,舍去),
,
.
故答案为:9.
13.3.6//
【分析】本题主要考查了二次函数的应用,熟练掌握二次函数的图像与性质是解题关键.将抛物线解析式转化为顶点式,即可获得答案.
【详解】解:∵,
∴当时,取最大值,最大值为,
即篮球在空中运行的最大高度为.
故答案为:3.6.
14.54
【分析】本题考查了二次函数的应用,直接利用配方法将化为顶点式,进而求解即可,熟练掌握配方法是解题的关键.
【详解】由题意得,
∵,
∴抛物线开口向下,
∴当时,h取最大值,
∴当火箭升空到最高点时,距离地面,
故答案为:54.
15.
【分析】本题考查二次函数的应用,根据题意正确求出函数的解析式是解题关键.
先由题意可知抛物线过点,顶点为点,用待定系数法可求得解析式;再根据两条抛物线的形状相同且顶点的纵坐标相同且经过点,设的解析式为,代入相关数据即可求得解析式,再根据题意进行取舍即可;设无人机的横坐标为,根据题意列出不等式:和,求解即可.
【详解】解:由已知可得:抛物线过点,,
设其解析式为,
把代入得:,
解得,
,
抛物线的解析式为:,
令时,,,
∴,
由两条抛物线的形状相同,设的解析式为,
已知经过点,
∴的解析式为,
两条抛物线顶点的纵坐标相同,
,
解得,
的解析式为①或②,
当时,
①,解得,,;
②,解得,,;
由图可知的顶点的横坐标小于,故舍去①,
的解析式为,
∴,
由题意可得:,
解得:,
又,
解得:,
,
故答案为:.
16.
【分析】本题考查扫物线的性质及应用,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,是中档题.
建立平面直角直角坐标系,设抛物线方程为,由题意知抛物线的顶点坐标是,且抛物线经过点,求出抛物线方程为.由此能求出结果.
【详解】建立如图所示的平面直角坐标系,
设抛物线为,
由题意知抛物线的顶点坐标是,且抛物线经过点,
解得:
∴抛物线方程为.
当水面升高后,,则,解得.
∴当水面升高后,拱桥内水面宽度是米.
当水面升高后,拱桥内水面的宽度减少m.
故答案为:.
17.(1);
(2)销售价定为元时,该商场每月获得利润最大,最大利润是元.
【分析】本题考查二次函数的应用能力,理解题意找到题目的等量关系列出函数关系式是解题的关键;
(1)根据题意利用待定系数法求函数解析式;
(2)根据月利润单件利润月销量列出函数解析式,根据函数的性质求最值即可;
【详解】(1)解:(1)设与之间的关系式为,
根据题意得:,
解得:,
则与之间的函数关系式为;
(2)设利润元,则与的函数关系式是:
,
,
当时,有最大值,最大值为,
销售价定为元时,该商场每月获得利润最大,最大利润是元;
18.(1)
(2)7米
【分析】本题考查二次函数的顶点式,以及二次函数的应用,理解题意是关键.
(1)依据题意得,抛物线的顶点为,从而可设抛物线为,又抛物线过,进而计算可以得解;
(2)依据题意,由抛物线为,进而令,则,求出x的值即可判断得解.
【详解】(1)由题意得,抛物线的顶点为,
∴可设抛物线为.
又抛物线过,
∴.
∴.
∴水流喷出的高度与水平距离之间的函数关系式为.
(2)由题意,∵抛物线为,
∴令,则.
∴或(不合题意,舍去).
∴花盆需至少离喷水装置为7米处,才不会被喷出的水流击中.
19.(1)等腰直角三角形
(2)3
(3)当时,;当时,;当时,
【分析】(1)由题意得出当时,点在上,如图,作于,则,证明,得出,即可得证;
(2)求出当点与点重合时,此时点的运动的距离为,计算即可得出答案;
(3)分三个阶段:当时,点在上运动;当时,点在上运动,作于;当时,点在上运动,作于,分别利用矩形的判定与性质、三角形全等的判定与性质、勾股定理、三角形面积公式计算即可得出答案.
【详解】(1)解:当时,点运动的距离为:,
∵四边形是矩形,
∴,,,
∵点是的中点.
∴,
∴当时,点在中点上,
如图,作于,则,
∴四边形为矩形,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴的形状是等腰直角三角形;
(2)如图,当点与点重合时,
∵,
∴四边形是矩形,
∴,
∴,
∴此时点的运动的距离为,
∴;
(3)∵四边形是矩形,
∴,,,
∵点是的中点.
∴,
如图,当时,点在上运动,
,
此时,
∵,
∴四边形是矩形,
∴,
∴;
如图,当时,点在上运动,作于,则,
∴四边形为矩形,
∴,
同(1)可得,,
∴,
∴的形状是等腰直角三角形,
由题意得:,
∴,
∴,
∴;
如图,当时,点在上运动,作于,
同理可得:四边形为矩形,,
∴,,,
∵,
∴,
∴,
∴,
∴,
∴,
综上所述,.
【点睛】本题考查了矩形的判定与性质、三角形全等的判定与性质、勾股定理、等腰直角三角形的判定与性质,二次函数的应用等知识点,熟练掌握以上知识点并灵活运用,添加适当的辅助线,采用分类讨论的思想是解此题的关键.
20.米
【分析】此题主要考查的是待定系数法求解析式以及二次函数的对称性,求出二次函数的解析式是解决问题的关键;
设出大孔抛物线的解析式的一般形式,代入点的坐标求得函数解析式,再由点的纵坐标代入即可解答.
【详解】解:设大孔对应的抛物线解析式为:,依题意得,,
,
解得:,
即,
当时,,
解得:,
,,
即此时大孔的水面宽度为米
21.(1)抛物线的函数表达式为,彩带到地面的最小距离为2.25米
(2)图2中彩带最低点比之前升高了0.21米
【分析】本题主要考查了二次函数的应用,解题时要熟练掌握并能灵活运用二次函数的性质解题是关键.
(1)依据题意,可知抛物线的对称轴为直线,且过点,,进而可得,故可得,从而可得函数的解析式,当时,,进而可以判断得解;
(2)依据题意,由两个新抛物线对称,且最低点之间的水平距离为4米,可得左边的新抛物线的对称轴为直线,再设左边的新抛物线的函数表达式为,又,,进而求出解析式后即可判断得解.
【详解】(1)由题意,可知抛物线的对称轴为直线,且过点,且,
∴,
∴.
∴抛物线的函数表达式为.
当时,,
∴彩带到地面的最小距离为2.25米.
(2)∵两个新抛物线对称,且最低点之间的水平距离为4米,
∴左边的新抛物线的对称轴为直线.
设左边的新抛物线的函数表达式为.
由题意,可知,.
把,代入中,
得
解得
(米).
答:图2中彩带最低点比之前升高了0.21米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
22.3实际问题与二次函数预习检测卷-数学九年级上册人教版
一、单选题
1.飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是.飞机滑行多长时间才能停下来 ( )
A.18s B.10s C.20s D.15s
2.一个球从地面竖直向上弹起,球距离地面的高度(单位:米)与经过的时间(单位:秒)满足函数关系式,那么球弹起后又回到地面所经过的时间是( )
A.4秒 B.3秒 C.2秒 D.1秒
3.深高小学部饲养了两只萌萌的羊驼,建筑队在学校一边靠墙处,计划用15米长的铁栅栏围成三个相连的长方形羊驼草料仓库,仓库总面积为平方米,为方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门,若设米,则关于x的函数关系式为( )
A. B. C. D.
4.如图,以某速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球在时落地,小球的飞行高度(单位:)与飞行时间(单位:)之间具有函数关系(为常数,).有下列结论:
①值为;
②小球的飞行高度最高可达到;
③小球有两个飞行的时间使小球的高度刚好达到.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
5.如图,人民医院在某流感高发时段,用防护隔帘布临时搭建了一隔离区,隔离区一面靠长为的墙,隔离区分成两个区域,中间也用防护隔帘布隔开.已知整个隔离区所用防护隔帘布总长为,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长,小明认为:隔离区的最大面积为;小亮认为:隔离区的面积可能为.你认为他们俩的说法是( )
A.小明正确,小亮错误 B.小明错误,小亮正确
C.两人均正确 D.两人均错误
6.某公司计划生产一种新型电子产品,经过公司测算,在生产数量不超过8万件的情况下,生产成本和销售价格均是生产数量的一次函数,其部分数据如下表:
生产数量(万件) 生产成本(元/件) 销售价格(元/件)
1 9 16
2 8 14
3 7 12
为获最大利润,生产数量应为( )
A.3万件 B.4万件 C.5万件 D.6万件
7.如图,在中,,,,点 P 从点A 出发,沿向点C 以的速度运动,同时点 Q从点C 出发,沿向点B 以的速度运动(当点 Q 运动到点 B 时,点 P,Q 同时停止运动).在运动过程中,四边形的面积最小为( )
A. B. C. D.
8.刀削面堪称天下一绝,传统的操作方法是一手托面,一手拿刀,直接将面削到开水锅里.如图,面刚被削离时与开水锅的高度差,与锅的水平距离,锅的半径.若将削出的小面圈的运动轨迹视为抛物线的一部分,要使其落入锅中(锅的厚度忽略不计),则其水平初速度不可能为(提示:,,水平移动距离)( )
A. B. C. D.
二、填空题
9.用长度一定的绳子围成一个矩形,如果矩形的一边长(单位:)与面积(单位:满足函数解析式,则矩形的面积的最大值为 .
10.小汽车刹车距离与速度之间的函数关系式为,一辆小汽车正以的速度匀速行驶,若前方处停放一辆故障车,此时刹车 (填“会”或“不会”)撞上前面的故障车.
11.某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲,宾馆需为有游客居住的房间每天支出20元费用,若想要获得最大利润,则房价应定为每个房间每天 元.
12.如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 则铅球被推出的水平距离为 m.
13.在为期3天的广安市第五届运动会(青少年组)三人制篮球比赛中,某同学进行了一次投篮,篮球准确落入篮框内,建立如图所示的平面直角坐标系,篮球的运行轨迹可看作抛物线的一部分,则篮球在空中运行的最大高度为 .
14.某同学参加航模设计制作比赛,其设计的火箭升空高度(单位:)与飞行时间(单位:s)满足关系,当火箭升空到最高点时,距离地面 .
15.如图,某小区的景观池中安装一雕塑,米,喷出两股水流,两股水流可以抽象为平面直角坐标系中的两条抛物线(图中的,)的部分图象,两条抛物线的形状相同且顶点的纵坐标相同,且经测算发现抛物线的最高点(顶点)距离水池面米,且与的水平距离为米.小明同学打算操控微型无人机在,之间飞行,为了无人机的安全,要求无人机在竖直方向上的活动范围不小于米,设无人机与的水平距离为,则的取值范围是 .
16.如图所示,抛物线形拱桥的顶点距水面时,测得拱桥内水面宽为.当水面升高后,拱桥内水面的宽度减少 m.
三、解答题
17.某商场购进一批进货价为元的日用品,销售一段时间后,为了获得更多的利润,商店决定提高价格.调查发现,若按每件元的价格销售,每月能卖出件,若按每件元的价格销售,每月能卖件,假定每月销售量(件)是销售价格(元/件)的一次函数.
(1)求与之间的关系式;
(2)销售价定为多少元时,该商场每月获得利润最大?最大利润是多少?
18.某小区花园新安装了一排音乐喷泉装置,其中位于中间的喷水装置喷水能力最强,水流在各个方向上沿形状相同的抛物线路径落下,若喷出的水流高度为,水流与之间的水平距离为,y与x之间满足二次函数关系.如图所示,经测量,喷水装置高度为3.5米,水流最高处离喷水装置的水平距离为3米,离地面竖直距离为8米.
(1)求水流喷出的高度与水平距离之间的函数关系式;
(2)若在音乐喷泉四周摆放花盆,不计其它因素,花盆需至少离喷水装置多少米处,才不会被喷出的水流击中?
19.如图,在矩形中,,,点是的中点.动点从点出发,沿折线以的速度运动,作,交边或边于点,连接.当点与点重合时,点停止运动.设点的运动时间为,的面积为.
(1)当时,的形状是______.
(2)当点Q与点B重合时,求x的值.
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
20.如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同,正常水位时,大孔水面宽度米,顶点距水面米(即米),小孔顶点距水面米(即米),当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度.
21.在文艺汇演来临之际,九年级2班同学准备装饰教室.他们在相对的两面墙上的B,C两点之间拉了一根彩带,彩带自然下垂后呈抛物线形,地面上两点O,D分别在点B,C的正下方,已知米,和之间的水平距离为10米.以所在直线为y轴,所在直线为x轴建立如图1所示的平面直角坐标系,此时彩带自然下垂形状可近似看作抛物线.
(1)求该抛物线的函数表达式及彩带到地面的最小距离.
(2)为了使彩带的造型美观,现将图1中彩带最低点固定在灯E上(灯宽度、厚度不计,图中所有点均在同一竖直平面内),且灯E到和的距离相等,这样灯E两侧的彩带就形成了两个对称的新抛物线,如图2所示.若两个新抛物线最低点之间的水平距离为4米,且灯E到地面的距离为2.7米,则图2中彩带最低点比之前升高了多少米?
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C B A C B B C D
1.C
【分析】本题考查了二次函数在实际问题中的应用.将函数解析式写成顶点式,然后根据二次函数的性质可得答案.
【详解】解:
,
∵,
∴当时,s取最大值,且最大值是600.
即飞机滑行才能停下来.
故选:C.
2.B
【分析】本题考查二次函数的实际应用,掌握二次函数的性质,是解题的关键.令,求出的值即可.
【详解】解:∵,
∴当时,即:,
解得:或,
∴球弹起后又回到地面所经过的时间是3秒.
故选:B.
3.A
【分析】本题考查了根据实际问题列二次函数关系式,由铁栅栏的全长及的长,可得出平行于墙的一边长为米,再利用长方形的面积公式,即可找出y关于x的函数关系式.
【详解】解:铁栅栏的全长为15米,米,
平行于墙的一边长为米.
根据题意得:.
故选:A
4.C
【分析】本题考查了二次函数的应用.根据二次函数的图象与性质,分析即可得到答案.
【详解】解:由题意得,解得,①结论正确;
函数关系,
∵,
∴小球的飞行高度最高可达到,②结论错误;
解方程,
得或,
∴小球有两个飞行的时间使小球的高度刚好达到,③结论正确.
故选:C.
5.B
【分析】本题考查了二次函数在实际问题中的应用,数形结合并熟练掌握二次函数的性质是解题的关键.设垂直于墙的一边为,则隔离区的另一边为,根据矩形的面积公式列出面积关于的函数解析式,再根据题意求出的取值范围,然后分别令和,解方程求出,取在取值范围内的值即可.
【详解】解:设垂直于墙的一边为,则隔离区的另一边为,
;
根据题意,得不等式组,
解得:,
当时,,
解得(不合题意,舍去);
当时,,
解得,(不合题意,舍去),
故小亮说法正确.
故选:B.
6.B
【分析】本题考查二次函数的应用.根据生产成本和销售价格均是生产数量的一次函数以及表格中的数据,得到生产成本和销售价格的表达式,进而根据利润每件产品的利润生产数量,把相关数值代入可生产利润得关于生产数量的二次函数,进而根据二次函数的性质可得生产数量为多少时,利润最大.
【详解】解:设生产数量为万件,生产成本为元件,销售价格为元件.
生产成本和销售价格均是生产数量的一次函数,
设,.
,符合,
,
解得:.
.
,符合,
.
解得:.
.
设生产利润为,则
.
,
当时,利润最大,
即为获最大利润,生产数量应为4万件.
故选:B.
7.C
【分析】本题考查了二次函数的应用,勾股定理,列函数关系是解题的关键.
先根据勾股定理求出的长,再设点 P 运动时间为t,四边形的面积为y,根据题意表示出y与t的函数关系式,进一步利用二次函数的性质即可求解.
【详解】解:由题可知,是直角三角形,
∴,
设点 P 运动时间为t,四边形的面积为y,
则,
∴,
则当时,y最小为.
故选:C.
8.D
【分析】本题考查了二次函数的应用,要使其落入锅中,需要满足,由即可求解;找出的取值范围是解题的关键.
【详解】解:由题意得
,
解得:,(舍去),
要使其落入锅中,
,
,
,
,
,
不可能;
故选:D.
9.121
【分析】本题主要考查了图形和二次函数的问题,根据二次函数的性质解题即可.
【详解】解:由函数关系可知,
∵二次函数的二次项系数即,
∴当时,y最大值.
故答案为:121.
10.不会
【分析】本题考查二次函数的实际应用,将代入函数解析式,求出刹车距离,进行判断即可.
【详解】解:∵,
∴当时,,
∵,
∴此时刹车不会撞上前面的故障车;
故答案为:不会.
11.
【分析】本题主要考查二次函数的应用,找准等量关系是解题的关键.根据题意列出二次函数,利用二次函数的性质解题即可.
【详解】解:设房价定为元,每天的利润为元,
,
,
,
因为,
故当时,获得最大利润.
故答案为:.
12.9
【分析】本题主要考查了二次函数的应用.依据题意,令,得到关于的方程,解方程即可得出结论.
【详解】解:令,则,
解得:或(不合题意,舍去),
,
.
故答案为:9.
13.3.6//
【分析】本题主要考查了二次函数的应用,熟练掌握二次函数的图像与性质是解题关键.将抛物线解析式转化为顶点式,即可获得答案.
【详解】解:∵,
∴当时,取最大值,最大值为,
即篮球在空中运行的最大高度为.
故答案为:3.6.
14.54
【分析】本题考查了二次函数的应用,直接利用配方法将化为顶点式,进而求解即可,熟练掌握配方法是解题的关键.
【详解】由题意得,
∵,
∴抛物线开口向下,
∴当时,h取最大值,
∴当火箭升空到最高点时,距离地面,
故答案为:54.
15.
【分析】本题考查二次函数的应用,根据题意正确求出函数的解析式是解题关键.
先由题意可知抛物线过点,顶点为点,用待定系数法可求得解析式;再根据两条抛物线的形状相同且顶点的纵坐标相同且经过点,设的解析式为,代入相关数据即可求得解析式,再根据题意进行取舍即可;设无人机的横坐标为,根据题意列出不等式:和,求解即可.
【详解】解:由已知可得:抛物线过点,,
设其解析式为,
把代入得:,
解得,
,
抛物线的解析式为:,
令时,,,
∴,
由两条抛物线的形状相同,设的解析式为,
已知经过点,
∴的解析式为,
两条抛物线顶点的纵坐标相同,
,
解得,
的解析式为①或②,
当时,
①,解得,,;
②,解得,,;
由图可知的顶点的横坐标小于,故舍去①,
的解析式为,
∴,
由题意可得:,
解得:,
又,
解得:,
,
故答案为:.
16.
【分析】本题考查扫物线的性质及应用,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,是中档题.
建立平面直角直角坐标系,设抛物线方程为,由题意知抛物线的顶点坐标是,且抛物线经过点,求出抛物线方程为.由此能求出结果.
【详解】建立如图所示的平面直角坐标系,
设抛物线为,
由题意知抛物线的顶点坐标是,且抛物线经过点,
解得:
∴抛物线方程为.
当水面升高后,,则,解得.
∴当水面升高后,拱桥内水面宽度是米.
当水面升高后,拱桥内水面的宽度减少m.
故答案为:.
17.(1);
(2)销售价定为元时,该商场每月获得利润最大,最大利润是元.
【分析】本题考查二次函数的应用能力,理解题意找到题目的等量关系列出函数关系式是解题的关键;
(1)根据题意利用待定系数法求函数解析式;
(2)根据月利润单件利润月销量列出函数解析式,根据函数的性质求最值即可;
【详解】(1)解:(1)设与之间的关系式为,
根据题意得:,
解得:,
则与之间的函数关系式为;
(2)设利润元,则与的函数关系式是:
,
,
当时,有最大值,最大值为,
销售价定为元时,该商场每月获得利润最大,最大利润是元;
18.(1)
(2)7米
【分析】本题考查二次函数的顶点式,以及二次函数的应用,理解题意是关键.
(1)依据题意得,抛物线的顶点为,从而可设抛物线为,又抛物线过,进而计算可以得解;
(2)依据题意,由抛物线为,进而令,则,求出x的值即可判断得解.
【详解】(1)由题意得,抛物线的顶点为,
∴可设抛物线为.
又抛物线过,
∴.
∴.
∴水流喷出的高度与水平距离之间的函数关系式为.
(2)由题意,∵抛物线为,
∴令,则.
∴或(不合题意,舍去).
∴花盆需至少离喷水装置为7米处,才不会被喷出的水流击中.
19.(1)等腰直角三角形
(2)3
(3)当时,;当时,;当时,
【分析】(1)由题意得出当时,点在上,如图,作于,则,证明,得出,即可得证;
(2)求出当点与点重合时,此时点的运动的距离为,计算即可得出答案;
(3)分三个阶段:当时,点在上运动;当时,点在上运动,作于;当时,点在上运动,作于,分别利用矩形的判定与性质、三角形全等的判定与性质、勾股定理、三角形面积公式计算即可得出答案.
【详解】(1)解:当时,点运动的距离为:,
∵四边形是矩形,
∴,,,
∵点是的中点.
∴,
∴当时,点在中点上,
如图,作于,则,
∴四边形为矩形,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴的形状是等腰直角三角形;
(2)如图,当点与点重合时,
∵,
∴四边形是矩形,
∴,
∴,
∴此时点的运动的距离为,
∴;
(3)∵四边形是矩形,
∴,,,
∵点是的中点.
∴,
如图,当时,点在上运动,
,
此时,
∵,
∴四边形是矩形,
∴,
∴;
如图,当时,点在上运动,作于,则,
∴四边形为矩形,
∴,
同(1)可得,,
∴,
∴的形状是等腰直角三角形,
由题意得:,
∴,
∴,
∴;
如图,当时,点在上运动,作于,
同理可得:四边形为矩形,,
∴,,,
∵,
∴,
∴,
∴,
∴,
∴,
综上所述,.
【点睛】本题考查了矩形的判定与性质、三角形全等的判定与性质、勾股定理、等腰直角三角形的判定与性质,二次函数的应用等知识点,熟练掌握以上知识点并灵活运用,添加适当的辅助线,采用分类讨论的思想是解此题的关键.
20.米
【分析】此题主要考查的是待定系数法求解析式以及二次函数的对称性,求出二次函数的解析式是解决问题的关键;
设出大孔抛物线的解析式的一般形式,代入点的坐标求得函数解析式,再由点的纵坐标代入即可解答.
【详解】解:设大孔对应的抛物线解析式为:,依题意得,,
,
解得:,
即,
当时,,
解得:,
,,
即此时大孔的水面宽度为米
21.(1)抛物线的函数表达式为,彩带到地面的最小距离为2.25米
(2)图2中彩带最低点比之前升高了0.21米
【分析】本题主要考查了二次函数的应用,解题时要熟练掌握并能灵活运用二次函数的性质解题是关键.
(1)依据题意,可知抛物线的对称轴为直线,且过点,,进而可得,故可得,从而可得函数的解析式,当时,,进而可以判断得解;
(2)依据题意,由两个新抛物线对称,且最低点之间的水平距离为4米,可得左边的新抛物线的对称轴为直线,再设左边的新抛物线的函数表达式为,又,,进而求出解析式后即可判断得解.
【详解】(1)由题意,可知抛物线的对称轴为直线,且过点,且,
∴,
∴.
∴抛物线的函数表达式为.
当时,,
∴彩带到地面的最小距离为2.25米.
(2)∵两个新抛物线对称,且最低点之间的水平距离为4米,
∴左边的新抛物线的对称轴为直线.
设左边的新抛物线的函数表达式为.
由题意,可知,.
把,代入中,
得
解得
(米).
答:图2中彩带最低点比之前升高了0.21米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
