北师大版六年级上册数学2.7 练习二 课件(共35张PPT)
文档属性
| 名称 | 北师大版六年级上册数学2.7 练习二 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
第7课时 练习二
第二单元 分数混合运算
这一个单元我们都学了什么呢?
运算顺序
运算律
解决实际问题
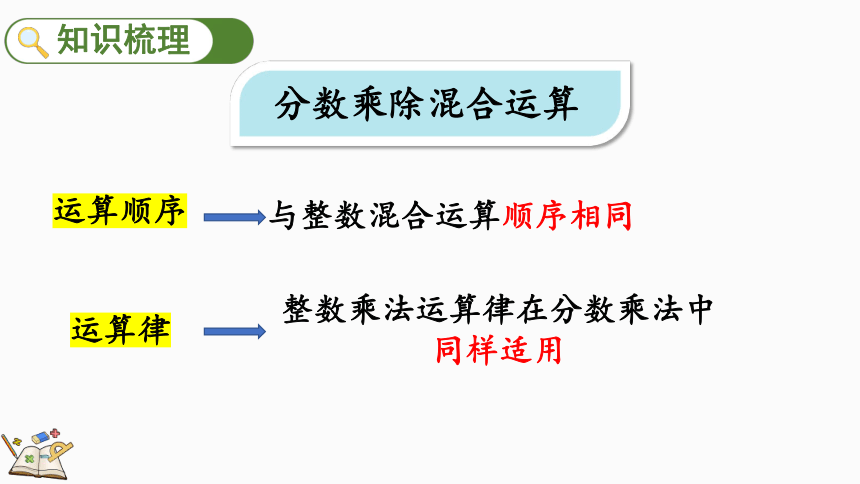
运算律
整数乘法运算律在分数乘法中同样适用
运算顺序
与整数混合运算顺序相同
分数乘除混合运算
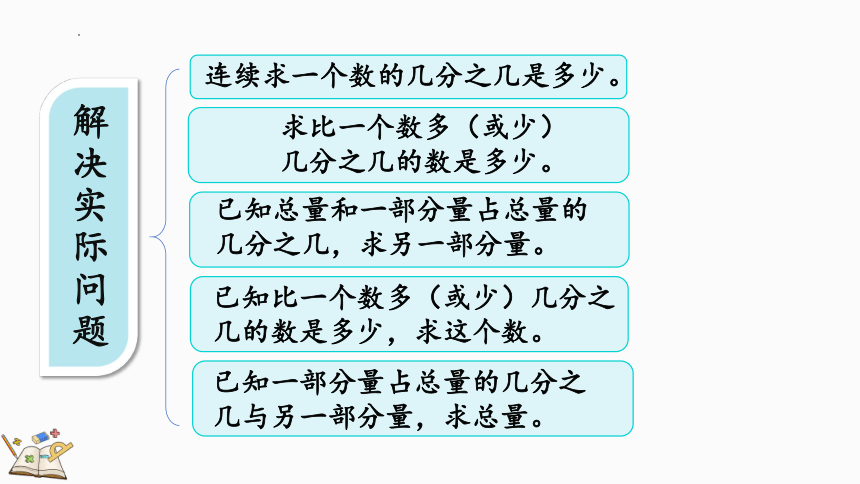
已知一部分量占总量的几分之几与另一部分量,求总量。
已知比一个数多(或少)几分之几的数是多少,求这个数。
已知总量和一部分量占总量的几分之几,求另一部分量。
解决实际问题
连续求一个数的几分之几是多少。
求比一个数多(或少)几分之几的数是多少。
分数乘除混合运算的计算方法
1.分数乘除混合运算与整数的运算顺序相同。
2.计算时先要把分数连除或分数乘除混合运
算转换成连乘运算,然后约分再计算。
整数的运算律在分数运算中的应用
整数运算律和性质对分数四则混合运算同样适用。
分数连乘应用题
连续求一个数的几分之几是多少,可以用分数连乘来解决。
分数连乘运算,可以一次计算,能约分的要先约分。
方法一:
单位“1 ”的量±单位“1 ”的量×另一个量比单位“ 1 ”的量多(少)的几分之几=另一个量(乘加或乘减)
求比一个数多(或少)几分之几的数是多少问题
方法二:
单位“1 ”的量×(1±另一个量比单位“1 ”的量多/少的几分之几)=另一个量。 (乘加或乘减)
已知总量和一部分量占总量的几分之几,求另一部分量
方法一:
总量-总量×一部分量占总量的几分之几=另一部分量。
方法二:
总量×(1-一部分量占总量的几分之几)=另一部分量。
单位“1”未知,用方程解答问题
2.已知一部分量占总量的几分之几与另一部分量,求总量。
1.已知比一个数多(或少)几分之几的数是多少,求这个数。
用方程解分数混合运算的实际问题,根据分数乘法的意义,顺向思考,先找到等量关系,列方程解答。
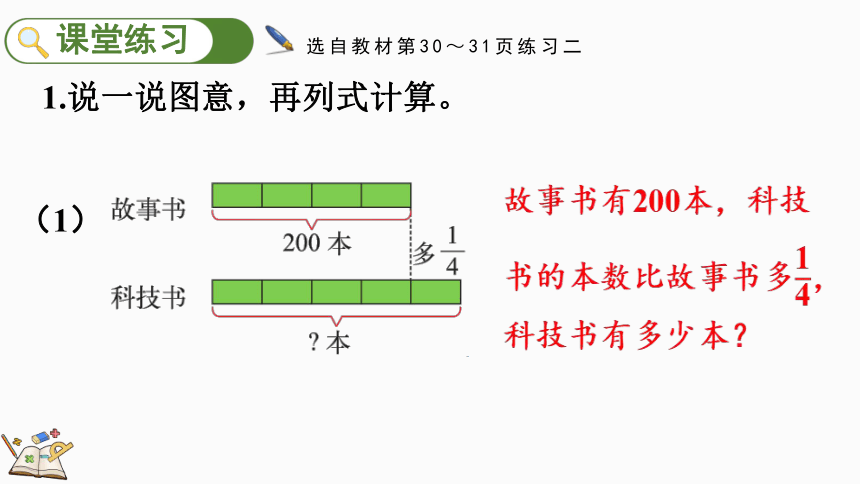
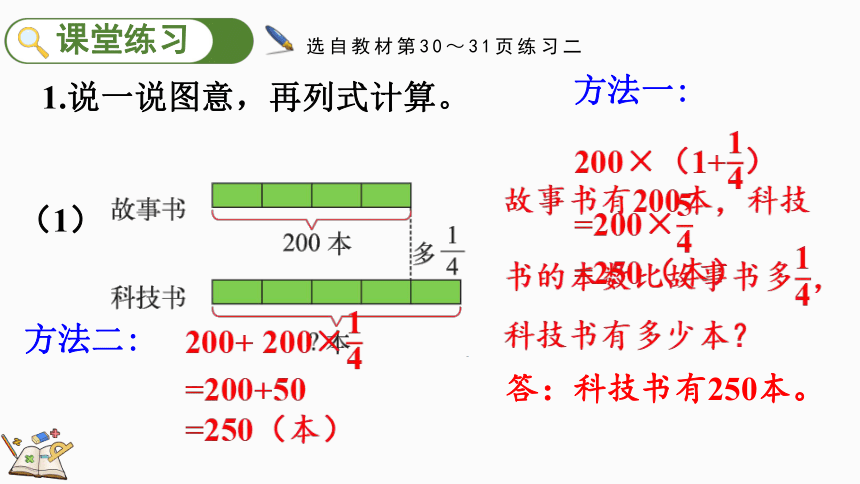
1.说一说图意,再列式计算。
故事书有200本,科技书的本数比故事书多,科技书有多少本?
(1)
选自教材第30~31页练习二
1.说一说图意,再列式计算。
故事书有200本,科技书的本数比故事书多,科技书有多少本?
(1)
200×(1+)
=200×
=250(本)
方法一:
200+ 200×
=200+50
=250(本)
方法二:
答:科技书有250本。
选自教材第30~31页练习二
(2)
钢笔有25支,比中性笔多中性笔有多少支?
1.说一说图意,再列式计算。
选自教材第30~31页练习二
解:设中性笔有支。
方法一:
(2)
钢笔有25支,比中性笔多中性笔有多少支?
1.说一说图意,再列式计算。
解:设中性笔有支。
方法二:
答:中性笔有20支。
选自教材第30~31页练习二
=20
方法三:
答:中性笔有20支。
选自教材第30~31页练习二
(2)
钢笔有25支,比中性笔多中性笔有多少支?
1.说一说图意,再列式计算。
2.某仓库的地面是长方形的,长15m,宽是长的。
这个仓库地面的面积是多少?
15×
=12×15
=180(平方米)
答:这个仓库地面的面积是180平方米。
长方形面积=长×宽
3.六(2)班有45名学生,其中的学生参加校运会的各项
比赛,其余的学生组成啦啦队。共有多少名啦啦队员?
=18(名)
答:共有18名啦啦队员。
4.
× ×
= ×
=
×
=
=
(1+)×10
=1××10
=10+
=10
4÷
=4×
=
=
98÷(÷)
= 98÷(×)
= 98÷
= 98×
= 420
4.
36×36×
=36×()
=36×1
=36
x+x=13
4.5x+x
x=13
x=
5.5x=
x=
5.解方程。
解:
解:
x=
x=
x=
解:
6.世界人均水资源拥有量是8400m ,而我国人均水资源
拥有量只有世界人均水资源拥有量的,我国人均水
资源拥有量比世界人均水资源拥有量少多少立方米?
8
=6300(立方米)
答:我国人均水资源拥有量比世界人均水资源拥有量少6300立方米。
我比小华重
我的体重是35千克
我比小华轻
小刚
小华
小明
(1)画图表示三人体重之间的关系。
7.
小华
小刚
比小华重
?千克
35千克
?千克
小明
比小华轻
(1)画图表示三人体重之间的关系。
7.
小刚: 35×(1+)
答:小刚的体重是42千克,小明的体重是30千克。
小明: 35×(1-)
=35×
=42(千克)
=35×
=30(千克)
(2)小刚和小明的体重分别是多少千克?算一算。
7.
8.(1)一份稿件共4500字,淘气录入了这份稿件的,
还剩多少字没录入?
答:还剩下2500字没录入。
4500×(1)
=4500×
=2500(字)
解:设这份稿件共有x字。
答:这份稿件共有2450字。
(1- x =700
=700
=700÷
=2450
8.(2)笑笑录入一份稿件,录入了后还剩700字,
这份稿件共有多少字?
9.
《算法统宗》中,许多数学问题都是以歌诀形式呈现的,其中有一首“以碗知僧”。
以碗知僧
巍巍古寺在山中,不知寺内几多僧。三百六十四只碗,恰合用尽不差争。三人共食一碗饭,四人共尝一碗羹。请问先生能算者,都来寺内几多僧。
——摘自(明)程大位著《算法统宗》
9.
大意是:山上有一古寺叫都来寺,在这座寺庙里,3个和尚合吃一碗饭,4个和尚合分一碗汤,一共用了364只碗。请问都来寺里有多少个和尚。
以碗知僧
巍巍古寺在山中,不知寺内几多僧。三百六十四只碗,恰合用尽不差争。三人共食一碗饭,四人共尝一碗羹。请问先生能算者,都来寺内几多僧。
——摘自(明)程大位著《算法统宗》
利用方程知识可以解决这个有趣的问题,我们试一下吧!
解:设都来寺里有x个和尚。
x+x=364
x=364
x=364÷
x=624
答:都来寺里有624个和尚。
9.
某车间有男工人24名,比女工人多。这个车间有女工人多少名?
解:设这个车间有女工人x名。
14
答:这个车间有女工人14名。
方法一:
方法二:
解:设这个车间有女工人x名。
某车间有男工人24名,比女工人多。这个车间有女工人多少名?
方法三:
答:这个车间有女工人14名。
黑熊皮皮买来一桶蜂蜜,第一天吃掉 ,第二天吃掉10kg,还剩一半。这桶蜂蜜原来有多少千克?
=
=10
=100
方法一:
答:这桶蜂蜜原来有100千克。
解:设这桶蜂蜜原来有x千克。
就是
原来的质量-(第一天吃掉的质量+还剩下的质量)=第二天吃掉的质量。
10÷(
=10÷
=100(千克)
方法二:
答:这桶蜂蜜原来有100千克。
黑熊皮皮买来一桶蜂蜜,第一天吃掉 ,第二天吃掉10kg,还剩一半。这桶蜂蜜原来有多少千克?
就是
这节课有什么收获呢?
分数混合运算
分数乘除混合运算的计算方法
解决有关“增加几分之几“的问题
分数连乘应用题
整数的运算律在分数运算中的应用
用方程解决与分数混合运算有关的实际问题
单位“1”未知:用方程或除法解答。
练习二
单位“1”已知:用乘法解答。
运算律对于分数同样适用。
分数混合运算的顺序与整数相同
计算
解决问题
第7课时 练习二
第二单元 分数混合运算
这一个单元我们都学了什么呢?
运算顺序
运算律
解决实际问题
运算律
整数乘法运算律在分数乘法中同样适用
运算顺序
与整数混合运算顺序相同
分数乘除混合运算
已知一部分量占总量的几分之几与另一部分量,求总量。
已知比一个数多(或少)几分之几的数是多少,求这个数。
已知总量和一部分量占总量的几分之几,求另一部分量。
解决实际问题
连续求一个数的几分之几是多少。
求比一个数多(或少)几分之几的数是多少。
分数乘除混合运算的计算方法
1.分数乘除混合运算与整数的运算顺序相同。
2.计算时先要把分数连除或分数乘除混合运
算转换成连乘运算,然后约分再计算。
整数的运算律在分数运算中的应用
整数运算律和性质对分数四则混合运算同样适用。
分数连乘应用题
连续求一个数的几分之几是多少,可以用分数连乘来解决。
分数连乘运算,可以一次计算,能约分的要先约分。
方法一:
单位“1 ”的量±单位“1 ”的量×另一个量比单位“ 1 ”的量多(少)的几分之几=另一个量(乘加或乘减)
求比一个数多(或少)几分之几的数是多少问题
方法二:
单位“1 ”的量×(1±另一个量比单位“1 ”的量多/少的几分之几)=另一个量。 (乘加或乘减)
已知总量和一部分量占总量的几分之几,求另一部分量
方法一:
总量-总量×一部分量占总量的几分之几=另一部分量。
方法二:
总量×(1-一部分量占总量的几分之几)=另一部分量。
单位“1”未知,用方程解答问题
2.已知一部分量占总量的几分之几与另一部分量,求总量。
1.已知比一个数多(或少)几分之几的数是多少,求这个数。
用方程解分数混合运算的实际问题,根据分数乘法的意义,顺向思考,先找到等量关系,列方程解答。
1.说一说图意,再列式计算。
故事书有200本,科技书的本数比故事书多,科技书有多少本?
(1)
选自教材第30~31页练习二
1.说一说图意,再列式计算。
故事书有200本,科技书的本数比故事书多,科技书有多少本?
(1)
200×(1+)
=200×
=250(本)
方法一:
200+ 200×
=200+50
=250(本)
方法二:
答:科技书有250本。
选自教材第30~31页练习二
(2)
钢笔有25支,比中性笔多中性笔有多少支?
1.说一说图意,再列式计算。
选自教材第30~31页练习二
解:设中性笔有支。
方法一:
(2)
钢笔有25支,比中性笔多中性笔有多少支?
1.说一说图意,再列式计算。
解:设中性笔有支。
方法二:
答:中性笔有20支。
选自教材第30~31页练习二
=20
方法三:
答:中性笔有20支。
选自教材第30~31页练习二
(2)
钢笔有25支,比中性笔多中性笔有多少支?
1.说一说图意,再列式计算。
2.某仓库的地面是长方形的,长15m,宽是长的。
这个仓库地面的面积是多少?
15×
=12×15
=180(平方米)
答:这个仓库地面的面积是180平方米。
长方形面积=长×宽
3.六(2)班有45名学生,其中的学生参加校运会的各项
比赛,其余的学生组成啦啦队。共有多少名啦啦队员?
=18(名)
答:共有18名啦啦队员。
4.
× ×
= ×
=
×
=
=
(1+)×10
=1××10
=10+
=10
4÷
=4×
=
=
98÷(÷)
= 98÷(×)
= 98÷
= 98×
= 420
4.
36×36×
=36×()
=36×1
=36
x+x=13
4.5x+x
x=13
x=
5.5x=
x=
5.解方程。
解:
解:
x=
x=
x=
解:
6.世界人均水资源拥有量是8400m ,而我国人均水资源
拥有量只有世界人均水资源拥有量的,我国人均水
资源拥有量比世界人均水资源拥有量少多少立方米?
8
=6300(立方米)
答:我国人均水资源拥有量比世界人均水资源拥有量少6300立方米。
我比小华重
我的体重是35千克
我比小华轻
小刚
小华
小明
(1)画图表示三人体重之间的关系。
7.
小华
小刚
比小华重
?千克
35千克
?千克
小明
比小华轻
(1)画图表示三人体重之间的关系。
7.
小刚: 35×(1+)
答:小刚的体重是42千克,小明的体重是30千克。
小明: 35×(1-)
=35×
=42(千克)
=35×
=30(千克)
(2)小刚和小明的体重分别是多少千克?算一算。
7.
8.(1)一份稿件共4500字,淘气录入了这份稿件的,
还剩多少字没录入?
答:还剩下2500字没录入。
4500×(1)
=4500×
=2500(字)
解:设这份稿件共有x字。
答:这份稿件共有2450字。
(1- x =700
=700
=700÷
=2450
8.(2)笑笑录入一份稿件,录入了后还剩700字,
这份稿件共有多少字?
9.
《算法统宗》中,许多数学问题都是以歌诀形式呈现的,其中有一首“以碗知僧”。
以碗知僧
巍巍古寺在山中,不知寺内几多僧。三百六十四只碗,恰合用尽不差争。三人共食一碗饭,四人共尝一碗羹。请问先生能算者,都来寺内几多僧。
——摘自(明)程大位著《算法统宗》
9.
大意是:山上有一古寺叫都来寺,在这座寺庙里,3个和尚合吃一碗饭,4个和尚合分一碗汤,一共用了364只碗。请问都来寺里有多少个和尚。
以碗知僧
巍巍古寺在山中,不知寺内几多僧。三百六十四只碗,恰合用尽不差争。三人共食一碗饭,四人共尝一碗羹。请问先生能算者,都来寺内几多僧。
——摘自(明)程大位著《算法统宗》
利用方程知识可以解决这个有趣的问题,我们试一下吧!
解:设都来寺里有x个和尚。
x+x=364
x=364
x=364÷
x=624
答:都来寺里有624个和尚。
9.
某车间有男工人24名,比女工人多。这个车间有女工人多少名?
解:设这个车间有女工人x名。
14
答:这个车间有女工人14名。
方法一:
方法二:
解:设这个车间有女工人x名。
某车间有男工人24名,比女工人多。这个车间有女工人多少名?
方法三:
答:这个车间有女工人14名。
黑熊皮皮买来一桶蜂蜜,第一天吃掉 ,第二天吃掉10kg,还剩一半。这桶蜂蜜原来有多少千克?
=
=10
=100
方法一:
答:这桶蜂蜜原来有100千克。
解:设这桶蜂蜜原来有x千克。
就是
原来的质量-(第一天吃掉的质量+还剩下的质量)=第二天吃掉的质量。
10÷(
=10÷
=100(千克)
方法二:
答:这桶蜂蜜原来有100千克。
黑熊皮皮买来一桶蜂蜜,第一天吃掉 ,第二天吃掉10kg,还剩一半。这桶蜂蜜原来有多少千克?
就是
这节课有什么收获呢?
分数混合运算
分数乘除混合运算的计算方法
解决有关“增加几分之几“的问题
分数连乘应用题
整数的运算律在分数运算中的应用
用方程解决与分数混合运算有关的实际问题
单位“1”未知:用方程或除法解答。
练习二
单位“1”已知:用乘法解答。
运算律对于分数同样适用。
分数混合运算的顺序与整数相同
计算
解决问题
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
