专项 集合创新题 课件(共20张PPT) 2024-2025学年数学-必修第一册-人教A版
文档属性
| 名称 | 专项 集合创新题 课件(共20张PPT) 2024-2025学年数学-必修第一册-人教A版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第一章 集合与常用逻辑用语
专项 集合创新题
数学-必修第一册-人教A版
题型一 新定义运算
1.(2023山东省实验中学期中)设集合,,,集合 ,定义
,,则 子集的个数是( )
B
A. B. C. D.10
【解析】 因为,0,,,所以,0,1,2,, ,又
, ,
则有2种情况,有5种情况,则的元素个数有个,所以 子集的个数是
.
2.(2024上海市行知中学期末)定义集合运算,且为集合 与集
合的差集;定义集合运算为集合与集合 的对称差.有以下4
个等式,, ,
,则4个等式中恒成立的是( )
B
A.①② B.①②③ C.①②④ D.①②③④
【解析】 由对称差的定义,知
,①正确;
由差集的定义,知 ,且
,且 ,
同理,则 ,
所以 ,表示的集合为图(1)中阴影部分所示,
同理 ,表示的集合也为图(1)中阴影部分所示,
所以 ,②正确;
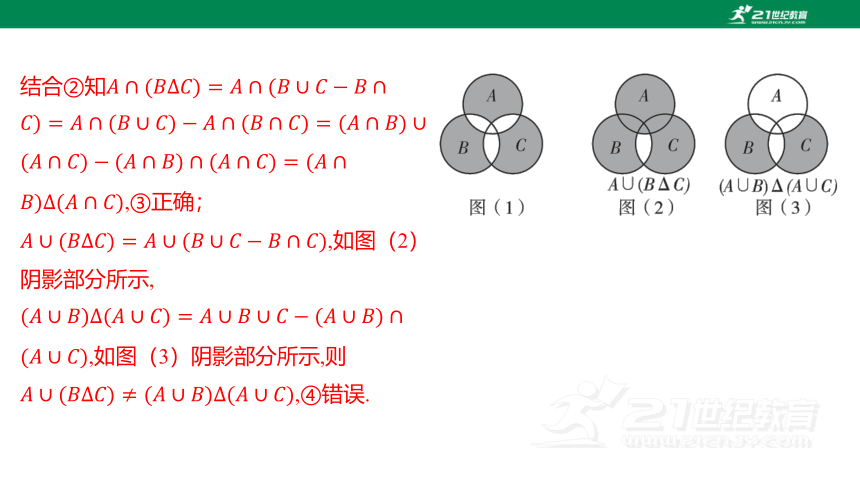
结合②知 ,③正确;
,如图(2)阴影部分所示,
,如图(3)阴影部分所示,则
,④错误.
3.(2024上海复旦大学附属中学期中)设为全集,对集合, ,定义运算“*”,满足
.若集合,,, ,
则 __________.
【解析】 由于,,,,则 ,所
以,则 ,
因此 .
题型二 新定义关系
4.(2024陕西榆林期中)若一个集合是另一个集合的子集,则称两个集合构成“鲸吞”,
若两个集合有公共元素,且互不为对方的子集,则称两个集合构成“蚕食”.对于集合
,,,,若这两个集合构成“鲸吞”或“蚕食”,则 的取值集
合为( )
C
A.,} B. C.,, D.{,
【解析】 分, 两种情况讨论.
当时, ,此时 ,即两个集合构成“鲸吞”;
当时,, },此时两个集合不能构成“鲸吞”,则两个集合构成“蚕食”,所以
或,解得或 ,
当时,,,两个集合构成“蚕食”,当时,, ,两个集合构成“蚕食”.
综上可得,的取值集合为,, .
5.(2023山东德州一中月考)设是整数集的一个非空子集,若存在 ,满足
或,则称是含“姊妹元素”的集合.对于给定的集合 ,
由的3个元素构成的所有子集中,含“姊妹元素”的集合 共有____ 个.
16
【解析】 由中的3个元素构成的子集有,,,,, ,
,,,,,,,,,,, ,
, ,共20个,
其中不含“姊妹元素”的集合有,,, ,共4个,所以含“姊妹元素”的
集合共有 个.
6.(2023广东梅州期末)是正整数集的非空子集,称集合, ,且
为集合的生成集.当时,集合的生成集_______;若 是由5个正
整数构成的集合,则其生成集 中元素个数的最小值为 ___ .
4
【解析】 若,则,,,所以 .
若是由5个正整数构成的集合,不妨设中元素为 ,且
,
可得,则 中至少有4个元素.
例如,则 ,
,,,此时 ,有4
个元素,所以生成集 中元素个数的最小值为4.
题型三 新定义概念
7.(2024山西省际名校联考)设是一个数集,且至少含有两个数,若对任意的, ,
都有,,,(除数),则称 是一个数域,则下列集合为数域的是
( )
C
A. B. C. D., }
【解析】 1,,但,故 不是数域,A错误,同理B错误;
任意的,,都有,,,,故 是一个数域,C正确;
对于集合,,,但,故, }不是数域,D错误.
8.(2024广东佛山一中月考,多选)给定数集,若对于任意, ,都有
,且,则称集合 为闭集合,则下列说法正确的是( )
BC
A.集合,,0,2, 为闭集合
B.整数集是闭集合
C.集合, }为闭集合
D.若集合,为闭集合,则 也为闭集合
【解析】 ,,,但 ;
整数加减整数的结果为整数;
的倍数的整数加减结果为3的倍数的整数;
如,,,},其中, ,
.
9.(2024浙江杭州期中)定义1:通常我们把一个以集合作为元素的集合称为族.
定义2:集合的一个拓扑是以的子集为元素的一个族.它满足以下条件:和 都
在中;的任意子集的并集在中;的任意有限子集的交集在 中.
(1)族,,族,判断族与族是否为集合 的拓扑;
【解】经检验,族和族满足定义2中的三个条件,则族,,
都是集合 的拓扑.
(2)设有限集 为全集,
(ⅰ)证明 ;
【证明】 设,则 ,
故存在整数使,因此,得 .
设,则存在整数使,故 ,
因此 ,
得 ,即证.
(ⅱ)族 为集合的一个拓扑,证明:由族 所有元素的补集构成的族为集合 的
一个拓扑.
因为,,,,所以, ,符合条件①;
设,, ,为的任意子集,则,, ,,
由知 ,
因为,所以 ,符合条件③;
,
因为,所以 ,符合条件②.即证.
题型四 新定义性质
10.(2024上海市位育中学期中)设全集 ,对其子集引进“势”的概念:①
空集的“势”最小;②非空子集中的元素越多,其“势”越大;③若两个子集中的元素个数
相同,则子集中最大的元素越大,子集的“势”就越大,若最大的元素相同,则第二大的
元素越大,子集的“势”就越大,依次类推.若将全集 全部的子集按“势”从小到大的顺序
排列,则排在第12位的子集是______ .
【解析】 元素个数为0的集合有1个, ;
元素个数为1的集合有5个,,,,, ;
元素个数为2的集合有10个,,,,,,,,,, .所以排
在第12位的子集是 .
11.(2024北京四中期中)若非空数集满足,,都有,则称集合 为无和集.
(1)判断集合, 是否为无和集,直接写出结论;
【解】集合是无和集,集合 不是无和集.
(2)给定正整数,集合,满足,2,,,且 ,求证:集
合, 不可能都是无和集;
假设,都是无和集,且,2,,, .
因为,所以1和2不能属于同一集合,不妨设,,又,所以 ,则
,,所以,则 ,
此时如果,则,则不是无和集,如果,则,则 不是无和集,与假
设矛盾,所以集合, 不可能都是无和集.
(3)给定正整数,集合,2, ,,且为无和集,求集合 中元素个数的
最大值(用含 的表达式表示).
当集合是由,2,3, , 中所有偶数组成的集合时,不符合无和集的定义,则可
设集合是由,2,3, ,中所有奇数组成的集合,易知集合是无和集.下面说明 是集
合 元素个数最多的情况.
假设加任意一个偶数到集合中,由于,因此1和 中有一个不属于
集合,即集合中的奇数至少减去一个,则元素个数不会比 中元素个数多.
故是偶数时,中元素个数的最大值为;是奇数时,中元素个数的最大值为 .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第一章 集合与常用逻辑用语
专项 集合创新题
数学-必修第一册-人教A版
题型一 新定义运算
1.(2023山东省实验中学期中)设集合,,,集合 ,定义
,,则 子集的个数是( )
B
A. B. C. D.10
【解析】 因为,0,,,所以,0,1,2,, ,又
, ,
则有2种情况,有5种情况,则的元素个数有个,所以 子集的个数是
.
2.(2024上海市行知中学期末)定义集合运算,且为集合 与集
合的差集;定义集合运算为集合与集合 的对称差.有以下4
个等式,, ,
,则4个等式中恒成立的是( )
B
A.①② B.①②③ C.①②④ D.①②③④
【解析】 由对称差的定义,知
,①正确;
由差集的定义,知 ,且
,且 ,
同理,则 ,
所以 ,表示的集合为图(1)中阴影部分所示,
同理 ,表示的集合也为图(1)中阴影部分所示,
所以 ,②正确;
结合②知 ,③正确;
,如图(2)阴影部分所示,
,如图(3)阴影部分所示,则
,④错误.
3.(2024上海复旦大学附属中学期中)设为全集,对集合, ,定义运算“*”,满足
.若集合,,, ,
则 __________.
【解析】 由于,,,,则 ,所
以,则 ,
因此 .
题型二 新定义关系
4.(2024陕西榆林期中)若一个集合是另一个集合的子集,则称两个集合构成“鲸吞”,
若两个集合有公共元素,且互不为对方的子集,则称两个集合构成“蚕食”.对于集合
,,,,若这两个集合构成“鲸吞”或“蚕食”,则 的取值集
合为( )
C
A.,} B. C.,, D.{,
【解析】 分, 两种情况讨论.
当时, ,此时 ,即两个集合构成“鲸吞”;
当时,, },此时两个集合不能构成“鲸吞”,则两个集合构成“蚕食”,所以
或,解得或 ,
当时,,,两个集合构成“蚕食”,当时,, ,两个集合构成“蚕食”.
综上可得,的取值集合为,, .
5.(2023山东德州一中月考)设是整数集的一个非空子集,若存在 ,满足
或,则称是含“姊妹元素”的集合.对于给定的集合 ,
由的3个元素构成的所有子集中,含“姊妹元素”的集合 共有____ 个.
16
【解析】 由中的3个元素构成的子集有,,,,, ,
,,,,,,,,,,, ,
, ,共20个,
其中不含“姊妹元素”的集合有,,, ,共4个,所以含“姊妹元素”的
集合共有 个.
6.(2023广东梅州期末)是正整数集的非空子集,称集合, ,且
为集合的生成集.当时,集合的生成集_______;若 是由5个正
整数构成的集合,则其生成集 中元素个数的最小值为 ___ .
4
【解析】 若,则,,,所以 .
若是由5个正整数构成的集合,不妨设中元素为 ,且
,
可得,则 中至少有4个元素.
例如,则 ,
,,,此时 ,有4
个元素,所以生成集 中元素个数的最小值为4.
题型三 新定义概念
7.(2024山西省际名校联考)设是一个数集,且至少含有两个数,若对任意的, ,
都有,,,(除数),则称 是一个数域,则下列集合为数域的是
( )
C
A. B. C. D., }
【解析】 1,,但,故 不是数域,A错误,同理B错误;
任意的,,都有,,,,故 是一个数域,C正确;
对于集合,,,但,故, }不是数域,D错误.
8.(2024广东佛山一中月考,多选)给定数集,若对于任意, ,都有
,且,则称集合 为闭集合,则下列说法正确的是( )
BC
A.集合,,0,2, 为闭集合
B.整数集是闭集合
C.集合, }为闭集合
D.若集合,为闭集合,则 也为闭集合
【解析】 ,,,但 ;
整数加减整数的结果为整数;
的倍数的整数加减结果为3的倍数的整数;
如,,,},其中, ,
.
9.(2024浙江杭州期中)定义1:通常我们把一个以集合作为元素的集合称为族.
定义2:集合的一个拓扑是以的子集为元素的一个族.它满足以下条件:和 都
在中;的任意子集的并集在中;的任意有限子集的交集在 中.
(1)族,,族,判断族与族是否为集合 的拓扑;
【解】经检验,族和族满足定义2中的三个条件,则族,,
都是集合 的拓扑.
(2)设有限集 为全集,
(ⅰ)证明 ;
【证明】 设,则 ,
故存在整数使,因此,得 .
设,则存在整数使,故 ,
因此 ,
得 ,即证.
(ⅱ)族 为集合的一个拓扑,证明:由族 所有元素的补集构成的族为集合 的
一个拓扑.
因为,,,,所以, ,符合条件①;
设,, ,为的任意子集,则,, ,,
由知 ,
因为,所以 ,符合条件③;
,
因为,所以 ,符合条件②.即证.
题型四 新定义性质
10.(2024上海市位育中学期中)设全集 ,对其子集引进“势”的概念:①
空集的“势”最小;②非空子集中的元素越多,其“势”越大;③若两个子集中的元素个数
相同,则子集中最大的元素越大,子集的“势”就越大,若最大的元素相同,则第二大的
元素越大,子集的“势”就越大,依次类推.若将全集 全部的子集按“势”从小到大的顺序
排列,则排在第12位的子集是______ .
【解析】 元素个数为0的集合有1个, ;
元素个数为1的集合有5个,,,,, ;
元素个数为2的集合有10个,,,,,,,,,, .所以排
在第12位的子集是 .
11.(2024北京四中期中)若非空数集满足,,都有,则称集合 为无和集.
(1)判断集合, 是否为无和集,直接写出结论;
【解】集合是无和集,集合 不是无和集.
(2)给定正整数,集合,满足,2,,,且 ,求证:集
合, 不可能都是无和集;
假设,都是无和集,且,2,,, .
因为,所以1和2不能属于同一集合,不妨设,,又,所以 ,则
,,所以,则 ,
此时如果,则,则不是无和集,如果,则,则 不是无和集,与假
设矛盾,所以集合, 不可能都是无和集.
(3)给定正整数,集合,2, ,,且为无和集,求集合 中元素个数的
最大值(用含 的表达式表示).
当集合是由,2,3, , 中所有偶数组成的集合时,不符合无和集的定义,则可
设集合是由,2,3, ,中所有奇数组成的集合,易知集合是无和集.下面说明 是集
合 元素个数最多的情况.
假设加任意一个偶数到集合中,由于,因此1和 中有一个不属于
集合,即集合中的奇数至少减去一个,则元素个数不会比 中元素个数多.
故是偶数时,中元素个数的最大值为;是奇数时,中元素个数的最大值为 .
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
