2024--2025学年苏科版八年级数学上册第2章 轴对称图形提升训练(含答案)
文档属性
| 名称 | 2024--2025学年苏科版八年级数学上册第2章 轴对称图形提升训练(含答案) | 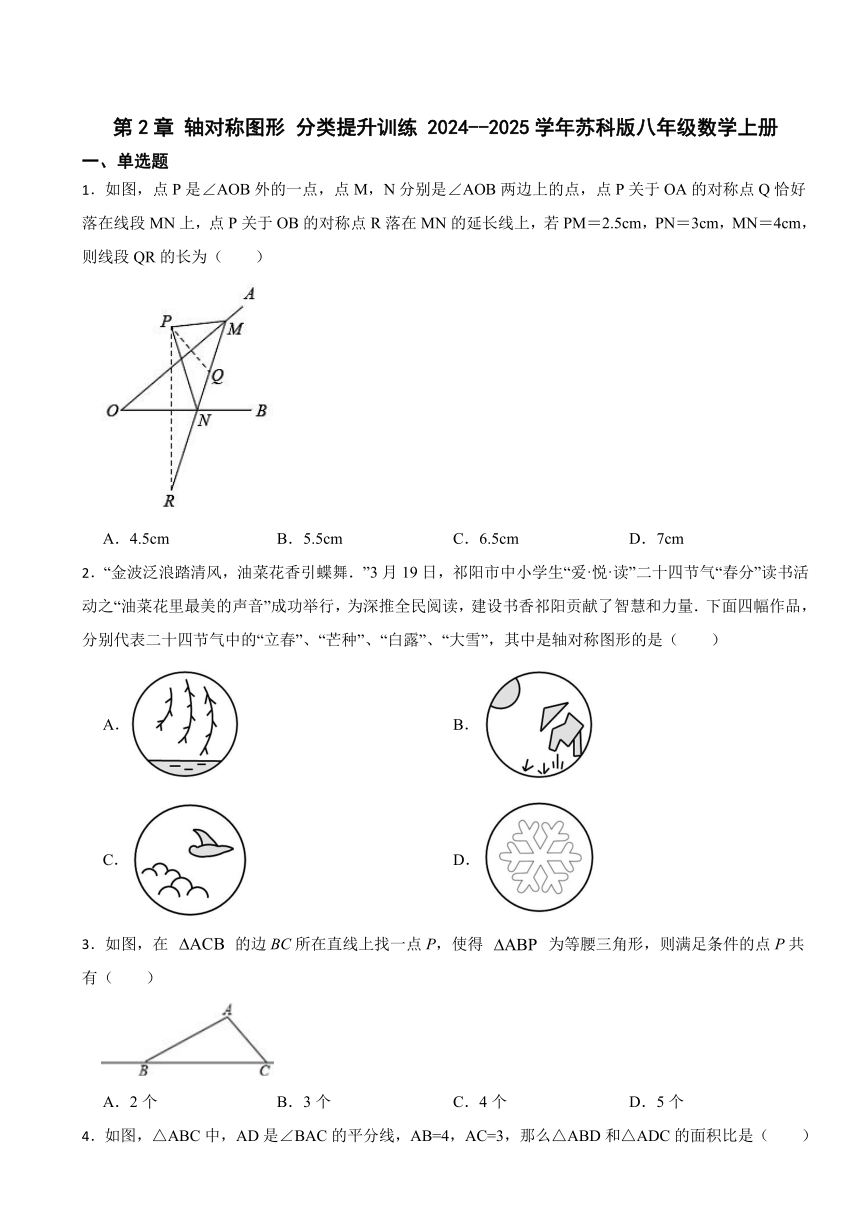 | |
| 格式 | docx | ||
| 文件大小 | 358.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 10:35:38 | ||
图片预览



文档简介
第2章 轴对称图形 分类提升训练 2024--2025学年苏科版八年级数学上册
一、单选题
1.如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上,若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为( )
A.4.5cm B.5.5cm C.6.5cm D.7cm
2.“金波泛浪踏清风,油菜花香引蝶舞.”3月19日,祁阳市中小学生“爱·悦·读”二十四节气“春分”读书活动之“油菜花里最美的声音”成功举行,为深推全民阅读,建设书香祁阳贡献了智慧和力量.下面四幅作品,分别代表二十四节气中的“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )
A. B.
C. D.
3.如图,在 的边BC所在直线上找一点P,使得 为等腰三角形,则满足条件的点P共有( )
A.2个 B.3个 C.4个 D.5个
4.如图,△ABC中,AD是∠BAC的平分线,AB=4,AC=3,那么△ABD和△ADC的面积比是( )
A.1:1 B.3:4 C.4:3 D.不能确定
5.如图,在等腰三角形中,,,点D为垂足,E、F分别是、上的动点.若,的面积为12,则的最小值是( )
A.2 B.4 C.6 D.8
6.已知是线段的垂直平分线,下列说法中正确的是( )
A.与距离相等的点在MN上
B.与点和点距离相等的点在上
C.与距离相等的点在上
D.垂直平分
7.如图,直线l1∥l2,将等边三角形如图放置若∠α=25°,则∠β等于( )
A.35° B.30° C.25° D.20°
8.如图,已知:,,平分,,有下列结论:①;②;③;④.结论正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,三角形纸片ABC中,∠A=80°,∠B=60°,将纸片的角折叠,使点C落在△ABC内,若∠α=30°,则∠β的度数是( )
A. B. C. D.
10.如图,中,是的角平分线,延长至,使得,连接.下列判断:;;平分;的面积的面积,一定成立的个数是( )
A.个 B.个 C.个 D.个
二、填空题
11.如图,①在OA、OB上分别截取线段OD、OE,使OD=OE;②分别以为圆心,大于的长为半径画弧,在内两弧交于点;③作射线.若∠AOB=60°,则 .
12.如图,已知 为等边三角形, 为中线,延长 至 ,使 连接 ,则 的长是 .
13.如图,在中,,点,分别在边,上,,则的度数为 .
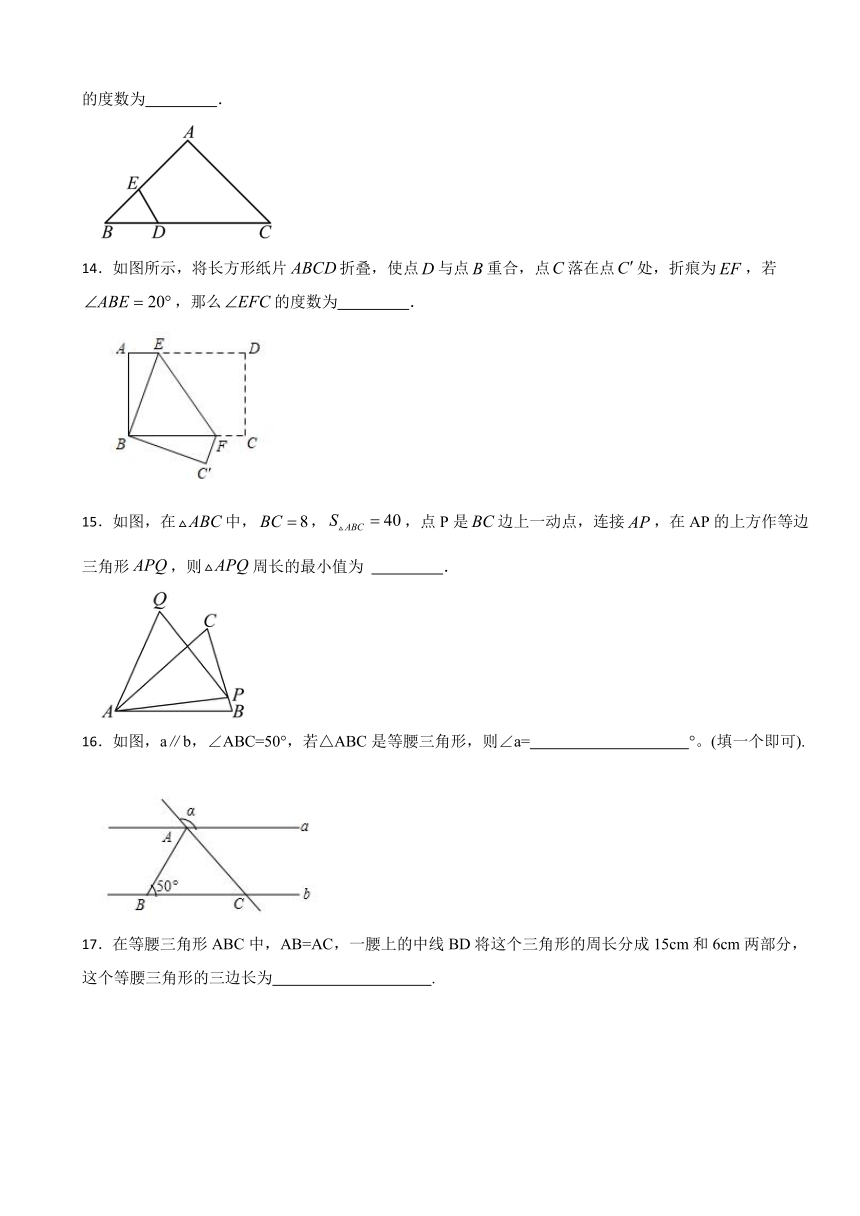
14.如图所示,将长方形纸片折叠,使点与点重合,点落在点处,折痕为,若,那么的度数为 .
15.如图,在中,,,点P是边上一动点,连接,在AP的上方作等边三角形,则周长的最小值为 .
16.如图,a∥b,∠ABC=50°,若△ABC是等腰三角形,则∠a= °。(填一个即可).
17.在等腰三角形ABC中,AB=AC,一腰上的中线BD将这个三角形的周长分成15cm和6cm两部分,这个等腰三角形的三边长为 .
三、解答题
18.已知点O为直线上一点,将直角三角板如图所示放置,且直角顶点在O处,在内部作射线,且恰好平分.
(1)若,求的度数;
(2)若,求的度数.
19.如图,直线,相交于点,,平分.若,求的度数.
20.如图,是的平分线,是的平分线.
(1)如果,,求的度数;
(2)如果,,求的度数;
21. 如图:在△ABC中,AB=AD=CD.
(1)若∠C=36°,求∠B的度数.
(2)若∠BAD=x°,∠C=y°, 求x和y的数量关系(用x的代数式表示y).
22.如图、直线、相交于点,于点,,平分,求的度数.
23.如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
答案解析部分
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】A
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】30
12.【答案】2
13.【答案】
14.【答案】125°
15.【答案】30
16.【答案】130(答案不唯一)
17.【答案】10cm,10cm,1cm
18.【答案】(1)
(2)
19.【答案】
20.【答案】(1)
(2)
21.【答案】(1)解:∵AD=CD
∴∠C=∠DAC=36°
∵∠ADB=∠C+∠DAC
∴∠ADB=36+36=72°
∵AB=AD
∴∠B=∠ADB =72°
(2)解:∵∠B+∠ADB+∠BAD=180°
∴∠B+∠ADB=(180-x)°
∵AB=AD
∴∠B=∠ADB =(90-x)°
∵AD=CD
∴∠C=∠DAC= y°
∵∠ADB=∠C+∠DAC
∴90-x=2y
∴y=45-x
22.【答案】
23.【答案】解:连接OA,OC,
∵OE,OF分别是AC,BD的垂直平分线,
∴OA=OC,OB=OD,
∵AB=CD,
∴△ABO≌△COD(SSS),
∴∠ABO=∠CDO,
设∠OBD=∠ODB=α,∠ABO=∠CDO=β,
∴α+β=120°,β﹣α=38°,
∴α=41°,
∴∠OBD=41°.
一、单选题
1.如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上,若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为( )
A.4.5cm B.5.5cm C.6.5cm D.7cm
2.“金波泛浪踏清风,油菜花香引蝶舞.”3月19日,祁阳市中小学生“爱·悦·读”二十四节气“春分”读书活动之“油菜花里最美的声音”成功举行,为深推全民阅读,建设书香祁阳贡献了智慧和力量.下面四幅作品,分别代表二十四节气中的“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )
A. B.
C. D.
3.如图,在 的边BC所在直线上找一点P,使得 为等腰三角形,则满足条件的点P共有( )
A.2个 B.3个 C.4个 D.5个
4.如图,△ABC中,AD是∠BAC的平分线,AB=4,AC=3,那么△ABD和△ADC的面积比是( )
A.1:1 B.3:4 C.4:3 D.不能确定
5.如图,在等腰三角形中,,,点D为垂足,E、F分别是、上的动点.若,的面积为12,则的最小值是( )
A.2 B.4 C.6 D.8
6.已知是线段的垂直平分线,下列说法中正确的是( )
A.与距离相等的点在MN上
B.与点和点距离相等的点在上
C.与距离相等的点在上
D.垂直平分
7.如图,直线l1∥l2,将等边三角形如图放置若∠α=25°,则∠β等于( )
A.35° B.30° C.25° D.20°
8.如图,已知:,,平分,,有下列结论:①;②;③;④.结论正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,三角形纸片ABC中,∠A=80°,∠B=60°,将纸片的角折叠,使点C落在△ABC内,若∠α=30°,则∠β的度数是( )
A. B. C. D.
10.如图,中,是的角平分线,延长至,使得,连接.下列判断:;;平分;的面积的面积,一定成立的个数是( )
A.个 B.个 C.个 D.个
二、填空题
11.如图,①在OA、OB上分别截取线段OD、OE,使OD=OE;②分别以为圆心,大于的长为半径画弧,在内两弧交于点;③作射线.若∠AOB=60°,则 .
12.如图,已知 为等边三角形, 为中线,延长 至 ,使 连接 ,则 的长是 .
13.如图,在中,,点,分别在边,上,,则的度数为 .
14.如图所示,将长方形纸片折叠,使点与点重合,点落在点处,折痕为,若,那么的度数为 .
15.如图,在中,,,点P是边上一动点,连接,在AP的上方作等边三角形,则周长的最小值为 .
16.如图,a∥b,∠ABC=50°,若△ABC是等腰三角形,则∠a= °。(填一个即可).
17.在等腰三角形ABC中,AB=AC,一腰上的中线BD将这个三角形的周长分成15cm和6cm两部分,这个等腰三角形的三边长为 .
三、解答题
18.已知点O为直线上一点,将直角三角板如图所示放置,且直角顶点在O处,在内部作射线,且恰好平分.
(1)若,求的度数;
(2)若,求的度数.
19.如图,直线,相交于点,,平分.若,求的度数.
20.如图,是的平分线,是的平分线.
(1)如果,,求的度数;
(2)如果,,求的度数;
21. 如图:在△ABC中,AB=AD=CD.
(1)若∠C=36°,求∠B的度数.
(2)若∠BAD=x°,∠C=y°, 求x和y的数量关系(用x的代数式表示y).
22.如图、直线、相交于点,于点,,平分,求的度数.
23.如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
答案解析部分
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】A
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】30
12.【答案】2
13.【答案】
14.【答案】125°
15.【答案】30
16.【答案】130(答案不唯一)
17.【答案】10cm,10cm,1cm
18.【答案】(1)
(2)
19.【答案】
20.【答案】(1)
(2)
21.【答案】(1)解:∵AD=CD
∴∠C=∠DAC=36°
∵∠ADB=∠C+∠DAC
∴∠ADB=36+36=72°
∵AB=AD
∴∠B=∠ADB =72°
(2)解:∵∠B+∠ADB+∠BAD=180°
∴∠B+∠ADB=(180-x)°
∵AB=AD
∴∠B=∠ADB =(90-x)°
∵AD=CD
∴∠C=∠DAC= y°
∵∠ADB=∠C+∠DAC
∴90-x=2y
∴y=45-x
22.【答案】
23.【答案】解:连接OA,OC,
∵OE,OF分别是AC,BD的垂直平分线,
∴OA=OC,OB=OD,
∵AB=CD,
∴△ABO≌△COD(SSS),
∴∠ABO=∠CDO,
设∠OBD=∠ODB=α,∠ABO=∠CDO=β,
∴α+β=120°,β﹣α=38°,
∴α=41°,
∴∠OBD=41°.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
