新2014-2015八年级下学期数学模拟试题四及答案
文档属性
| 名称 | 新2014-2015八年级下学期数学模拟试题四及答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 181.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-21 00:00:00 | ||
图片预览



文档简介
2014-2015学年八年级(下)期末数学模拟试卷四
一、单项选择题(共20小题,每小题3分,满分60分)
1.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B. ( http: / / www.21cnjy.com ) C. D.
2.下列各式是最简二次根式的是( )
A. B. C. D.
3.顺次连接对角线相等的四边形各边中点,所得四边形是( )
A. 矩形 B. 平行四边形 C. 菱形 D. 任意四边形
4.若a>b,则下列不等式不一定成立的是( )
A. a+m>b+m B. a(m2+1)>b(m2+1) C. D. a2>b2
5.下列计算正确的是( )
A. B. (﹣)2=9 C. =±16 D. ﹣(﹣)2=3
6.(3分)不等式组的解集在数轴上表示正确的是( )
A. B. C. D.
7.如图,△ABC的顶点坐标分别为A(4 ( http: / / www.21cnjy.com ),6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A的对应点A′的坐标是(
A. (﹣3,3) B. (3,﹣3) C. (﹣2,4) D. (1,4)
8.张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是( ) ( http: / / www.21cnjy.com )
A. 加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B. 途中加油21升
C. 汽车加油后还可行驶4小时
D. 汽车到达乙地时油箱中还余油6升
解:A、设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=kt+b.
将(0,25),(2,9)代入,
得,解得,
所以y=﹣8t+25,故A选项正确,但不符合题意;
B、由图象可知,途中加油:30﹣9=21(升),故B选项正确,但不符合题意;
C、由图可知汽车每小时用油(25﹣9)÷2=8(升),
所以汽车加油后还可行驶:30÷8=3<4(小时),故C选项错误,但符合题意;
D、∵汽车从甲地到达乙地,所需时间为:500÷100=5(小时),
∴5小时耗油量为:8×5=40(升),
又∵汽车出发前油箱有油25升,途中加油21升,
∴汽车到达乙地时油箱中还余油:25+21﹣40=6(升),故D选项正确,但不符合题意.
故选:C.
9.函数y=中的自变量x的取值范围是( )
A. x≥0 B. x≠﹣1 C. x>0 D. x≥0且x≠﹣1
10.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
( http: / / www.21cnjy.com )
A. 45° B. 55° C. 60° D. 75°
11.如果ab>0,a+b<0,那么下面各式:①=,② =1,③÷=﹣b,其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
12.如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=x上一点,则点B与其对应点B′间的距离为( ) ( http: / / www.21cnjy.com )
A. B. 3 C. 4 D. 5
13.计算的结果是( )
A. B. C. D.
14.若关于x的一元一次不等式组无解,则a的取值范围是( )
A. a≥1 B. a>1 C. a≤﹣1 D. a<﹣1
15.如图,已知直线y1=x+m与y2= ( http: / / www.21cnjy.com )kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m>kx﹣1的解集在数轴上表示正确的是( )
A. B. C. D.
16.用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
甲种原料 乙种原料
维生素C含量(单位 千克) 600 100
原料价格(元 千克) 8 4
现配制这种饮料10kg,要求至少含有4200单位的维生素C,若所需甲种原料的质量为x kg,则x应满足的不等式为( )
A. 600x+100(10﹣x)≥4200 B. 8x+4(100﹣x)≤4200
C. 600x+100(10﹣x)≤4200 D. 8x+4(100﹣x)≥4200
17.如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
( http: / / www.21cnjy.com )
A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
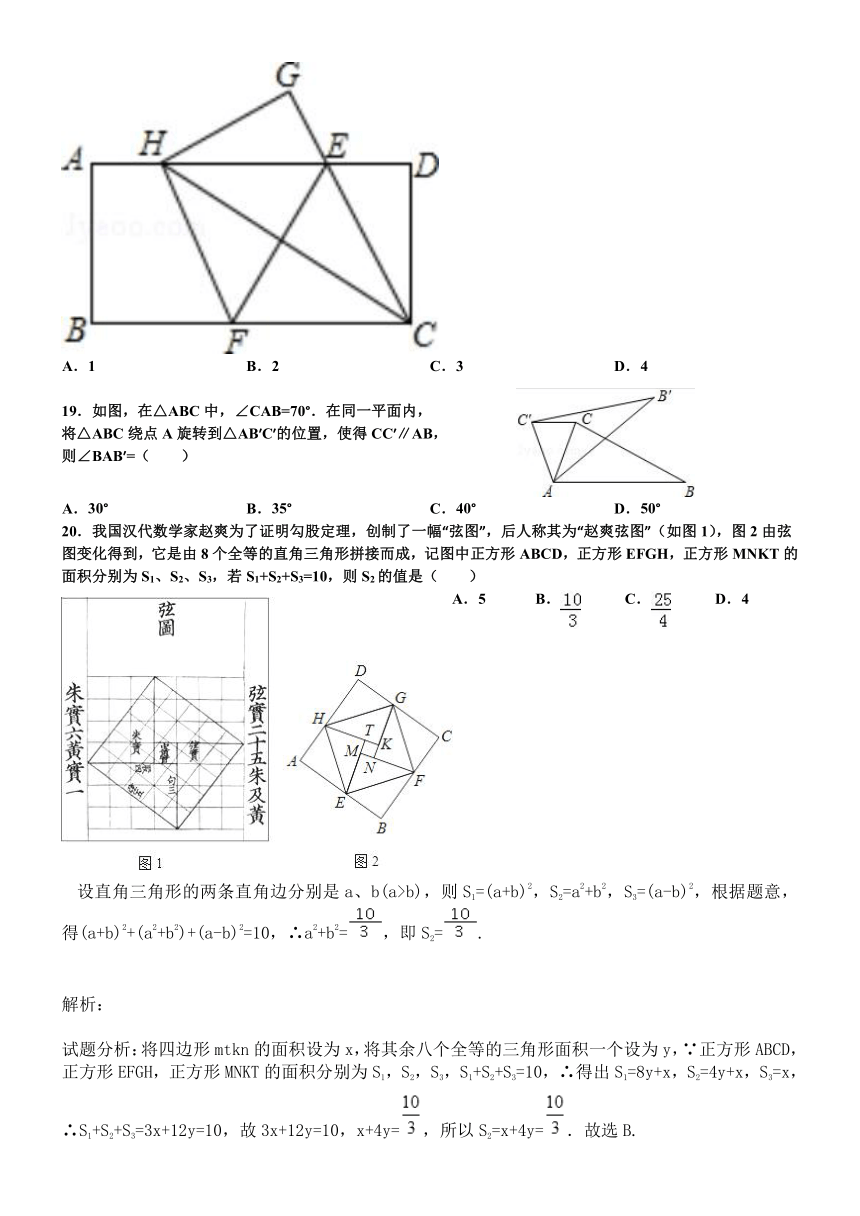
18.如图,在一张矩形纸片ABCD中,A ( http: / / www.21cnjy.com )B=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2.
以上结论中,你认为正确的有( )个.
( http: / / www.21cnjy.com )
A. 1 B. 2 C. 3 D. 4
19.如图,在△ABC中,∠CAB=70°.在同一平面内,
将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,
则∠BAB′=( )
A. 30° B. 35° C. 40° D. 50°
20.我国汉代数学家赵爽为 ( http: / / www.21cnjy.com )了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1),图2由弦图变化得到,它是由8个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1、S2、S3,若S1+S2+S3=10,则S2的值是( )
( http: / / www.21cnjy.com ) A. 5 B. C. D. 4
设直角三角形的两条直角边分别是a、b(a>b),则S1=(a+b)2,S2=a2+b2,S3=(a-b)2,根据题意,得(a+b)2+(a2+b2)+(a-b)2=10,∴a2+b2=,即S2=.
解析:
试题分析:将四边形mtkn的面积设为x,将其余八个全等的三角形面积一个设为y,∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=10,∴得出S1=8y+x,S2=4y+x,S3=x,∴S1+S2+S3=3x+12y=10,故3x+12y=10,x+4y=,所以S2=x+4y=.故选B.
考点:勾股定理的证明.
点评:此题要求熟练掌握图形面积关系,根据已知得出用x,y表示出S1,S2,S3,再利用S1+S2+S3=10求出是解决问题的关键.
二、填空题(共4小题,每小题3分,满分12分)
21.已知两条线段的长分别为和,当第三条线段的长取 时,这三条线段能围成一个直角三角形.
22.如图,将一朵小花放置在平面直角坐 ( http: / / www.21cnjy.com )标系中第三象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向下平移2个单位长到丙位置,则小花顶点A在丙位置中的对应点A′的坐标为 .
( http: / / www.21cnjy.com )
23.直线y=2x+8,y=﹣2x﹣4与y轴所围成的图形的面积为 .
24.如图,正方形ABCD的面积 ( http: / / www.21cnjy.com )为256,点F在AD上,点E在AB的延长线上,FC⊥CE,直角三角形CEF的面积为200,则DF= .
( http: / / www.21cnjy.com )
一、单项选择题(共20小题,每小题3分,满分60分)
1.B 2.B 3.C 4.D 5 ( http: / / www.21cnjy.com ).A 6.B 7.A 8.C 9.A 10.C 11.B 12.C 13.B 14.A 15.D 16.A 17.C 18.C 19.C 20.B
二、填空题(共4小题,每小题3分,满分12分)
21.2或4 22.(3,-1) 23.18 24.12
三、解答题(共5小题,共48分)
25.(1)计算:(2﹣)2013(2+)2014﹣2|﹣|﹣(﹣)0﹣÷﹣.
解:(1)原式=[(2﹣)(2+)]2013 (2+)﹣2×﹣1﹣﹣3
=2+﹣﹣1﹣﹣3
=1﹣;
(2)已知关于x的不等式组共有5个整数解,求a的取值范围.
解:
(2),
解①得x<1,
解②得x≥a+3,
所以不等式组的解集为a+3≤x<1,
因为不等式组共有5个整数解,即不等式组的整数解为0,﹣1,﹣2,﹣3,﹣4,
所以﹣5<a+3≤﹣4,
解得﹣8<a≤﹣7.
26.在正方形网格中建立如图所示的平面直角坐标系xoy.△ABC的三个顶点都在格点上,点A的坐标是(4,4 ),请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.
( http: / / www.21cnjy.com )
27.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,
并证明你的结论.
28.已知甲、乙两种原料中均含有A元素,其含量及每吨原料的购买单价如下表所示:
A元素含量 单价(万元/吨)
甲原料 5% 2.5
乙原料 8% 6
已知用甲原料提取每千克A元素要排放废气1吨, ( http: / / www.21cnjy.com )用乙原料提取每千克A元素要排放废气0.5吨,若某厂要提取A元素20千克,并要求废气排放不超过16吨,问:该厂购买这两种原料的费用最少是多少万元?
分析:设需要甲原料x吨, ( http: / / www.21cnjy.com )乙原料y吨.由20千克=0.02吨就可以列出方程5%x+8%y=0.02和不等式5%x×1000x1+8%y×1000x0.5≤16,设购买这两种原料的费用为W万元,根据条件可以列出表达式,由函数的性质就可以得出结论。
【解析】
设需要甲原料x吨,乙原料y吨,
由题意,得,即。
∴y≥0.1。
设这两种原料的费用为W万元,由题意,得
。
∵k=2>0,∴W随x的增大而增大。
∴y =0.1时,W最小=1.2。
答:该厂购买这两种原料的费用最少为1.2万元。
29.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
求证:四边形BCDE是矩形.
( http: / / www.21cnjy.com )
一、单项选择题(共20小题,每小题3分,满分60分)
1.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B. ( http: / / www.21cnjy.com ) C. D.
2.下列各式是最简二次根式的是( )
A. B. C. D.
3.顺次连接对角线相等的四边形各边中点,所得四边形是( )
A. 矩形 B. 平行四边形 C. 菱形 D. 任意四边形
4.若a>b,则下列不等式不一定成立的是( )
A. a+m>b+m B. a(m2+1)>b(m2+1) C. D. a2>b2
5.下列计算正确的是( )
A. B. (﹣)2=9 C. =±16 D. ﹣(﹣)2=3
6.(3分)不等式组的解集在数轴上表示正确的是( )
A. B. C. D.
7.如图,△ABC的顶点坐标分别为A(4 ( http: / / www.21cnjy.com ),6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A的对应点A′的坐标是(
A. (﹣3,3) B. (3,﹣3) C. (﹣2,4) D. (1,4)
8.张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是( ) ( http: / / www.21cnjy.com )
A. 加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B. 途中加油21升
C. 汽车加油后还可行驶4小时
D. 汽车到达乙地时油箱中还余油6升
解:A、设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=kt+b.
将(0,25),(2,9)代入,
得,解得,
所以y=﹣8t+25,故A选项正确,但不符合题意;
B、由图象可知,途中加油:30﹣9=21(升),故B选项正确,但不符合题意;
C、由图可知汽车每小时用油(25﹣9)÷2=8(升),
所以汽车加油后还可行驶:30÷8=3<4(小时),故C选项错误,但符合题意;
D、∵汽车从甲地到达乙地,所需时间为:500÷100=5(小时),
∴5小时耗油量为:8×5=40(升),
又∵汽车出发前油箱有油25升,途中加油21升,
∴汽车到达乙地时油箱中还余油:25+21﹣40=6(升),故D选项正确,但不符合题意.
故选:C.
9.函数y=中的自变量x的取值范围是( )
A. x≥0 B. x≠﹣1 C. x>0 D. x≥0且x≠﹣1
10.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
( http: / / www.21cnjy.com )
A. 45° B. 55° C. 60° D. 75°
11.如果ab>0,a+b<0,那么下面各式:①=,② =1,③÷=﹣b,其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
12.如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=x上一点,则点B与其对应点B′间的距离为( ) ( http: / / www.21cnjy.com )
A. B. 3 C. 4 D. 5
13.计算的结果是( )
A. B. C. D.
14.若关于x的一元一次不等式组无解,则a的取值范围是( )
A. a≥1 B. a>1 C. a≤﹣1 D. a<﹣1
15.如图,已知直线y1=x+m与y2= ( http: / / www.21cnjy.com )kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m>kx﹣1的解集在数轴上表示正确的是( )
A. B. C. D.
16.用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
甲种原料 乙种原料
维生素C含量(单位 千克) 600 100
原料价格(元 千克) 8 4
现配制这种饮料10kg,要求至少含有4200单位的维生素C,若所需甲种原料的质量为x kg,则x应满足的不等式为( )
A. 600x+100(10﹣x)≥4200 B. 8x+4(100﹣x)≤4200
C. 600x+100(10﹣x)≤4200 D. 8x+4(100﹣x)≥4200
17.如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
( http: / / www.21cnjy.com )
A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
18.如图,在一张矩形纸片ABCD中,A ( http: / / www.21cnjy.com )B=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2.
以上结论中,你认为正确的有( )个.
( http: / / www.21cnjy.com )
A. 1 B. 2 C. 3 D. 4
19.如图,在△ABC中,∠CAB=70°.在同一平面内,
将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,
则∠BAB′=( )
A. 30° B. 35° C. 40° D. 50°
20.我国汉代数学家赵爽为 ( http: / / www.21cnjy.com )了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1),图2由弦图变化得到,它是由8个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1、S2、S3,若S1+S2+S3=10,则S2的值是( )
( http: / / www.21cnjy.com ) A. 5 B. C. D. 4
设直角三角形的两条直角边分别是a、b(a>b),则S1=(a+b)2,S2=a2+b2,S3=(a-b)2,根据题意,得(a+b)2+(a2+b2)+(a-b)2=10,∴a2+b2=,即S2=.
解析:
试题分析:将四边形mtkn的面积设为x,将其余八个全等的三角形面积一个设为y,∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=10,∴得出S1=8y+x,S2=4y+x,S3=x,∴S1+S2+S3=3x+12y=10,故3x+12y=10,x+4y=,所以S2=x+4y=.故选B.
考点:勾股定理的证明.
点评:此题要求熟练掌握图形面积关系,根据已知得出用x,y表示出S1,S2,S3,再利用S1+S2+S3=10求出是解决问题的关键.
二、填空题(共4小题,每小题3分,满分12分)
21.已知两条线段的长分别为和,当第三条线段的长取 时,这三条线段能围成一个直角三角形.
22.如图,将一朵小花放置在平面直角坐 ( http: / / www.21cnjy.com )标系中第三象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向下平移2个单位长到丙位置,则小花顶点A在丙位置中的对应点A′的坐标为 .
( http: / / www.21cnjy.com )
23.直线y=2x+8,y=﹣2x﹣4与y轴所围成的图形的面积为 .
24.如图,正方形ABCD的面积 ( http: / / www.21cnjy.com )为256,点F在AD上,点E在AB的延长线上,FC⊥CE,直角三角形CEF的面积为200,则DF= .
( http: / / www.21cnjy.com )
一、单项选择题(共20小题,每小题3分,满分60分)
1.B 2.B 3.C 4.D 5 ( http: / / www.21cnjy.com ).A 6.B 7.A 8.C 9.A 10.C 11.B 12.C 13.B 14.A 15.D 16.A 17.C 18.C 19.C 20.B
二、填空题(共4小题,每小题3分,满分12分)
21.2或4 22.(3,-1) 23.18 24.12
三、解答题(共5小题,共48分)
25.(1)计算:(2﹣)2013(2+)2014﹣2|﹣|﹣(﹣)0﹣÷﹣.
解:(1)原式=[(2﹣)(2+)]2013 (2+)﹣2×﹣1﹣﹣3
=2+﹣﹣1﹣﹣3
=1﹣;
(2)已知关于x的不等式组共有5个整数解,求a的取值范围.
解:
(2),
解①得x<1,
解②得x≥a+3,
所以不等式组的解集为a+3≤x<1,
因为不等式组共有5个整数解,即不等式组的整数解为0,﹣1,﹣2,﹣3,﹣4,
所以﹣5<a+3≤﹣4,
解得﹣8<a≤﹣7.
26.在正方形网格中建立如图所示的平面直角坐标系xoy.△ABC的三个顶点都在格点上,点A的坐标是(4,4 ),请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.
( http: / / www.21cnjy.com )
27.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,
并证明你的结论.
28.已知甲、乙两种原料中均含有A元素,其含量及每吨原料的购买单价如下表所示:
A元素含量 单价(万元/吨)
甲原料 5% 2.5
乙原料 8% 6
已知用甲原料提取每千克A元素要排放废气1吨, ( http: / / www.21cnjy.com )用乙原料提取每千克A元素要排放废气0.5吨,若某厂要提取A元素20千克,并要求废气排放不超过16吨,问:该厂购买这两种原料的费用最少是多少万元?
分析:设需要甲原料x吨, ( http: / / www.21cnjy.com )乙原料y吨.由20千克=0.02吨就可以列出方程5%x+8%y=0.02和不等式5%x×1000x1+8%y×1000x0.5≤16,设购买这两种原料的费用为W万元,根据条件可以列出表达式,由函数的性质就可以得出结论。
【解析】
设需要甲原料x吨,乙原料y吨,
由题意,得,即。
∴y≥0.1。
设这两种原料的费用为W万元,由题意,得
。
∵k=2>0,∴W随x的增大而增大。
∴y =0.1时,W最小=1.2。
答:该厂购买这两种原料的费用最少为1.2万元。
29.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
求证:四边形BCDE是矩形.
( http: / / www.21cnjy.com )
同课章节目录
