圆的标准方程
图片预览








文档简介
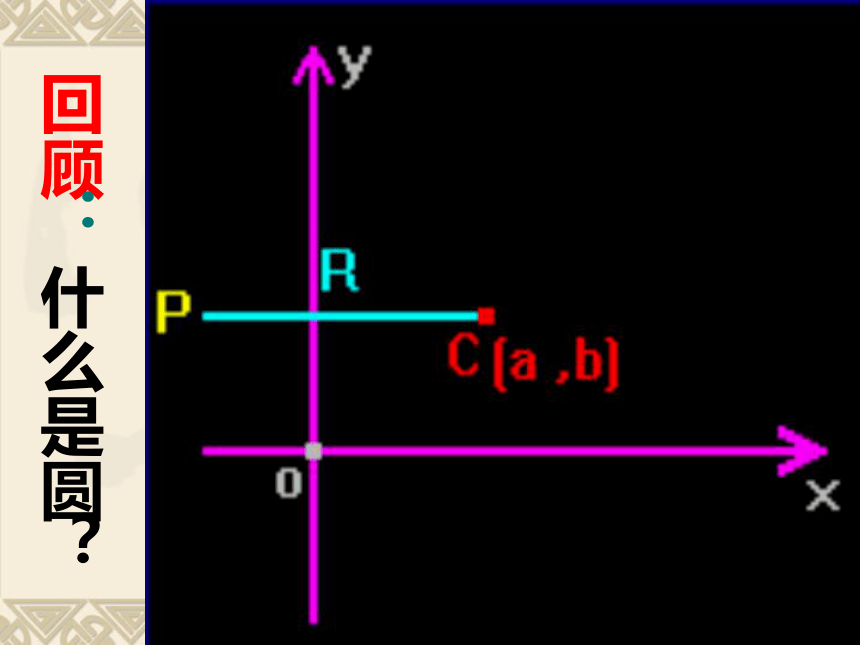
课件21张PPT。圆的标准方程高二数学组欣赏自然的和谐美一.情境设置自然界中有着漂亮的圆,圆是最完美的曲线之一.二.学生活动欣赏上述美景,你有何感想?回顾:什么是圆?圆的定义:平面内与定点距离等于定长的点的集合(轨迹)是圆.
问题1--什么是做圆?问题2--确定圆需要哪几个要素?圆心--确定圆的位置半径--确定圆的大小问题3--圆心为(a,b),半经为r的方程是什么呢?定点就是圆心,定长就是半径。探索:圆心是C(a,b),半径是r的圆的方程是什么?解:设P(x,y)是圆C上任意一点,则 CP=r.三.建构数学建构圆的标准方程由两点间距离公式可得:(x-a) 2 + (y-b) 2 = r2反过来,若点P1的坐标(x1,y1)是方程(二元二次方程)(x1-a) 2 + (y1-b) 2 = r2的解,那么 即有:这说明点P1(x1,y1)在以C(a,b)为圆心,
r为半径的圆上.圆的标准方程 特点:1、 明确给出了圆心坐标和半径.
2、确定圆的方程必须具备三个独立条件,
即a、b、r .
3、是关于x、y的二元二次方程.
4.若圆心在坐标原点,则圆方程为x2+y2=r2.
问题:观察圆的标准方程的特点有哪些?例1:试写出下列圆 (x-1)2+(y-3)2=9的圆心及半径.变式1:判断下列方程是否为圆的方程如果是的写出下
列各圆的圆心坐标和半径.
(1) (x-1)2+y2=6 (2) (x+1)2-(y-2)2=9
(3)x2+(y+3)2=0 (4)(x+a)2+y2=a2
解:圆心为点(1,3)半径为r=3四.数学运用确定圆的标准方程变式2:写出下列圆的标准方程:(1)圆心在原点,半径为6 ; (2)圆心在原点,经过点(0,-3); (3)经过原点 ,圆心为C(2,0).解: (1)x2+y2=36
(2)x2+y2=9
(3)(x-2)2+y2=4例2:求圆心是C(2,-3),且经过原点的圆的标准方程.解:因为圆C经过坐标原点,所以圆C的半径是
= =
方程为: (x-2) 2 + (y+3) 2 = 13变式1:求圆心在(-2,3)又过点(1,7)的圆的方程.解:圆的半径r= =5
圆的方程为: (x+2) 2 + (y-3) 2 = 25变式2:求以点C(-1,-5)为圆心,并且和y轴相切的圆的标准方程.变式3:已知点A(-4,-5),B(6,-1),求以线段AB为直径的圆的标准方程.解:圆的半径r= 1 ,圆的方程为: (x+1) 2 + (y+5) 2 =1解:圆心为(1,-3)半径为r= ,圆 的方程为:(x-1)2+(y+3)2=29变式4:直线x+y=4和x-y=-2均过圆心,半径为3的圆的标准方程是什么?变式5:求圆心在(1,3),且和直线3x-4y-7=0相切的圆的标准方程. 解:由 得 则圆心为(1,3)
所以圆的方程为:(x-1) 2 + (y-3) 2 = 9解:圆的半径r= =
圆的方程为: (x-1) 2 + (y-3) 2 =例3.已知隧道的截面是半径为4米的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7米,高为3米的货车能不能驶入这个隧道?解:以某一截面半圆的圆心为坐标原
点,半圆的直径AB所在的直线为
x轴,建立直角坐标系(如右图)
将x=2.7代入,得 <3。 那么半圆的方程为即在离中心线2.7米处,隧道的高度低于货车的高度.
因此,货车不能驶入这个隧道.
(1)圆心为C(a,b),半径为r的圆的标准方程为 (x-a)2+(y-b)2=r2
当圆心在原点时 a=b=0,圆的标准方程为:x2+y2=r2
(2)由于圆的标准方程中含有 a,b,r三个参数,因此必须具备三个独立的条件才能确定圆;对于由已知条件容易求得圆心坐标和圆的半径或需利用圆心坐标列方程的问题一般采用圆的标准方程.
(3)注意圆的平面几何知识的运用以及应用圆的方程解决实际问题.五.课堂小结学案的第十四课时的课后作业已知:一个圆的直径端点是 ,证明:圆的方程是六.课后作业七.课后思考题
问题1--什么是做圆?问题2--确定圆需要哪几个要素?圆心--确定圆的位置半径--确定圆的大小问题3--圆心为(a,b),半经为r的方程是什么呢?定点就是圆心,定长就是半径。探索:圆心是C(a,b),半径是r的圆的方程是什么?解:设P(x,y)是圆C上任意一点,则 CP=r.三.建构数学建构圆的标准方程由两点间距离公式可得:(x-a) 2 + (y-b) 2 = r2反过来,若点P1的坐标(x1,y1)是方程(二元二次方程)(x1-a) 2 + (y1-b) 2 = r2的解,那么 即有:这说明点P1(x1,y1)在以C(a,b)为圆心,
r为半径的圆上.圆的标准方程 特点:1、 明确给出了圆心坐标和半径.
2、确定圆的方程必须具备三个独立条件,
即a、b、r .
3、是关于x、y的二元二次方程.
4.若圆心在坐标原点,则圆方程为x2+y2=r2.
问题:观察圆的标准方程的特点有哪些?例1:试写出下列圆 (x-1)2+(y-3)2=9的圆心及半径.变式1:判断下列方程是否为圆的方程如果是的写出下
列各圆的圆心坐标和半径.
(1) (x-1)2+y2=6 (2) (x+1)2-(y-2)2=9
(3)x2+(y+3)2=0 (4)(x+a)2+y2=a2
解:圆心为点(1,3)半径为r=3四.数学运用确定圆的标准方程变式2:写出下列圆的标准方程:(1)圆心在原点,半径为6 ; (2)圆心在原点,经过点(0,-3); (3)经过原点 ,圆心为C(2,0).解: (1)x2+y2=36
(2)x2+y2=9
(3)(x-2)2+y2=4例2:求圆心是C(2,-3),且经过原点的圆的标准方程.解:因为圆C经过坐标原点,所以圆C的半径是
= =
方程为: (x-2) 2 + (y+3) 2 = 13变式1:求圆心在(-2,3)又过点(1,7)的圆的方程.解:圆的半径r= =5
圆的方程为: (x+2) 2 + (y-3) 2 = 25变式2:求以点C(-1,-5)为圆心,并且和y轴相切的圆的标准方程.变式3:已知点A(-4,-5),B(6,-1),求以线段AB为直径的圆的标准方程.解:圆的半径r= 1 ,圆的方程为: (x+1) 2 + (y+5) 2 =1解:圆心为(1,-3)半径为r= ,圆 的方程为:(x-1)2+(y+3)2=29变式4:直线x+y=4和x-y=-2均过圆心,半径为3的圆的标准方程是什么?变式5:求圆心在(1,3),且和直线3x-4y-7=0相切的圆的标准方程. 解:由 得 则圆心为(1,3)
所以圆的方程为:(x-1) 2 + (y-3) 2 = 9解:圆的半径r= =
圆的方程为: (x-1) 2 + (y-3) 2 =例3.已知隧道的截面是半径为4米的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7米,高为3米的货车能不能驶入这个隧道?解:以某一截面半圆的圆心为坐标原
点,半圆的直径AB所在的直线为
x轴,建立直角坐标系(如右图)
将x=2.7代入,得 <3。 那么半圆的方程为即在离中心线2.7米处,隧道的高度低于货车的高度.
因此,货车不能驶入这个隧道.
(1)圆心为C(a,b),半径为r的圆的标准方程为 (x-a)2+(y-b)2=r2
当圆心在原点时 a=b=0,圆的标准方程为:x2+y2=r2
(2)由于圆的标准方程中含有 a,b,r三个参数,因此必须具备三个独立的条件才能确定圆;对于由已知条件容易求得圆心坐标和圆的半径或需利用圆心坐标列方程的问题一般采用圆的标准方程.
(3)注意圆的平面几何知识的运用以及应用圆的方程解决实际问题.五.课堂小结学案的第十四课时的课后作业已知:一个圆的直径端点是 ,证明:圆的方程是六.课后作业七.课后思考题
