1.3线段垂直平分线课件(第1课时)(23张PPT)
文档属性
| 名称 | 1.3线段垂直平分线课件(第1课时)(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-21 00:00:00 | ||
图片预览





文档简介
课件23张PPT。 1.3 线段的垂直平分线
第1课时 线段的垂直平分线学习目标:
1.理解线段垂直平分线的性质和判定.
2.能运用线段垂直平分线的性质和判定解决实际问
题.
3.会用尺规经过已知直线外一点作这条直线的垂线,
了解作图的道理.
学习重点:
线段垂直平分线的性质及尺规经过已知直线外一点作这条直线的垂线.
一、创设情境,温故知新 1.线段是轴对称图形吗?什么是线段的垂直平分线?
2.你能找出线段的对称轴吗?
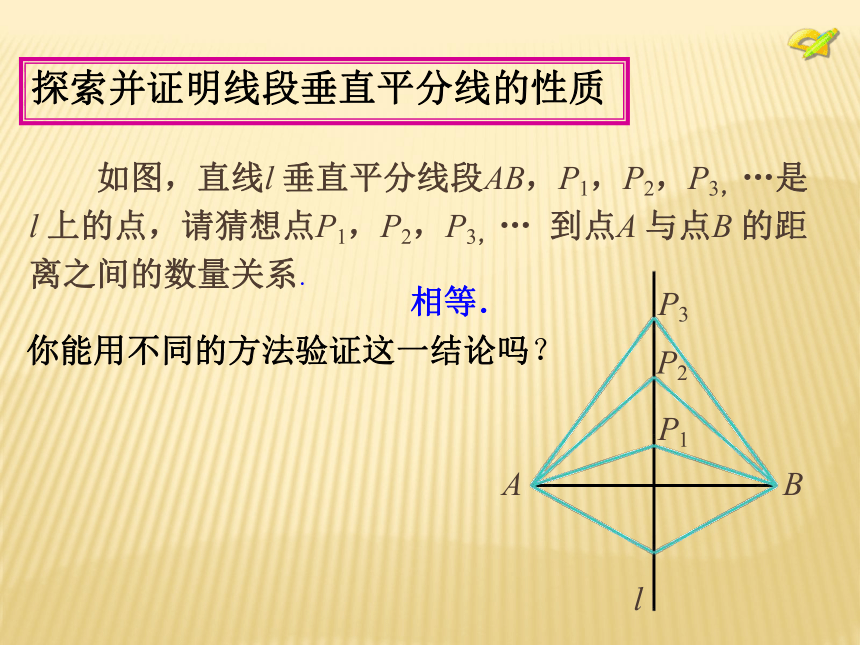
3. 线段的对称轴与这条线段有什么关系?说明理由.你能用不同的方法验证这一结论吗?探索并证明线段垂直平分线的性质 如图,直线l 垂直平分线段AB,P1,P2,P3,…是
l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距
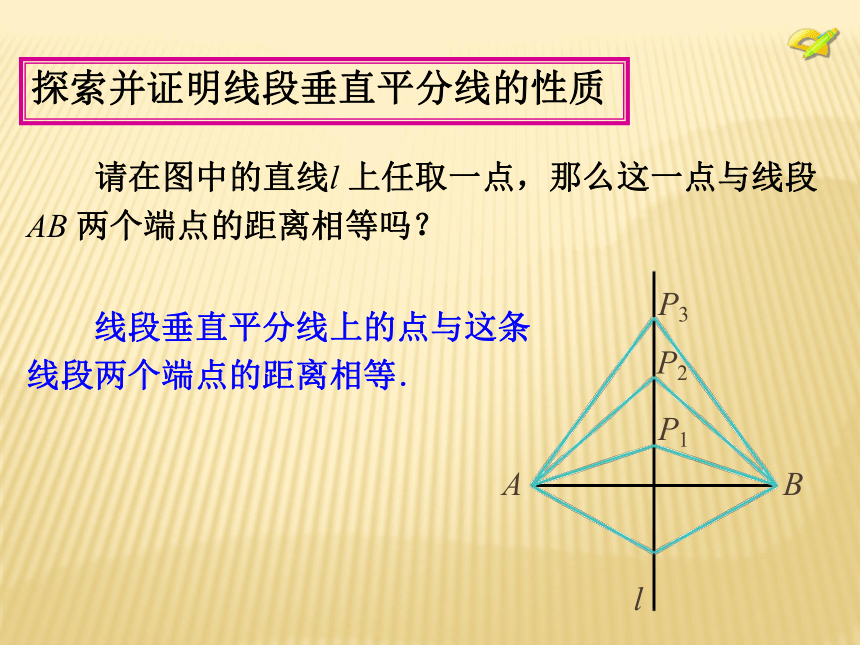
离之间的数量关系. 相等. 探索并证明线段垂直平分线的性质 请在图中的直线l 上任取一点,那么这一点与线段
AB 两个端点的距离相等吗? 线段垂直平分线上的点与这条
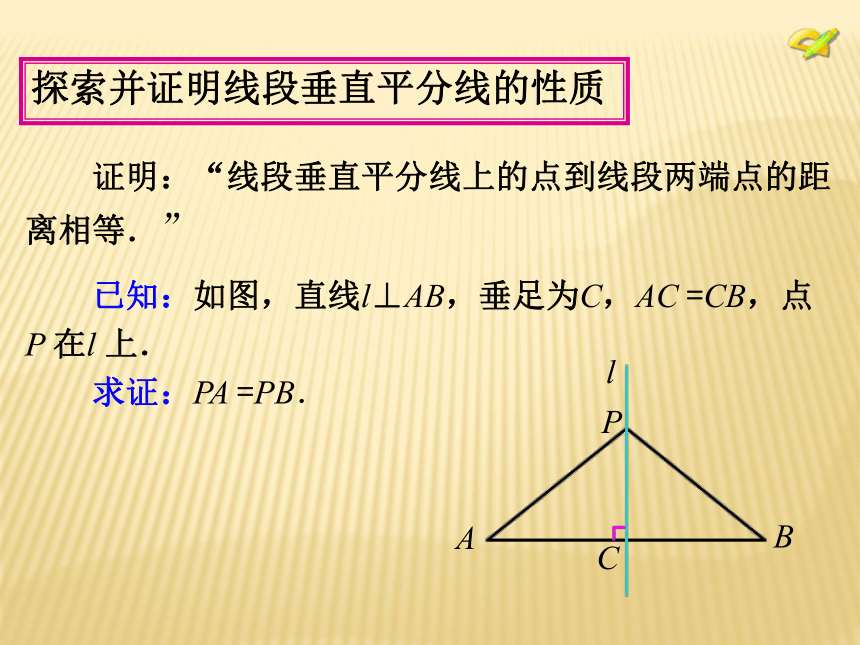
线段两个端点的距离相等. 已知:如图,直线l⊥AB,垂足为C,AC =CB,点
P 在l 上.
求证:PA =PB.探索并证明线段垂直平分线的性质 证明:“线段垂直平分线上的点到线段两端点的距
离相等.”探索并证明线段垂直平分线的性质用几何语言表示为:
∵ CA =CB,l⊥AB,
∴ PA =PB.证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS) ∴ PA =PB.线段垂直平分线的性质:
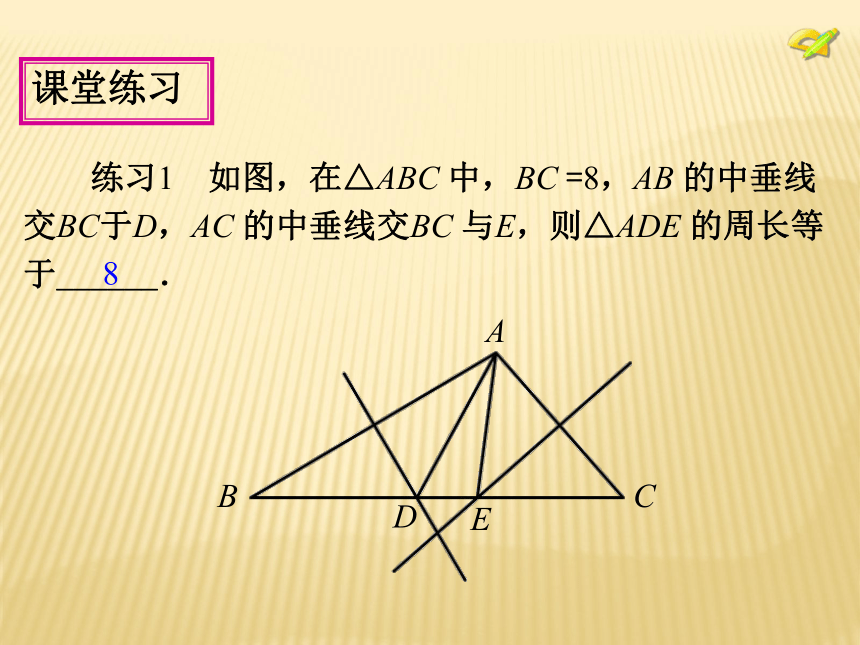
线段垂直平分线上的点与这条线段两个端点的距离相等.已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.8课堂练习 练习1 如图,在△ABC 中,BC =8,AB 的中垂线
交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等
于______.
线段的垂直平分线我们曾经利用折纸的方法得到:
线段垂直平分线上的点到这条线段两个端点距离相等.
你能证明这一结论吗?已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.分析:(1)要证明PA=PB,而△APC≌△BPC的条件由已知 故结论可证.老师期望:你能写出规范的证明过程.AC=BC,MN⊥AB,可推知其能满足公理(SAS).就需要证明PA,PB所在的△APC≌△BPC,进步的标志′驶向胜利的彼岸你能写出“定理 线段垂直平分线上的点到这条线段两个端点距离相等”的逆命题吗?
逆命题 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.它是真命题吗?如果是.请你证明它.已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.分析:要证明点P在线段AB的垂直平分线上,可以先作出过点P的AB的垂线(或AB的中线,),然后证明另一个结论正确.想一想:若作出∠P的角平分线,结论是否也可以得证?进步的标志′驶向胜利的彼岸你能写出“定理 线段垂直平分线上的点到这条线段两个端点距离相等”的逆命题吗?
逆命题 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.它是真命题吗?如果是.请你证明它.已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.分析:要证明点P在线段AB的垂直平分线上,可以先作出过点P的AB的垂线(或AB的中线,),然后证明另一个结论正确.想一想:若作出∠P的角平分线,结论是否也可以得证?解:∵ AD⊥BC,BD =DC
∴ AD 是BC 的垂直平分线
∴ AB =AC
∵ 点C 在AE 的垂直平分线上
∴ AC =CE. ∴ AB =AC =CE课堂练习P622 如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?∵ AB =CE,BD =DC,∴ AB +BD =CD +CE.
即 AB +BD =DE .探索并证明线段垂直平分线的判定 反过来,如果PA =PB,那么点P 是否在线段AB 的
垂直平分线上呢? 点P 在线段AB 的垂直平分线上. 已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.探索并证明线段垂直平分线的判定证明:如图作PC⊥AB
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上已知:如图,PA =PB.求证:点P 在线段AB 的垂直平分线上.探索并证明线段垂直平分线的判定用几何符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上. 线段垂直平分线的判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 这些点能组成什么几何图形? 探索并证明线段垂直平分线的判定 你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点? 在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、
B 的距离相等的所有点的集合.解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上∴ 直线AM 是线段BC 的垂直
平分线.课堂练习P62 2 练习3 如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?(1)为什么任意取一点K ,使点K与点C 在直线两旁?尺规作图 (P62) 如何用尺规作图的方法经过直线外一点作已知直线的垂线?(2)为什么要以大于 的长为半径作弧? (3)为什么直线CF 就是所求作的垂线?(1)你学会了什么数学知识?它是怎样得到的?它能帮助你解决什么问题?
(2)线段垂直平分线的性质和判定是如何得到的?
两者之间有什么关系?
(3)如何判断一条直线是否是线段的垂直平分线? 课堂小结 理清知识六.达标测评 1.如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=______
2.如图,AB=AC=8cm,AB的垂直平分线交AC于D,若△ADB的周长为18,则DC=______3.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6 B.5 C.4 D.3
4.如图,△ABC中AC⊥DC,AD平分∠BAC,DE⊥AB于E,求证:直线AD是CE的垂直平分线.
习题1.6 驶向胜利的彼岸3.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长. 老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去. 布置作业教材习题;
第1课时 线段的垂直平分线学习目标:
1.理解线段垂直平分线的性质和判定.
2.能运用线段垂直平分线的性质和判定解决实际问
题.
3.会用尺规经过已知直线外一点作这条直线的垂线,
了解作图的道理.
学习重点:
线段垂直平分线的性质及尺规经过已知直线外一点作这条直线的垂线.
一、创设情境,温故知新 1.线段是轴对称图形吗?什么是线段的垂直平分线?
2.你能找出线段的对称轴吗?
3. 线段的对称轴与这条线段有什么关系?说明理由.你能用不同的方法验证这一结论吗?探索并证明线段垂直平分线的性质 如图,直线l 垂直平分线段AB,P1,P2,P3,…是
l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距
离之间的数量关系. 相等. 探索并证明线段垂直平分线的性质 请在图中的直线l 上任取一点,那么这一点与线段
AB 两个端点的距离相等吗? 线段垂直平分线上的点与这条
线段两个端点的距离相等. 已知:如图,直线l⊥AB,垂足为C,AC =CB,点
P 在l 上.
求证:PA =PB.探索并证明线段垂直平分线的性质 证明:“线段垂直平分线上的点到线段两端点的距
离相等.”探索并证明线段垂直平分线的性质用几何语言表示为:
∵ CA =CB,l⊥AB,
∴ PA =PB.证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS) ∴ PA =PB.线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.8课堂练习 练习1 如图,在△ABC 中,BC =8,AB 的中垂线
交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等
于______.
线段的垂直平分线我们曾经利用折纸的方法得到:
线段垂直平分线上的点到这条线段两个端点距离相等.
你能证明这一结论吗?已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.求证:PA=PB.分析:(1)要证明PA=PB,而△APC≌△BPC的条件由已知 故结论可证.老师期望:你能写出规范的证明过程.AC=BC,MN⊥AB,可推知其能满足公理(SAS).就需要证明PA,PB所在的△APC≌△BPC,进步的标志′驶向胜利的彼岸你能写出“定理 线段垂直平分线上的点到这条线段两个端点距离相等”的逆命题吗?
逆命题 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.它是真命题吗?如果是.请你证明它.已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.分析:要证明点P在线段AB的垂直平分线上,可以先作出过点P的AB的垂线(或AB的中线,),然后证明另一个结论正确.想一想:若作出∠P的角平分线,结论是否也可以得证?进步的标志′驶向胜利的彼岸你能写出“定理 线段垂直平分线上的点到这条线段两个端点距离相等”的逆命题吗?
逆命题 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.它是真命题吗?如果是.请你证明它.已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.分析:要证明点P在线段AB的垂直平分线上,可以先作出过点P的AB的垂线(或AB的中线,),然后证明另一个结论正确.想一想:若作出∠P的角平分线,结论是否也可以得证?解:∵ AD⊥BC,BD =DC
∴ AD 是BC 的垂直平分线
∴ AB =AC
∵ 点C 在AE 的垂直平分线上
∴ AC =CE. ∴ AB =AC =CE课堂练习P622 如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?∵ AB =CE,BD =DC,∴ AB +BD =CD +CE.
即 AB +BD =DE .探索并证明线段垂直平分线的判定 反过来,如果PA =PB,那么点P 是否在线段AB 的
垂直平分线上呢? 点P 在线段AB 的垂直平分线上. 已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.探索并证明线段垂直平分线的判定证明:如图作PC⊥AB
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上已知:如图,PA =PB.求证:点P 在线段AB 的垂直平分线上.探索并证明线段垂直平分线的判定用几何符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上. 线段垂直平分线的判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 这些点能组成什么几何图形? 探索并证明线段垂直平分线的判定 你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点? 在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、
B 的距离相等的所有点的集合.解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上∴ 直线AM 是线段BC 的垂直
平分线.课堂练习P62 2 练习3 如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?(1)为什么任意取一点K ,使点K与点C 在直线两旁?尺规作图 (P62) 如何用尺规作图的方法经过直线外一点作已知直线的垂线?(2)为什么要以大于 的长为半径作弧? (3)为什么直线CF 就是所求作的垂线?(1)你学会了什么数学知识?它是怎样得到的?它能帮助你解决什么问题?
(2)线段垂直平分线的性质和判定是如何得到的?
两者之间有什么关系?
(3)如何判断一条直线是否是线段的垂直平分线? 课堂小结 理清知识六.达标测评 1.如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=______
2.如图,AB=AC=8cm,AB的垂直平分线交AC于D,若△ADB的周长为18,则DC=______3.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6 B.5 C.4 D.3
4.如图,△ABC中AC⊥DC,AD平分∠BAC,DE⊥AB于E,求证:直线AD是CE的垂直平分线.
习题1.6 驶向胜利的彼岸3.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长. 老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去. 布置作业教材习题;
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
