沪科版数学八年级上册 第15章轴对称图形和等腰三角形 综合测试卷(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 第15章轴对称图形和等腰三角形 综合测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1017.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 00:00:00 | ||
图片预览


文档简介
第15 章综合测试卷
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题。(本大题共10小题,每小题4分,满分40分)
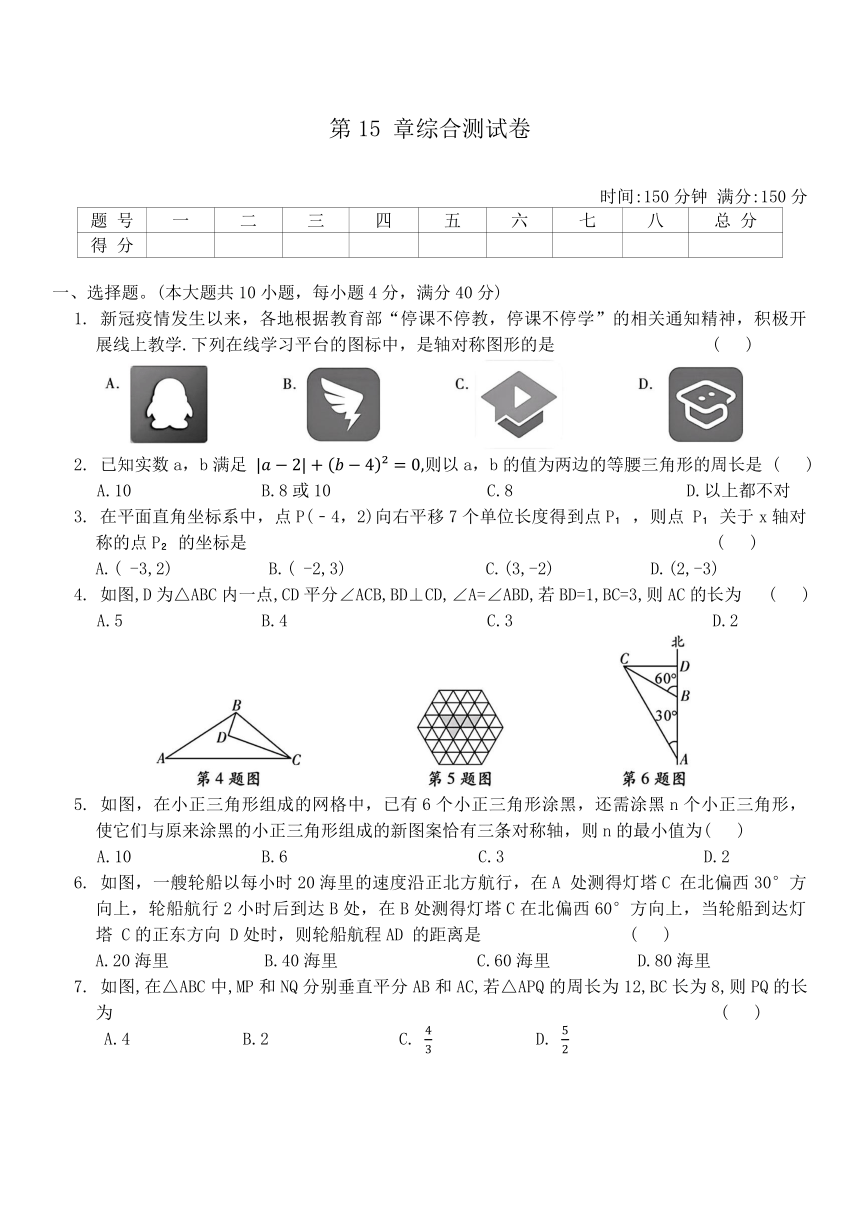
1. 新冠疫情发生以来,各地根据教育部“停课不停教,停课不停学”的相关通知精神,积极开展线上教学.下列在线学习平台的图标中,是轴对称图形的是 ( )
2. 已知实数a,b满足 则以a,b的值为两边的等腰三角形的周长是 ( )
A.10 B.8或10 C.8 D.以上都不对
3. 在平面直角坐标系中,点P(﹣4,2)向右平移7个单位长度得到点P ,则点 P 关于x轴对称的点P 的坐标是 ( )
A.( -3,2) B.( -2,3) C.(3,-2) D.(2,-3)
4. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若BD=1,BC=3,则AC的长为 ( )
A.5 B.4 C.3 D.2
5. 如图,在小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑n个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.10 B.6 C.3 D.2
6. 如图,一艘轮船以每小时20海里的速度沿正北方航行,在A 处测得灯塔C 在北偏西30°方向上,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向上,当轮船到达灯塔 C的正东方向 D处时,则轮船航程AD 的距离是 ( )
A.20海里 B.40海里 C.60海里 D.80海里
7. 如图,在△ABC中,MP和NQ分别垂直平分AB和AC,若△APQ的周长为12,BC长为8,则PQ的长为 ( )
A.4 B.2 C. D.
8. 在线段AB上,分别以点A,B为圆心,以大 AB为半径画弧,两弧分别交于点E、点F,作线EF与AB交于点 C.连接AE,BE,则以下结论不一定成立的是 ( )
A. AC=BC B. AE=BE
C.∠AEC=∠BEC D.△ABE是等边三角形
9. 如图,在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点 F,过点F作EF⊥BC 于点E,则 BE的长为 ( )
A.1 B. C. D.
10. 如图,△ABC中,AD⊥BC交 BC于点 D,AE平分∠BAC交BC于点 E,F 为BC的延长线上一点,FG⊥AE交 AD的延长线于点G,AC的延长线交 FG于点H,连接BG,下列结论:①∠DAE=∠F;②∠DAE (∠ABD-∠ACE);③S△AED:S△AEC =AB:AC;④∠AGH=∠BAE +∠ACB,其中正的结论有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD 恰好平分∠BAC.若DE=1,则BC的长是 .
12. 如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,点M为AB的中点,若∠CMD=120°,则 CD 的最大值是 .
13. 如图,△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于点 D,点E,F 分别在线段BD,CD上,点G在 EF 的延长线上,△EFD与△EFH关于直线EF对称,若∠A=60°,∠BEH=84°,∠HFG=n°,则n= .
14. 如图,△ABC中,AB=AC,∠BAC=48°,∠BAC的平分线与线段AB 的垂直平分线OD交于点O.连接OB,OC,将∠ACB 沿 EF(E 在 BC 上,F 在 AC 上)折叠,点 C 与点 O 恰好重合,则∠OEC 为 度.
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,已知△ABC的顶点分别为A(﹣2,2),B(﹣4,5),C(﹣5,1)和直线m(直线m上各点的横坐标都为1).
(1)作出△ABC关于x轴对称的图形△A B C ,并写出点A 的坐标.
(2)作出点 C关于直线m对称的点 C ,并写出点 C 的坐标.
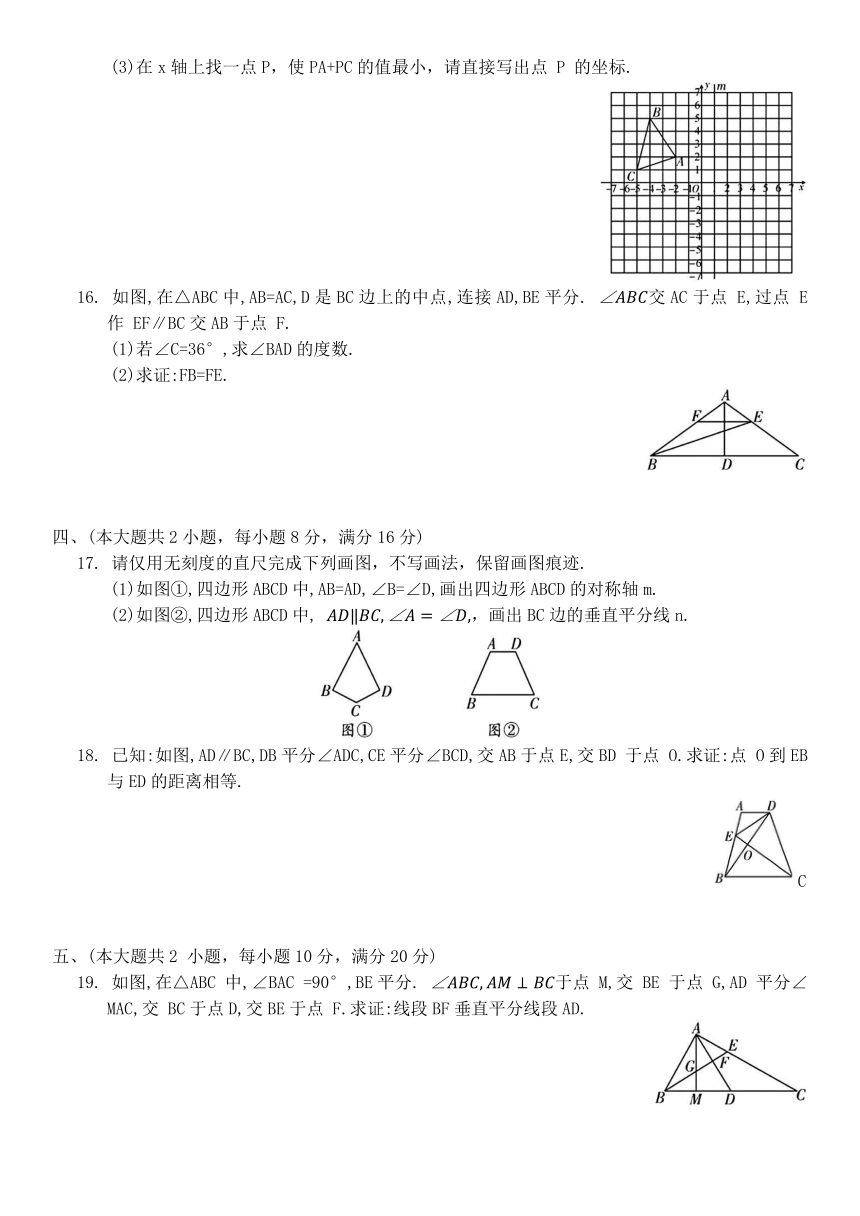
(3)在x轴上找一点P,使PA+PC的值最小,请直接写出点 P 的坐标.
16. 如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分. 交AC于点 E,过点 E 作 EF∥BC交AB于点 F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:FB=FE.
四、(本大题共2小题,每小题8分,满分16分)
17. 请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m.
(2)如图②,四边形ABCD中, ,画出BC边的垂直平分线n.
18. 已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,交BD 于点 O.求证:点 O到EB与ED的距离相等.
C
五、(本大题共2 小题,每小题10分,满分20分)
19. 如图,在△ABC 中,∠BAC =90°,BE平分. 于点 M,交 BE 于点 G,AD 平分∠MAC,交 BC于点D,交BE于点 F.求证:线段BF垂直平分线段AD.
20. 如图,点 P 为△ABC三边垂直平分线的交点,
(1)求∠PAB的度数.
(2)直接写出∠APB 与∠ACB的数量关系 .
六、(本题满分12分)
21. 如图,△ABC中,AD平分∠BAC,DG⊥BC且平分 BC,DE⊥AB于点E, 于点F.
(1)证明:BE=CF.
(2)如果AB=5,AC=3,求AE,BE的长.
七、(本题满分12分)
22. 已知:如图,AF平分∠BAC,BC垂直平分AD,垂足为E,P为边CF 上一点,连接PB交线段AF相交于点M.
(1)求证:AB∥CD.
(2)若∠DAC=∠MPC,请你判断∠F 与∠MCD的数量关系,并说明理由.
八、(本题满分14分)
23. 在平面直角坐标系xOy中,点A在x轴的正半轴上运动,点B在y轴的正半轴上运动, 的外角平分线相交于点C,如图1所示,连接CO.
(1)求证:CO平分.
(2)延长CB交∠BAO的平分线于点 D,如图2所示,求证:
第15 章综合测试卷
1. A 2. A 3. C 4. A 5. C 6. C 7. B 8. D 9. C 10. D11.3 12.14 13.78 14.96
15.解:(1)如图所示, 即为所求,其中点 的坐标为( -2,-2).
(2)点 C 如图所示,C (7,1).
(3)如图所示,点P为所求,
16.(1)解:∵
(2)证明:∵ BE平分 ∵EF∥BC,∴∠FEB=∠CBE,
∴∠FBE=∠FEB,∴FB=FE.
17.解:(1)如图①,直线m即为所求.
(2)如图②,直线 n 即为所求.
18.证明:∵AD∥BC,∴∠ADC+∠BCD=180°,
∵ DB平分∠ADC,CE平分∠BCD,
∴∠ODC+∠OCD=90°,∴∠DOC=90°,
又∵CE平分∠BCD,∴CB=CD,∴OB=OD,
∴CE是BD的垂直平分线,∴EB=ED,
又∵∠DOC=90°,∴EC平分∠BED,
∴点O到EB 与ED的距离相等.
19.证明:∵∠BAC=90°,∴∠ABC+∠C=90°,
∵AM⊥BC,∴∠AMB=90°,
∴∠ABC+∠BAM=90°,∴∠C=∠BAM,
∵AD平分∠MAC,∴∠MAD=∠CAD,
∴∠BAM+∠MAD=∠C+∠CAD,
∵ ∠ADB=∠C+∠CAD,
∴∠BAD=∠ADB,∴AB=BD,
又∵BE平分∠ABC,∴BF⊥AD,AF=FD,
即线段 BF垂直平分线段AD.
20.解:(1)∵P为△ABC三边垂直平分线的交点,
∴PA=PC=PB,
∴∠PAC=∠PCA=20°,∠PBC=∠PCB=30°,
∵ ∠PAB=∠PBA,
∴∠APB=2∠ACB.
故答案为:∠APB=2∠ACB.
21.(1)证明:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵ DG⊥BC且平分BC,∴BD=CD,在 Rt△BED与Rt△CFD中,∴Rt△BED≌Rt△CFD(HL),∴BE=CF.
(2)解:在△AED和△AFD中,
∴△AED≌△AFD(AAS),∴AE=AF,设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB-BE,AF=AC+CF,
∴5-x=3+x,解得x=1,
∴BE=1,AE=AB-BE=5-1=4.
22.解:(1)∵BC垂直平分AD,
∴AC=CD,∴∠CAD=∠CDA,
∵AF平分∠BAC,∴∠CAD=∠BAD,
∴∠CDA=∠BAD,∴AB∥CD.
(2)∠F=∠MCD,
理由如下:∵∠DAC=∠CDA,∠DAC=∠MPC,
∴∠CDA=∠MPC,
又∵∠CDA+∠CDM=180°,∠MPC+∠MPF=180°,
∴∠CDM=∠MPF,
∵AF平分∠BAC,AE⊥BC,AE=AE.
∵AF 平分
∴△ACM≌△ABM(SAS),∴∠AMC=∠AMB,
又∵∠AMB=∠PMF.∴∠AMC=∠PMF.
又∵
∠PMF+∠MPF+∠F=180°,∴∠F=∠MCD.
23.证明:(1)过C分别向x轴,y轴,AB 作垂线,垂足为H ,H ,H ,
∵ BC 平分
∵ AC平分.
∴CO平分∠AOB.
(2)作射线AE,∵ BC为角平分线,∴∠OBE=2∠DBE.
∵AD平分∠BAO,∴∠BAO=2∠BAD.
∵∠OBE=∠AOB+∠BAO,∠DBE=∠BAD+∠D,∠OBE=2∠DBE,∠BAO=2∠BAD,
又∴
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题。(本大题共10小题,每小题4分,满分40分)
1. 新冠疫情发生以来,各地根据教育部“停课不停教,停课不停学”的相关通知精神,积极开展线上教学.下列在线学习平台的图标中,是轴对称图形的是 ( )
2. 已知实数a,b满足 则以a,b的值为两边的等腰三角形的周长是 ( )
A.10 B.8或10 C.8 D.以上都不对
3. 在平面直角坐标系中,点P(﹣4,2)向右平移7个单位长度得到点P ,则点 P 关于x轴对称的点P 的坐标是 ( )
A.( -3,2) B.( -2,3) C.(3,-2) D.(2,-3)
4. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若BD=1,BC=3,则AC的长为 ( )
A.5 B.4 C.3 D.2
5. 如图,在小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑n个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.10 B.6 C.3 D.2
6. 如图,一艘轮船以每小时20海里的速度沿正北方航行,在A 处测得灯塔C 在北偏西30°方向上,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向上,当轮船到达灯塔 C的正东方向 D处时,则轮船航程AD 的距离是 ( )
A.20海里 B.40海里 C.60海里 D.80海里
7. 如图,在△ABC中,MP和NQ分别垂直平分AB和AC,若△APQ的周长为12,BC长为8,则PQ的长为 ( )
A.4 B.2 C. D.
8. 在线段AB上,分别以点A,B为圆心,以大 AB为半径画弧,两弧分别交于点E、点F,作线EF与AB交于点 C.连接AE,BE,则以下结论不一定成立的是 ( )
A. AC=BC B. AE=BE
C.∠AEC=∠BEC D.△ABE是等边三角形
9. 如图,在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点 F,过点F作EF⊥BC 于点E,则 BE的长为 ( )
A.1 B. C. D.
10. 如图,△ABC中,AD⊥BC交 BC于点 D,AE平分∠BAC交BC于点 E,F 为BC的延长线上一点,FG⊥AE交 AD的延长线于点G,AC的延长线交 FG于点H,连接BG,下列结论:①∠DAE=∠F;②∠DAE (∠ABD-∠ACE);③S△AED:S△AEC =AB:AC;④∠AGH=∠BAE +∠ACB,其中正的结论有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD 恰好平分∠BAC.若DE=1,则BC的长是 .
12. 如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,点M为AB的中点,若∠CMD=120°,则 CD 的最大值是 .
13. 如图,△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于点 D,点E,F 分别在线段BD,CD上,点G在 EF 的延长线上,△EFD与△EFH关于直线EF对称,若∠A=60°,∠BEH=84°,∠HFG=n°,则n= .
14. 如图,△ABC中,AB=AC,∠BAC=48°,∠BAC的平分线与线段AB 的垂直平分线OD交于点O.连接OB,OC,将∠ACB 沿 EF(E 在 BC 上,F 在 AC 上)折叠,点 C 与点 O 恰好重合,则∠OEC 为 度.
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,已知△ABC的顶点分别为A(﹣2,2),B(﹣4,5),C(﹣5,1)和直线m(直线m上各点的横坐标都为1).
(1)作出△ABC关于x轴对称的图形△A B C ,并写出点A 的坐标.
(2)作出点 C关于直线m对称的点 C ,并写出点 C 的坐标.
(3)在x轴上找一点P,使PA+PC的值最小,请直接写出点 P 的坐标.
16. 如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分. 交AC于点 E,过点 E 作 EF∥BC交AB于点 F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:FB=FE.
四、(本大题共2小题,每小题8分,满分16分)
17. 请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m.
(2)如图②,四边形ABCD中, ,画出BC边的垂直平分线n.
18. 已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,交BD 于点 O.求证:点 O到EB与ED的距离相等.
C
五、(本大题共2 小题,每小题10分,满分20分)
19. 如图,在△ABC 中,∠BAC =90°,BE平分. 于点 M,交 BE 于点 G,AD 平分∠MAC,交 BC于点D,交BE于点 F.求证:线段BF垂直平分线段AD.
20. 如图,点 P 为△ABC三边垂直平分线的交点,
(1)求∠PAB的度数.
(2)直接写出∠APB 与∠ACB的数量关系 .
六、(本题满分12分)
21. 如图,△ABC中,AD平分∠BAC,DG⊥BC且平分 BC,DE⊥AB于点E, 于点F.
(1)证明:BE=CF.
(2)如果AB=5,AC=3,求AE,BE的长.
七、(本题满分12分)
22. 已知:如图,AF平分∠BAC,BC垂直平分AD,垂足为E,P为边CF 上一点,连接PB交线段AF相交于点M.
(1)求证:AB∥CD.
(2)若∠DAC=∠MPC,请你判断∠F 与∠MCD的数量关系,并说明理由.
八、(本题满分14分)
23. 在平面直角坐标系xOy中,点A在x轴的正半轴上运动,点B在y轴的正半轴上运动, 的外角平分线相交于点C,如图1所示,连接CO.
(1)求证:CO平分.
(2)延长CB交∠BAO的平分线于点 D,如图2所示,求证:
第15 章综合测试卷
1. A 2. A 3. C 4. A 5. C 6. C 7. B 8. D 9. C 10. D11.3 12.14 13.78 14.96
15.解:(1)如图所示, 即为所求,其中点 的坐标为( -2,-2).
(2)点 C 如图所示,C (7,1).
(3)如图所示,点P为所求,
16.(1)解:∵
(2)证明:∵ BE平分 ∵EF∥BC,∴∠FEB=∠CBE,
∴∠FBE=∠FEB,∴FB=FE.
17.解:(1)如图①,直线m即为所求.
(2)如图②,直线 n 即为所求.
18.证明:∵AD∥BC,∴∠ADC+∠BCD=180°,
∵ DB平分∠ADC,CE平分∠BCD,
∴∠ODC+∠OCD=90°,∴∠DOC=90°,
又∵CE平分∠BCD,∴CB=CD,∴OB=OD,
∴CE是BD的垂直平分线,∴EB=ED,
又∵∠DOC=90°,∴EC平分∠BED,
∴点O到EB 与ED的距离相等.
19.证明:∵∠BAC=90°,∴∠ABC+∠C=90°,
∵AM⊥BC,∴∠AMB=90°,
∴∠ABC+∠BAM=90°,∴∠C=∠BAM,
∵AD平分∠MAC,∴∠MAD=∠CAD,
∴∠BAM+∠MAD=∠C+∠CAD,
∵ ∠ADB=∠C+∠CAD,
∴∠BAD=∠ADB,∴AB=BD,
又∵BE平分∠ABC,∴BF⊥AD,AF=FD,
即线段 BF垂直平分线段AD.
20.解:(1)∵P为△ABC三边垂直平分线的交点,
∴PA=PC=PB,
∴∠PAC=∠PCA=20°,∠PBC=∠PCB=30°,
∵ ∠PAB=∠PBA,
∴∠APB=2∠ACB.
故答案为:∠APB=2∠ACB.
21.(1)证明:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵ DG⊥BC且平分BC,∴BD=CD,在 Rt△BED与Rt△CFD中,∴Rt△BED≌Rt△CFD(HL),∴BE=CF.
(2)解:在△AED和△AFD中,
∴△AED≌△AFD(AAS),∴AE=AF,设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB-BE,AF=AC+CF,
∴5-x=3+x,解得x=1,
∴BE=1,AE=AB-BE=5-1=4.
22.解:(1)∵BC垂直平分AD,
∴AC=CD,∴∠CAD=∠CDA,
∵AF平分∠BAC,∴∠CAD=∠BAD,
∴∠CDA=∠BAD,∴AB∥CD.
(2)∠F=∠MCD,
理由如下:∵∠DAC=∠CDA,∠DAC=∠MPC,
∴∠CDA=∠MPC,
又∵∠CDA+∠CDM=180°,∠MPC+∠MPF=180°,
∴∠CDM=∠MPF,
∵AF平分∠BAC,AE⊥BC,AE=AE.
∵AF 平分
∴△ACM≌△ABM(SAS),∴∠AMC=∠AMB,
又∵∠AMB=∠PMF.∴∠AMC=∠PMF.
又∵
∠PMF+∠MPF+∠F=180°,∴∠F=∠MCD.
23.证明:(1)过C分别向x轴,y轴,AB 作垂线,垂足为H ,H ,H ,
∵ BC 平分
∵ AC平分.
∴CO平分∠AOB.
(2)作射线AE,∵ BC为角平分线,∴∠OBE=2∠DBE.
∵AD平分∠BAO,∴∠BAO=2∠BAD.
∵∠OBE=∠AOB+∠BAO,∠DBE=∠BAD+∠D,∠OBE=2∠DBE,∠BAO=2∠BAD,
又∴
