沪科版数学八年级上册 专项练习 (一)平面直角坐标系 一次函数(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 专项练习 (一)平面直角坐标系 一次函数(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 793.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 00:00:00 | ||
图片预览



文档简介
专项练习 (一)平面直角坐标系 一次函数
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题5分,满分50分)
1. 若a+b=0,则点P(a,b)一定不在 ( )
A.坐标轴上 B.第四象限 C.第二象限 D.第一象限
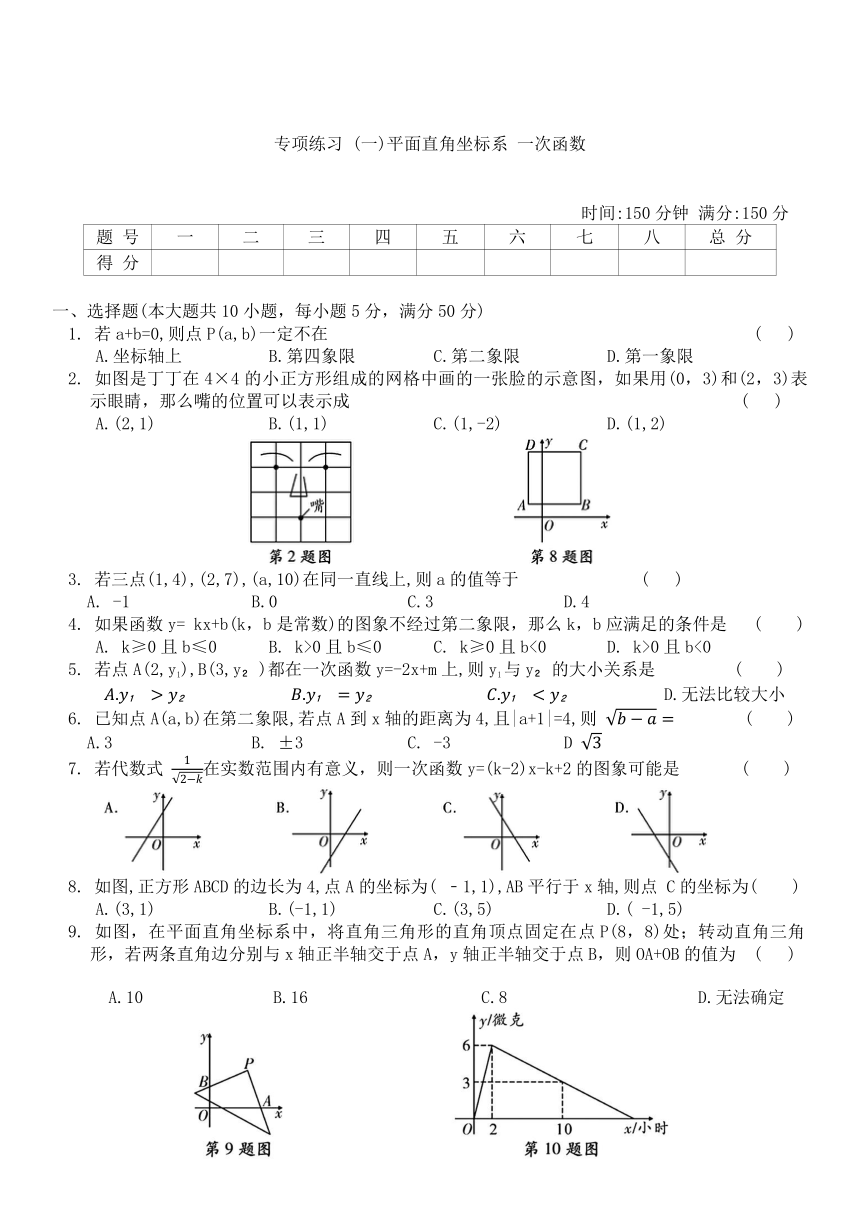
2. 如图是丁丁在4×4的小正方形组成的网格中画的一张脸的示意图,如果用(0,3)和(2,3)表示眼睛,那么嘴的位置可以表示成 ( )
A.(2,1) B.(1,1) C.(1,-2) D.(1,2)
3. 若三点(1,4),(2,7),(a,10)在同一直线上,则a的值等于 ( )
A. -1 B.0 C.3 D.4
4. 如果函数y= kx+b(k,b是常数)的图象不经过第二象限,那么k,b应满足的条件是 ( )
A. k≥0且b≤0 B. k>0且b≤0 C. k≥0且b<0 D. k>0且b<0
5. 若点A(2,y1),B(3,y )都在一次函数y=-2x+m上,则y1与y 的大小关系是 ( )
D.无法比较大小
6. 已知点A(a,b)在第二象限,若点A到x轴的距离为4,且|a+1|=4,则 ( )
A.3 B. ±3 C. -3 D
7. 若代数式 在实数范围内有意义,则一次函数y=(k-2)x-k+2的图象可能是 ( )
8. 如图,正方形ABCD的边长为4,点A的坐标为( ﹣1,1),AB平行于x轴,则点 C的坐标为( )
A.(3,1) B.(-1,1) C.(3,5) D.( -1,5)
9. 如图,在平面直角坐标系中,将直角三角形的直角顶点固定在点P(8,8)处;转动直角三角形,若两条直角边分别与x轴正半轴交于点A,y轴正半轴交于点B,则OA+OB的值为 ( )
A.10 B.16 C.8 D.无法确定
10. 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2 小时血液中含药量最高,达每毫升6微克(1微克=10 毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,如果每毫升血液中含药量为5微克或5微克以上,对于治疗疾病是有效的,那么该药治疗的有效时长是 ( )
A.6小时 B.3小时 C. 小时 D. 小时
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 在平面直角坐标系中,有一条线段AB.已知点A(-3,0)和B(0,4),平移线段AB得到线段 A1B1,若点A的对应点 A1的坐标为(0,-1),则线段AB平移经过的区域(四边形ABB1A1)的面积为 .
12. 已知整数a使得不等式组 的解集为x>-4,且使得一次函数y=(a+5)x+5的图象不经过第四象限,则整数a的值为 .
13. 某市政府大力扶持大学生创业.小甬在政府的扶持下投资销售一种进价为每件20 元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数:y=-10x+500.根据物价部门规定,这种护眼台灯的销售单价不得高于32元,那么他每月的成本最少需要 元.(成本=进价×销售量)
14. 如图,在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点称为“整点”,已知点A的坐标为(5,0),点B在x轴的上方,△OAB的面积为 则△OAB内部(不含边界)的整点的个数为 .
三、(本大题共2小题,每小题8分,满分16分)
15. 平面直角坐标系中,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为:「P」,即「P」=|x|+|y|.
(1)求点A(﹣1,3)的勾股值「A」.
(2)若点 B在第一象限且满足「B」=3,求满足条件的所有点 B 与坐标轴围成的图形的面积.
16. 已知点M(3a-2,a+6),分别根据下列条件求出点M的坐标.
(1)点M在x轴上.
(2)点N的坐标为(2,5),且直线MN∥x轴.
(3)点M到x轴、y轴的距离相等.
四、(本大题共2小题,每小题8分,满分16分)
17. 已知直线 与直线 交于点A(2,4),直线 与x轴交于点 B,直线 与y轴交于点C.
(1)求m,n的值.
(2)画出图象,写出当x为何值时,
(3)求△ABC的面积.
18. 在平面直角坐标系中,对于点 P(x,y),若点 Q的坐标为( ,其中a为常数,则称点Q 是点P的“a级关联点”.例如,点P(1,4)的“3级关联点”为 即Q(7,13).
(1)已知点A(-2,6)的 级关联点”是点 A1,求点 A1的坐标.
(2)已知点M(m-1,2m)的“-3级关联点”M'位于y轴上,求点 的坐标.
五、(本题满分10分)
19. 如图,已知O为坐标原点直线 的图象经过点 且与直线 交于点B(1,b).
(1)求直线l1 的解析式,并直接写出不等式. 的解集.
(2)若直线l1与x轴交于点C,在x轴上是否存在一点 P,满足 若存在,求出此时点P 的坐标;若不存在,请说明理由.
六、(本题满分12分)
20. 如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系 乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图2所示:
(1)求y关于x的函数表达式.
(2)请通过计算说明甲、乙两人谁先到达一楼地面.
七、(本题满分12 分)
21. 如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点 C,点D 在第一象限,直线AC交x轴于点 F.
(1)线段 CD 由线段AB 经过怎样平移得到
(2)点D坐标为 .
(3)求△BCF的面积.
八、(本题满分 14 分)
22. 为了抗击新冠病毒疫情,全国人民众志成城,守望相助,春节后某地一水果购销商安排15 辆汽车装运A,B,C三种水果120 吨销售,所得利润全部捐赠湖北抗疫,已知按计划15 辆汽车都要装满且每辆汽车只能装同一种水果,每种水果所用车辆均不少于3辆,汽车对不同水果的运载量和每吨水果销售获利情况如下表:
水果品种 A B C
汽车运载量(吨/辆) 10 8 6
水果获利(元/吨) 800 1 200 1 000
(1)设装运A种水果的车辆数为x辆,装运B种水果的车辆数为y辆,根据上表提供的信息,
①求y与x之间的函数关系式.
②设计车辆的安排方案,并写出每种安排方案.
(2)若原有获利不变的情况下,当地政府按每吨50元的标准实行运费补贴,该经销商打算将获利连同补贴全部捐出,问应采用哪种车辆安排方案,可以使这次捐款数w(元)最大化 捐款数w(元)最大是多少
专项练习(一)
D 2. B 3. C 4. A 5. A 6. A 7. C 8. C 9. B 10. B11.15 12. -4 13.3600
14.4或5或6
15.解:(1)「A」=1-1|+|3|=4.
(2)设B(x,y),由「B」=3且在第一象限知,x+y=3(x>0,y>0),
即y=-x+3(x>0,y>0).
故所有点 B与坐标轴围成的图形为如图所示的三角形,
其面积为
16.解:(1)∵点M在x轴上,∴a+6=0,
解得a=-6,则3a-2=-18-2=-20,
∴点M的坐标为( -20,0).
(2)∵直线MN∥x轴,∴a+6=5,解得a=-1,
则3a-2=3×(-1)-2=-5,∴点M的坐标为( -5,5).
(3)∵点M到x轴、y轴的距离相等,
∴3a-2=a+6,或3a-2+a+6=0,
解得a=4,或a=-1,
则3a-2=3×4-2=10,或3a-2=3×(-1)-2=-5,
∴点M的坐标为(10, 10)或( -5,5).
17.解:(1)把A(2,4)代入 得2m-4=4,解得m=4.
把A(2,4)代入 ,得-2+n=4,解得n=6.
(2)如图所示,当x>2时, 当x<2时,
(3)直线 与x轴的交点B的坐标为(1,0),与y轴的交点D的坐标为(0,-4).
直线 与y轴的交点C的坐标为(0,6),
18.解:(1)∵点A( -2,6)的 级关联点”是点A1,∴点 的坐标为( -2 即
(2)∵点M(m-1,2m)的“-3级关联点”为M',∴M'的坐标为(-m+3,-5m-1),又∵M'位于y轴上.
∴--m+3=0,解得m=3,∴ -5m-1=-16,∴M'(0,-16).
19.解:(1)把B(1,b)代入 得b=3,则B(1,3);把A( -2,6),B(1,3)代入 得 解得所以直线 的解析式为 不等式 的解集为x≤1.
(2)存在.当y=0时, 解得x=4,则C(4,0),设P(t,0), 解得t=10或t= -2,
∴P点坐标为( -2,0),(10,0).
20.解:(1)设y关于x的函数表达式为 ,把点(15,3),(0,6)代入,
得解得
∴y关于x的函数表达式是
当h=0时, 解得 当y=0时,
解得 ∵20<30,∴甲先到达一楼地面.
21.解:(1)线段CD是由线段AB向右平移5个单位,再向上平移3个单位得到.
(2)由(1)知点A(0,5)向右平移5个单位,再向上平移3个单位得到点D(5,8).
(3)过点 C作CF⊥x轴于 H,设直线AC的表达式为y= kx+b,
把A(0,5),C(3,3)代入,得 解得
∴直线 AC 的表达式为
∴ 点 F 的坐标为
22.解:(1)①设装运A种水果的车辆数为x辆,装运B种水果车辆数为y辆,则装C种水果的车辆是(15-x-y)辆.
由题意,得10x+8y+6(15-x-y)=120,
即y=15-2x.
②根据题意得
解得3≤x≤6.
∵x为整数,∴x可取3,4,5,6.
即共有四种方案:装运A、B、C三种水果的车辆数分别是:3辆、9辆、3辆;或4辆、7辆、4辆;或5辆、5辆、5辆;或6辆、3辆、6辆.
由题意,得:
w=800×10x+1200×8(15-2x)+1000×6[15-x- (15
∵ -5200<0,∴w随x的增大而减小.
当x=3时,w有最大值,是 (元).
答:采用装运A、B、C三种水果的车辆数分别是:3辆、9辆、3辆的方案,捐款数w最大为134400 元.
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题5分,满分50分)
1. 若a+b=0,则点P(a,b)一定不在 ( )
A.坐标轴上 B.第四象限 C.第二象限 D.第一象限
2. 如图是丁丁在4×4的小正方形组成的网格中画的一张脸的示意图,如果用(0,3)和(2,3)表示眼睛,那么嘴的位置可以表示成 ( )
A.(2,1) B.(1,1) C.(1,-2) D.(1,2)
3. 若三点(1,4),(2,7),(a,10)在同一直线上,则a的值等于 ( )
A. -1 B.0 C.3 D.4
4. 如果函数y= kx+b(k,b是常数)的图象不经过第二象限,那么k,b应满足的条件是 ( )
A. k≥0且b≤0 B. k>0且b≤0 C. k≥0且b<0 D. k>0且b<0
5. 若点A(2,y1),B(3,y )都在一次函数y=-2x+m上,则y1与y 的大小关系是 ( )
D.无法比较大小
6. 已知点A(a,b)在第二象限,若点A到x轴的距离为4,且|a+1|=4,则 ( )
A.3 B. ±3 C. -3 D
7. 若代数式 在实数范围内有意义,则一次函数y=(k-2)x-k+2的图象可能是 ( )
8. 如图,正方形ABCD的边长为4,点A的坐标为( ﹣1,1),AB平行于x轴,则点 C的坐标为( )
A.(3,1) B.(-1,1) C.(3,5) D.( -1,5)
9. 如图,在平面直角坐标系中,将直角三角形的直角顶点固定在点P(8,8)处;转动直角三角形,若两条直角边分别与x轴正半轴交于点A,y轴正半轴交于点B,则OA+OB的值为 ( )
A.10 B.16 C.8 D.无法确定
10. 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2 小时血液中含药量最高,达每毫升6微克(1微克=10 毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,如果每毫升血液中含药量为5微克或5微克以上,对于治疗疾病是有效的,那么该药治疗的有效时长是 ( )
A.6小时 B.3小时 C. 小时 D. 小时
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 在平面直角坐标系中,有一条线段AB.已知点A(-3,0)和B(0,4),平移线段AB得到线段 A1B1,若点A的对应点 A1的坐标为(0,-1),则线段AB平移经过的区域(四边形ABB1A1)的面积为 .
12. 已知整数a使得不等式组 的解集为x>-4,且使得一次函数y=(a+5)x+5的图象不经过第四象限,则整数a的值为 .
13. 某市政府大力扶持大学生创业.小甬在政府的扶持下投资销售一种进价为每件20 元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数:y=-10x+500.根据物价部门规定,这种护眼台灯的销售单价不得高于32元,那么他每月的成本最少需要 元.(成本=进价×销售量)
14. 如图,在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点称为“整点”,已知点A的坐标为(5,0),点B在x轴的上方,△OAB的面积为 则△OAB内部(不含边界)的整点的个数为 .
三、(本大题共2小题,每小题8分,满分16分)
15. 平面直角坐标系中,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为:「P」,即「P」=|x|+|y|.
(1)求点A(﹣1,3)的勾股值「A」.
(2)若点 B在第一象限且满足「B」=3,求满足条件的所有点 B 与坐标轴围成的图形的面积.
16. 已知点M(3a-2,a+6),分别根据下列条件求出点M的坐标.
(1)点M在x轴上.
(2)点N的坐标为(2,5),且直线MN∥x轴.
(3)点M到x轴、y轴的距离相等.
四、(本大题共2小题,每小题8分,满分16分)
17. 已知直线 与直线 交于点A(2,4),直线 与x轴交于点 B,直线 与y轴交于点C.
(1)求m,n的值.
(2)画出图象,写出当x为何值时,
(3)求△ABC的面积.
18. 在平面直角坐标系中,对于点 P(x,y),若点 Q的坐标为( ,其中a为常数,则称点Q 是点P的“a级关联点”.例如,点P(1,4)的“3级关联点”为 即Q(7,13).
(1)已知点A(-2,6)的 级关联点”是点 A1,求点 A1的坐标.
(2)已知点M(m-1,2m)的“-3级关联点”M'位于y轴上,求点 的坐标.
五、(本题满分10分)
19. 如图,已知O为坐标原点直线 的图象经过点 且与直线 交于点B(1,b).
(1)求直线l1 的解析式,并直接写出不等式. 的解集.
(2)若直线l1与x轴交于点C,在x轴上是否存在一点 P,满足 若存在,求出此时点P 的坐标;若不存在,请说明理由.
六、(本题满分12分)
20. 如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系 乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图2所示:
(1)求y关于x的函数表达式.
(2)请通过计算说明甲、乙两人谁先到达一楼地面.
七、(本题满分12 分)
21. 如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点 C,点D 在第一象限,直线AC交x轴于点 F.
(1)线段 CD 由线段AB 经过怎样平移得到
(2)点D坐标为 .
(3)求△BCF的面积.
八、(本题满分 14 分)
22. 为了抗击新冠病毒疫情,全国人民众志成城,守望相助,春节后某地一水果购销商安排15 辆汽车装运A,B,C三种水果120 吨销售,所得利润全部捐赠湖北抗疫,已知按计划15 辆汽车都要装满且每辆汽车只能装同一种水果,每种水果所用车辆均不少于3辆,汽车对不同水果的运载量和每吨水果销售获利情况如下表:
水果品种 A B C
汽车运载量(吨/辆) 10 8 6
水果获利(元/吨) 800 1 200 1 000
(1)设装运A种水果的车辆数为x辆,装运B种水果的车辆数为y辆,根据上表提供的信息,
①求y与x之间的函数关系式.
②设计车辆的安排方案,并写出每种安排方案.
(2)若原有获利不变的情况下,当地政府按每吨50元的标准实行运费补贴,该经销商打算将获利连同补贴全部捐出,问应采用哪种车辆安排方案,可以使这次捐款数w(元)最大化 捐款数w(元)最大是多少
专项练习(一)
D 2. B 3. C 4. A 5. A 6. A 7. C 8. C 9. B 10. B11.15 12. -4 13.3600
14.4或5或6
15.解:(1)「A」=1-1|+|3|=4.
(2)设B(x,y),由「B」=3且在第一象限知,x+y=3(x>0,y>0),
即y=-x+3(x>0,y>0).
故所有点 B与坐标轴围成的图形为如图所示的三角形,
其面积为
16.解:(1)∵点M在x轴上,∴a+6=0,
解得a=-6,则3a-2=-18-2=-20,
∴点M的坐标为( -20,0).
(2)∵直线MN∥x轴,∴a+6=5,解得a=-1,
则3a-2=3×(-1)-2=-5,∴点M的坐标为( -5,5).
(3)∵点M到x轴、y轴的距离相等,
∴3a-2=a+6,或3a-2+a+6=0,
解得a=4,或a=-1,
则3a-2=3×4-2=10,或3a-2=3×(-1)-2=-5,
∴点M的坐标为(10, 10)或( -5,5).
17.解:(1)把A(2,4)代入 得2m-4=4,解得m=4.
把A(2,4)代入 ,得-2+n=4,解得n=6.
(2)如图所示,当x>2时, 当x<2时,
(3)直线 与x轴的交点B的坐标为(1,0),与y轴的交点D的坐标为(0,-4).
直线 与y轴的交点C的坐标为(0,6),
18.解:(1)∵点A( -2,6)的 级关联点”是点A1,∴点 的坐标为( -2 即
(2)∵点M(m-1,2m)的“-3级关联点”为M',∴M'的坐标为(-m+3,-5m-1),又∵M'位于y轴上.
∴--m+3=0,解得m=3,∴ -5m-1=-16,∴M'(0,-16).
19.解:(1)把B(1,b)代入 得b=3,则B(1,3);把A( -2,6),B(1,3)代入 得 解得所以直线 的解析式为 不等式 的解集为x≤1.
(2)存在.当y=0时, 解得x=4,则C(4,0),设P(t,0), 解得t=10或t= -2,
∴P点坐标为( -2,0),(10,0).
20.解:(1)设y关于x的函数表达式为 ,把点(15,3),(0,6)代入,
得解得
∴y关于x的函数表达式是
当h=0时, 解得 当y=0时,
解得 ∵20<30,∴甲先到达一楼地面.
21.解:(1)线段CD是由线段AB向右平移5个单位,再向上平移3个单位得到.
(2)由(1)知点A(0,5)向右平移5个单位,再向上平移3个单位得到点D(5,8).
(3)过点 C作CF⊥x轴于 H,设直线AC的表达式为y= kx+b,
把A(0,5),C(3,3)代入,得 解得
∴直线 AC 的表达式为
∴ 点 F 的坐标为
22.解:(1)①设装运A种水果的车辆数为x辆,装运B种水果车辆数为y辆,则装C种水果的车辆是(15-x-y)辆.
由题意,得10x+8y+6(15-x-y)=120,
即y=15-2x.
②根据题意得
解得3≤x≤6.
∵x为整数,∴x可取3,4,5,6.
即共有四种方案:装运A、B、C三种水果的车辆数分别是:3辆、9辆、3辆;或4辆、7辆、4辆;或5辆、5辆、5辆;或6辆、3辆、6辆.
由题意,得:
w=800×10x+1200×8(15-2x)+1000×6[15-x- (15
∵ -5200<0,∴w随x的增大而减小.
当x=3时,w有最大值,是 (元).
答:采用装运A、B、C三种水果的车辆数分别是:3辆、9辆、3辆的方案,捐款数w最大为134400 元.
