沪科版数学八年级上册 专项练习 二 三角形中的边角关系、命题与证明 全等三角形(含答案)
文档属性
| 名称 | 沪科版数学八年级上册 专项练习 二 三角形中的边角关系、命题与证明 全等三角形(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 689.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 00:00:00 | ||
图片预览



文档简介
专项练习(二)三角形中的边角关系、命题与证明 全等三角形
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 下列命题中是假命题的是 ( )
A.对顶角相等 B.同旁内角互补 C.两点确定一条直线 D.垂线段最短
2. 下列图形中,具有稳定性的是 ( )
3. 已知△ABC的三边长分别为a,b,c,且M=(a+b+c)(a+b-c)(a-b-c),那么 ( )
A. M>0 B. M≥0 C. M=0 D. M<0
4. 已知△ABC≌△A1B1C1,A和A1对应,B和B1对应,∠A=70°,∠B1=50°,则∠C的度数为 ( )
A.70° B.50° C.120° D.60°
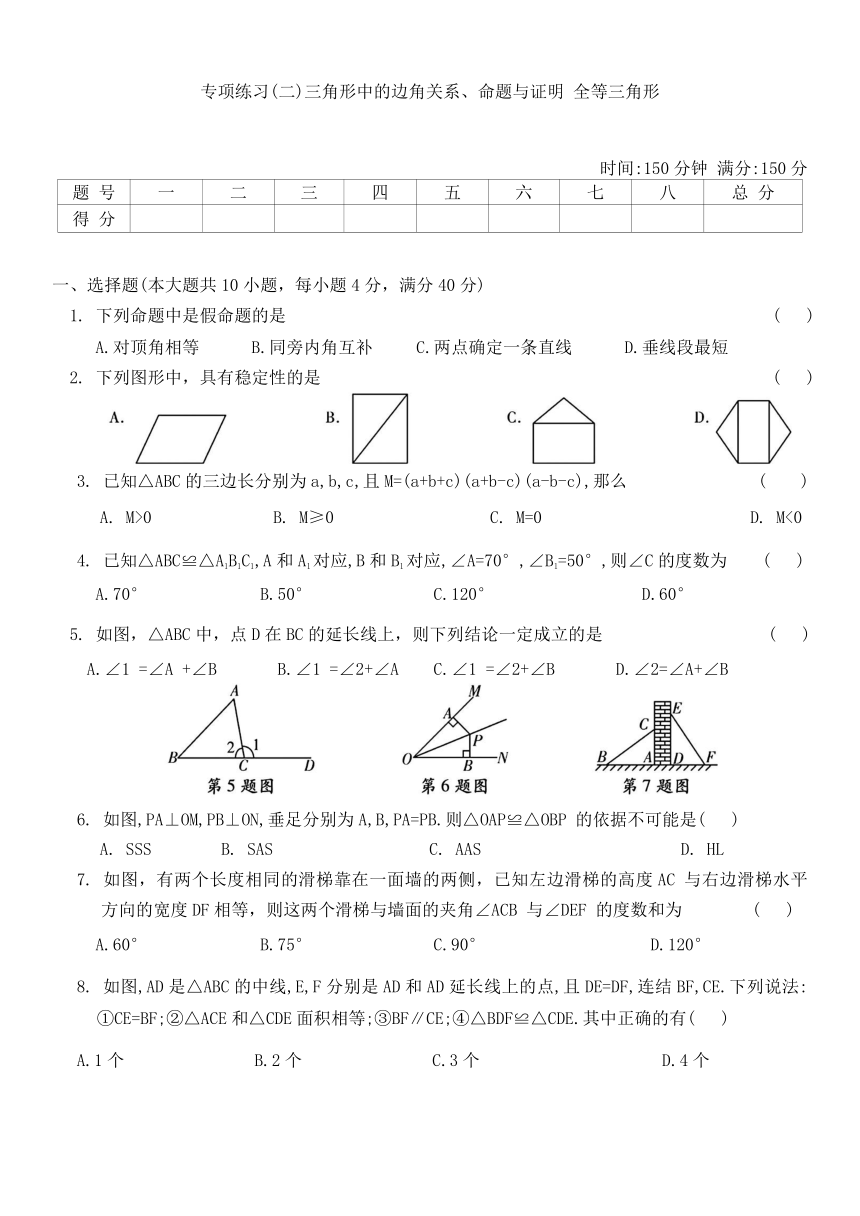
5. 如图,△ABC中,点D在BC的延长线上,则下列结论一定成立的是 ( )
A.∠1 =∠A +∠B B.∠1 =∠2+∠A C.∠1 =∠2+∠B D.∠2=∠A+∠B
6. 如图,PA⊥OM,PB⊥ON,垂足分别为A,B,PA=PB.则△OAP≌△OBP 的依据不可能是( )
A. SSS B. SAS C. AAS D. HL
7. 如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC 与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB 与∠DEF 的度数和为 ( )
A.60° B.75° C.90° D.120°
如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①CE=BF;②△ACE和△CDE面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9. 如图,在△ABC和△A'B'C中,△ABC≌△A'B'C,AA'∥BC,∠ACB=α,∠BCB'=β,则α,β满足关系 ( )
A.α+β=90° B.α+2β=180° C.2α+β=180° D.α+β=180°
10. 如图,已知E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,添加以下条件之一,仍不能证明△ABC≌△DEF的是 ( )
A.∠E=∠ABC B. AB=DE C. AB∥DE D. DF∥AC
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 为说明命题“如果a>b,那么 是假命题,你举出的一个反例是
12. 如图,BA⊥AC,CD∥AB,BC=DE,且BC⊥DE,若AB=5,CD=8,则AE= .
13. 7 条长度均为整数的线段a1,a ,a ,a ,a ,a ,a 满足 且这7条线段中的任意3条都不能构成三角形.若 厘米,a =21厘米,则a 的值是 .
14. 如图,在等腰△ABC中,AB=AC,∠A=20°. AB上一点D,使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE= °.
三、(本大题共2小题,每小题8分,满分16分)
15. (广州中考)如图,D 是AB 上一点,DF 交 AC 于点 E,DE =FE,FC∥AB,求证:△ADE≌△CFE.
16. 如图,在△ABC和△DEF中,B,E,C,F在同一直线上,下面有四个条件:
①AB=DE;②AC=DF;③AB∥DE;④BE=CF.请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
解:我写的真命题是:
已知: ;
求证: .(注:不能只填序号)
证明如下:
四、(本大题共2小题,每小题8分,满分16分)
17. 已知:如图,△ABC≌△A'B'C,∠A:∠BCA:∠ABC=3:10:5,求∠A',∠B'BC的度数.
18. 如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)求证:△ABE≌△DBE.
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,点A,E,F,C在同一直线上,DE∥BF,DE=BF,AE=CF.
(1)证明:△ABF≌△CDE.
(2)若DE=DF=CF且∠A=20°,求∠EDF的度数.
20. 已知:△ABC≌△EDC.
(1)若DE∥BC(如图1),判断△ABC的形状并说明理由.
(2)连接BE交AC于点F,点H是CE上的点,且CH=CF,连接DH交BE于点K,(如图2)求证:∠DKF =∠ACB.
六、(本题满分12分)
21. 如图,已知在△ABC和△AEF中, . BE 交FC于点 O,
(1)求证:BE=CF.
(2)当∠BAC=70°时,求∠BOC的度数.
七、(本题满分12分)
22. 已知:如图1,线段AB,CD相交于点O,连接AD,CB,如图2,在图1的条件下,. 和 的平分线AP和CP相交于点 P,并且与CD,AB分别相交于点 M,N.试解答下列问题:
(1)在图1中,请直接写出∠A,∠B,∠C,∠D之间的数量关系: .
(2)在图2中,若 试求 的度数.(写出解答过程)
(3)如果图2中∠D 和∠B为任意角,其他条件不变,直接写出 与 之间的数量关系.(直接写出结论)
八、(本题满分14分)
23.“综合与实践”学习小组准备制作一组三角形,记这些三角形的三边分别为a,b,c,用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,4,4)表示边长分别为2,4,4个单位长度的一个三角形.
(1)若这些三角形三边的长度为大于0且小于3 的整数个单位长度,请用记号写出所有满足条件的三角形.
(2)如图,AD是 的中线,线段AB,AC的长度分别为2个,6个单位长度,且线段AD 的长度为整数个单位长度,过点C作( 交AD的延长线于点 E.
①求 DE 之长.
②请直接用记号表示△ACE.
专项练习(二)
1. B 2. B 3. D 4. D 5. A 6. A 7. C 8. C 9. C 10. B
11.当a=2,b=1时,a>b,但
12.3 13.13 14.70°
15.证明:∵FC∥AB,∴∠A=∠FCE,∠ADE=∠F,在△ADE与△CFE中,
∴△ADE≌△CFE(AAS).
16.解:我写的真命题是:已知:①AB=DE,②AC=DF,④BE=CF,求证:③AB∥DE.
证明如下:∵ BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS),
∴∠B=∠DEF,∴AB∥DE.(答案不唯一)
17.解:∵∠A:∠BCA:∠ABC=3:10:5,设∠A=3x,则∠ABC=5x,∠BCA=10x.
∵∠A+∠ABC+∠BCA=180°,
∴3x+5x+10x=180°,x=10°.
∴∠A=30°,∠ABC=50°,∠BCA=100°.
∵△ABC≌△A'B'C,
∴∠A'=∠A=30°,∠B'=∠ABC=50°,B'C=BC,
∴△CBB'为等腰三角形,∴∠B'BC=∠B'=50°.
18.(1)证明:∵BE平分∠ABC,∴∠ABE=∠DBE,在△ABE和△DBE中, ∴△ABE≌△DBE(SAS).
(2)解:∵∠A=100°,∠C=50°,∴∠ABC=30°,
∵ BE平分
在△ABE中,∠AEB=180°-∠A-∠ABE=180°-100°-15°=65°.
解:证明:∵AE=CF,∴AE+EF=CF+EF即AF=CE,∵ BF∥DE,∴∠DEF=∠BFE.
在△ABF与△CDE中,
∴△ABF≌△CDE(SAS).
(2)解:∵△ABF≌△CDE,∴∠A=∠C=20°,
∵DF=CF,∴∠C=∠CDF=20°,∴∠DFE=2∠C=40°,
∵ DE=DF,∴∠DFE=∠DEF=40°,
∴∠EDF=180°-2∠DFE=180°-2×40°=100°.
20.(1)解:∵△ABC≌△EDC,
∴∠ABC=∠EDC,∠ACB=∠ECD,
∵ DE∥BC,∴∠EDC=∠ACB,
∴∠ABC=∠ACB,∴AB=AC,
∴△ABC是等腰三角形.
(2)证明:∵△ABC≌△EDC,∴BC=CD,∠ACB=∠DCE,
在△BCF和△DCH中,
∴△BCF≌△DCH(SAS),∴∠FBC=∠HDC,在△FBC和△FDK中,
∵∠FBC=∠FDK,∠BFC=∠DFK,
∴∠DKF=∠BCF,即∠DKF=∠ACB.
21.(1)证明:∵∠CAB=∠EAF,
∴∠CAB+∠CAE=∠EAF+∠CAE,
∴∠BAE=∠CAF,在△BAE和△CAF中,
∴△BAE≌△CAF(SAS),∴BE=CF.(2)解:∵△BAE≌△CAF,∴∠EBA=∠FCA,
即∠DBA=∠OCD,∵ ∠BDA=∠ODC,
∴∠BAD=∠COD,即∠BAC=∠BOC,
∵∠BAC=70°,∴即∠BOC=70°.
22.解:(1)∵∠A+∠D+∠AOD=∠B+∠C+∠BOC=180°,∠AOD=∠BOC,∴∠A+∠D=∠B+∠C.
故答案为:∠A+∠D=∠B+∠C.
(2)由(1)已知,∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,
∴∠1--∠3=∠P--∠D,∠2--∠4=∠B--∠P,
又∵AP,CP分别平分∠DAB和∠BCD,
∴∠1=∠2,∠3=∠4,∴∠P--∠D=∠B--∠P,
即2∠P=∠B+∠D,∴∠P=(50°+40°)÷2=45°.
(3)2∠P=∠B+∠D.
23.解:(1)由三角形的三边关系得所有满足条件的三角形为.(1,1,1),(1,2,2),(2,2,2).
(2)①∵CE∥AB,∴∠B=∠ECD,∠BAD=∠E,
∵AD是△ABC的中线,∴ BD=CD.
在△ABD和△ECD中,
∴ △ABD≌△ECD(AAS).
∴AD=ED,AB=CE=2,∴AE=2AD,在△ACE中,AC-CE∴6-2<2AD<6+2,∴2∵线段AD的长度为整数个单位长度,
∴AD=3,∴ED=3.
②AE=2AD=6,用记号表示△ACE为(2,6,6).
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 下列命题中是假命题的是 ( )
A.对顶角相等 B.同旁内角互补 C.两点确定一条直线 D.垂线段最短
2. 下列图形中,具有稳定性的是 ( )
3. 已知△ABC的三边长分别为a,b,c,且M=(a+b+c)(a+b-c)(a-b-c),那么 ( )
A. M>0 B. M≥0 C. M=0 D. M<0
4. 已知△ABC≌△A1B1C1,A和A1对应,B和B1对应,∠A=70°,∠B1=50°,则∠C的度数为 ( )
A.70° B.50° C.120° D.60°
5. 如图,△ABC中,点D在BC的延长线上,则下列结论一定成立的是 ( )
A.∠1 =∠A +∠B B.∠1 =∠2+∠A C.∠1 =∠2+∠B D.∠2=∠A+∠B
6. 如图,PA⊥OM,PB⊥ON,垂足分别为A,B,PA=PB.则△OAP≌△OBP 的依据不可能是( )
A. SSS B. SAS C. AAS D. HL
7. 如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC 与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB 与∠DEF 的度数和为 ( )
A.60° B.75° C.90° D.120°
如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①CE=BF;②△ACE和△CDE面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9. 如图,在△ABC和△A'B'C中,△ABC≌△A'B'C,AA'∥BC,∠ACB=α,∠BCB'=β,则α,β满足关系 ( )
A.α+β=90° B.α+2β=180° C.2α+β=180° D.α+β=180°
10. 如图,已知E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,添加以下条件之一,仍不能证明△ABC≌△DEF的是 ( )
A.∠E=∠ABC B. AB=DE C. AB∥DE D. DF∥AC
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 为说明命题“如果a>b,那么 是假命题,你举出的一个反例是
12. 如图,BA⊥AC,CD∥AB,BC=DE,且BC⊥DE,若AB=5,CD=8,则AE= .
13. 7 条长度均为整数的线段a1,a ,a ,a ,a ,a ,a 满足 且这7条线段中的任意3条都不能构成三角形.若 厘米,a =21厘米,则a 的值是 .
14. 如图,在等腰△ABC中,AB=AC,∠A=20°. AB上一点D,使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE= °.
三、(本大题共2小题,每小题8分,满分16分)
15. (广州中考)如图,D 是AB 上一点,DF 交 AC 于点 E,DE =FE,FC∥AB,求证:△ADE≌△CFE.
16. 如图,在△ABC和△DEF中,B,E,C,F在同一直线上,下面有四个条件:
①AB=DE;②AC=DF;③AB∥DE;④BE=CF.请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
解:我写的真命题是:
已知: ;
求证: .(注:不能只填序号)
证明如下:
四、(本大题共2小题,每小题8分,满分16分)
17. 已知:如图,△ABC≌△A'B'C,∠A:∠BCA:∠ABC=3:10:5,求∠A',∠B'BC的度数.
18. 如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)求证:△ABE≌△DBE.
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
五、(本大题共2小题,每小题10分,满分20分)
19. 如图,点A,E,F,C在同一直线上,DE∥BF,DE=BF,AE=CF.
(1)证明:△ABF≌△CDE.
(2)若DE=DF=CF且∠A=20°,求∠EDF的度数.
20. 已知:△ABC≌△EDC.
(1)若DE∥BC(如图1),判断△ABC的形状并说明理由.
(2)连接BE交AC于点F,点H是CE上的点,且CH=CF,连接DH交BE于点K,(如图2)求证:∠DKF =∠ACB.
六、(本题满分12分)
21. 如图,已知在△ABC和△AEF中, . BE 交FC于点 O,
(1)求证:BE=CF.
(2)当∠BAC=70°时,求∠BOC的度数.
七、(本题满分12分)
22. 已知:如图1,线段AB,CD相交于点O,连接AD,CB,如图2,在图1的条件下,. 和 的平分线AP和CP相交于点 P,并且与CD,AB分别相交于点 M,N.试解答下列问题:
(1)在图1中,请直接写出∠A,∠B,∠C,∠D之间的数量关系: .
(2)在图2中,若 试求 的度数.(写出解答过程)
(3)如果图2中∠D 和∠B为任意角,其他条件不变,直接写出 与 之间的数量关系.(直接写出结论)
八、(本题满分14分)
23.“综合与实践”学习小组准备制作一组三角形,记这些三角形的三边分别为a,b,c,用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,4,4)表示边长分别为2,4,4个单位长度的一个三角形.
(1)若这些三角形三边的长度为大于0且小于3 的整数个单位长度,请用记号写出所有满足条件的三角形.
(2)如图,AD是 的中线,线段AB,AC的长度分别为2个,6个单位长度,且线段AD 的长度为整数个单位长度,过点C作( 交AD的延长线于点 E.
①求 DE 之长.
②请直接用记号表示△ACE.
专项练习(二)
1. B 2. B 3. D 4. D 5. A 6. A 7. C 8. C 9. C 10. B
11.当a=2,b=1时,a>b,但
12.3 13.13 14.70°
15.证明:∵FC∥AB,∴∠A=∠FCE,∠ADE=∠F,在△ADE与△CFE中,
∴△ADE≌△CFE(AAS).
16.解:我写的真命题是:已知:①AB=DE,②AC=DF,④BE=CF,求证:③AB∥DE.
证明如下:∵ BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS),
∴∠B=∠DEF,∴AB∥DE.(答案不唯一)
17.解:∵∠A:∠BCA:∠ABC=3:10:5,设∠A=3x,则∠ABC=5x,∠BCA=10x.
∵∠A+∠ABC+∠BCA=180°,
∴3x+5x+10x=180°,x=10°.
∴∠A=30°,∠ABC=50°,∠BCA=100°.
∵△ABC≌△A'B'C,
∴∠A'=∠A=30°,∠B'=∠ABC=50°,B'C=BC,
∴△CBB'为等腰三角形,∴∠B'BC=∠B'=50°.
18.(1)证明:∵BE平分∠ABC,∴∠ABE=∠DBE,在△ABE和△DBE中, ∴△ABE≌△DBE(SAS).
(2)解:∵∠A=100°,∠C=50°,∴∠ABC=30°,
∵ BE平分
在△ABE中,∠AEB=180°-∠A-∠ABE=180°-100°-15°=65°.
解:证明:∵AE=CF,∴AE+EF=CF+EF即AF=CE,∵ BF∥DE,∴∠DEF=∠BFE.
在△ABF与△CDE中,
∴△ABF≌△CDE(SAS).
(2)解:∵△ABF≌△CDE,∴∠A=∠C=20°,
∵DF=CF,∴∠C=∠CDF=20°,∴∠DFE=2∠C=40°,
∵ DE=DF,∴∠DFE=∠DEF=40°,
∴∠EDF=180°-2∠DFE=180°-2×40°=100°.
20.(1)解:∵△ABC≌△EDC,
∴∠ABC=∠EDC,∠ACB=∠ECD,
∵ DE∥BC,∴∠EDC=∠ACB,
∴∠ABC=∠ACB,∴AB=AC,
∴△ABC是等腰三角形.
(2)证明:∵△ABC≌△EDC,∴BC=CD,∠ACB=∠DCE,
在△BCF和△DCH中,
∴△BCF≌△DCH(SAS),∴∠FBC=∠HDC,在△FBC和△FDK中,
∵∠FBC=∠FDK,∠BFC=∠DFK,
∴∠DKF=∠BCF,即∠DKF=∠ACB.
21.(1)证明:∵∠CAB=∠EAF,
∴∠CAB+∠CAE=∠EAF+∠CAE,
∴∠BAE=∠CAF,在△BAE和△CAF中,
∴△BAE≌△CAF(SAS),∴BE=CF.(2)解:∵△BAE≌△CAF,∴∠EBA=∠FCA,
即∠DBA=∠OCD,∵ ∠BDA=∠ODC,
∴∠BAD=∠COD,即∠BAC=∠BOC,
∵∠BAC=70°,∴即∠BOC=70°.
22.解:(1)∵∠A+∠D+∠AOD=∠B+∠C+∠BOC=180°,∠AOD=∠BOC,∴∠A+∠D=∠B+∠C.
故答案为:∠A+∠D=∠B+∠C.
(2)由(1)已知,∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,
∴∠1--∠3=∠P--∠D,∠2--∠4=∠B--∠P,
又∵AP,CP分别平分∠DAB和∠BCD,
∴∠1=∠2,∠3=∠4,∴∠P--∠D=∠B--∠P,
即2∠P=∠B+∠D,∴∠P=(50°+40°)÷2=45°.
(3)2∠P=∠B+∠D.
23.解:(1)由三角形的三边关系得所有满足条件的三角形为.(1,1,1),(1,2,2),(2,2,2).
(2)①∵CE∥AB,∴∠B=∠ECD,∠BAD=∠E,
∵AD是△ABC的中线,∴ BD=CD.
在△ABD和△ECD中,
∴ △ABD≌△ECD(AAS).
∴AD=ED,AB=CE=2,∴AE=2AD,在△ACE中,AC-CE
∴AD=3,∴ED=3.
②AE=2AD=6,用记号表示△ACE为(2,6,6).
