沪科版数学八年级上册 专项练习(三)第15章 轴对称图形与等腰三角形 (含答案)
文档属性
| 名称 | 沪科版数学八年级上册 专项练习(三)第15章 轴对称图形与等腰三角形 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-14 00:00:00 | ||
图片预览


文档简介
专项练习(三)轴对称图形与等腰三角形
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
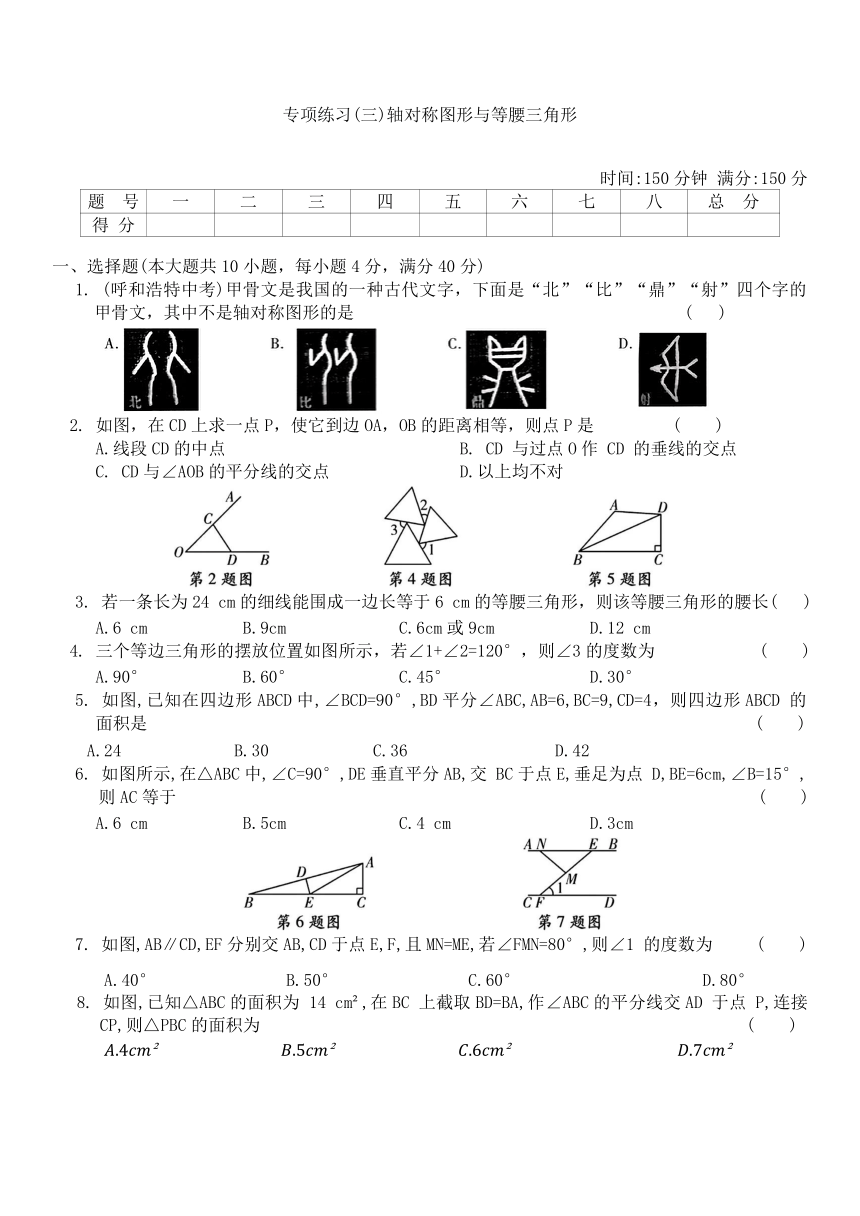
1. (呼和浩特中考)甲骨文是我国的一种古代文字,下面是“北”“比”“鼎”“射”四个字的甲骨文,其中不是轴对称图形的是 ( )
2. 如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是 ( )
A.线段CD的中点 B. CD 与过点O作 CD 的垂线的交点
C. CD与∠AOB的平分线的交点 D.以上均不对
3. 若一条长为24 cm的细线能围成一边长等于6 cm的等腰三角形,则该等腰三角形的腰长( )
A.6 cm B.9cm C.6cm或9cm D.12 cm
4. 三个等边三角形的摆放位置如图所示,若∠1+∠2=120°,则∠3的度数为 ( )
A.90° B.60° C.45° D.30°
5. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD 的面积是 ( )
A.24 B.30 C.36 D.42
6. 如图所示,在△ABC中,∠C=90°,DE垂直平分AB,交 BC于点E,垂足为点 D,BE=6cm,∠B=15°,则AC等于 ( )
A.6 cm B.5cm C.4 cm D.3cm
7. 如图,AB∥CD,EF分别交AB,CD于点E,F,且MN=ME,若∠FMN=80°,则∠1 的度数为 ( )
A.40° B.50° C.60° D.80°
8. 如图,已知△ABC的面积为 14 cm ,在BC 上截取BD=BA,作∠ABC的平分线交AD 于点 P,连接CP,则△PBC的面积为 ( )
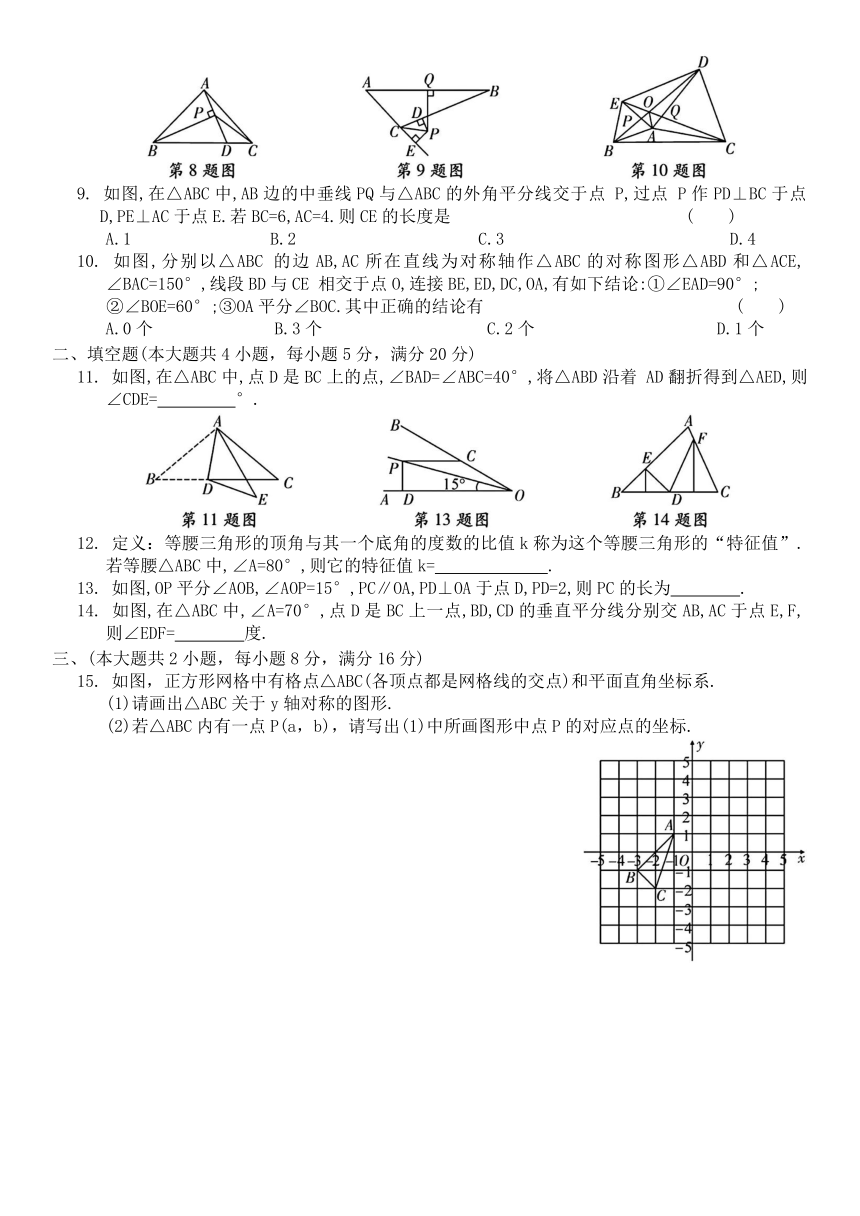
9. 如图,在△ABC中,AB边的中垂线PQ与△ABC的外角平分线交于点 P,过点 P作PD⊥BC于点D,PE⊥AC于点E.若BC=6,AC=4.则CE的长度是 ( )
A.1 B.2 C.3 D.4
10. 如图,分别以△ABC 的边AB,AC所在直线为对称轴作△ABC的对称图形△ABD和△ACE, ∠BAC=150°,线段BD与CE 相交于点O,连接BE,ED,DC,OA,有如下结论:①∠EAD=90°;
②∠BOE=60°;③OA平分∠BOC.其中正确的结论有 ( )
A.0个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着 AD翻折得到△AED,则∠CDE= °.
12. 定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k= .
13. 如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PD=2,则PC的长为 .
14. 如图,在△ABC中,∠A=70°,点D是BC上一点,BD,CD的垂直平分线分别交AB,AC于点E,F,则∠EDF= 度.
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,正方形网格中有格点△ABC(各顶点都是网格线的交点)和平面直角坐标系.
(1)请画出△ABC关于y轴对称的图形.
(2)若△ABC内有一点P(a,b),请写出(1)中所画图形中点P的对应点的坐标.
16. 如图,在Rt△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,DE⊥AC于点E,BF∥DE交CD 于点 F.求证:DE=BF.
四、(本大题共2小题,每小题8分,满分16分)
17. 如图,已知AB比AC长3cm,BC的垂直平分线交AB 于点 D,交 BC于点 E,△ACD 的周长是14 cm,求AB和AC的长.
18. 如图,已知等边△ABC中,BD⊥AC,垂足为D,E是BC延长线上的一点,且CE=CD.
(1)求证:BD=DE.
(2)若M为BE中点,求证:DM平分∠BDE.
五、(本大题共2 小题,每小题10分,满分20分)
19. 已知:如图,在等腰三角形ADC中,AD=CD,且AB∥DC,CB⊥AB于点B. CE⊥AD交AD的延长线于点 E.
(1)求证:CE=CB.
(2)如果连接BE,请写出 BE 与 AC 的关系并证明.
20. 如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC.
(1)求证:∠BAD=2∠MAN.
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC.
六、(本题满分12分)
21. 在△ABC中,∠ABC与∠ACB的角平分线BO,CO相交于点O,连接AO,过点O作EF∥BC交AB,AC于点E,F,AB=5,AC=4.
(1)求△AEF的周长.
(2)若点O到BC距离为4,求△OAB的面积.
七、(本题满分12分)
22. 在△ABC和△DCE中,CA=CB,CD=CE,∠CAB=∠CED=α.
(1)如图1,将AD,EB延长,延长线相交于点 O.
①求证:BE=AD.
②用含α的式子表示∠AOB的度数(直接写出结果).
(2)如图2,当α=45°时,连接BD,AE,作CM⊥AE 于点M,延长MC与BD交于点N,求证:N是 BD的中点.
八、(本题满分14分)
23. 如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接 DE.
(1)如图1,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数.
(2)如图2,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数.
(3)当点 D 在直线BC上(不与点 B,C 重合)运动时,试探究∠BAD 与∠CDE 的数量关系,并说明理由.
专项练习(三)
1. B 2. C 3. B 4. B 5. B 6. D 7. A 8. D 9. A 10. B 11.20 或
13.4 14.70
15.解:(1)△ABC关于y轴对称的图形. 如图所示.
(2)点P的对应点的坐标为( -a,b).
16.证明:∵CD平分∠ACB,DE⊥AC,∠ABC=90°,
∴∠ABC=∠DEC,DE=BD,
∵∠BDC=90°--∠BCD,∠EDC=90°--∠ACD,
∴∠BDC=∠EDC,∵BF∥DE,∴∠BFD=∠EDC,
∴∠BDC=∠BFD,∴BD=BF,∴DE=BF.
17.解:∵ DE是BC的垂直平分线,∴CD=BD,
∴△ACD的周长=AC+AD+CD=AC+AD+BD=AC+AB,
由题意,得{AB+AC=33,解得{AB=5.5}
∴AB和AC的长分别为8.5cm,5.5cm.
证明:(1)∵△ABC是等边三角形,BD⊥AC,
∵CD=CE,∴∠CDE=∠E,
∵∠ACB=∠CDE+∠E=60°,∴∠E=30°,
∴∠DBE=∠E,∴BD=DE.
(2)∵BD=DE,M为BE中点,
∴DM⊥BE,BM=EM,
∴DM平分∠BDE.
19.证明:(1)∵AD=CD,∴∠DAC=∠DCA,
∵AB∥CD,∴∠DCA=∠CAB,∴∠DCA=∠CAB,
∴AC是∠EAB是角平分线,
∵CE⊥AE,CB⊥AB,∴CE=CB.
(2)∵CE⊥AE,CB⊥AB,
∴∠CEA=∠CBA=90°,
在 Rt△CEA 和Rt△CBA中,{CE=CB,
∴ Rt△CEA≌Rt△CBA(HL),
∴AE=AB,CE=CB,
∴点A、点C在线段BE的垂直平分线上,
∴AC垂直平分BE.
20.(1)证明:连接AC,
∵M是CD的中点,AM⊥CD,
∴AM 是线段CD的垂直平分线,
∴AC=AD,又AM⊥CD,∴∠DAM=∠CAM.同理,∠BAN=∠CAN.
∵∠BAD=∠BAN+∠CAN+∠DAM+∠CAM,
∴∠BAD=2(∠CAN+∠CAM),
∴∠MAN=∠CAN+∠CAM,
∴∠BAD =2∠MAN.
(2)解:∵AM⊥CD,AN⊥BC,∠MAN=70°,
∴∠BCD=360°-90°-90°-70°=110°,
∴∠BDC=180°-∠DBC--∠BCD=30°,
由(1)得∠BAD=2∠MAN,
∵∠MAN=70°,∴∠BAD =140°,
∵AB=AC,AD=AC,∴AB=AD,
∴∠ADB=∠ABD=(180°-140°)÷2=20°,
∴∠ADC=∠ADB+∠BDC=50°.
21.解:(1)∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=∠OBC,∠FCO=∠OCB,
∵EF∥BC,∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴OE=BE,OF=CF,∵AB=5,AC=4,
∴△AEF的周长=AE+EF +AF=AE +BE+CF+AF =AB+AC=5+4=9.
(2)过O作OM⊥AB于M,ON⊥BC于N,∵BO平分∠ABC,∴OM=ON,
∵点O到BC距离为4,
∴ON=OM=4,∵AB=5,
∴△OAB的面积
22.(1)①证明:∵CA=CB,CD=CE,∠CAB=∠CED=α,∴∠ACB=180°-2α,∠DCE=180°-2α,
∴ ∠ACB = ∠DCE,∴ ∠ACB ∠DCB = ∠DCE-∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),∴BE=AD.
②解:∵△ACD≌△BCE,∴∠CAD=∠CBE=α+∠BAO,
∵∠ABE=∠AOB+∠BAO,
∴∠CBE+α=∠AOB+∠BAO,
∴∠BAO+α+α=∠AOB+∠BAO,
∴∠AOB=2α.
(2)证明:如图,作BP⊥MN交MN的延长线于点 P,作 DQ⊥MN于点Q,
∵∠BCP+∠BCA=∠CAM+∠AMC,
∵ ∠BCA=∠AMC,∴∠BCP=∠CAM,
在△CBP与△ACM中,
∴△CBP≌△ACM(AAS),∴MC=BP,同理,CM=DQ,∴DQ=BP,
在△BPN与△DQN中,
∴△BPN≌△DQN(AAS),
∴BN=ND,∴N是BD的中点.
23.解:(1)∵∠B=∠C=35°,∴∠BAC=110°,
∵∠BAD=80°,∴∠DAE=30°,∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠CDE=∠AED-∠C=40°.
(2)∵∠ACB=75°,∠CDE=18°,
∴∠E=75°-18°=57°,∵AD=AE,
∴∠ADE=∠AED=57°,∴∠ADC=39°,
∵∠ABC=∠ADB+∠DAB=75°,∴∠BAD=36°.
(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β.
i )如图1,当点 D 在点 B的左侧时,∠ADC=x°-α,
①-②得2α-β=0,∴2α=β.
ii)如图2,当点 D在线段BC上时,
,
②-①得α=β-α,∴2α=β.
iii)如图3,当点D在点 C右侧时,
②-①得2α-β=0,∴2α=β.
综上所述,∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. (呼和浩特中考)甲骨文是我国的一种古代文字,下面是“北”“比”“鼎”“射”四个字的甲骨文,其中不是轴对称图形的是 ( )
2. 如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是 ( )
A.线段CD的中点 B. CD 与过点O作 CD 的垂线的交点
C. CD与∠AOB的平分线的交点 D.以上均不对
3. 若一条长为24 cm的细线能围成一边长等于6 cm的等腰三角形,则该等腰三角形的腰长( )
A.6 cm B.9cm C.6cm或9cm D.12 cm
4. 三个等边三角形的摆放位置如图所示,若∠1+∠2=120°,则∠3的度数为 ( )
A.90° B.60° C.45° D.30°
5. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD 的面积是 ( )
A.24 B.30 C.36 D.42
6. 如图所示,在△ABC中,∠C=90°,DE垂直平分AB,交 BC于点E,垂足为点 D,BE=6cm,∠B=15°,则AC等于 ( )
A.6 cm B.5cm C.4 cm D.3cm
7. 如图,AB∥CD,EF分别交AB,CD于点E,F,且MN=ME,若∠FMN=80°,则∠1 的度数为 ( )
A.40° B.50° C.60° D.80°
8. 如图,已知△ABC的面积为 14 cm ,在BC 上截取BD=BA,作∠ABC的平分线交AD 于点 P,连接CP,则△PBC的面积为 ( )
9. 如图,在△ABC中,AB边的中垂线PQ与△ABC的外角平分线交于点 P,过点 P作PD⊥BC于点D,PE⊥AC于点E.若BC=6,AC=4.则CE的长度是 ( )
A.1 B.2 C.3 D.4
10. 如图,分别以△ABC 的边AB,AC所在直线为对称轴作△ABC的对称图形△ABD和△ACE, ∠BAC=150°,线段BD与CE 相交于点O,连接BE,ED,DC,OA,有如下结论:①∠EAD=90°;
②∠BOE=60°;③OA平分∠BOC.其中正确的结论有 ( )
A.0个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着 AD翻折得到△AED,则∠CDE= °.
12. 定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k= .
13. 如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PD=2,则PC的长为 .
14. 如图,在△ABC中,∠A=70°,点D是BC上一点,BD,CD的垂直平分线分别交AB,AC于点E,F,则∠EDF= 度.
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,正方形网格中有格点△ABC(各顶点都是网格线的交点)和平面直角坐标系.
(1)请画出△ABC关于y轴对称的图形.
(2)若△ABC内有一点P(a,b),请写出(1)中所画图形中点P的对应点的坐标.
16. 如图,在Rt△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,DE⊥AC于点E,BF∥DE交CD 于点 F.求证:DE=BF.
四、(本大题共2小题,每小题8分,满分16分)
17. 如图,已知AB比AC长3cm,BC的垂直平分线交AB 于点 D,交 BC于点 E,△ACD 的周长是14 cm,求AB和AC的长.
18. 如图,已知等边△ABC中,BD⊥AC,垂足为D,E是BC延长线上的一点,且CE=CD.
(1)求证:BD=DE.
(2)若M为BE中点,求证:DM平分∠BDE.
五、(本大题共2 小题,每小题10分,满分20分)
19. 已知:如图,在等腰三角形ADC中,AD=CD,且AB∥DC,CB⊥AB于点B. CE⊥AD交AD的延长线于点 E.
(1)求证:CE=CB.
(2)如果连接BE,请写出 BE 与 AC 的关系并证明.
20. 如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC.
(1)求证:∠BAD=2∠MAN.
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC.
六、(本题满分12分)
21. 在△ABC中,∠ABC与∠ACB的角平分线BO,CO相交于点O,连接AO,过点O作EF∥BC交AB,AC于点E,F,AB=5,AC=4.
(1)求△AEF的周长.
(2)若点O到BC距离为4,求△OAB的面积.
七、(本题满分12分)
22. 在△ABC和△DCE中,CA=CB,CD=CE,∠CAB=∠CED=α.
(1)如图1,将AD,EB延长,延长线相交于点 O.
①求证:BE=AD.
②用含α的式子表示∠AOB的度数(直接写出结果).
(2)如图2,当α=45°时,连接BD,AE,作CM⊥AE 于点M,延长MC与BD交于点N,求证:N是 BD的中点.
八、(本题满分14分)
23. 如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接 DE.
(1)如图1,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数.
(2)如图2,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数.
(3)当点 D 在直线BC上(不与点 B,C 重合)运动时,试探究∠BAD 与∠CDE 的数量关系,并说明理由.
专项练习(三)
1. B 2. C 3. B 4. B 5. B 6. D 7. A 8. D 9. A 10. B 11.20 或
13.4 14.70
15.解:(1)△ABC关于y轴对称的图形. 如图所示.
(2)点P的对应点的坐标为( -a,b).
16.证明:∵CD平分∠ACB,DE⊥AC,∠ABC=90°,
∴∠ABC=∠DEC,DE=BD,
∵∠BDC=90°--∠BCD,∠EDC=90°--∠ACD,
∴∠BDC=∠EDC,∵BF∥DE,∴∠BFD=∠EDC,
∴∠BDC=∠BFD,∴BD=BF,∴DE=BF.
17.解:∵ DE是BC的垂直平分线,∴CD=BD,
∴△ACD的周长=AC+AD+CD=AC+AD+BD=AC+AB,
由题意,得{AB+AC=33,解得{AB=5.5}
∴AB和AC的长分别为8.5cm,5.5cm.
证明:(1)∵△ABC是等边三角形,BD⊥AC,
∵CD=CE,∴∠CDE=∠E,
∵∠ACB=∠CDE+∠E=60°,∴∠E=30°,
∴∠DBE=∠E,∴BD=DE.
(2)∵BD=DE,M为BE中点,
∴DM⊥BE,BM=EM,
∴DM平分∠BDE.
19.证明:(1)∵AD=CD,∴∠DAC=∠DCA,
∵AB∥CD,∴∠DCA=∠CAB,∴∠DCA=∠CAB,
∴AC是∠EAB是角平分线,
∵CE⊥AE,CB⊥AB,∴CE=CB.
(2)∵CE⊥AE,CB⊥AB,
∴∠CEA=∠CBA=90°,
在 Rt△CEA 和Rt△CBA中,{CE=CB,
∴ Rt△CEA≌Rt△CBA(HL),
∴AE=AB,CE=CB,
∴点A、点C在线段BE的垂直平分线上,
∴AC垂直平分BE.
20.(1)证明:连接AC,
∵M是CD的中点,AM⊥CD,
∴AM 是线段CD的垂直平分线,
∴AC=AD,又AM⊥CD,∴∠DAM=∠CAM.同理,∠BAN=∠CAN.
∵∠BAD=∠BAN+∠CAN+∠DAM+∠CAM,
∴∠BAD=2(∠CAN+∠CAM),
∴∠MAN=∠CAN+∠CAM,
∴∠BAD =2∠MAN.
(2)解:∵AM⊥CD,AN⊥BC,∠MAN=70°,
∴∠BCD=360°-90°-90°-70°=110°,
∴∠BDC=180°-∠DBC--∠BCD=30°,
由(1)得∠BAD=2∠MAN,
∵∠MAN=70°,∴∠BAD =140°,
∵AB=AC,AD=AC,∴AB=AD,
∴∠ADB=∠ABD=(180°-140°)÷2=20°,
∴∠ADC=∠ADB+∠BDC=50°.
21.解:(1)∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=∠OBC,∠FCO=∠OCB,
∵EF∥BC,∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴OE=BE,OF=CF,∵AB=5,AC=4,
∴△AEF的周长=AE+EF +AF=AE +BE+CF+AF =AB+AC=5+4=9.
(2)过O作OM⊥AB于M,ON⊥BC于N,∵BO平分∠ABC,∴OM=ON,
∵点O到BC距离为4,
∴ON=OM=4,∵AB=5,
∴△OAB的面积
22.(1)①证明:∵CA=CB,CD=CE,∠CAB=∠CED=α,∴∠ACB=180°-2α,∠DCE=180°-2α,
∴ ∠ACB = ∠DCE,∴ ∠ACB ∠DCB = ∠DCE-∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),∴BE=AD.
②解:∵△ACD≌△BCE,∴∠CAD=∠CBE=α+∠BAO,
∵∠ABE=∠AOB+∠BAO,
∴∠CBE+α=∠AOB+∠BAO,
∴∠BAO+α+α=∠AOB+∠BAO,
∴∠AOB=2α.
(2)证明:如图,作BP⊥MN交MN的延长线于点 P,作 DQ⊥MN于点Q,
∵∠BCP+∠BCA=∠CAM+∠AMC,
∵ ∠BCA=∠AMC,∴∠BCP=∠CAM,
在△CBP与△ACM中,
∴△CBP≌△ACM(AAS),∴MC=BP,同理,CM=DQ,∴DQ=BP,
在△BPN与△DQN中,
∴△BPN≌△DQN(AAS),
∴BN=ND,∴N是BD的中点.
23.解:(1)∵∠B=∠C=35°,∴∠BAC=110°,
∵∠BAD=80°,∴∠DAE=30°,∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠CDE=∠AED-∠C=40°.
(2)∵∠ACB=75°,∠CDE=18°,
∴∠E=75°-18°=57°,∵AD=AE,
∴∠ADE=∠AED=57°,∴∠ADC=39°,
∵∠ABC=∠ADB+∠DAB=75°,∴∠BAD=36°.
(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β.
i )如图1,当点 D 在点 B的左侧时,∠ADC=x°-α,
①-②得2α-β=0,∴2α=β.
ii)如图2,当点 D在线段BC上时,
,
②-①得α=β-α,∴2α=β.
iii)如图3,当点D在点 C右侧时,
②-①得2α-β=0,∴2α=β.
综上所述,∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.
