物理人教版(2019)选择性必修第二册1.4质谱仪与回旋加速器(共17张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第二册1.4质谱仪与回旋加速器(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 455.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-14 07:57:51 | ||
图片预览





文档简介
(共17张PPT)
4.质谱仪与回旋加速器
要认识原子核内部的情况,
必须把核“打开”进行“观察”。
然而原子核被强大的核力约束,
只有用极高能量的粒子作为“炮弹”去轰击,才能把它“打开”。
产生这些高能“炮弹”的“工厂”就是各种各样的粒子加速器。
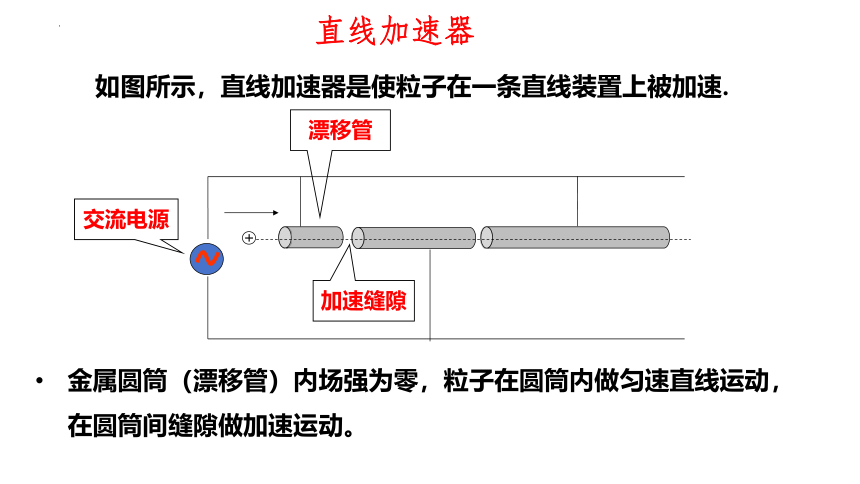
金属圆筒(漂移管)内场强为零,粒子在圆筒内做匀速直线运动,在圆筒间缝隙做加速运动。
直线加速器
如图所示,直线加速器是使粒子在一条直线装置上被加速.
漂移管
加速缝隙
交流电源
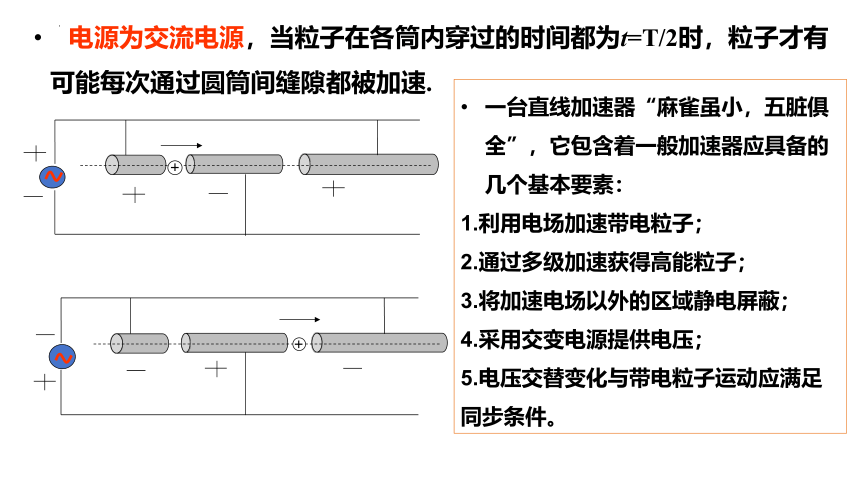
电源为交流电源,当粒子在各筒内穿过的时间都为t=T/2时,粒子才有可能每次通过圆筒间缝隙都被加速.
一台直线加速器“麻雀虽小,五脏俱全”,它包含着一般加速器应具备的几个基本要素:
1.利用电场加速带电粒子;
2.通过多级加速获得高能粒子;
3.将加速电场以外的区域静电屏蔽;
4.采用交变电源提供电压;
5.电压交替变化与带电粒子运动应满足同步条件。
能不能建造一种加速器,在较小的空间范围内让粒子经过多次加速获得所需要的能量呢?
1932年美国科学家劳伦斯发明了回旋加速器,巧妙的应用带电粒子在磁场中运动特点解决了这一问题。
直线加速器的缺点:
体积通常较大,占地面积大。
一. 回旋加速器
1.构造:
运动一周加速两次,v、r变大,但周期不变
3.最大动能:
4.加速次数:
2.原理:
(t与q,m无关)
(由B,Rm决定)
如图,D1、D2是半圆金属盒,D形盒处于匀强磁场中,D形盒的缝隙处接交流电源.
电场使粒子加速(加速过程时间极短,忽略不计),磁场使粒子回旋(匀速圆周运动)
问题1:要让粒子持续加速,T交与T圆满足什么关系?
问题2:粒子运动一周,加速几次?v,r,T如何变?
T交=T圆
f交=f圆
n=Ekm/qU
5.运动总时间:
(n与U有关)
美国物理学家 劳伦斯
1932年,美国物理学家劳伦斯正是沿着与上述相仿的巧妙思路,发明了回旋加速器,从而使人类在获得具有较高能量的粒子方面迈进了一大步。为此,劳伦斯获得了1939年的诺贝尔物理学奖。
1.如图甲所示是用来加速带电粒子的回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,两盒分别与高频交流电源相连。带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示。忽略带电粒子在电场中的加速时间,则下列判断正确的是( )
A.在Ek-t图像中应有t4-t3B.加速电压越大,粒子最后获得的动能就越大
C.粒子加速次数越多,粒子最大动能一定越大
D.要想粒子获得的最大动能增大,可增加D形盒的面积
D
2. (多选)1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示。这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙,所加交变电压极性变化时,电压值不变。下列说法正确的是( )
A.所加交变电压的周期等于带电粒子圆周运动周期的一半
B.利用回旋加速器加速带电粒子,要提高加速粒子的最终能量,应尽可能增大磁感应强度B和D形盒的半径R
C.回旋加速器的加速电压越大,带电粒子获得的最大动能越大
D.粒子每次经过D形盒狭缝时,电场力对粒子做功一样多
BD
3.(多选)用回旋加速器对粒子进行加速,可以获得高能带电粒子,两个D形盒与电压有效值为U的高频交流电源的两极相连(频率可调),在两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,磁感应强度为B,如图所示,粒子由速度为零开始加速,不计粒子在两极板间运动的时间,关于回旋加速器的使用,下列说法正确的是( )
A.两盒间狭缝中交变电场的频率跟带电粒子的比荷成正比
B.不同的带电粒子在同一回旋加速器(频率相同)中运动的总时间相同
C.带电粒子在磁场中运动时,受到的洛伦兹力不做功,因此带电粒子从D形盒射出时的动能与磁场的强弱无关
D.尽管两盒间狭缝中电场对带电粒子起加速作用,但是带电粒子从D形盒射出时的动能与加速电压的大小无关
ABD
4.回旋加速器是用来加速带电粒子使它获得很大动能的仪器,其核心部分是两个D形金属盒,两盒分别和一高频交流电源两极相连,以便在盒间的窄缝中形成匀强电场,使粒子每次穿过窄缝都得到加速,两盒放在磁感应强度为B的匀强磁场中,磁场方向垂直于盒底面,粒子源置于盒的圆心附近,若粒子源射出的粒子电荷量为q,质量为m,粒子最大回旋半径为Rm,其运动轨迹如图所示:
(1)盒中有无电场?
(2)粒子在盒内做何种运动?
(3)所加交流电频率应是多大,粒子角速度为多大?
(4)粒子离开加速器时速度是多大,最大动能为多少?
(5)设两D形盒间电场的电势差为U,求加速到上述能量所需的时间.(不计粒子在电场中运动的时间)
二.质谱仪:
测定粒子荷质比的仪器
在磁场中的圆周半径r
洛伦兹力的应用
加速电场
偏转磁场
结构图:
应用:可以测定带电粒子的质量和分析同位素。
1. 如图,从离子源产生的甲、乙两种离子,由静止经加速电压U加速后在纸面内水平向右运动,自M点垂直于磁场边界射入匀强磁场,磁场方向垂直于纸面向里,磁场左边界竖直。已知甲种离子射入磁场的速度大小为v1,并在磁场边界的N点射出;乙种离子在MN的中点射出,MN长为l。不计重力影响和离子间的相互作用。求
(1)磁场的磁感应强度大小;
(2)甲、乙两种离子的比荷之比。
2.(质谱仪)质谱仪测定带电粒子质量的装置示意图如图所示。速度选择器(也称滤速器)中电场强度E的方向竖直向下,磁感应强度B1的方向垂直于纸面向里,分离器中磁感应强度B2的方向垂直于纸面向外。在S处有甲、乙、丙、丁四个一价正离子垂直于E和B1射入速度选择器中,若m甲=m乙A.甲、乙、丙、丁
B.甲、丁、乙、丙
C.丙、丁、乙、甲
D.甲、乙、丁、丙
B
3.其示意图如图所示,其中加速电压恒定.质子在入口处从静止开始被加速电场加速,经匀强磁场偏转后从出口离开磁场.若某种一价正离子在入口处从静止开始被同一加速电场加速,为使它经匀强磁场偏转后仍从同一出口离开磁场,需将磁感应强度增加到原来的12倍.此离子和质子的质量比约为( )
A.11 B.12 C.121 D.144
D
5.如图所示,两平行金属板间距为d,电势差为U,板间电场可视为匀强电场;金属板下方有一磁感应强度为B的匀强磁场。带电量为+q、质量为m的粒子,由静止开始从正极板出发,经电场加速后射出,并进入磁场做匀速圆周运动。忽略重力的影响,求:
(1)粒子进入磁场时的速度;
(2)粒子在磁场中做匀速圆周运动的半径R;
(3)从开始运动到打在极板上所用的时间。
6.如图为质谱仪的示意图.速度选择部分的匀强电场场强E=1.2×105 V/m,匀强磁场的磁感应强度为B1=0.6 T.偏转分离器的磁感应强度为B2=0.8 T.求:
(1)能通过速度选择器的粒子速度有多大?
(2)质子和氘核进入偏转分离器后打在底片上的条纹之间的距离d为多少?(质子的荷质比e/m=108C/kg,氘核荷质比为q/m=0.5×108C/kg)
4.质谱仪与回旋加速器
要认识原子核内部的情况,
必须把核“打开”进行“观察”。
然而原子核被强大的核力约束,
只有用极高能量的粒子作为“炮弹”去轰击,才能把它“打开”。
产生这些高能“炮弹”的“工厂”就是各种各样的粒子加速器。
金属圆筒(漂移管)内场强为零,粒子在圆筒内做匀速直线运动,在圆筒间缝隙做加速运动。
直线加速器
如图所示,直线加速器是使粒子在一条直线装置上被加速.
漂移管
加速缝隙
交流电源
电源为交流电源,当粒子在各筒内穿过的时间都为t=T/2时,粒子才有可能每次通过圆筒间缝隙都被加速.
一台直线加速器“麻雀虽小,五脏俱全”,它包含着一般加速器应具备的几个基本要素:
1.利用电场加速带电粒子;
2.通过多级加速获得高能粒子;
3.将加速电场以外的区域静电屏蔽;
4.采用交变电源提供电压;
5.电压交替变化与带电粒子运动应满足同步条件。
能不能建造一种加速器,在较小的空间范围内让粒子经过多次加速获得所需要的能量呢?
1932年美国科学家劳伦斯发明了回旋加速器,巧妙的应用带电粒子在磁场中运动特点解决了这一问题。
直线加速器的缺点:
体积通常较大,占地面积大。
一. 回旋加速器
1.构造:
运动一周加速两次,v、r变大,但周期不变
3.最大动能:
4.加速次数:
2.原理:
(t与q,m无关)
(由B,Rm决定)
如图,D1、D2是半圆金属盒,D形盒处于匀强磁场中,D形盒的缝隙处接交流电源.
电场使粒子加速(加速过程时间极短,忽略不计),磁场使粒子回旋(匀速圆周运动)
问题1:要让粒子持续加速,T交与T圆满足什么关系?
问题2:粒子运动一周,加速几次?v,r,T如何变?
T交=T圆
f交=f圆
n=Ekm/qU
5.运动总时间:
(n与U有关)
美国物理学家 劳伦斯
1932年,美国物理学家劳伦斯正是沿着与上述相仿的巧妙思路,发明了回旋加速器,从而使人类在获得具有较高能量的粒子方面迈进了一大步。为此,劳伦斯获得了1939年的诺贝尔物理学奖。
1.如图甲所示是用来加速带电粒子的回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,两盒分别与高频交流电源相连。带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示。忽略带电粒子在电场中的加速时间,则下列判断正确的是( )
A.在Ek-t图像中应有t4-t3
C.粒子加速次数越多,粒子最大动能一定越大
D.要想粒子获得的最大动能增大,可增加D形盒的面积
D
2. (多选)1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示。这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙,所加交变电压极性变化时,电压值不变。下列说法正确的是( )
A.所加交变电压的周期等于带电粒子圆周运动周期的一半
B.利用回旋加速器加速带电粒子,要提高加速粒子的最终能量,应尽可能增大磁感应强度B和D形盒的半径R
C.回旋加速器的加速电压越大,带电粒子获得的最大动能越大
D.粒子每次经过D形盒狭缝时,电场力对粒子做功一样多
BD
3.(多选)用回旋加速器对粒子进行加速,可以获得高能带电粒子,两个D形盒与电压有效值为U的高频交流电源的两极相连(频率可调),在两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,磁感应强度为B,如图所示,粒子由速度为零开始加速,不计粒子在两极板间运动的时间,关于回旋加速器的使用,下列说法正确的是( )
A.两盒间狭缝中交变电场的频率跟带电粒子的比荷成正比
B.不同的带电粒子在同一回旋加速器(频率相同)中运动的总时间相同
C.带电粒子在磁场中运动时,受到的洛伦兹力不做功,因此带电粒子从D形盒射出时的动能与磁场的强弱无关
D.尽管两盒间狭缝中电场对带电粒子起加速作用,但是带电粒子从D形盒射出时的动能与加速电压的大小无关
ABD
4.回旋加速器是用来加速带电粒子使它获得很大动能的仪器,其核心部分是两个D形金属盒,两盒分别和一高频交流电源两极相连,以便在盒间的窄缝中形成匀强电场,使粒子每次穿过窄缝都得到加速,两盒放在磁感应强度为B的匀强磁场中,磁场方向垂直于盒底面,粒子源置于盒的圆心附近,若粒子源射出的粒子电荷量为q,质量为m,粒子最大回旋半径为Rm,其运动轨迹如图所示:
(1)盒中有无电场?
(2)粒子在盒内做何种运动?
(3)所加交流电频率应是多大,粒子角速度为多大?
(4)粒子离开加速器时速度是多大,最大动能为多少?
(5)设两D形盒间电场的电势差为U,求加速到上述能量所需的时间.(不计粒子在电场中运动的时间)
二.质谱仪:
测定粒子荷质比的仪器
在磁场中的圆周半径r
洛伦兹力的应用
加速电场
偏转磁场
结构图:
应用:可以测定带电粒子的质量和分析同位素。
1. 如图,从离子源产生的甲、乙两种离子,由静止经加速电压U加速后在纸面内水平向右运动,自M点垂直于磁场边界射入匀强磁场,磁场方向垂直于纸面向里,磁场左边界竖直。已知甲种离子射入磁场的速度大小为v1,并在磁场边界的N点射出;乙种离子在MN的中点射出,MN长为l。不计重力影响和离子间的相互作用。求
(1)磁场的磁感应强度大小;
(2)甲、乙两种离子的比荷之比。
2.(质谱仪)质谱仪测定带电粒子质量的装置示意图如图所示。速度选择器(也称滤速器)中电场强度E的方向竖直向下,磁感应强度B1的方向垂直于纸面向里,分离器中磁感应强度B2的方向垂直于纸面向外。在S处有甲、乙、丙、丁四个一价正离子垂直于E和B1射入速度选择器中,若m甲=m乙
B.甲、丁、乙、丙
C.丙、丁、乙、甲
D.甲、乙、丁、丙
B
3.其示意图如图所示,其中加速电压恒定.质子在入口处从静止开始被加速电场加速,经匀强磁场偏转后从出口离开磁场.若某种一价正离子在入口处从静止开始被同一加速电场加速,为使它经匀强磁场偏转后仍从同一出口离开磁场,需将磁感应强度增加到原来的12倍.此离子和质子的质量比约为( )
A.11 B.12 C.121 D.144
D
5.如图所示,两平行金属板间距为d,电势差为U,板间电场可视为匀强电场;金属板下方有一磁感应强度为B的匀强磁场。带电量为+q、质量为m的粒子,由静止开始从正极板出发,经电场加速后射出,并进入磁场做匀速圆周运动。忽略重力的影响,求:
(1)粒子进入磁场时的速度;
(2)粒子在磁场中做匀速圆周运动的半径R;
(3)从开始运动到打在极板上所用的时间。
6.如图为质谱仪的示意图.速度选择部分的匀强电场场强E=1.2×105 V/m,匀强磁场的磁感应强度为B1=0.6 T.偏转分离器的磁感应强度为B2=0.8 T.求:
(1)能通过速度选择器的粒子速度有多大?
(2)质子和氘核进入偏转分离器后打在底片上的条纹之间的距离d为多少?(质子的荷质比e/m=108C/kg,氘核荷质比为q/m=0.5×108C/kg)
