11.3 多边形及其内角和 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 11.3 多边形及其内角和 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 218.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 19:46:42 | ||
图片预览



文档简介
11.3 多边形及其内角和
任务一 利用内、外角和公式求边数
子任务1 已知正多边形的内角度数,求边数
母题1 若一个多边形的每个内角都是108°,则这个多边形的边数为 ( )
A.4 B.5 C.6 D.8
变式练1:若一个正n边形的每个外角为36°,则这个正n边形的边数是 ( )
A.10 B.11 C.12 D.14
子任务2 已知多边形的内角和,求边数
母题2 已知两个多边形的内角和为2160°,且边数之比为1∶3,求这两个多边形的边数.
【关键点拨】
变式练2:若n边形的内角和是五边形的外角和的3倍,则n的值为 ( )
A.6 B.7 C.8 D.9
子任务3 已知多边形的内角和与外角和的关系,求边数
母题3 (1)已知一个多边形的内角和是它的外角和的3倍,求这个多边形的边数.
(2)已知一个多边形的内角和比外角和多540°,问它是几边形
变式练3:一个多边形的内角和与它的外角和的比为5∶2,则这个多边形的边数为 ( )
A.8 B.7 C.6 D.5
任务二 利用内、外角和公式求角度
子任务1 求多边形的外角的度数
母题4 已知一个正多边形的内角和为1440°,则这个正多边形的每一个外角的度数是 ( )
A.36° B.45° C.72° D.60°
【关键点拨】
变式练4:已知正多边形的一个内角等于一个外角的3倍,那么这个正多边形的边数为 ( )
A.6 B.7 C.8 D.9
子任务2 求多边形的内角的度数
母题5 若一个多边形除一个内角外,其余内角的和为1510°,则这个多边形的边数是 ,这个内角的度数是 .
变式练5:小明在计算一个多边形的内角和时,漏掉了一个内角,结果算得800°,则这个多边形应该是 ( )
A.六边形 B.七边形
C.八边形 D.九边形
子任务3 求两个角的和
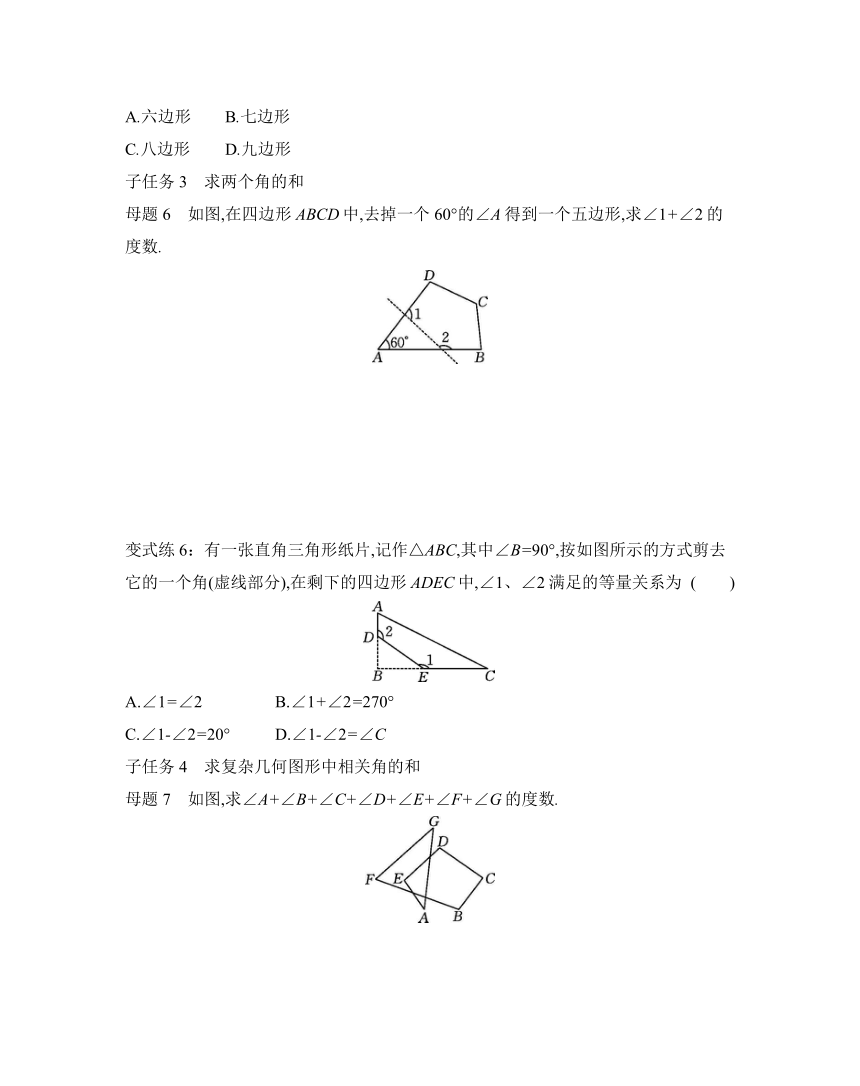
母题6 如图,在四边形ABCD中,去掉一个60°的∠A得到一个五边形,求∠1+∠2的度数.
变式练6:有一张直角三角形纸片,记作△ABC,其中∠B=90°,按如图所示的方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,∠1、∠2满足的等量关系为 ( )
A.∠1=∠2 B.∠1+∠2=270°
C.∠1-∠2=20° D.∠1-∠2=∠C
子任务4 求复杂几何图形中相关角的和
母题7 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
【关键点拨】
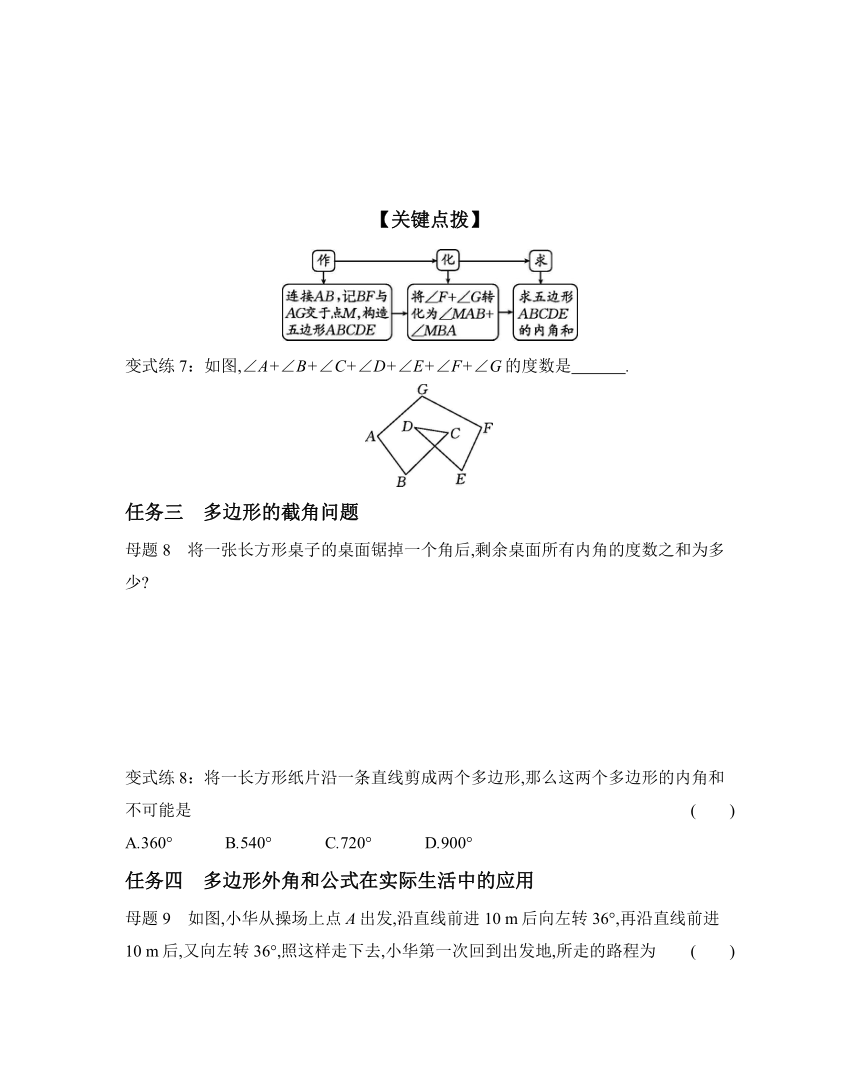
变式练7:如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数是 .
任务三 多边形的截角问题
母题8 将一张长方形桌子的桌面锯掉一个角后,剩余桌面所有内角的度数之和为多少
变式练8:将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和不可能是 ( )
A.360° B.540° C.720° D.900°
任务四 多边形外角和公式在实际生活中的应用
母题9 如图,小华从操场上点A出发,沿直线前进10 m后向左转36°,再沿直线前进10 m后,又向左转36°,照这样走下去,小华第一次回到出发地,所走的路程为 ( )
A.80 m B.90 m
C.100 m D.110 m
变式练9:如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α的度数为 ( )
A.30° B.40° C.80° D.108°
任务五 与多边形有关的探究性问题
母题10 在四边形ABCD中,∠BAD的平分线与边BC交于点E,∠ADC的平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
①如图1,若∠B=40°,∠C=70°,则∠DOE= °;
②如图2,试探索∠B,∠C,∠DOE之间的数量关系,并说明理由.
(2)如图3,若点O在四边形ABCD的外部,请你直接写出∠B,∠C,∠DOE之间的数量关系.
变式练10:已知在四边形ABCD中,∠A=x,∠C=y(0°(1)∠ABC+∠ADC= .(用含x,y的式子表示)
(2)如图1,若x=y=90°,DE平分∠ADC,BF平分与∠ABC相邻的外角,请写出DE与BF的位置关系,并说明理由.
(3)如图2,∠DFB为四边形ABCD的∠ABC,∠ADC相邻的外角平分线所在直线构成的锐角.
①当x②小明在作图时,发现∠DFB不一定存在,请直接指出x,y满足什么条件时,∠DFB不存在.
参考答案
母题1 B 提示:外角的度数是180-108=72°,
则这个多边形的边数是360÷72=5.
故选B.
变式练1 A 提示:一个正n边形的每个外角为36°.
所以这个正n边形的边数为360°÷36°=10.
故选A.
母题2 解:设这两个多边形的边数分别是x和3x,
则(x-2)·180°+(3x-2)·180°=2160°,
解得x=4,
则这两个多边形的边数分别为4和12.
变式练2 C 提示:∵一个n边形的内角和是五边形外角和的3倍,
∴180°×(n-2)=360°×3,
解得n=8.
故选C.
母题3 解:(1)设这个多边形的边数为n.
∵n边形的内角和为(n-2)·180°,多边形的外角和为360°,
∴(n-2)·180°=360°×3,
解得n=8,
∴这个多边形的边数为8.
(2)设这个多边形的边数为n,
则其内角和为(n-2)·180°.
∵这个n边形的外角和为360°,内角和比外角和多540°,
∴(n-2)×180°-360°=540°,
解得n=7,
∴这个多边形是七边形.
变式练3 B 提示:设多边形的边数是n,则
(n-2)·180°∶360°=5∶2,
整理得n-2=5,
解得n=7.
故选B.
母题4 A 提示:设此多边形为n边形,
根据题意得180(n-2)=1440,
解得n=10,
故这个正多边形的每一个外角等于360°÷10=36°.
故选A.
变式练4 C 提示:设这个正多边形的一个外角的度数为x,则其一个内角的度数为3x,
所以x+3x=180°,x=45°,
则该正多边形的边数是360°÷45°=8.
故选C.
母题5 11;110° 提示:设多边形有n条边,根据多边形内角和定理,得0°<180°×(n-2)-1510°<180°,
解得10.39由边数为正整数,得n=11,
∴(11-2)×180°-1510°=1620°-1510°=110°,
故这个多边形的边数为11,这个内角的度数是110°.
变式练5 B 提示:设多边形的边数是n.
依题意有0°<(n-2)·180°-800°<180°,
解得6则多边形的边数n=7.
故选B.
母题6 解:∵四边形的内角和为(4-2)×180°=360°,∠A=60°,
∴∠B+∠C+∠D=360°-60°=300°.
∵五边形的内角和为(5-2)×180°=540°,
∴∠1+∠2=540°-300°=240°.
变式练6 B 提示:∵∠B=90°,
∴∠BDE+∠BED=90°,
∴∠1+∠2=180°+180°-90°=270°.
故选B.
母题7 解:如图,连接AB,设BF与AG交于点M.
∵∠F+∠G+∠FMG=180°,∠GAB+∠FBA+∠AMB=180°,
∴∠F+∠G+∠FMG=∠GAB+∠FBA+∠AMB.
∵∠FMG=∠AMB,
∴∠F+∠G=∠GAB+∠FBA,
∴∠GAE+∠FBC+∠C+∠D+∠E+∠F+∠G
=∠GAE+∠FBC+∠C+∠D+∠E+∠GAB+∠FBA
=180°×(5-2)
=540°.
变式练7 540° 提示:连接BE,如图所示.
在△CDM与△BEM中,∠CMD=∠BME,
∴∠C+∠D=∠CBE+∠DEB,
∴在五边形ABEFG中,∠A+∠ABC+∠C+∠D+∠DEF+∠F+∠G
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F+∠G
=∠A+∠ABE+∠BEF+∠F+∠G
=(5-2)×180°
=540°.
母题8 解:长方形的桌子据掉一个角以后可能是三角形或四边形或五边形,即还剩下3或4或5个角,
180°×(3-2)=180°,180°×(4-2)=360°,180°×(5-2)=540°,
故这些角的度数之和可能是180°或360°或540°.
变式练8 D 提示:①将长方形沿对角线剪开,得到两个三角形,则两个多边形的内角和为180°+180°=360°;
②将长方形从一顶点剪向对边,得到一个三角形和一个四边形,则两个多边形的内角和为180°+360°=540°;
③将长方形沿一组对边剪开,得到两个四边形,则两个多边形的内角和为360°+360°=720°;
④将长方形沿一组邻边剪开,得到一个三角形和一个五边形,则两个多边形的内角和为180°+540°=720°.
故选D.
母题9 C 提示:360°÷36°=10,
10×10=100 m.
故选C.
变式练9 B 提示:设路线形成的多边形的边数为n,根据题意,
n=108÷12=9,
则α=360°÷9=40°.
故选B.
母题10 解:(1)①125.
②∠B+∠C+2∠DOE=360°.
理由:∵∠DOE=∠OAD+∠ADO,AE,DO分别平分∠BAD,∠CDA,
∴2∠DOE=∠BAD+∠ADC.
∵∠B+∠C+∠BAD+∠ADC=360°,
∴∠B+∠C+2∠DOE=360°.
(2)∠B+∠C=2∠DOE.
提示:∵∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,AE,DO分别平分∠BAD,∠CDA,
∴∠BAD=2∠EAD,∠ADC=2∠ADO,
∴∠BAD+∠ADC=2(∠EAD+∠ADO),
∴360°-∠B-∠C=2(180°-∠DOE),
∴∠B+∠C=2∠DOE.
变式练10 解:(1)360°-x-y.
(2)DE⊥BF.
理由:如图1,延长DE交BF于点G.
由(1)知∠ABC+∠ADC=360°-(∠A+∠C)=360°-x-y.
∴当x=y=90°时,∠ABC+∠ADC=180°.
∵DE平分∠ADC,∴∠CDE=∠ADC.
又∵∠C=90°,∴∠EDC+∠DEC=180°-∠C=90°,
∴∠DEC=90°-∠EDC=90°-∠ADC.
又∵∠BEG与∠DEC是对顶角,
∴∠BEG=∠DEC=90°-∠ADC.
∵BF平分∠CBM,∴∠EBG=∠EBM.
又∵∠ABC+∠EBM=180°,∴∠EBM=180°-∠ABC,
∴∠EBG=90°-∠ABC,
∴∠EBG+∠BEG=90°-∠ABC+90°-∠ADC
=180°-(∠ADC+∠ABC)=90°,
∴∠EGB=180°-(∠EBG+∠BEG)=90°,∴DE⊥BF.
(3)①如图2,连接FC并延长至点G.
∵x+y=140°,
∴∠ABC+∠ADC=360°-(∠A+∠DCB)=360°-x-y=220°.
∵DF平分∠NDC,
∴∠FDC=∠NDC = (180°-∠ADC)= 90°-∠ADC.
同理可证∠FBC=90°-∠ABC.
∵∠DCG=∠CDF+∠DFC,∠GCB=∠CBF+∠CFB,
∴∠DCB=∠DCG+∠GCB=∠CDF+∠CBF+∠DFB=90°-∠ADC+90°-∠ABC+30°=210°-(∠ADC+∠ABC)=100°,
∴y=100°,∴x=40°.
②当0
任务一 利用内、外角和公式求边数
子任务1 已知正多边形的内角度数,求边数
母题1 若一个多边形的每个内角都是108°,则这个多边形的边数为 ( )
A.4 B.5 C.6 D.8
变式练1:若一个正n边形的每个外角为36°,则这个正n边形的边数是 ( )
A.10 B.11 C.12 D.14
子任务2 已知多边形的内角和,求边数
母题2 已知两个多边形的内角和为2160°,且边数之比为1∶3,求这两个多边形的边数.
【关键点拨】
变式练2:若n边形的内角和是五边形的外角和的3倍,则n的值为 ( )
A.6 B.7 C.8 D.9
子任务3 已知多边形的内角和与外角和的关系,求边数
母题3 (1)已知一个多边形的内角和是它的外角和的3倍,求这个多边形的边数.
(2)已知一个多边形的内角和比外角和多540°,问它是几边形
变式练3:一个多边形的内角和与它的外角和的比为5∶2,则这个多边形的边数为 ( )
A.8 B.7 C.6 D.5
任务二 利用内、外角和公式求角度
子任务1 求多边形的外角的度数
母题4 已知一个正多边形的内角和为1440°,则这个正多边形的每一个外角的度数是 ( )
A.36° B.45° C.72° D.60°
【关键点拨】
变式练4:已知正多边形的一个内角等于一个外角的3倍,那么这个正多边形的边数为 ( )
A.6 B.7 C.8 D.9
子任务2 求多边形的内角的度数
母题5 若一个多边形除一个内角外,其余内角的和为1510°,则这个多边形的边数是 ,这个内角的度数是 .
变式练5:小明在计算一个多边形的内角和时,漏掉了一个内角,结果算得800°,则这个多边形应该是 ( )
A.六边形 B.七边形
C.八边形 D.九边形
子任务3 求两个角的和
母题6 如图,在四边形ABCD中,去掉一个60°的∠A得到一个五边形,求∠1+∠2的度数.
变式练6:有一张直角三角形纸片,记作△ABC,其中∠B=90°,按如图所示的方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,∠1、∠2满足的等量关系为 ( )
A.∠1=∠2 B.∠1+∠2=270°
C.∠1-∠2=20° D.∠1-∠2=∠C
子任务4 求复杂几何图形中相关角的和
母题7 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
【关键点拨】
变式练7:如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数是 .
任务三 多边形的截角问题
母题8 将一张长方形桌子的桌面锯掉一个角后,剩余桌面所有内角的度数之和为多少
变式练8:将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和不可能是 ( )
A.360° B.540° C.720° D.900°
任务四 多边形外角和公式在实际生活中的应用
母题9 如图,小华从操场上点A出发,沿直线前进10 m后向左转36°,再沿直线前进10 m后,又向左转36°,照这样走下去,小华第一次回到出发地,所走的路程为 ( )
A.80 m B.90 m
C.100 m D.110 m
变式练9:如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α的度数为 ( )
A.30° B.40° C.80° D.108°
任务五 与多边形有关的探究性问题
母题10 在四边形ABCD中,∠BAD的平分线与边BC交于点E,∠ADC的平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
①如图1,若∠B=40°,∠C=70°,则∠DOE= °;
②如图2,试探索∠B,∠C,∠DOE之间的数量关系,并说明理由.
(2)如图3,若点O在四边形ABCD的外部,请你直接写出∠B,∠C,∠DOE之间的数量关系.
变式练10:已知在四边形ABCD中,∠A=x,∠C=y(0°
(2)如图1,若x=y=90°,DE平分∠ADC,BF平分与∠ABC相邻的外角,请写出DE与BF的位置关系,并说明理由.
(3)如图2,∠DFB为四边形ABCD的∠ABC,∠ADC相邻的外角平分线所在直线构成的锐角.
①当x
参考答案
母题1 B 提示:外角的度数是180-108=72°,
则这个多边形的边数是360÷72=5.
故选B.
变式练1 A 提示:一个正n边形的每个外角为36°.
所以这个正n边形的边数为360°÷36°=10.
故选A.
母题2 解:设这两个多边形的边数分别是x和3x,
则(x-2)·180°+(3x-2)·180°=2160°,
解得x=4,
则这两个多边形的边数分别为4和12.
变式练2 C 提示:∵一个n边形的内角和是五边形外角和的3倍,
∴180°×(n-2)=360°×3,
解得n=8.
故选C.
母题3 解:(1)设这个多边形的边数为n.
∵n边形的内角和为(n-2)·180°,多边形的外角和为360°,
∴(n-2)·180°=360°×3,
解得n=8,
∴这个多边形的边数为8.
(2)设这个多边形的边数为n,
则其内角和为(n-2)·180°.
∵这个n边形的外角和为360°,内角和比外角和多540°,
∴(n-2)×180°-360°=540°,
解得n=7,
∴这个多边形是七边形.
变式练3 B 提示:设多边形的边数是n,则
(n-2)·180°∶360°=5∶2,
整理得n-2=5,
解得n=7.
故选B.
母题4 A 提示:设此多边形为n边形,
根据题意得180(n-2)=1440,
解得n=10,
故这个正多边形的每一个外角等于360°÷10=36°.
故选A.
变式练4 C 提示:设这个正多边形的一个外角的度数为x,则其一个内角的度数为3x,
所以x+3x=180°,x=45°,
则该正多边形的边数是360°÷45°=8.
故选C.
母题5 11;110° 提示:设多边形有n条边,根据多边形内角和定理,得0°<180°×(n-2)-1510°<180°,
解得10.39
∴(11-2)×180°-1510°=1620°-1510°=110°,
故这个多边形的边数为11,这个内角的度数是110°.
变式练5 B 提示:设多边形的边数是n.
依题意有0°<(n-2)·180°-800°<180°,
解得6
故选B.
母题6 解:∵四边形的内角和为(4-2)×180°=360°,∠A=60°,
∴∠B+∠C+∠D=360°-60°=300°.
∵五边形的内角和为(5-2)×180°=540°,
∴∠1+∠2=540°-300°=240°.
变式练6 B 提示:∵∠B=90°,
∴∠BDE+∠BED=90°,
∴∠1+∠2=180°+180°-90°=270°.
故选B.
母题7 解:如图,连接AB,设BF与AG交于点M.
∵∠F+∠G+∠FMG=180°,∠GAB+∠FBA+∠AMB=180°,
∴∠F+∠G+∠FMG=∠GAB+∠FBA+∠AMB.
∵∠FMG=∠AMB,
∴∠F+∠G=∠GAB+∠FBA,
∴∠GAE+∠FBC+∠C+∠D+∠E+∠F+∠G
=∠GAE+∠FBC+∠C+∠D+∠E+∠GAB+∠FBA
=180°×(5-2)
=540°.
变式练7 540° 提示:连接BE,如图所示.
在△CDM与△BEM中,∠CMD=∠BME,
∴∠C+∠D=∠CBE+∠DEB,
∴在五边形ABEFG中,∠A+∠ABC+∠C+∠D+∠DEF+∠F+∠G
=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F+∠G
=∠A+∠ABE+∠BEF+∠F+∠G
=(5-2)×180°
=540°.
母题8 解:长方形的桌子据掉一个角以后可能是三角形或四边形或五边形,即还剩下3或4或5个角,
180°×(3-2)=180°,180°×(4-2)=360°,180°×(5-2)=540°,
故这些角的度数之和可能是180°或360°或540°.
变式练8 D 提示:①将长方形沿对角线剪开,得到两个三角形,则两个多边形的内角和为180°+180°=360°;
②将长方形从一顶点剪向对边,得到一个三角形和一个四边形,则两个多边形的内角和为180°+360°=540°;
③将长方形沿一组对边剪开,得到两个四边形,则两个多边形的内角和为360°+360°=720°;
④将长方形沿一组邻边剪开,得到一个三角形和一个五边形,则两个多边形的内角和为180°+540°=720°.
故选D.
母题9 C 提示:360°÷36°=10,
10×10=100 m.
故选C.
变式练9 B 提示:设路线形成的多边形的边数为n,根据题意,
n=108÷12=9,
则α=360°÷9=40°.
故选B.
母题10 解:(1)①125.
②∠B+∠C+2∠DOE=360°.
理由:∵∠DOE=∠OAD+∠ADO,AE,DO分别平分∠BAD,∠CDA,
∴2∠DOE=∠BAD+∠ADC.
∵∠B+∠C+∠BAD+∠ADC=360°,
∴∠B+∠C+2∠DOE=360°.
(2)∠B+∠C=2∠DOE.
提示:∵∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,AE,DO分别平分∠BAD,∠CDA,
∴∠BAD=2∠EAD,∠ADC=2∠ADO,
∴∠BAD+∠ADC=2(∠EAD+∠ADO),
∴360°-∠B-∠C=2(180°-∠DOE),
∴∠B+∠C=2∠DOE.
变式练10 解:(1)360°-x-y.
(2)DE⊥BF.
理由:如图1,延长DE交BF于点G.
由(1)知∠ABC+∠ADC=360°-(∠A+∠C)=360°-x-y.
∴当x=y=90°时,∠ABC+∠ADC=180°.
∵DE平分∠ADC,∴∠CDE=∠ADC.
又∵∠C=90°,∴∠EDC+∠DEC=180°-∠C=90°,
∴∠DEC=90°-∠EDC=90°-∠ADC.
又∵∠BEG与∠DEC是对顶角,
∴∠BEG=∠DEC=90°-∠ADC.
∵BF平分∠CBM,∴∠EBG=∠EBM.
又∵∠ABC+∠EBM=180°,∴∠EBM=180°-∠ABC,
∴∠EBG=90°-∠ABC,
∴∠EBG+∠BEG=90°-∠ABC+90°-∠ADC
=180°-(∠ADC+∠ABC)=90°,
∴∠EGB=180°-(∠EBG+∠BEG)=90°,∴DE⊥BF.
(3)①如图2,连接FC并延长至点G.
∵x+y=140°,
∴∠ABC+∠ADC=360°-(∠A+∠DCB)=360°-x-y=220°.
∵DF平分∠NDC,
∴∠FDC=∠NDC = (180°-∠ADC)= 90°-∠ADC.
同理可证∠FBC=90°-∠ABC.
∵∠DCG=∠CDF+∠DFC,∠GCB=∠CBF+∠CFB,
∴∠DCB=∠DCG+∠GCB=∠CDF+∠CBF+∠DFB=90°-∠ADC+90°-∠ABC+30°=210°-(∠ADC+∠ABC)=100°,
∴y=100°,∴x=40°.
②当0
