12.1 全等三角形 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 12.1 全等三角形 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 192.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 19:47:08 | ||
图片预览


文档简介
12.1 全等三角形
任务一 利用全等三角形的性质进行计算
子任务1 利用全等三角形的性质求角度
母题1 如图,△ABE≌△ACD,∠A=60°,∠B=25°,求∠BOC的度数.
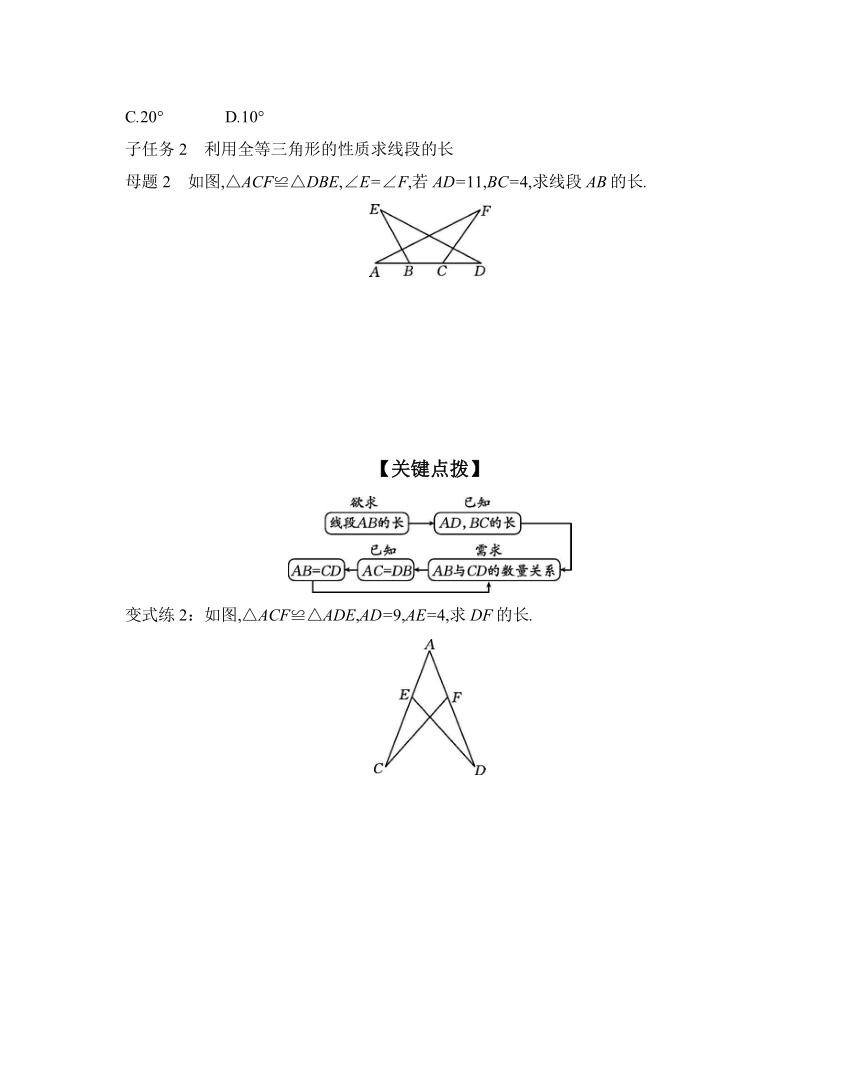
变式练1:如图,△ABC≌△A1B1C,若∠A=50°,∠A1B1C=45°,∠ACB1=65°,则∠α的度数是 ( )
A.15° B.25°
C.20° D.10°
子任务2 利用全等三角形的性质求线段的长
母题2 如图,△ACF≌△DBE,∠E=∠F,若AD=11,BC=4,求线段AB的长.
【关键点拨】
变式练2:如图,△ACF≌△ADE,AD=9,AE=4,求DF的长.
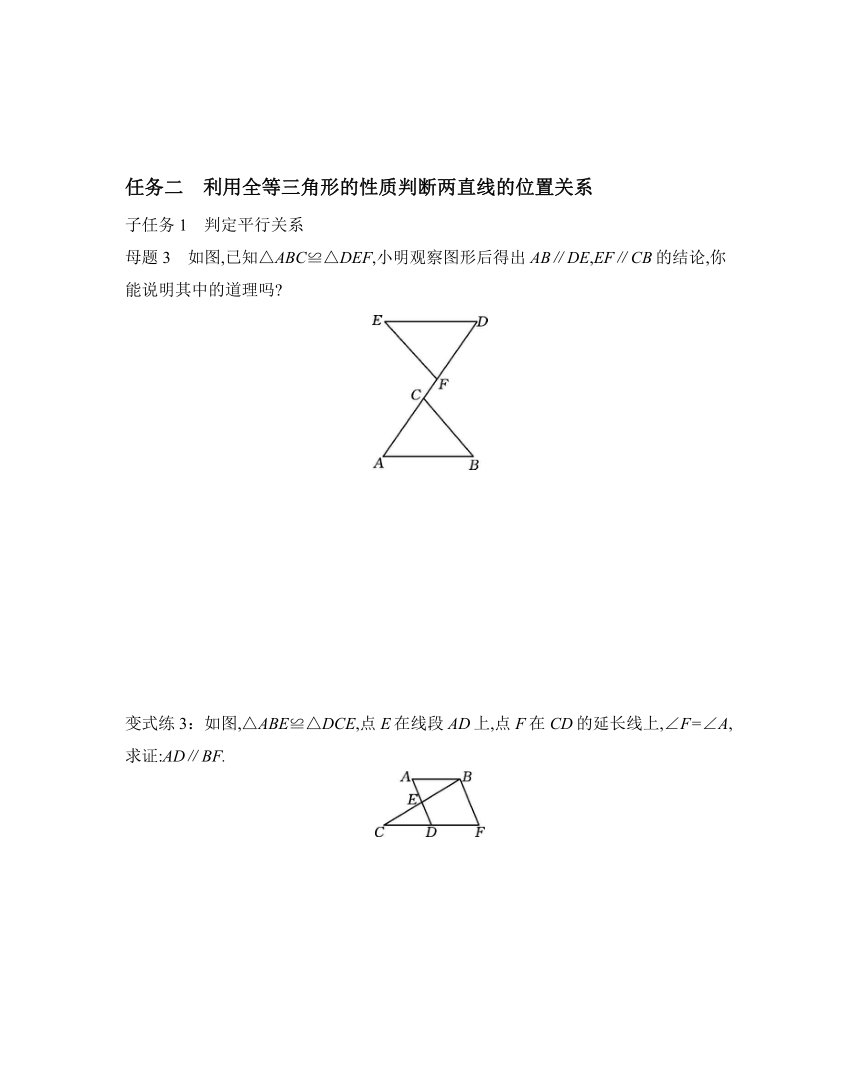
任务二 利用全等三角形的性质判断两直线的位置关系
子任务1 判定平行关系
母题3 如图,已知△ABC≌△DEF,小明观察图形后得出AB∥DE,EF∥CB的结论,你能说明其中的道理吗
变式练3:如图,△ABE≌△DCE,点E在线段AD上,点F在CD的延长线上,∠F=∠A,求证:AD∥BF.
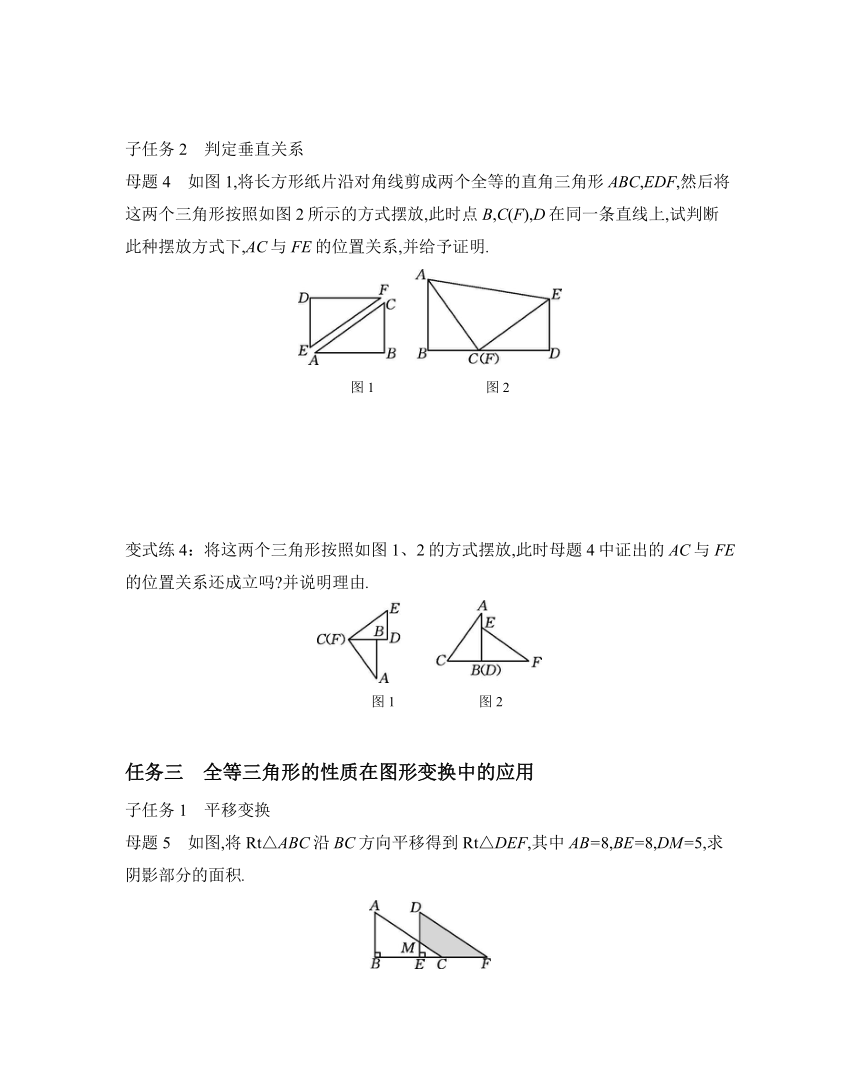
子任务2 判定垂直关系
母题4 如图1,将长方形纸片沿对角线剪成两个全等的直角三角形ABC,EDF,然后将这两个三角形按照如图2所示的方式摆放,此时点B,C(F),D在同一条直线上,试判断此种摆放方式下,AC与FE的位置关系,并给予证明.
图1 图2
变式练4:将这两个三角形按照如图1、2的方式摆放,此时母题4中证出的AC与FE的位置关系还成立吗 并说明理由.
图1 图2
任务三 全等三角形的性质在图形变换中的应用
子任务1 平移变换
母题5 如图,将Rt△ABC沿BC方向平移得到Rt△DEF,其中AB=8,BE=8,DM=5,求阴影部分的面积.
【关键点拨】
变式练5:如图,将△ABC沿BC方向平移到△DEF的位置,∠B=85°,∠A=60°,AB=5,AC与DE交于点H,EH=3.
(1)求∠F的度数与DH的长.
(2)求证:AC∥DF.
子任务2 旋转变换
母题6 如图,将△ABC绕点A旋转至△ADE的位置,使点E落在BC边上,有以下结论:①DE=BC;②∠EAC=∠DAB;③EA平分∠DEC;④若DE∥AC,则∠DEB=60°.其中正确结论的个数是 ( )
A.4 B.3 C.2 D.1
变式练6:三个全等三角形按如图所示的形式摆放,则∠1+∠2+∠3的度数等于 .
子任务3 翻折变换
母题7 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F处,如果∠BAF=60°,那么∠DAE等于 ( )
A.60° B.45° C.30° D.15°
变式练7:如图,在三角形纸片ABC中,AB=10 cm,BC=7 cm,AC=6 cm.沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
A.13 cm B.9 cm
C.16 cm D.10 cm
参考答案
母题1 解:∵∠A=60°,∠B=25°,
∴∠CEO=∠A+∠B=85°.
∵△ABE≌△ACD,
∴∠B=∠C=25°,
∴∠BOC=∠C+∠CEO=110°.
变式练1 C 提示:∵△ABC≌△A1B1C,∠A1B1C=45°,
∴∠ABC=∠A1B1C=45°.
∵∠A=50°,
∴∠ACB=180°-∠ABC-∠A=85°.
∵∠ACB1=65°,
∴∠α=∠ACB-∠ACB1=85°-65°=20°.
故选C.
母题2 解:∵△ACF≌△DBE,
∴AC=DB,
∴AC-BC=DB-BC,
即AB=CD.
∵AD=11,BC=4,
∴AB=(AD-BC)=×(11-4)=3.5,
即AB=3.5.
变式练2 解:∵△ACF≌△ADE,
∴AE=AF,AD=AC,
∴AD-AF=AD-AE,
∴DF=AD-AF=AD-AE=9-4=5.
母题3 证明:∵△ABC≌△DEF,
∴∠A=∠D,∠ACB=∠DFE,
∴∠BCF=∠EFA,
∴EF∥CB.
∵∠D=∠A,
∴ED∥AB.
变式练3 证明:∵△ABE≌△DCE,
∴∠A=∠ADC.
∵∠F=∠A,
∴∠F=∠ADC,
∴AD∥BF.
母题4 解:AC⊥FE.
证明:如题图2,由题意知,Rt△ABC≌Rt△CDE,
∴∠BAC=∠DCE.
在Rt△ABC中,∵∠BAC+∠ACB=90°,
∴∠DCE+∠ACB=90°,
∴∠ACE=180°-(∠DCE+∠ACB)=180°-90°=90°,∴AC⊥FE.
变式练4 解:成立,证明略.
母题5 解:∵直角△ABC沿BC方向平移得到直角△DEF,
∴DE=AB=8.
∵DM=5,
∴ME=DE-DM=8-5=3.
由平移可得
S阴影=S△DEF-S△MEC
=S△ABC-S△MEC
=S梯形ABEM
=×(3+8)×8,
=44.
变式练5 解:(1)∵将△ABC沿BC方向平移到△DEF的位置,
∴△ABC≌△DEF,
∴AB=DE=5,∠DEF=∠B=85°,
∠D=∠A=60°,
∴∠F=180°-∠D-∠DEF=35°.
∵EH=3,∴DH=DE-EH=2.
(2)证明:∵△ABC≌△DEF,
∴∠ACB=∠F,
∴AC∥DF.
母题6 A 提示:由旋转的性质可知,△ABC≌△ADE,
∴DE=BC,∠BAC=∠DAE,
∴∠CAE=∠CAB-∠BAE,∠DAB=∠DAE-∠BAE,
∴∠EAC=∠DAB.
∵AE=AC,
∴∠AEC=∠C.
∵∠C=∠AED,
∴∠AEC=∠AED,
∴EA平分∠DEC.
∵DE∥AC,
∴∠C=∠BED.
∵∠AEC=∠AED=∠C,
∴∠DEB=60°.
故选A.
变式练6 180° 提示:如图所示.
由图形可得∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°.
∵三个三角形全等,
∴∠4+∠9+∠6=180°.
又∵∠5+∠7+∠8=180°.
∴∠1+∠2+∠3+180°+180°=540°,
∴∠1+∠2+∠3的度数是180°.
母题7 D 提示:∵将长方形ABCD沿AE折叠,使点D落在BC边上的点F处,
∴∠DAE=∠EAF.
∵∠BAF=60°,
∴∠DAE=∠EAF=∠DAF=×(90°-60°)=15°.
故选D.
变式练7 B 提示:∵折叠后这个三角形的顶点C落在AB边上的点E处,
∴DE=CD,BE=BC=7 cm,
∴AE=AB-BE=10-7=3(cm).
∵AD+DE=AD+CD=AC=6 cm,
∴△AED的周长=6+3=9(cm).
故选B.
任务一 利用全等三角形的性质进行计算
子任务1 利用全等三角形的性质求角度
母题1 如图,△ABE≌△ACD,∠A=60°,∠B=25°,求∠BOC的度数.
变式练1:如图,△ABC≌△A1B1C,若∠A=50°,∠A1B1C=45°,∠ACB1=65°,则∠α的度数是 ( )
A.15° B.25°
C.20° D.10°
子任务2 利用全等三角形的性质求线段的长
母题2 如图,△ACF≌△DBE,∠E=∠F,若AD=11,BC=4,求线段AB的长.
【关键点拨】
变式练2:如图,△ACF≌△ADE,AD=9,AE=4,求DF的长.
任务二 利用全等三角形的性质判断两直线的位置关系
子任务1 判定平行关系
母题3 如图,已知△ABC≌△DEF,小明观察图形后得出AB∥DE,EF∥CB的结论,你能说明其中的道理吗
变式练3:如图,△ABE≌△DCE,点E在线段AD上,点F在CD的延长线上,∠F=∠A,求证:AD∥BF.
子任务2 判定垂直关系
母题4 如图1,将长方形纸片沿对角线剪成两个全等的直角三角形ABC,EDF,然后将这两个三角形按照如图2所示的方式摆放,此时点B,C(F),D在同一条直线上,试判断此种摆放方式下,AC与FE的位置关系,并给予证明.
图1 图2
变式练4:将这两个三角形按照如图1、2的方式摆放,此时母题4中证出的AC与FE的位置关系还成立吗 并说明理由.
图1 图2
任务三 全等三角形的性质在图形变换中的应用
子任务1 平移变换
母题5 如图,将Rt△ABC沿BC方向平移得到Rt△DEF,其中AB=8,BE=8,DM=5,求阴影部分的面积.
【关键点拨】
变式练5:如图,将△ABC沿BC方向平移到△DEF的位置,∠B=85°,∠A=60°,AB=5,AC与DE交于点H,EH=3.
(1)求∠F的度数与DH的长.
(2)求证:AC∥DF.
子任务2 旋转变换
母题6 如图,将△ABC绕点A旋转至△ADE的位置,使点E落在BC边上,有以下结论:①DE=BC;②∠EAC=∠DAB;③EA平分∠DEC;④若DE∥AC,则∠DEB=60°.其中正确结论的个数是 ( )
A.4 B.3 C.2 D.1
变式练6:三个全等三角形按如图所示的形式摆放,则∠1+∠2+∠3的度数等于 .
子任务3 翻折变换
母题7 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F处,如果∠BAF=60°,那么∠DAE等于 ( )
A.60° B.45° C.30° D.15°
变式练7:如图,在三角形纸片ABC中,AB=10 cm,BC=7 cm,AC=6 cm.沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
A.13 cm B.9 cm
C.16 cm D.10 cm
参考答案
母题1 解:∵∠A=60°,∠B=25°,
∴∠CEO=∠A+∠B=85°.
∵△ABE≌△ACD,
∴∠B=∠C=25°,
∴∠BOC=∠C+∠CEO=110°.
变式练1 C 提示:∵△ABC≌△A1B1C,∠A1B1C=45°,
∴∠ABC=∠A1B1C=45°.
∵∠A=50°,
∴∠ACB=180°-∠ABC-∠A=85°.
∵∠ACB1=65°,
∴∠α=∠ACB-∠ACB1=85°-65°=20°.
故选C.
母题2 解:∵△ACF≌△DBE,
∴AC=DB,
∴AC-BC=DB-BC,
即AB=CD.
∵AD=11,BC=4,
∴AB=(AD-BC)=×(11-4)=3.5,
即AB=3.5.
变式练2 解:∵△ACF≌△ADE,
∴AE=AF,AD=AC,
∴AD-AF=AD-AE,
∴DF=AD-AF=AD-AE=9-4=5.
母题3 证明:∵△ABC≌△DEF,
∴∠A=∠D,∠ACB=∠DFE,
∴∠BCF=∠EFA,
∴EF∥CB.
∵∠D=∠A,
∴ED∥AB.
变式练3 证明:∵△ABE≌△DCE,
∴∠A=∠ADC.
∵∠F=∠A,
∴∠F=∠ADC,
∴AD∥BF.
母题4 解:AC⊥FE.
证明:如题图2,由题意知,Rt△ABC≌Rt△CDE,
∴∠BAC=∠DCE.
在Rt△ABC中,∵∠BAC+∠ACB=90°,
∴∠DCE+∠ACB=90°,
∴∠ACE=180°-(∠DCE+∠ACB)=180°-90°=90°,∴AC⊥FE.
变式练4 解:成立,证明略.
母题5 解:∵直角△ABC沿BC方向平移得到直角△DEF,
∴DE=AB=8.
∵DM=5,
∴ME=DE-DM=8-5=3.
由平移可得
S阴影=S△DEF-S△MEC
=S△ABC-S△MEC
=S梯形ABEM
=×(3+8)×8,
=44.
变式练5 解:(1)∵将△ABC沿BC方向平移到△DEF的位置,
∴△ABC≌△DEF,
∴AB=DE=5,∠DEF=∠B=85°,
∠D=∠A=60°,
∴∠F=180°-∠D-∠DEF=35°.
∵EH=3,∴DH=DE-EH=2.
(2)证明:∵△ABC≌△DEF,
∴∠ACB=∠F,
∴AC∥DF.
母题6 A 提示:由旋转的性质可知,△ABC≌△ADE,
∴DE=BC,∠BAC=∠DAE,
∴∠CAE=∠CAB-∠BAE,∠DAB=∠DAE-∠BAE,
∴∠EAC=∠DAB.
∵AE=AC,
∴∠AEC=∠C.
∵∠C=∠AED,
∴∠AEC=∠AED,
∴EA平分∠DEC.
∵DE∥AC,
∴∠C=∠BED.
∵∠AEC=∠AED=∠C,
∴∠DEB=60°.
故选A.
变式练6 180° 提示:如图所示.
由图形可得∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°.
∵三个三角形全等,
∴∠4+∠9+∠6=180°.
又∵∠5+∠7+∠8=180°.
∴∠1+∠2+∠3+180°+180°=540°,
∴∠1+∠2+∠3的度数是180°.
母题7 D 提示:∵将长方形ABCD沿AE折叠,使点D落在BC边上的点F处,
∴∠DAE=∠EAF.
∵∠BAF=60°,
∴∠DAE=∠EAF=∠DAF=×(90°-60°)=15°.
故选D.
变式练7 B 提示:∵折叠后这个三角形的顶点C落在AB边上的点E处,
∴DE=CD,BE=BC=7 cm,
∴AE=AB-BE=10-7=3(cm).
∵AD+DE=AD+CD=AC=6 cm,
∴△AED的周长=6+3=9(cm).
故选B.
