12.2 三角形全等的判定 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 12.2 三角形全等的判定 重难点突破 任务式练习(含答案) 2024-2025学年数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 329.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-13 00:00:00 | ||
图片预览



文档简介
12.2 三角形全等的判定
任务一 全等三角形的判定与性质的综合应用
子任务1 证明直线的位置关系
母题1 如图,点B,E,C,F在同一直线上,BE=CF,AB=DE,AC=DF.求证:AC∥DF.
【关键点拨】
变式练1:如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一直线上,连接BD.
(1)求证:BD=EC.
(2)BD与CE有何位置关系 请证明你的猜想.
子任务2 证明线段、角相等
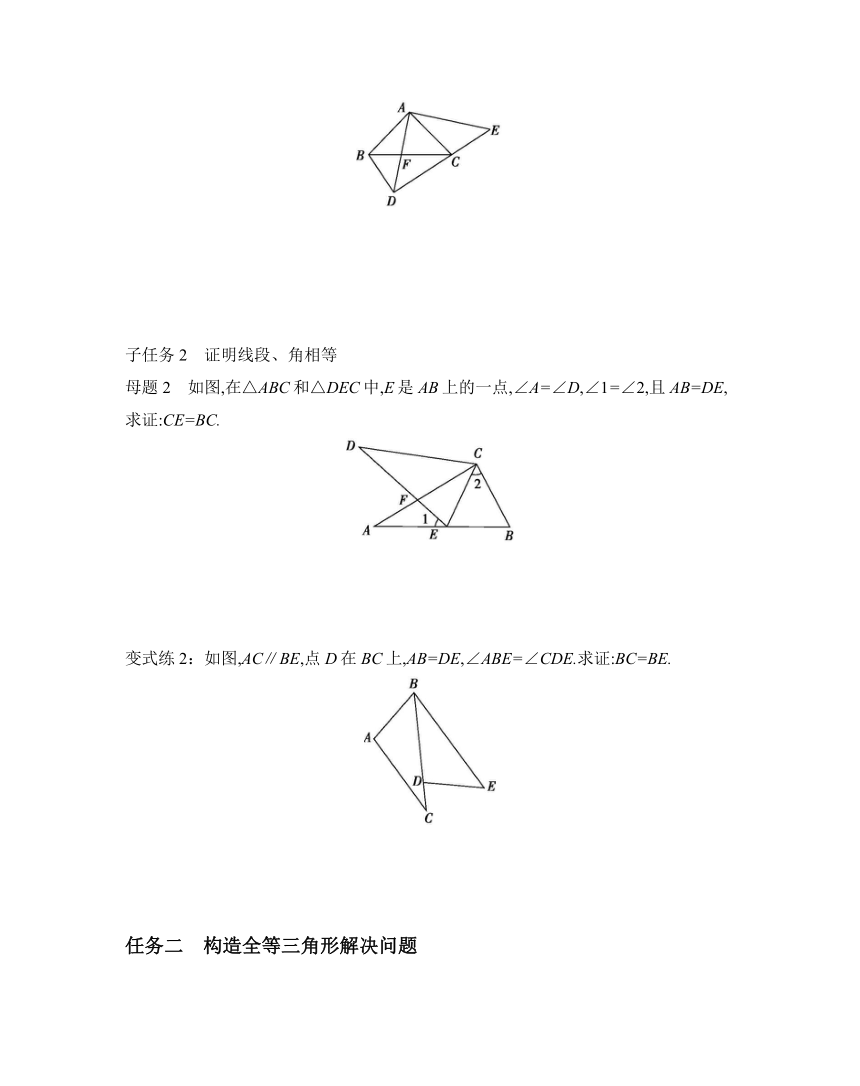
母题2 如图,在△ABC和△DEC中,E是AB上的一点,∠A=∠D,∠1=∠2,且AB=DE,求证:CE=BC.
变式练2:如图,AC∥BE,点D在BC上,AB=DE,∠ABE=∠CDE.求证:BC=BE.
任务二 构造全等三角形解决问题
子任务1 利用倍长中线法构造全等三角形
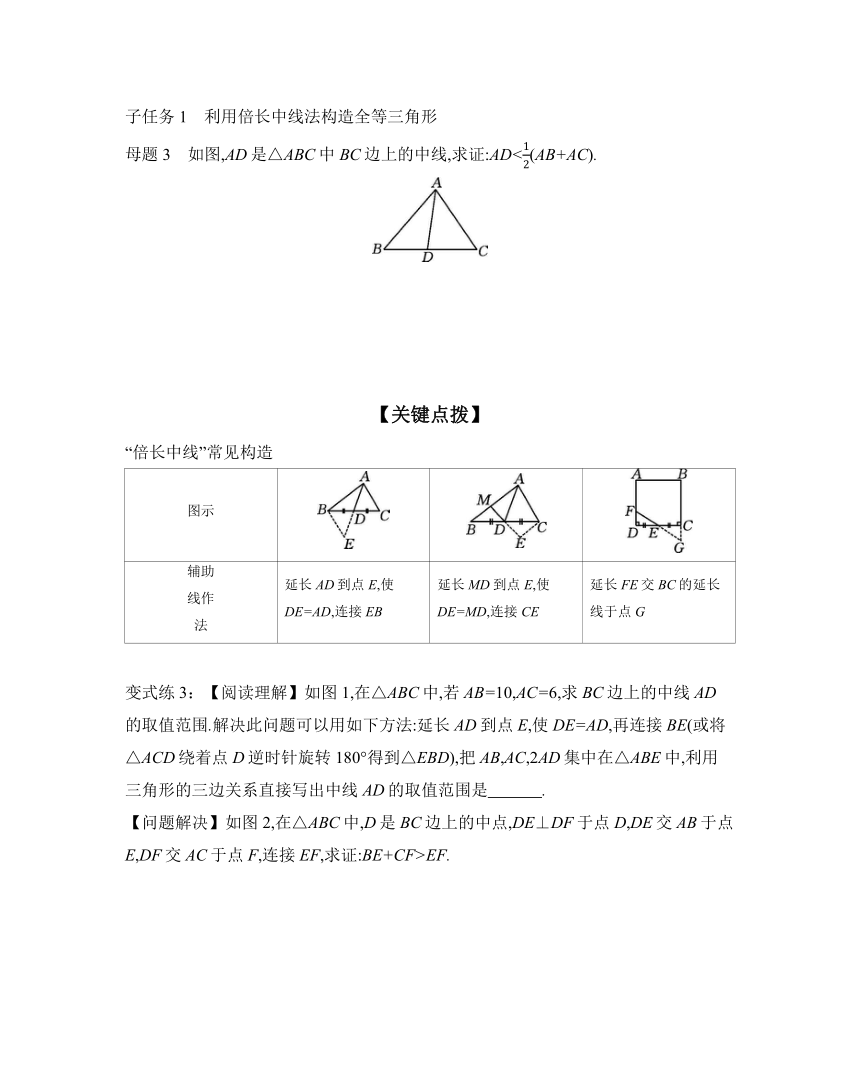
母题3 如图,AD是△ABC中BC边上的中线,求证:AD<(AB+AC).
【关键点拨】
“倍长中线”常见构造
图示
辅助 线作 法 延长AD到点E,使DE=AD,连接EB 延长MD到点E,使DE=MD,连接CE 延长FE交BC的延长线于点G
变式练3:【阅读理解】如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E,使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形的三边关系直接写出中线AD的取值范围是 .
【问题解决】如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF.
子任务2 利用截长补短法构造全等三角形
母题4 如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD
变式练4:如图,在△ABC中,∠B=2∠C,AD是BC边上的高.求证:AB+BD=DC.
任务三 全等三角形中的动态探究题
子任务1 探究直线的运动问题
母题5 在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于点D,CE⊥AE于点E.
(1)如图1,点B,C在AE的同侧,试说明:BD+CE=DE.
(2)若直线AE绕点A旋转,使点B,C在AE的两侧,如图2,图3,则BD,DE与CE的关系如何 请分别写出结论.
【关键点拨】
变式练5:将两个全等的直角三角形ABC和DBE按如图1所示的方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:①CF=EF;②AF+EF=DE.
(2)若将图1中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其他条件不变,如图2.请你直接判断(1)中的两个结论是否成立.
(3)若将图1中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其他条件不变,如图3.请你写出此时AF、EF与DE之间的关系,并加以证明.
子任务2 探究点的运动问题
母题6 在Rt△ABC中,∠C=90°,AC=10 cm,BC=5 cm,P,Q两点分别在AC上和过点A且垂直于AC的射线AM上运动,且PQ=AB,问P点运动到AC上什么位置时,△ABC才能和△QPA全等.
【关键点拨】
变式练6:如图,在正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过多少秒后,△BPE≌△CQP.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等
子任务3 探究图形的平移问题
母题7 如图1,点A,E,F,C在同一条直线上,且AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,垂足分别为E,F,AB=CD.
(1)若EF与BD相交于点G,则EG与FG相等吗 请说明理由.
(2)若将图1中的△DEC沿AC移动到如图2所示的位置,其余条件不变,则(1)中的结论是否仍成立 不必说明理由.
变式练7:如图1,AB⊥BD,DE⊥BD,点C是BD上一点,且BC=DE,CD=AB.
(1)试判断AC与CE的位置关系,并说明理由.
(2)如图2,若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时AC与BE互相垂直吗 请说明理由.
参考答案
母题1 证明:∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS),∴∠ACB=∠F,∴AC∥DF.
变式练1 解:(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴BD=EC.
(2)BD⊥CE.
证明:∵△ABD≌△ACE.
∴∠BDA=∠E.
又∵∠E+∠ADE=90°,
∴∠BDA+∠ADE=90°,即∠BDE=90°,
∴BD⊥CE.
母题2 证明:∵∠2+∠CEB+∠B=180°,∠1+∠CED+∠CEB=180°,∠1=∠2,
∴∠CED=∠B.
在△ABC与△DEC中,
∴△ABC≌△DEC(ASA),
∴CE=BC.
变式练2 证明:∵AC∥BE,∴∠DBE=∠C.
∵∠CDE=∠DBE+∠E,∠ABE=∠ABC+∠DBE,∠ABE=∠CDE,
∴∠E=∠ABC.
在△ABC与△DEB中,
∴△ABC≌△DEB(AAS),
∴BC=BE.
母题3 证明:如图,延长AD至点E,使DE=AD,连接BE.
∵AD是△ABC中BC边上的中线,
∴DC=DB.
在△ACD和△EBD中,
∴△ACD≌△EBD(SAS),
∴AC=BE.
在△ABE中,由三角形的三边关系可得AE∴AD<(AB+AC).
变式练3 解:【阅读理解】2∵AD是BC边上的中线,
∴BD=CD,
在△BDE和△CDA中,
∴△BDE≌△CDA(SAS),
∴BE=AC=6.
在△ABE中,由三角形的三边关系得AB-BE∴10-6∴2【问题解决】证明:如图2,延长FD至点M,使DM=DF,连接BM、EM,
同(1)得△BMD≌△CFD(SAS),
∴BM=CF.
∵DE⊥DF,DM=DF,
∴EM=EF.
在△BME中,由三角形的三边关系得BE+BM>EM,
∴BE+CF>EF.
母题4 证明:如图,在AB上取一点F,使AF=AC,连接EF.
∵EA和EB分别平分∠CAB和∠DBA,
∴∠CAE=∠FAE,∠EBF=∠EBD.
∵AC∥BD,
∴∠C+∠D=180°.
在△ACE和△AFE中,
∴△ACE≌△AFE(SAS),
∴∠C=∠AFE.
∵∠AFE+∠EFB=180°,
∴∠EFB=∠D.
在△BEF和△BED中,
∴△BEF≌△BED(AAS),
∴BF=BD.
∵AB=AF+BF,
∴AB=AC+BD.
变式练4 证明:如图,在线段DC上取一点E,使DE=DB,连接AE,
易证△ABD≌△AED,
∴AB=AE,
∴∠AEB=∠B.
∵∠B=2∠C,
∴∠AEB=2∠C,
∴∠EAC=∠AEB-∠C=2∠C-∠C=∠C,
∴AE=CE,
∴CE=AE=AB,
∴DC=DE+CE=AB+BD,
∴AB+BD=DC.
母题5 解:(1)∵CE⊥DE,BD⊥DE,
∴∠CEA=∠BDA=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
又∠DBA+∠BAD=90°,
∴∠CAE=∠ABD.
在△ACE和△BAD中,
∴△ACE≌△BAD(AAS),
∴CE=AD,AE=BD.
∵AE+AD=DE,
∴BD+CE=DE.
(2)在题图2中,BD-CE=DE.理由如下:
∵CE⊥DE,BD⊥DE,
∴∠CEA=∠BDA=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
又∠DBA+∠BAD=90°,
∴∠CAE=∠ABD.
在△ACE和△BAD中,
∴△ACE≌△BAD(AAS),
∴CE=AD,AE=BD.
∵AE-AD=DE,
∴BD-CE=DE.
在题图3中,CE-BD=DE.理由如下:
∵CE⊥DE,BD⊥DE,
∴∠CEA=∠BDA=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
又∠DBA+∠BAD=90°,
∴∠CAE=∠ABD.
在△ACE和△BAD中,
∴△ACE≌△BAD(AAS),
∴CE=AD,AE=BD.
∵AD-AE=DE,
∴CE-BD=DE.
变式练5 解:(1)证明:①连接BF(如图1).
∵△ABC≌△DBE,
∴BC=BE,AC=DE.
∵∠ACB=∠DEB=90°,
∴∠BCF=∠BEF=90°.
在Rt△BFC和Rt△BFE中,
∴Rt△BFC≌Rt△BFE(HL),
∴CF=EF.
②又∵AF+CF=AC,
∴AF+EF=AC=DE.
(2)(1)中的两个结论成立,理由如下:
如图2,连接BF.
∵△ABC≌△DBE,
∴BC=BE,∠ACB=∠DEB=90°,
在Rt△BCF和Rt△BEF 中,
∴Rt△BCF≌Rt△BEF(HL),
∴EF=CF,
∴AF+EF=AF+CF=AC=DE.
(3)结论:AF=DE+EF.证明如下:
如图3,连接BF.
∵△ABC≌△DBE,
∴BC=BE.
∵∠ACB=∠DEB=90°,
在 Rt△BCF 和 Rt△BEF 中,
∴Rt△BCF≌Rt△BEF(HL),
∴CF=EF.
∵△ABC≌△DBE,
∴AC=DE,
∴AF=AC+FC=DE+EF.
母题6 解:①当点P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=5 cm.
②当点P运动到与点C重合时,AP=AC.
在Rt△QAP与Rt△BCA中,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=10 cm.
综上所述,当点P运动到AP=BC或点P与点C重合时,△ABC才能和△APQ全等.
变式练6 解:(1)设经过t秒后,△BPE≌△CQP.△BPE≌△CQP,∴BP=CQ,∠B=∠C=90°,PC=BE.
∵正方形ABCD的边长为10厘米,BE=6厘米,
∴BP=BC-CP=CQ=4t=4,∴t=1,
∴经过1秒,△BPE≌△CQP.
(2)∵vP≠vQ,
∴BP≠CQ.
又∵△BPE与△CQP全等,∠B=∠C,则BP=PC,BE=CQ=6厘米,
而BP=4t,CP=10-4t,
∴4t=10-4t,
∴点P,点Q运动的时间t=,
∴vQ=6÷=4.8厘米/秒.
母题7 解:(1)EG=FG,理由如下:
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE.
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°.
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△DEG和△BFG中,
∴△DEG≌△BFG(AAS),
∴EG=FG.
(2)(1)中的结论仍成立.
提示:同(1)得Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△DEG和△BFG中,
∴△DEG≌△BFG(AAS),
∴EG=FG.
变式练7 解:(1)AC⊥CE.
理由:∵AB⊥BD,DE⊥BD,
∴∠B=∠D=90°.
在△ABC和△CDE中,
∴△ABC≌△CDE(SAS),
∴∠A=∠DCE,∠ACB=∠E.
∵∠A+∠ACB=90°,
∴∠DCE+∠ACB=90°.
∵∠DCE+∠ACB+∠ACE=180°,
∴∠ACE=90°,
∴AC⊥CE.
(2)AC⊥BE.
理由:如图,
∵△ABC≌△BDE,
∴∠A=∠EBD,∠ACB=∠E.
∵∠A+∠ACB=90°,
∴∠EBD+∠ACB=90°,
∴∠BFC=90°,
∴AC⊥BE.
任务一 全等三角形的判定与性质的综合应用
子任务1 证明直线的位置关系
母题1 如图,点B,E,C,F在同一直线上,BE=CF,AB=DE,AC=DF.求证:AC∥DF.
【关键点拨】
变式练1:如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一直线上,连接BD.
(1)求证:BD=EC.
(2)BD与CE有何位置关系 请证明你的猜想.
子任务2 证明线段、角相等
母题2 如图,在△ABC和△DEC中,E是AB上的一点,∠A=∠D,∠1=∠2,且AB=DE,求证:CE=BC.
变式练2:如图,AC∥BE,点D在BC上,AB=DE,∠ABE=∠CDE.求证:BC=BE.
任务二 构造全等三角形解决问题
子任务1 利用倍长中线法构造全等三角形
母题3 如图,AD是△ABC中BC边上的中线,求证:AD<(AB+AC).
【关键点拨】
“倍长中线”常见构造
图示
辅助 线作 法 延长AD到点E,使DE=AD,连接EB 延长MD到点E,使DE=MD,连接CE 延长FE交BC的延长线于点G
变式练3:【阅读理解】如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E,使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形的三边关系直接写出中线AD的取值范围是 .
【问题解决】如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF.
子任务2 利用截长补短法构造全等三角形
母题4 如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD
变式练4:如图,在△ABC中,∠B=2∠C,AD是BC边上的高.求证:AB+BD=DC.
任务三 全等三角形中的动态探究题
子任务1 探究直线的运动问题
母题5 在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于点D,CE⊥AE于点E.
(1)如图1,点B,C在AE的同侧,试说明:BD+CE=DE.
(2)若直线AE绕点A旋转,使点B,C在AE的两侧,如图2,图3,则BD,DE与CE的关系如何 请分别写出结论.
【关键点拨】
变式练5:将两个全等的直角三角形ABC和DBE按如图1所示的方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:①CF=EF;②AF+EF=DE.
(2)若将图1中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其他条件不变,如图2.请你直接判断(1)中的两个结论是否成立.
(3)若将图1中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其他条件不变,如图3.请你写出此时AF、EF与DE之间的关系,并加以证明.
子任务2 探究点的运动问题
母题6 在Rt△ABC中,∠C=90°,AC=10 cm,BC=5 cm,P,Q两点分别在AC上和过点A且垂直于AC的射线AM上运动,且PQ=AB,问P点运动到AC上什么位置时,△ABC才能和△QPA全等.
【关键点拨】
变式练6:如图,在正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过多少秒后,△BPE≌△CQP.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等
子任务3 探究图形的平移问题
母题7 如图1,点A,E,F,C在同一条直线上,且AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,垂足分别为E,F,AB=CD.
(1)若EF与BD相交于点G,则EG与FG相等吗 请说明理由.
(2)若将图1中的△DEC沿AC移动到如图2所示的位置,其余条件不变,则(1)中的结论是否仍成立 不必说明理由.
变式练7:如图1,AB⊥BD,DE⊥BD,点C是BD上一点,且BC=DE,CD=AB.
(1)试判断AC与CE的位置关系,并说明理由.
(2)如图2,若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时AC与BE互相垂直吗 请说明理由.
参考答案
母题1 证明:∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS),∴∠ACB=∠F,∴AC∥DF.
变式练1 解:(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴BD=EC.
(2)BD⊥CE.
证明:∵△ABD≌△ACE.
∴∠BDA=∠E.
又∵∠E+∠ADE=90°,
∴∠BDA+∠ADE=90°,即∠BDE=90°,
∴BD⊥CE.
母题2 证明:∵∠2+∠CEB+∠B=180°,∠1+∠CED+∠CEB=180°,∠1=∠2,
∴∠CED=∠B.
在△ABC与△DEC中,
∴△ABC≌△DEC(ASA),
∴CE=BC.
变式练2 证明:∵AC∥BE,∴∠DBE=∠C.
∵∠CDE=∠DBE+∠E,∠ABE=∠ABC+∠DBE,∠ABE=∠CDE,
∴∠E=∠ABC.
在△ABC与△DEB中,
∴△ABC≌△DEB(AAS),
∴BC=BE.
母题3 证明:如图,延长AD至点E,使DE=AD,连接BE.
∵AD是△ABC中BC边上的中线,
∴DC=DB.
在△ACD和△EBD中,
∴△ACD≌△EBD(SAS),
∴AC=BE.
在△ABE中,由三角形的三边关系可得AE
变式练3 解:【阅读理解】2
∴BD=CD,
在△BDE和△CDA中,
∴△BDE≌△CDA(SAS),
∴BE=AC=6.
在△ABE中,由三角形的三边关系得AB-BE
同(1)得△BMD≌△CFD(SAS),
∴BM=CF.
∵DE⊥DF,DM=DF,
∴EM=EF.
在△BME中,由三角形的三边关系得BE+BM>EM,
∴BE+CF>EF.
母题4 证明:如图,在AB上取一点F,使AF=AC,连接EF.
∵EA和EB分别平分∠CAB和∠DBA,
∴∠CAE=∠FAE,∠EBF=∠EBD.
∵AC∥BD,
∴∠C+∠D=180°.
在△ACE和△AFE中,
∴△ACE≌△AFE(SAS),
∴∠C=∠AFE.
∵∠AFE+∠EFB=180°,
∴∠EFB=∠D.
在△BEF和△BED中,
∴△BEF≌△BED(AAS),
∴BF=BD.
∵AB=AF+BF,
∴AB=AC+BD.
变式练4 证明:如图,在线段DC上取一点E,使DE=DB,连接AE,
易证△ABD≌△AED,
∴AB=AE,
∴∠AEB=∠B.
∵∠B=2∠C,
∴∠AEB=2∠C,
∴∠EAC=∠AEB-∠C=2∠C-∠C=∠C,
∴AE=CE,
∴CE=AE=AB,
∴DC=DE+CE=AB+BD,
∴AB+BD=DC.
母题5 解:(1)∵CE⊥DE,BD⊥DE,
∴∠CEA=∠BDA=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
又∠DBA+∠BAD=90°,
∴∠CAE=∠ABD.
在△ACE和△BAD中,
∴△ACE≌△BAD(AAS),
∴CE=AD,AE=BD.
∵AE+AD=DE,
∴BD+CE=DE.
(2)在题图2中,BD-CE=DE.理由如下:
∵CE⊥DE,BD⊥DE,
∴∠CEA=∠BDA=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
又∠DBA+∠BAD=90°,
∴∠CAE=∠ABD.
在△ACE和△BAD中,
∴△ACE≌△BAD(AAS),
∴CE=AD,AE=BD.
∵AE-AD=DE,
∴BD-CE=DE.
在题图3中,CE-BD=DE.理由如下:
∵CE⊥DE,BD⊥DE,
∴∠CEA=∠BDA=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
又∠DBA+∠BAD=90°,
∴∠CAE=∠ABD.
在△ACE和△BAD中,
∴△ACE≌△BAD(AAS),
∴CE=AD,AE=BD.
∵AD-AE=DE,
∴CE-BD=DE.
变式练5 解:(1)证明:①连接BF(如图1).
∵△ABC≌△DBE,
∴BC=BE,AC=DE.
∵∠ACB=∠DEB=90°,
∴∠BCF=∠BEF=90°.
在Rt△BFC和Rt△BFE中,
∴Rt△BFC≌Rt△BFE(HL),
∴CF=EF.
②又∵AF+CF=AC,
∴AF+EF=AC=DE.
(2)(1)中的两个结论成立,理由如下:
如图2,连接BF.
∵△ABC≌△DBE,
∴BC=BE,∠ACB=∠DEB=90°,
在Rt△BCF和Rt△BEF 中,
∴Rt△BCF≌Rt△BEF(HL),
∴EF=CF,
∴AF+EF=AF+CF=AC=DE.
(3)结论:AF=DE+EF.证明如下:
如图3,连接BF.
∵△ABC≌△DBE,
∴BC=BE.
∵∠ACB=∠DEB=90°,
在 Rt△BCF 和 Rt△BEF 中,
∴Rt△BCF≌Rt△BEF(HL),
∴CF=EF.
∵△ABC≌△DBE,
∴AC=DE,
∴AF=AC+FC=DE+EF.
母题6 解:①当点P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=5 cm.
②当点P运动到与点C重合时,AP=AC.
在Rt△QAP与Rt△BCA中,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=10 cm.
综上所述,当点P运动到AP=BC或点P与点C重合时,△ABC才能和△APQ全等.
变式练6 解:(1)设经过t秒后,△BPE≌△CQP.△BPE≌△CQP,∴BP=CQ,∠B=∠C=90°,PC=BE.
∵正方形ABCD的边长为10厘米,BE=6厘米,
∴BP=BC-CP=CQ=4t=4,∴t=1,
∴经过1秒,△BPE≌△CQP.
(2)∵vP≠vQ,
∴BP≠CQ.
又∵△BPE与△CQP全等,∠B=∠C,则BP=PC,BE=CQ=6厘米,
而BP=4t,CP=10-4t,
∴4t=10-4t,
∴点P,点Q运动的时间t=,
∴vQ=6÷=4.8厘米/秒.
母题7 解:(1)EG=FG,理由如下:
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE.
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°.
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△DEG和△BFG中,
∴△DEG≌△BFG(AAS),
∴EG=FG.
(2)(1)中的结论仍成立.
提示:同(1)得Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△DEG和△BFG中,
∴△DEG≌△BFG(AAS),
∴EG=FG.
变式练7 解:(1)AC⊥CE.
理由:∵AB⊥BD,DE⊥BD,
∴∠B=∠D=90°.
在△ABC和△CDE中,
∴△ABC≌△CDE(SAS),
∴∠A=∠DCE,∠ACB=∠E.
∵∠A+∠ACB=90°,
∴∠DCE+∠ACB=90°.
∵∠DCE+∠ACB+∠ACE=180°,
∴∠ACE=90°,
∴AC⊥CE.
(2)AC⊥BE.
理由:如图,
∵△ABC≌△BDE,
∴∠A=∠EBD,∠ACB=∠E.
∵∠A+∠ACB=90°,
∴∠EBD+∠ACB=90°,
∴∠BFC=90°,
∴AC⊥BE.
